PreCalculus Chapter 1 Section 1 2 Modeling with

Pre-Calculus Chapter 1 Section 1 & 2 Modeling with Equations and Solving Functions and Their Properties 2013 - 2014

A pizzeria sells a rectangular 20” by 22” pizza for the same amount as a large round pizza (24” diameter). If both pizzas are the same thickness, which option gives you the most pizza for the money

The engineers at an auto manufacturer pay students $0. 08 per mile plus $25 per day to road test their new vehicles. How much did the auto manufacturer pay Sally to drive 440 miles in one day? John earned $93 test-driving a new car in one day. How far did he drive?

Things you should know about Functions � Domain: � Range: Input values, x, independent Output values, y, dependent � Function: � Vertical Each domain value has 1 y value Line Test: A graph is a function if a vertical line passes through it and only intercepts at 1 point

Find the domain of the functions �

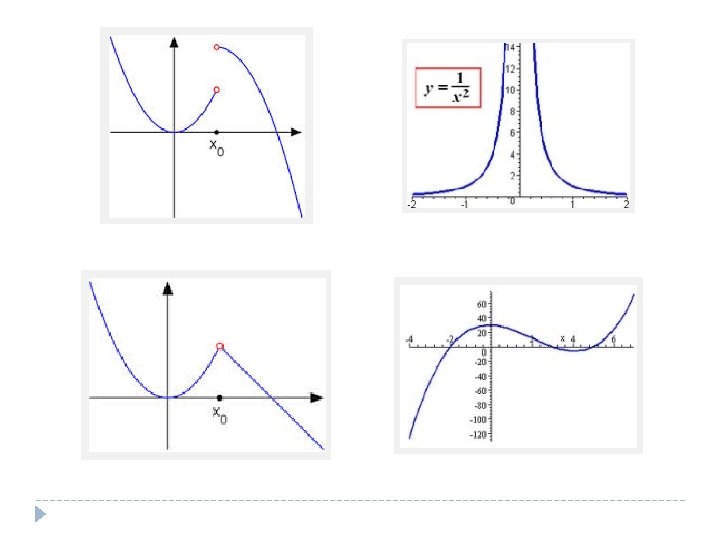
Continuity � Continuous � Removable discontinuity � Jump discontinuity � Infinite discontinuity

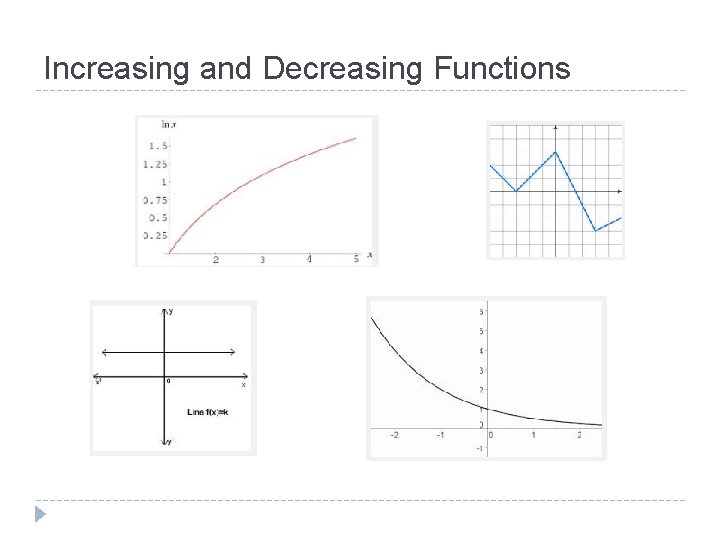
Increasing and Decreasing Functions

For each function, tell the intervals on which it is increasing and decreasing.

Local and Absolute Extrema � Local values are located on an interval. Absolute values are the highest or lowest on the whole graph � Local maximum is the highest point in a section of a graph. If it is actually the highest point, it is the absolute maximum.

Symmetric about the y-axis x y -3 9 -2 4 -1 1 2 4 3 9

Symmetric about the x-axis x y 9 -3 4 -2 1 -1 1 1 4 2 9 3 These are not true functions because they fail the vertical line test. You can say (x, -y) is on the graph when (x, y) is on the graph.

Symmetric about the origin x y -3 -27 -2 -8 -1 -1 1 1 2 8 3 27

Checking symmetry � To check if a function is an even function, subsitute (x) in for x. If the function is the same, it is even. � To check if a function is odd, substitute (-x) in for x. If the function is the opposite sign of the original function, it is odd. � If the rules applied does not fit an even nor odd function, you would say the function is neither.

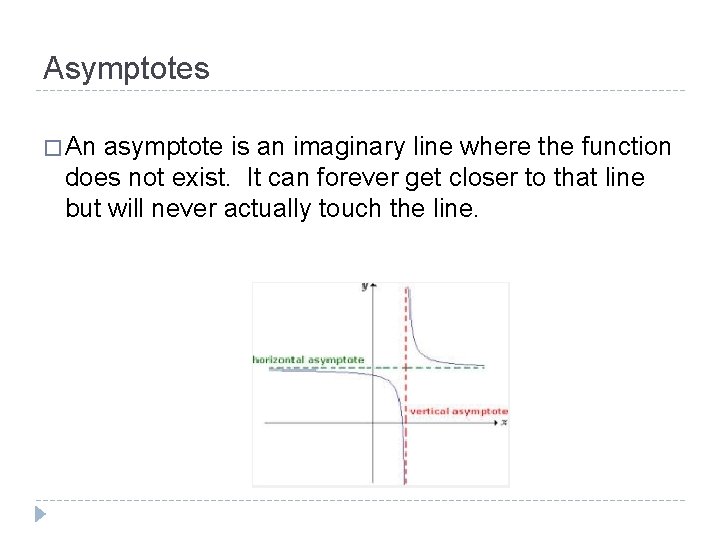
Asymptotes � An asymptote is an imaginary line where the function does not exist. It can forever get closer to that line but will never actually touch the line.

Finding Asymptotes �

Before you leave today: � Complete #79 from page 104

Homework � Ch 1. 1; Pg. 81 -83: 1 -10, 22, 29, 31 � Ch 1. 2; Pg. 102 -103: 1 -25 every other odd, 41 – 61 every other odd, 73