PreCalculus 11 Notes Mr Rodgers Chapter 1 Sequences

Pre-Calculus 11 Notes Mr. Rodgers

Chapter 1 Sequences and Series

Chapter 1. 1 Arithmetic Sequences An arithmetic sequence is an ordered list of terms, where the difference between consecutive terms is constant, or, when the same value or variable is added to each term to create the next term. This constant is called the common difference (d). In order to find the common difference, you subtract the first term from the second term of any two consecutive terms ( ex. d = t 2 - t 1 ). The formula for an arithmetic sequence is: tn = t 1 + (n-1)d where t 1 is the first term of the sequence n is the number of terms d is the common difference tn is the general term or nth term

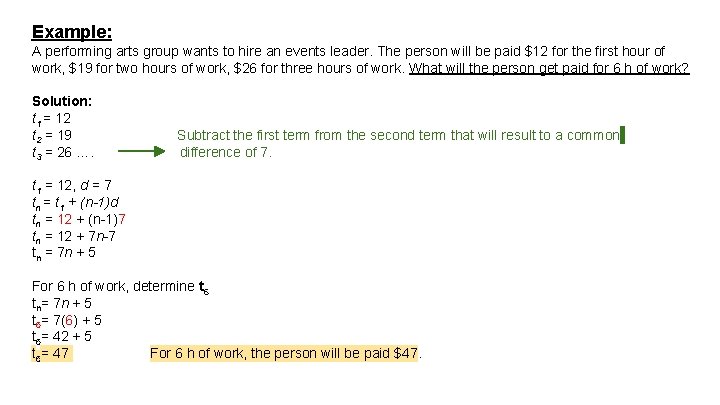
Example: A performing arts group wants to hire an events leader. The person will be paid $12 for the first hour of work, $19 for two hours of work, $26 for three hours of work. What will the person get paid for 6 h of work? Solution: t 1 = 12 t 2 = 19 t 3 = 26 …. Subtract the first term from the second term that will result to a common difference of 7. t 1 = 12, d = 7 tn = t 1 + (n-1)d tn = 12 + (n-1)7 tn = 12 + 7 n-7 tn = 7 n + 5 For 6 h of work, determine t 6 tn= 7 n + 5 t 6= 7(6) + 5 t 6= 42 + 5 t 6= 47 For 6 h of work, the person will be paid $47.

1. 2 Arithmetic Series An arithmetic series are a sum of terms that form an arithmetic sequence. Sn represents the sum of the first n terms of a series. The following is an arithmetic sequence: 1, 3, 5, 7, 9… In this case, S 5 means the sum of the first 5 terms. The formulas are: Sn= n [2 t 1 + (n-1)d] 2 Where t 1 is the first term Sn= n (t 1 + tn) 2 Where t 1 is the first term n is the number of terms d is the common difference tn is the nth term Sn is the sum of the first n terms

Example 1: Find the sum of the first 60 terms of the series 5 + 8 + 11 +. . n = 60, t 1= 5, d = 3 S 60 = 60 (2(5) + 59 (3)) 2 = 30 (10+177) = 30 (187) S 60 = 5610 Example 2: Find the sum of the arithmetic series 5 + 9 + 13 +. . + 201 tn= t 1 + (n-1)d 201 = 5 + (n-1)4 196 = 4(n-1) 49 = n-1 50 = n Sn= n [2 t 1 + (n-1)d] 2 S 50 = 50 (10 + 200) 2 = 25 (210) S 50 = 5250 t 1 = 5, tn= 201, d = 4

1. 3 Geometric Series A geometric sequence is a sequence when the ratio of consecutive terms is constant. The common ratio, r, can be found by taking any term, and dividing that term by the preceding term ( ex. r = t 2 ÷ t 1 ). The formula is: tn = t 1 r n-1 where t 1 is the first term of the sequence n is the number of terms r is the common ratio tn is the general term or nth term - the ratio may be positive or negative for example, in the sequence 2, 4, 8, 16, . . . , the common ratio is 2

Example 1: In the geometric sequence determine the general term tn and the seventh term. 32, 16, 8, … t 1= 32, r = 1 2 7 -1 t 7= 32 (1) 2 t 7= 32 (1) 6 t 7= 32 (1) t 7= 32 t 7= 1 2 64 64 2 Example 2: Bacteria reproduce by dividing in two so that one cell gives rise to 2, then 4, then 8 cells, and so on, producing a geometric sequence. Suppose there were 10 bacteria in a sample. Determine the general term and state the values of t 1 and r. t 1= 10, t 2= 20, t 3= 40 tn = t 1 r n-1 Divide the second term by the first term to find a common ratio of 2. t 1= 10 and r = 2 tn = (10)(2) n-1 The general term of the sequence is tn = 10(2) n-1.

1. 4 Geometric Series A geometric series is the sum of the terms in a geometric sequence. We use the symbol Sn to represent the sum of the first n terms of a geometric sequence. For example, 3 + 6 + 12 + 24 is a geometric series. The formula is: Sn= t 1(r n- 1) , r ≠ 1 r-1 where t 1 is the first term of the series n is the number of terms r is the common ratio Sn is the sum of the first n terms

Example 1: Determine the sum of the first 10 terms of the geometric series. 4 + 12 + 36 + … t 1 = 4, r = 3, n = 10 Sn= t 1(r n- 1) r-1 S 10= 4(310 -1) 3 -1 S 10= 4(59 048) 2 S 10= 118 0964 Example 2: In a geometric sequence, the fifth term is 1024 and the common ratio is 4. Find the sum of the first seven terms of this series. t 5= 1024, r = 4, n = 7 Find Sn tn = t 1 r n-1 1024 = (256)t 1 4 = t 1 Sn= t 1(r n- 1) r-1 divide both sides by 256 S 7 = 4(47 -1) 4 -1 S 7 = 21844

1. 5 Infinite Geometric Series The formula for an infinite geometric series is: S∞ = t 1 1 -r -1 < r < 1 where t 1 is the first term of the series r is the common ratio Sn represents the sum of an infinite number of terms An infinite geometric series can be either convergent or divergent. A convergent series is when the sequence of partial sums approaches a fixed value, or when r is within the range of -1 < r < 1 ( ex. 1 + 0. 5 + 0. 25 + 0. 125 + … ) A divergent series is when the sequence of partial sums does not approach a fixed value, or when r is out of the range of -1 < r < 1. ( ex. 2 + 4 + 8 + 16 + … )

Example: Decide whether each infinite geometric series is convergent or divergent. State the sum of the series if it exists. a) 1 - 1 + 1 - … b) 2 -4+8 -… 3 9 t 1 = 1, r = -1 t 1 = 2, r = -2 3 Since -1 < r < 1, the series is convergent. Since r < - 1, the series is divergent and has no sum. S∞ = t 1 1 -r S∞ = 1 1 - (-1) ( 3) S∞ = 1 (4) (3) S∞ = (1)3 4 S∞ = 3 4