PRAM Model for Parallel Computation Chapter 1 A

PRAM Model for Parallel Computation Chapter 1 A: Part 2 of Chapter 1 1

The RAM Model of Computation Revisited The Random Access Model (or RAM) model for sequential computation was discussed earlier. Assume that the memory has M memory locations, where M is a large (finite) number Accessing memory can be done in unit time. Instructions are executed one after another, with no concurrent operations. The input size depends on the problem being studied and is the number of items in the input The running time of an algorithm is the number of primitive operations or steps performed. 2

PRAM (Parallel Random Access Machine) PRAM is a natural generalization of the RAM sequential model. Each of the p processors P 0, P 1, … , Pp-1 are identical to a RAM processor and are often referred to as processing elements (PEs) or simply as processors. All processors can read or write to a shared global memory in parallel (i. e. , at the same time). The processors can also perform various arithmetic and logical operations in parallel Running time can be measured in terms of the number of parallel memory accesses an algorithm performs. 3

PRAM Properties An unbounded number of processors all can access All processors can access an unbounded shared memory All processor’s execution steps are synchronized However, processors can run different programs. n Each processor has an unique id, called the pid n Processors can be instructed to do different things, based on their pid (if pid < 200, do this, else do that) 4

The PRAM Model Parallel Random Access Machine n n n Theoretical model for parallel machines p processors with uniform access to a large memory bank UMA (uniform memory access) – Equal memory access time for any processor to any address 5

The PRAM Models PRAM models vary according n n How they handle write conflicts The models differ in how fast they can solve various problems. Exclusive Read, Exclusive Write (EREW) n Only one processor is allow to read or write to the same memory cell during any one step Concurrent Read Exclusive Write (CREW) Concurrent Read Concurrent Write (CRCW) n An algorithm that works correctly for EREW will also work correctly for CREW and CRCW, but not vice versa 6

Summary of Memory Protocols Exclusive-Read Exclusive-Write Exclusive-Read Concurrent-Write Concurrent-Read Exclusive-Write Concurrent-Read Concurrent-Write If concurrent write is allowed we must decide which “written value” to accept 7

Assumptions There is no upper bound on the number of processors in the PRAM model. Any memory location is uniformly accessible from any processor. There is no limit on the amount of shared memory in the system. Resource contention is absent. The algorithms designed for the PRAM model can be implemented on real parallel machines, but will incur communication cost. Since communication and resource costs varies on real machines, PRAM algorithms can be used to establish a lower bound on running time for problems. 8

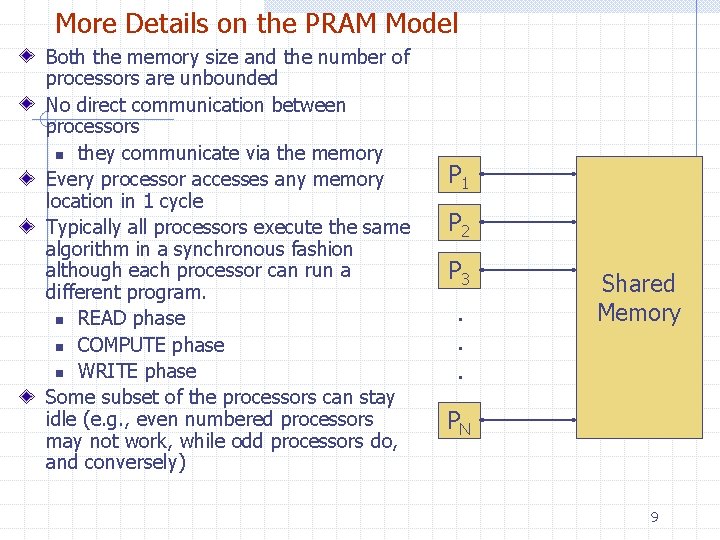
More Details on the PRAM Model Both the memory size and the number of processors are unbounded No direct communication between processors n they communicate via the memory Every processor accesses any memory location in 1 cycle Typically all processors execute the same algorithm in a synchronous fashion although each processor can run a different program. n READ phase n COMPUTE phase n WRITE phase Some subset of the processors can stay idle (e. g. , even numbered processors may not work, while odd processors do, and conversely) P 1 P 2 P 3. . . Shared Memory PN 9

PRAM CW? What ends up being stored when multiple writes occur? n priority CW: processors are assigned priorities and the top priority processor is the one that does writing for each group write n Fail common CW: if values are not equal, no write occurs n Collision common CW: if values not equal, write a “failure value” n Fail-safe common CW: if values not equal, then algorithm aborts n Random CW: non-deterministic choice of which value is written n Combining CW: write the sum, average, max, min, etc. of the values n etc. For CRCW PRAM, one of the above type CWs is assumed. The CWs can be ordered so that later type CWs can execute the earlier types of CWs. As shown in the textbook, Parallel Computation: Models & Algorithms” by Selim Akl, a PRAM machine that can perform all of PRAM operations including all CWs can be built with circuits and runs in O(log n) time. In fact, most PRAM algorithms end up not needing CW. 10

PRAM Example 1 Problem: n We have a linked list of length n n For each element i, compute its distance to the end of the list: d[i] = 0 if next[i] = NIL d[i] = d[next[i]] + 1 otherwise Sequential algorithm is O(n) We can define a PRAM algorithm running in O(log n) time n Associate one processor to each element of the list n At each iteration split the list in two with odd-placed and even-placed elements in different lists n List size is divided by 2 at each step, hence O(log n) 11

End of Current Coverage Some of the remaining slides may be covered at a later date 12

PRAM Example 1 Principle: Look at the next element Add its d[i] value to yours Point to the next element’s next element 1 1 1 0 2 2 1 0 4 4 3 2 1 0 5 4 3 2 1 0 The active processors in each list is reduced by 2 at each step, hence the O(log n) complexity 13

PRAM Example 1 Algorithm forall i if next[i] == NIL then d[i] 0 else d[i] 1 while there is an i such that next[i] ≠ NIL forall i if next[i] ≠ NIL then d[i] + d[next[i]] next[i]] What about the correctness of this algorithm? 14

forall Loop At each step, the updates must be synchronized so that pointers point to the right things: next[i]] Ensured by the semantic of forall i A[i] = B[i] forall i tmp[i] = B[i] forall i A[i] = tmp[i] Nobody really writes it out, but one mustn’t forget that it’s really what happens underneath 15

while Condition while there is an i such that next[i] ≠NULL How can one do such a global test on a PRAM? n Cannot be done in constant time unless the PRAM is CRCW w At the end of above step, each processor could write to a same memory location TRUE or FALSE depending on next[i] being equal to NULL or not, and one can then take the AND of all values (to resolve concurrent writes) w On a PRAM CREW, one needs O(log n) steps for doing a global test like the above In this case, one can just rewrite the while loop into a for loop, because we have analyzed the way in which the iterations go: for step = 1 to log n 16

What Type of PRAM? The previous algorithm does not require a CW machine, but: tmp[i] d[i] + d[next[i] could require a concurrent reads by proc j and k if k=next[j] and k performed the “d[i]” part of execution while j performed the “d[next[i]]” part of this execution Solution 1: Won’t occur if inline execution is strictly synchronous as d[k] and d[next[j]] will execute at different times Solution 2: Execute two inline instructions on lines: tmp 2[i] d[i] tmp[i] tmp 2[i] + d[next[i]] (note that the above are technically in two different steps in each pass through this loop) Now we have an execution that works on a EREW PRAM, 17 which is the most restrictive type

Final Algorithm on a EREW PRAM forall i if next[i] == NILL then d[i] 0 else d[i] 1 for step = 1 to log n forall i if next[i] ≠ NIL then tmp[i] d[i] tmp[i] + d[next[i]] O(1) next[i]] O(1) O(log n) Conclusion: One can compute the length of a list of size n in time O(log n) on any PRAM 18

Are All PRAMs Equivalent? Consider the following problem n Given an array of n elements, ei=1, n, all distinct, find whether some element e is in the array On a CREW PRAM, there is an algorithm that works in time O(1) on n processors: n n n P 1 initializes a boolean variable B to FALSE Each processor i reads ei and e and compare them If equal, then processor Pi writes TRUE into a boolean memory location B. w Only one Pi will write since ei elements are unique , so we’re ok for CREW 19

Are All PRAMs Equivalent? On a EREW PRAM, one cannot do better than log n running time: n n Each processor must read e separately At worst a complexity of O(n), with sequential reads At best a complexity of O(log n), with series of “doubling” of the value at each step so that eventually everybody has a copy (just like a broadcast in a binary tree, or in fact a k-ary tree for some constant k) Generally, “diffusion of information” to n processors on an EREW PRAM takes O(log n) Conclusion: CREW PRAMs are more powerful 20 than EREW PRAMs

This is a Typical Question for Various Parallel Models Is model A more powerful than model B? Basically, you are asking if one can simulate the other. Whether or not the model maps to a “real” machine, is another question of interest. Often a research group tries to build a machine that has the characteristics of a given model. 21

Simulation Theorem Simulation theorem: Any algorithm running on a CRCW PRAM with p processors cannot be more than O(log p) times faster than the best algorithm on a EREW PRAM with p processors for the same problem Proof: We will “simulate” concurrent writes. Let ti denote ti t. w When Pi writes value xi to address li, one replaces the write by an (exclusive) write of (li , xi) to A[i], where A[i] is an auxiliary array with one slot per processor w Then one sorts array A by the first component of its content w Processor i of the EREW PRAM looks at A[i] and A[i-1] n If the first two components are different or if i = 0, write value xi to address li w Since A is sorted according to the first component, writing is exclusive 22

Proof (continued) Picking one processor for each competing write P 0 12 8 P 1 P 2 43 29 P 3 P 4 P 5 26 92 P 0 (29, 43) = A[0]=(8, 12) P 0 writes P 1 (8, 12) = A[1]=(8, 12) P 1 nothing P 2 (29, 43) = A[2]=(29, 43) P 2 writes P 3 (29, 43) = A[3]=(29, 43) P 3 nothing P 4 (92, 26) = A[4]=(29, 43) P 4 nothing P 5 (8, 12) = A[5]=(92, 26) P 5 writes sort 23

Proof (continued) Note that we said that we just sort array A If we have an algorithm that sorts p elements with O(p) processors in O(log p) time, we’re set Turns out, there is such an algorithm: Cole’s Algorithm. n n n Basically a merge-sort in which lists are merged in constant time! It’s beautiful, but we don’t really have time for it, and it’s rather complicated The complexity constant is quite large, so algorithm is currently not practical. Therefore, the proof is complete. 24

Brent’s Theorem: If a p-processor PRAM algorithm runs in time t, then for any p’<p, there is a p’-processor PRAM algorithm A’ for the same problem that runs in time O(pt/p’) Let the time steps of the algorithm A be numbered 1, 2, …, t. n n Each of these steps requires O(1) time in Algorithm A Steps inside of loops will be listed in order multiple times, and depends on the data size. Algorithm A’ completes the execution of each step, before going on to the next one. n n The p tasks performed by the p processors in each step are divided among the p’ processors, with each performing p/p’ steps. Since processors have same speed, this takes O( p/p’ ) time There are t steps in A, so the entire simulation takes O( p/p’ t) = O(pt/p’) time. 25