Praktikum 12 Integrasi Numerik Tujuan Mahasiswa mampu memahami



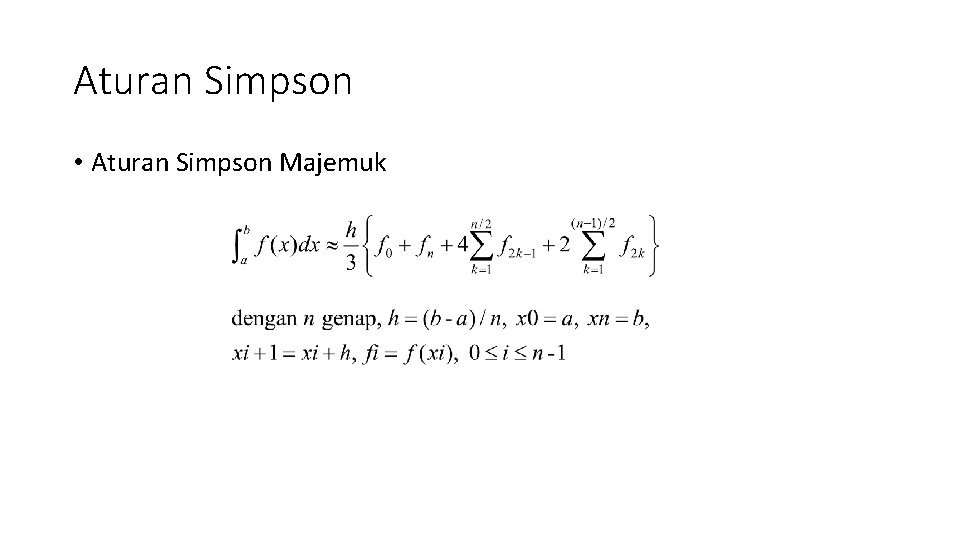
![Contoh • Dengan menggunakan aturan Simpson, hampiri integral fungsi f(x)=1/x pada [1, 9] dengan Contoh • Dengan menggunakan aturan Simpson, hampiri integral fungsi f(x)=1/x pada [1, 9] dengan](https://slidetodoc.com/presentation_image_h/0fee884469dd4d70dd000c607d3914db/image-5.jpg)
![Numerik function hasil=simpmaj(f, x 0, x 1, n) h=(x 1 -x 0)/n; hasil=[]; c=abs((x Numerik function hasil=simpmaj(f, x 0, x 1, n) h=(x 1 -x 0)/n; hasil=[]; c=abs((x](https://slidetodoc.com/presentation_image_h/0fee884469dd4d70dd000c607d3914db/image-6.jpg)





![Dalam Scilab deff('y=f(x)', 'y=x^(-1)') T=[]; I = log(5); for n=0: 5 Tn=traperekursif(f, n, 1, Dalam Scilab deff('y=f(x)', 'y=x^(-1)') T=[]; I = log(5); for n=0: 5 Tn=traperekursif(f, n, 1,](https://slidetodoc.com/presentation_image_h/0fee884469dd4d70dd000c607d3914db/image-12.jpg)




![Dalam Scilab deff('y=f(x)', 'y=(x. ^2+x+1). *cos(x)') T=[]; for n=0: 5, Tn=traperekursif(f, n, 0, %pi/2); Dalam Scilab deff('y=f(x)', 'y=(x. ^2+x+1). *cos(x)') T=[]; for n=0: 5, Tn=traperekursif(f, n, 0, %pi/2);](https://slidetodoc.com/presentation_image_h/0fee884469dd4d70dd000c607d3914db/image-17.jpg)

- Slides: 18

Praktikum 12 Integrasi Numerik

Tujuan • Mahasiswa mampu memahami integrasi numerik dengan menggunakan beberapa metode. • Mahasiswa mampu membedakan metode yang satu dengan yang lainnya • Mahasiswa bisa mengembangkan atau memodifikasi programnya sesuai dengan metode. • Mahasiswa bisa mengimplementasikan aplikasi program kedalam Scilab.

Ruang lingkup bahasan ØKuadratur ØAturan Trapesium ØAturan Simpson ØIntegrasi Romberg
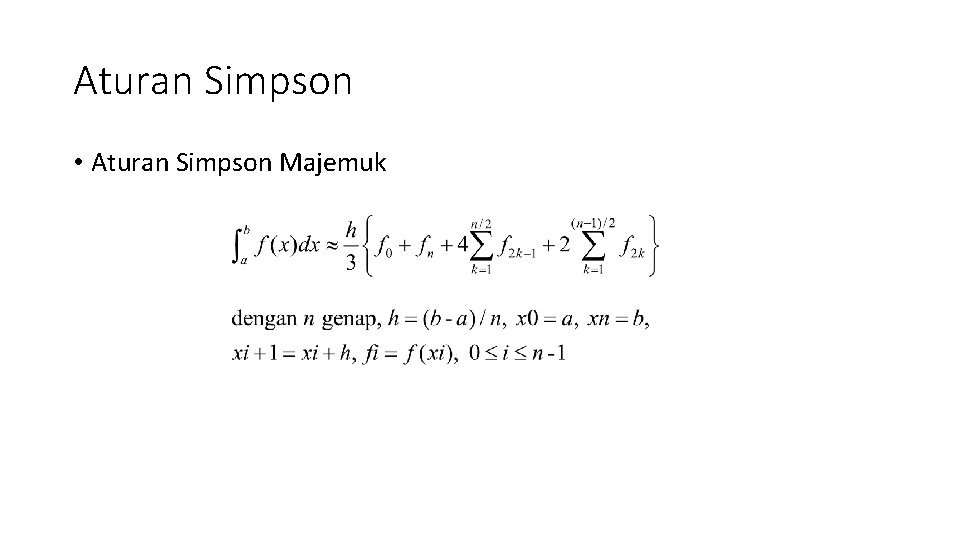
Aturan Simpson • Aturan Simpson Majemuk
![Contoh Dengan menggunakan aturan Simpson hampiri integral fungsi fx1x pada 1 9 dengan Contoh • Dengan menggunakan aturan Simpson, hampiri integral fungsi f(x)=1/x pada [1, 9] dengan](https://slidetodoc.com/presentation_image_h/0fee884469dd4d70dd000c607d3914db/image-5.jpg)
Contoh • Dengan menggunakan aturan Simpson, hampiri integral fungsi f(x)=1/x pada [1, 9] dengan delapan subinterval seragam. • Jawab :
![Numerik function hasilsimpmajf x 0 x 1 n hx 1 x 0n hasil cabsx Numerik function hasil=simpmaj(f, x 0, x 1, n) h=(x 1 -x 0)/n; hasil=[]; c=abs((x](https://slidetodoc.com/presentation_image_h/0fee884469dd4d70dd000c607d3914db/image-6.jpg)
Numerik function hasil=simpmaj(f, x 0, x 1, n) h=(x 1 -x 0)/n; hasil=[]; c=abs((x 1 -x 0)/n); x=x 0: c: x 1; a=f(x 0); b=f(x 1); c=0; d=0; for i=1: n/2, d=d+4*(f(2*i)); end for i=2: n/2, c=c+2*(f(2*i-1)); end hasil=(a+b+c+d)*h/3

Integrasi Romberg • Aturan rekursif trapesium • Misalkan f suatu fungsi yang terdefinisi pada [a, b] dan h=(b-a). Untuk n=1, 2, 4, 8, … atau n=20, 21, 22, 23, …, kita definisikan barisan aturan trapesium dengan Barisan aturan trapesium tersebut memenuhi hubungan

Integrasi Romberg • Dalam menghitung hampiran suatu integral dengan menggunakan aturan trapesium rekursif, kita lakukan langkah sebagai berikut.

Secara numerik • M-file function Tn=traperekursif(f, n, a, b) h=b-a; if n==0, Tn=h*(f(a)+f(b))/2; else if n>0 index=[1: 2: 2^n-1]; x=a+h*index/(2^n); F=f(x); Jf=sum(F); Tn=traperekursif(f, n-1, a, b)/2+Jf*h/(2^n); end

Integrasi Romberg • Aturan rekursif simpson • Misalkan {Tn; n=0, 1, 2, …} adalah barisan aturan trapesium majemuk dan Sn adalah aturan simpson majemuk untuk fungsi f dengan 2 n subinterval pada interval [a, b]. Hubungan antara aturan simpson dangan aturan trapesium majemuk adalah • Aturan rekursif boole • Misalkan {Sn; n=0, 1, 2, …} adalah barisan aturan simpson majemuk dan Bn adalah aturan boole majemuk untuk fungsi f dengan 2 n subinterval pada interval [a, b]. Hubungan antara aturan boole dangan aturan simpson majemuk adalah

Contoh • Hitunglah hampiran integral dengan menggunakan aturan trapesium, simpson, dan boole rekursif dengan cacah interval 1, 2, 3, 4, dan 5. hitunglah pula galat masing-masing hampiran. •
![Dalam Scilab deffyfx yx1 T I log5 for n0 5 Tntraperekursiff n 1 Dalam Scilab deff('y=f(x)', 'y=x^(-1)') T=[]; I = log(5); for n=0: 5 Tn=traperekursif(f, n, 1,](https://slidetodoc.com/presentation_image_h/0fee884469dd4d70dd000c607d3914db/image-12.jpg)
Dalam Scilab deff('y=f(x)', 'y=x^(-1)') T=[]; I = log(5); for n=0: 5 Tn=traperekursif(f, n, 1, 5); T=[T; Tn Tn-I]; end T S=(4*T(2: 6, 1)-T(1: 5, 1))/3; [S S-I] B=(16*S(2: 5)-S(1: 4))/15; [B B-I]

Integrasi Romberg • Metode Romberg Integrasi Romberg dengan ekstrapolasi Richardson

Integrasi Romberg

Contoh • Dengan menggunakan metode Romberg carilah hampiran integral tentu

Contoh • Secara analitik
![Dalam Scilab deffyfx yx 2x1 cosx T for n0 5 Tntraperekursiff n 0 pi2 Dalam Scilab deff('y=f(x)', 'y=(x. ^2+x+1). *cos(x)') T=[]; for n=0: 5, Tn=traperekursif(f, n, 0, %pi/2);](https://slidetodoc.com/presentation_image_h/0fee884469dd4d70dd000c607d3914db/image-17.jpg)
Dalam Scilab deff('y=f(x)', 'y=(x. ^2+x+1). *cos(x)') T=[]; for n=0: 5, Tn=traperekursif(f, n, 0, %pi/2); T=[T; Tn]; end i=[2: 6]'; S(i)=(4*T(i, 1)-T(i-1, 1))/3; i=[3: 6]'; B(i)=(16*S(i)-S(i-1))/15; i=[4: 6]'; R 4(i)=(64*B(i)-B(i-1))/63; i=[5: 6]'; R 5(i)=(256*R 4(i)-R 4(i-1))/255; R 6(6)=(4^5*R 5(6)-R 5(5))/(4^5 -1); [T S B R 4 R 5 R 6]

THE END