Practice Test Unit 3 Geometry Saturday January 8



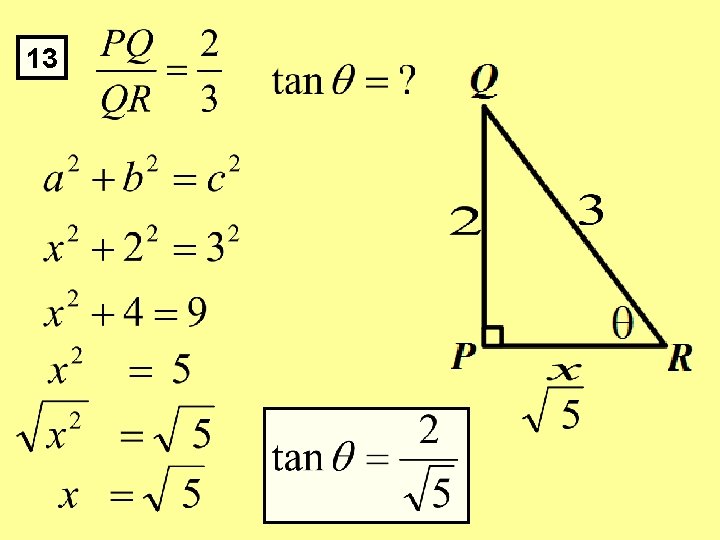













- Slides: 61

Practice Test Unit 3 Geometry Saturday, January 8, 2022

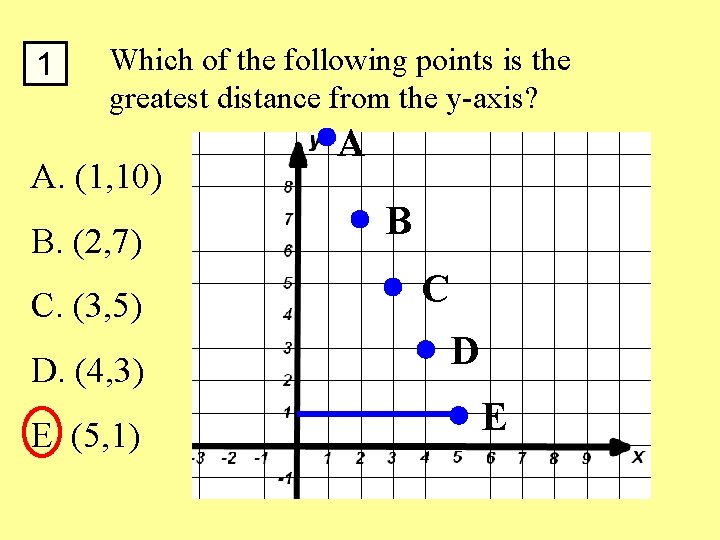
1 Which of the following points is the greatest distance from the y-axis? A. (1, 10) B. (2, 7) C. (3, 5) D. (4, 3) E. (5, 1) A B C D E

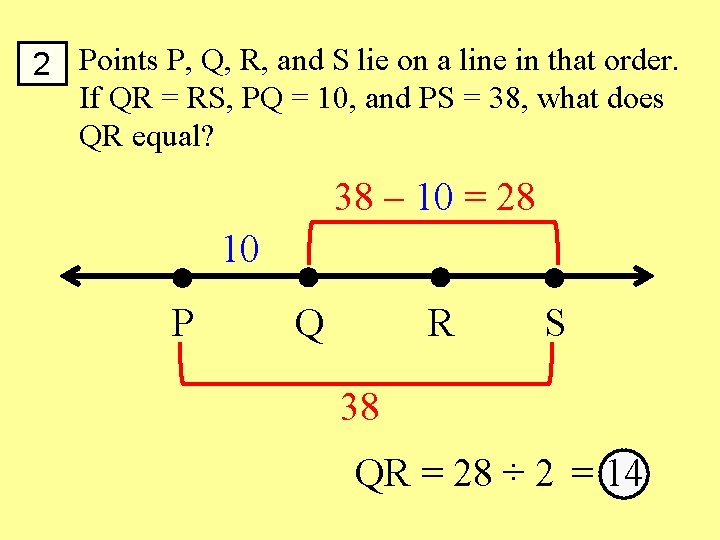
2 Points P, Q, R, and S lie on a line in that order. If QR = RS, PQ = 10, and PS = 38, what does QR equal? 38 – 10 = 28 P 10 Q R S 38 QR = 28 ÷ 2 = 14

3 Find the midpoint between the points (3, – 6) and (7, 13).

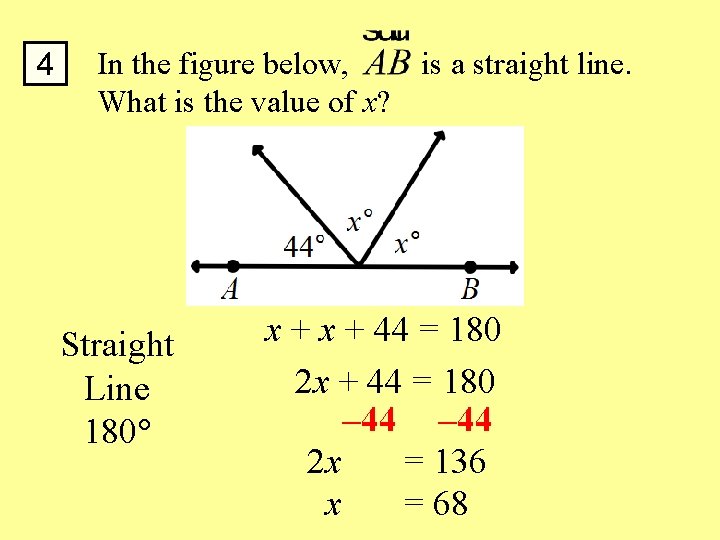
4 In the figure below, is a straight line. What is the value of x? Straight Line 180 x + 44 = 180 2 x + 44 = 180 – 44 2 x = 136 x = 68

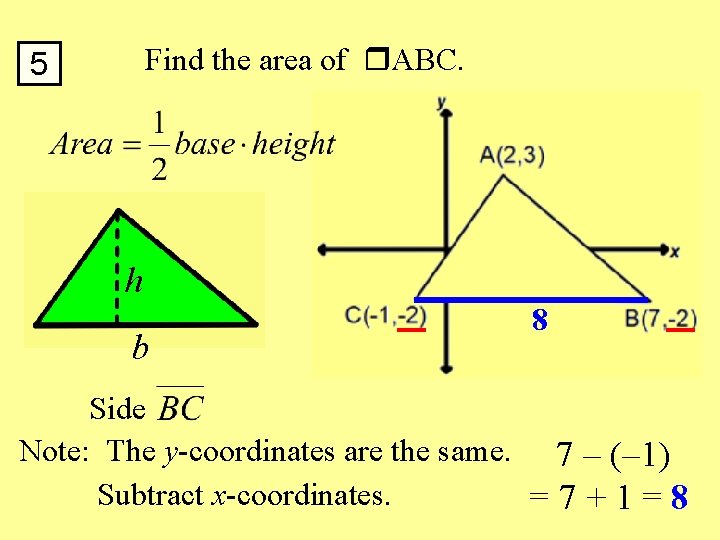
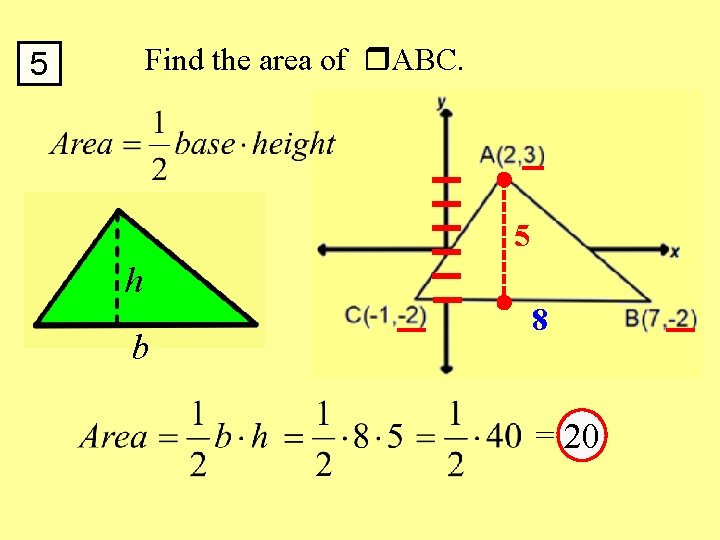
Find the area of ABC. 5 h b 8 Side Note: The y-coordinates are the same. 7 – (– 1) Subtract x-coordinates. =7+1=8

Find the area of ABC. 5 5 h b 8 = 20

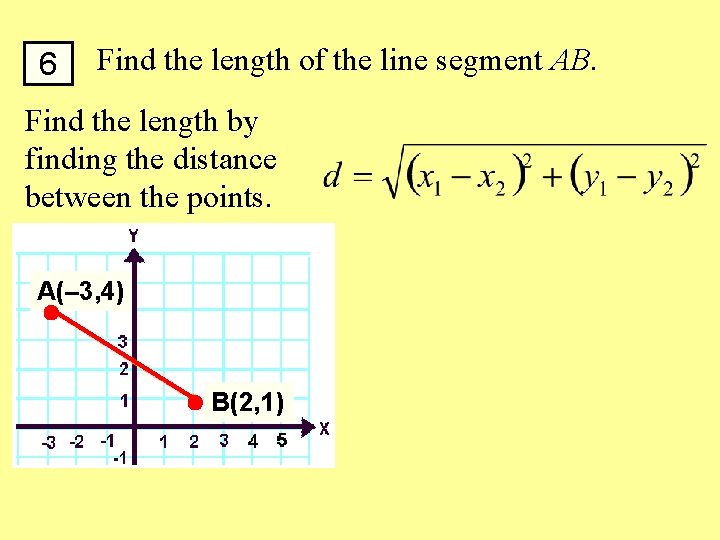
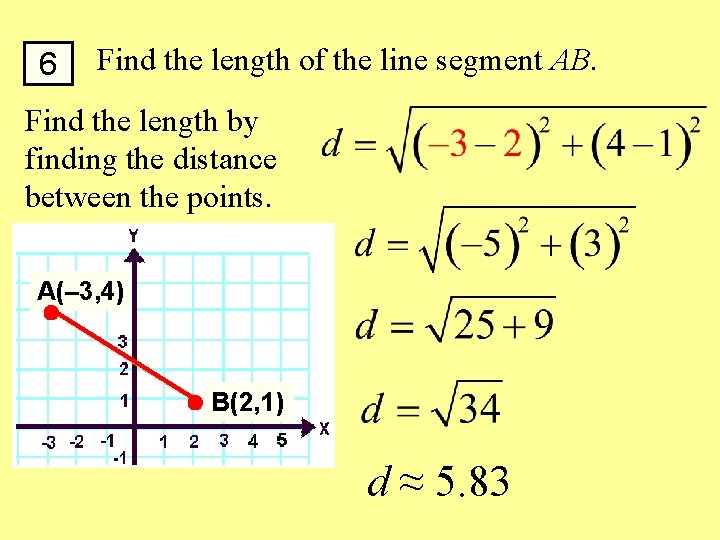
6 Find the length of the line segment AB. Find the length by finding the distance between the points. A(– 3, 4) B(2, 1)

6 Find the length of the line segment AB. Find the length by finding the distance between the points. A(– 3, 4) B(2, 1) d ≈ 5. 83

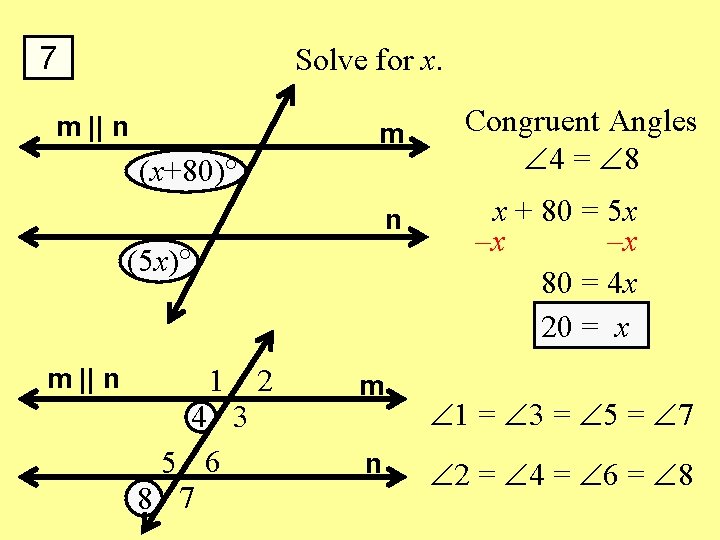
7 Solve for x. m || n m (x+80) n (5 x) m || n 1 4 3 5 6 8 7 2 m n Congruent Angles 4 = 8 x + 80 = 5 x –x –x 80 = 4 x 20 = x 1 = 3 = 5 = 7 2 = 4 = 6 = 8

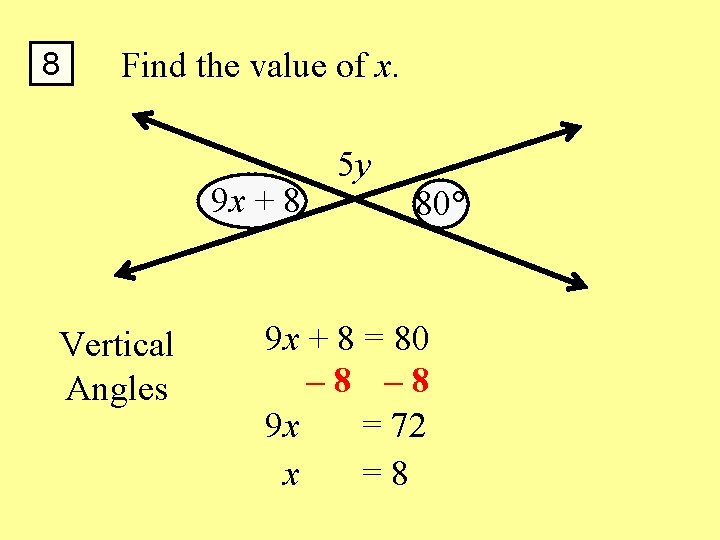
8 Find the value of x. 9 x + 8 Vertical Angles 5 y 80 9 x + 8 = 80 – 8 9 x = 72 x =8

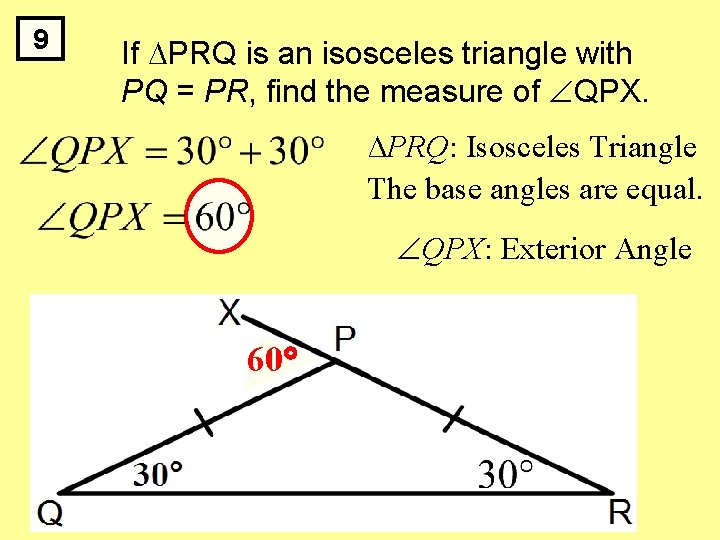
9 If PRQ is an isosceles triangle with PQ = PR, find the measure of QPX. ∆PRQ: Isosceles Triangle The base angles are equal. QPX: Exterior Angle ? 60

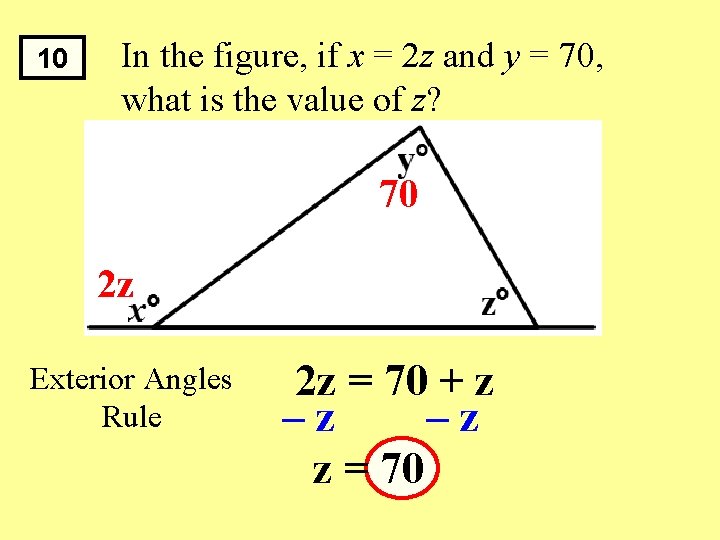
10 In the figure, if x = 2 z and y = 70, what is the value of z? 70 2 z Exterior Angles Rule 2 z = 70 + z –z –z z = 70

11 If the ratio of the angles of a triangle is 2: 3: 4, what is the degree measure of the largest angle? Largest Angle 4 x 4(20) = 80

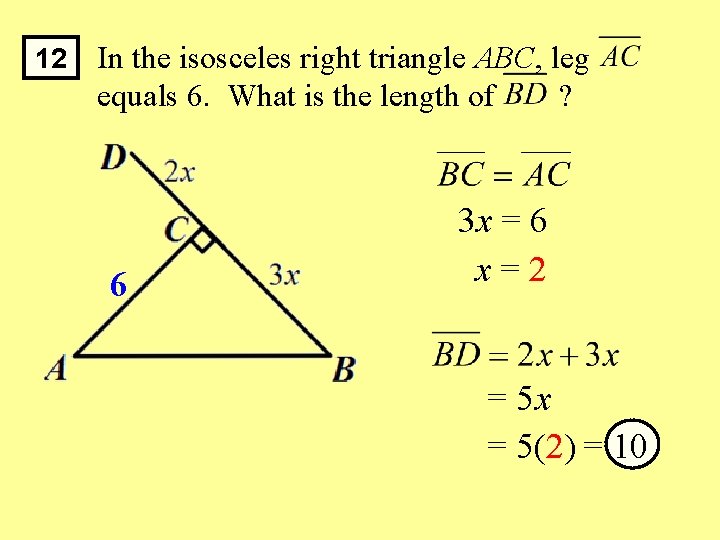
12 In the isosceles right triangle ABC, leg equals 6. What is the length of ? 6 3 x = 6 x=2 = 5 x = 5(2) = 10
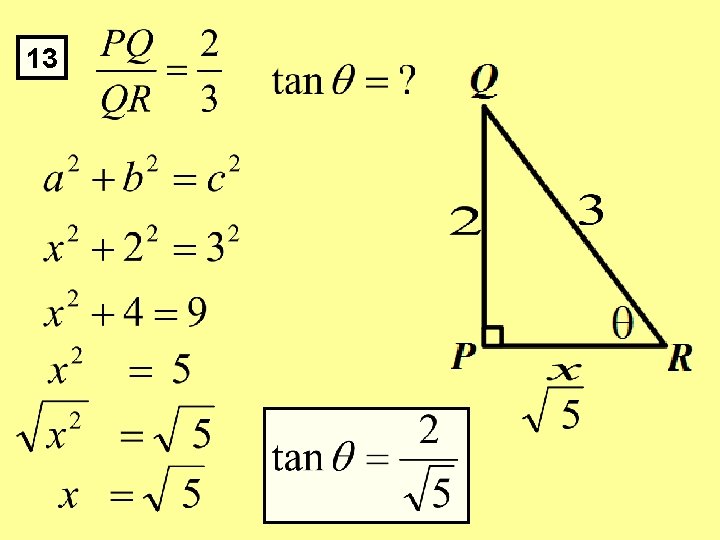
13

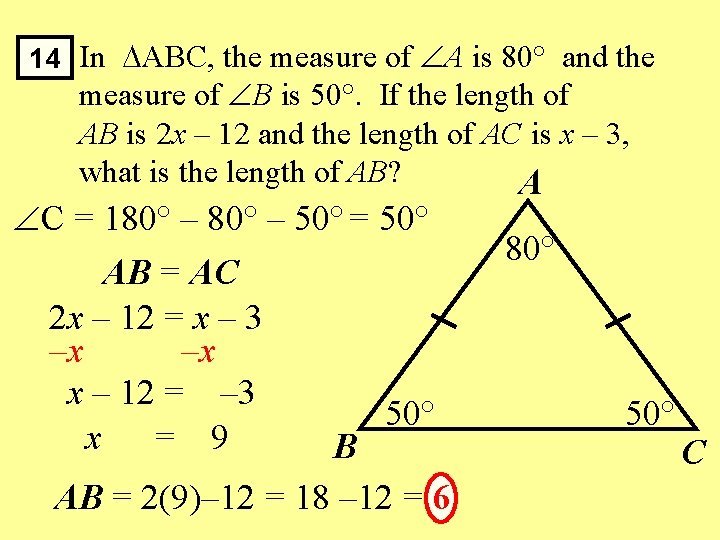
14 In ABC, the measure of A is 80° and the measure of B is 50°. If the length of AB is 2 x – 12 and the length of AC is x – 3, what is the length of AB? A C = 180° – 50° = 50° AB = AC 2 x – 12 = x – 3 –x –x x – 12 = – 3 50° x = 9 B AB = 2(9)– 12 = 18 – 12 = 6 80° 50° C

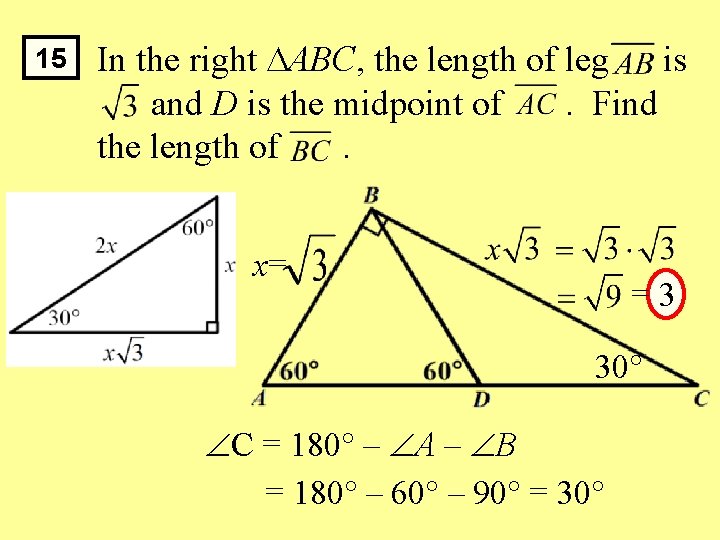
15 In the right ABC, the length of leg is and D is the midpoint of. Find the length of. x= =3 30° C = 180° – A – B = 180° – 60° – 90° = 30°

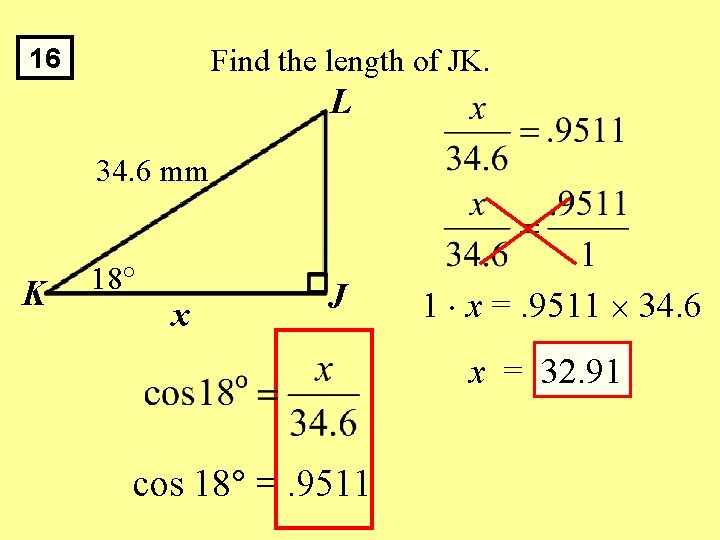
Find the length of JK. 16 L 34. 6 mm K 18 x J 1 x =. 9511 34. 6 x = 32. 91 cos 18 =. 9511

17 Two angles of a hexagon measure 140° each. The other four angles are equal in measure. What is the measure of each of the other four equal angles, in degrees? x x Step 1: Find the sum of interior angles in a hexagon. Number of sides = 6 140 x Number of sides – 2 =6– 2=4 Multiply 4 by 180 = 4(180 ) = 720

17 Two angles of a hexagon measure 140° each. The other four angles are equal in measure. What is the measure of each of the other four equal angles, in degrees? x 140 Step 1: Find the sum of interior angles in a hexagon. 720 Step 2: Set up equation by letting sum of angles equal 720. x + x + 140 = 720 4 x + 280 = 720 x x – 280 4 x = 440 Measure of each the four equal angles is 110 x = 110

18 A regular octagon is shown. What is the measure, in degrees, of X? Step 1: Find sum of the interior angles in the regular octagon. Number of sides = 8 X Number of sides – 2 = 8 – 2 = 6 Multiply 6 by 180 = 6(180 ) = 1080 Step 2: Find value of each interior angle, X. Divide sum by number of sides, 8. 1080 8 = 135

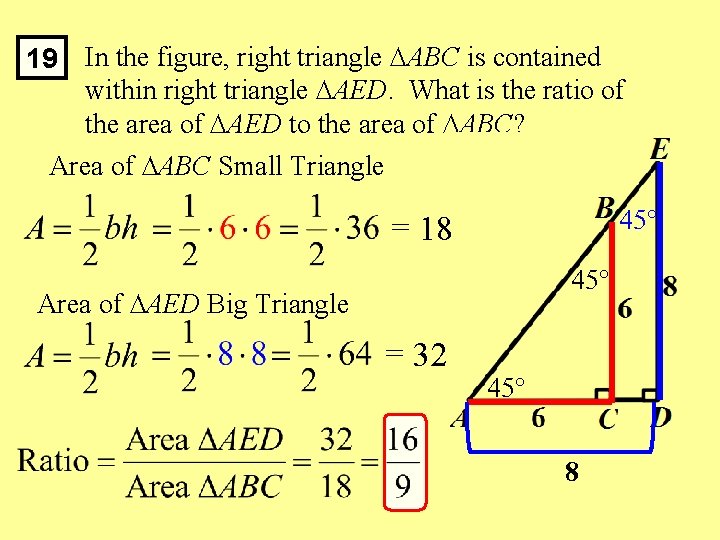
19 In the figure, right triangle ABC is contained within right triangle AED. What is the ratio of the area of AED to the area of ABC? ∆ABC is Isosceles 45 ∆AED Big Triangle 45 A = 45 D = 90 E = 45 ∆AED is Isosceles 45 8

19 In the figure, right triangle ABC is contained within right triangle AED. What is the ratio of the area of AED to the area of ABC? Area of ∆ABC Small Triangle 45 = 18 45 Area of ∆AED Big Triangle = 32 45 8

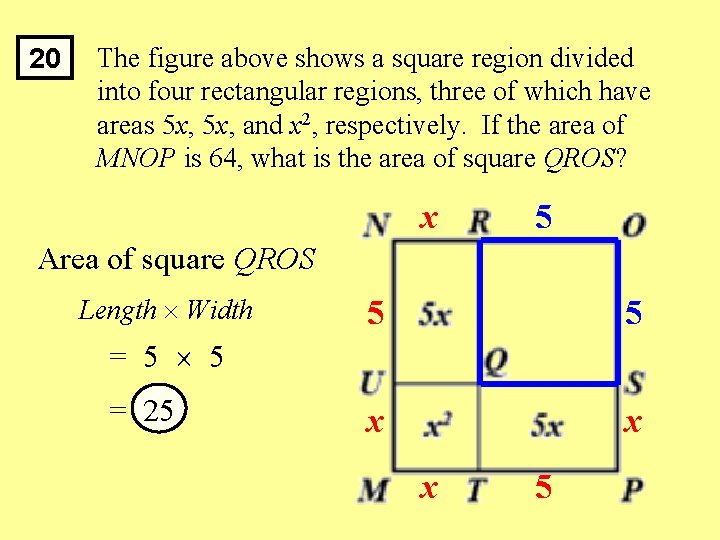
20 The figure above shows a square region divided into four rectangular regions, three of which have areas 5 x, and x 2, respectively. If the area of MNOP is 64, what is the area of square QROS? x 5 Area of square QROS Length Width 5 5 x x = 5 5 = 25 x 5

21 All the dimensions of a certain rectangular solid are integers greater than 1. If the volume is 126 cubic inches and the height is 6 inches, what is the perimeter of the base? V = Volume h 6 w Base l V = l w h 126 = l w 6 Perimeter of Base 2 l + 2 w = 2(7) + 2(3) = 14 + 6 21 = l w (Base) = 20 l = 3 or 7 w = 3 or 7

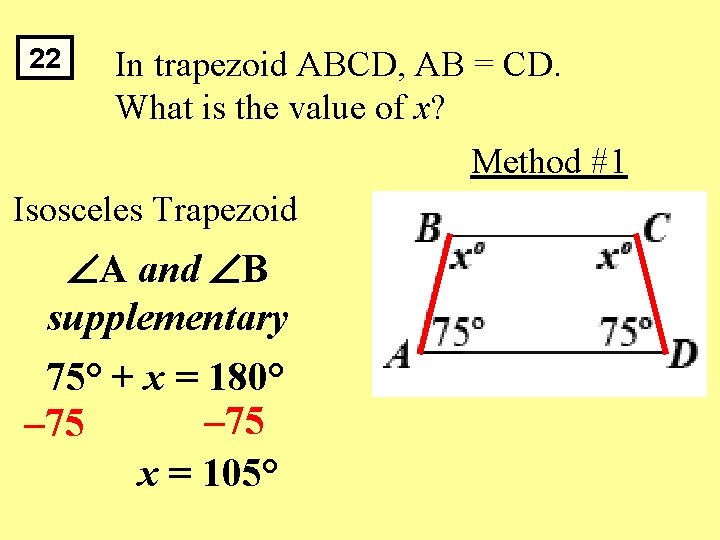
22 In trapezoid ABCD, AB = CD. What is the value of x? Method #1 Isosceles Trapezoid A and B supplementary 75° + x = 180° – 75 x = 105°

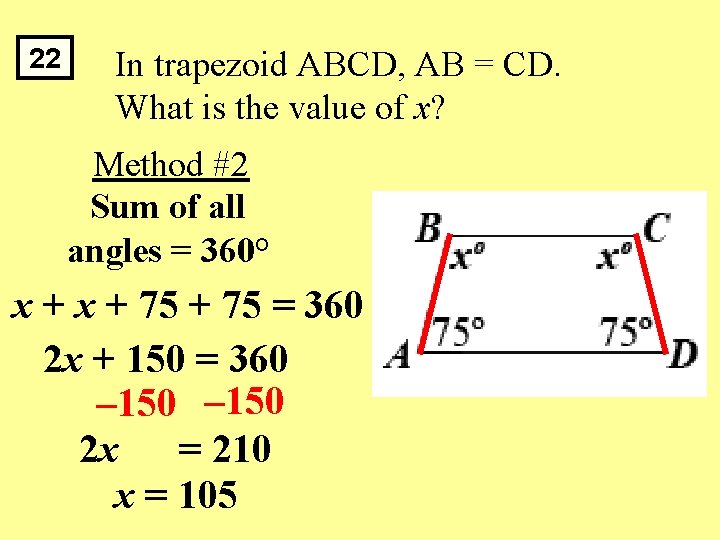
22 In trapezoid ABCD, AB = CD. What is the value of x? Method #2 Sum of all angles = 360° x + 75 = 360 2 x + 150 = 360 – 150 2 x = 210 x = 105

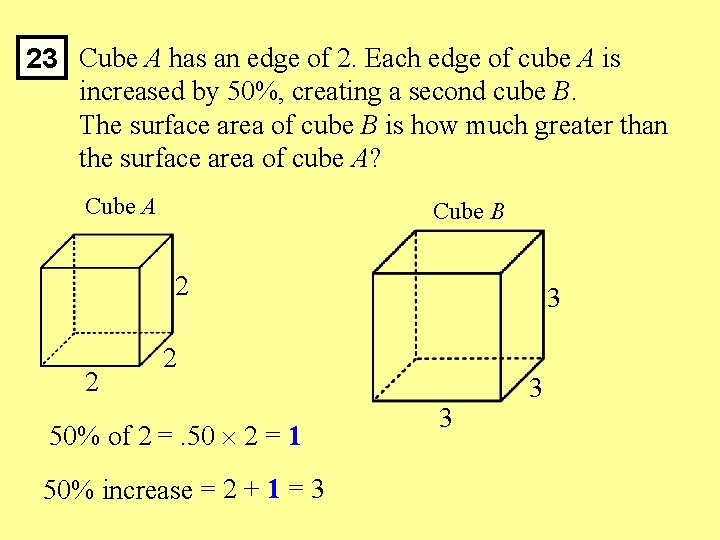
23 Cube A has an edge of 2. Each edge of cube A is increased by 50%, creating a second cube B. The surface area of cube B is how much greater than the surface area of cube A? Cube A Cube B 2 2 3 2 50% of 2 =. 50 2 = 1 50% increase = 2 + 1 = 3 3 3

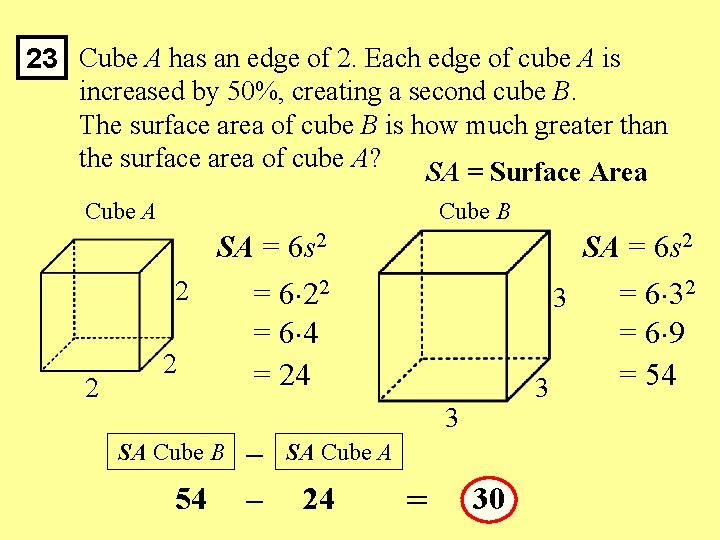
23 Cube A has an edge of 2. Each edge of cube A is increased by 50%, creating a second cube B. The surface area of cube B is how much greater than the surface area of cube A? SA = Surface Area Cube A Cube B SA = 6 s 2 2 SA = 6 s 2 = 6 22 = 6 4 = 24 3 3 3 SA Cube B 54 – – SA Cube A 24 = 30 = 6 32 = 6 9 = 54

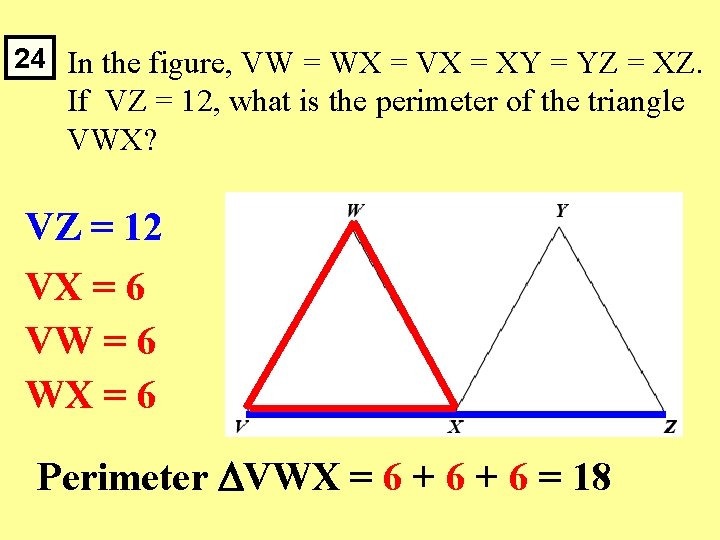
24 In the figure, VW = WX = VX = XY = YZ = XZ. If VZ = 12, what is the perimeter of the triangle VWX? VZ = 12 VX = 6 VW = 6 WX = 6 Perimeter VWX = 6 + 6 = 18

25 If the diameter of circle is 8, what is the ratio between the circle’s area and its circumference? d: diameter r: radius d = 2 r Step 1: Find the radius, given diameter is 8. d=8 r=4 Step 2 Find circumference of circle. C = 2πr = 2π 4 = 8π Step 3 Find area of circle. A = πr 2 = π 42 = π 16 = 16π

25 If the diameter of circle is 8, what is the ratio between the circle’s area and its circumference? Step 2 Find circumference of circle. C = 2πr = 2π 4 = 8π Step 3 Find area of circle. A = πr 2 = π 42 = π 16 = 16π Step 4: Find ratio. = 2: 1

26 Find the circumference of a circle with area π. C = 2πr C: Circumference A: Area Find the radius A = πr 2 C: Circumference A=π π = πr 2 C = 2πr C = 2π 1 1 = r 2 1 = r C = 2π

27 If a circle with an area of 4 is inscribed in a square , what is the perimeter of the square? 4 d=4 r=2 (Find radius) A: Area A = 4π A = πr 2 4π = πr 2 4 = r 2 2=r P: Perimeter P = 4 s P = 4(4) P = 16

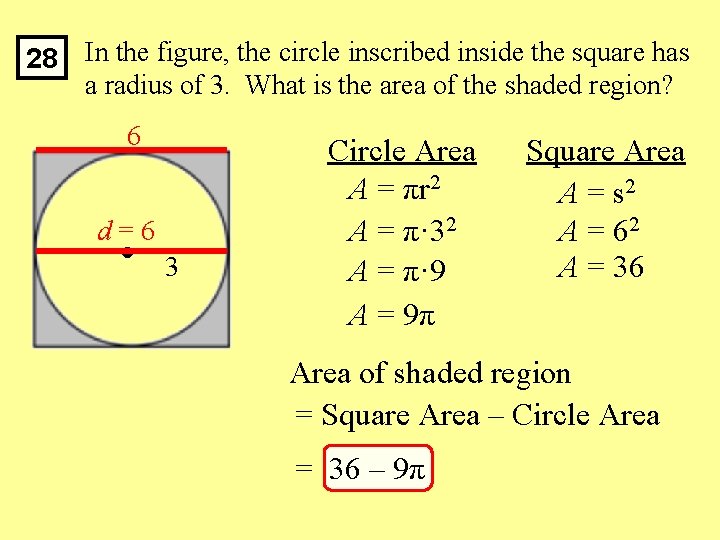
28 In the figure, the circle inscribed inside the square has a radius of 3. What is the area of the shaded region? 6 d=6 3 Circle Area A = πr 2 A = π· 32 A = π· 9 A = 9π Square Area A = s 2 A = 62 A = 36 Area of shaded region = Square Area – Circle Area = 36 – 9π

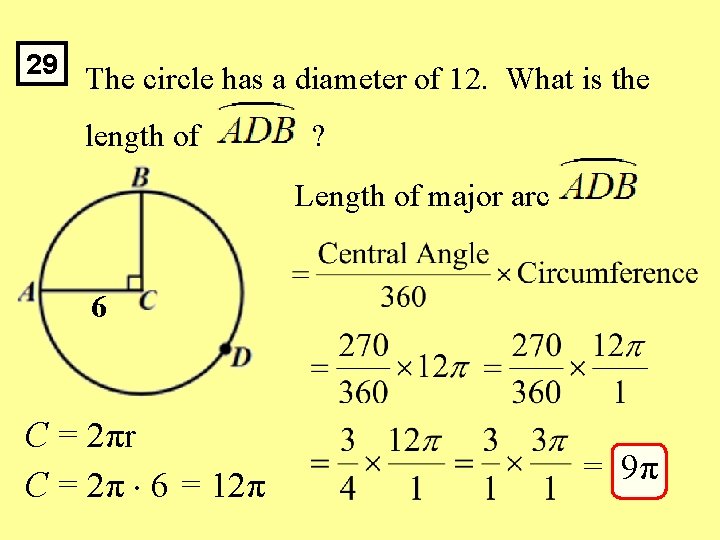
29 The circle has a diameter of 12. What is the length of ? Length of major arc 6 C = 2πr C = 2π 6 = 12π = 9π

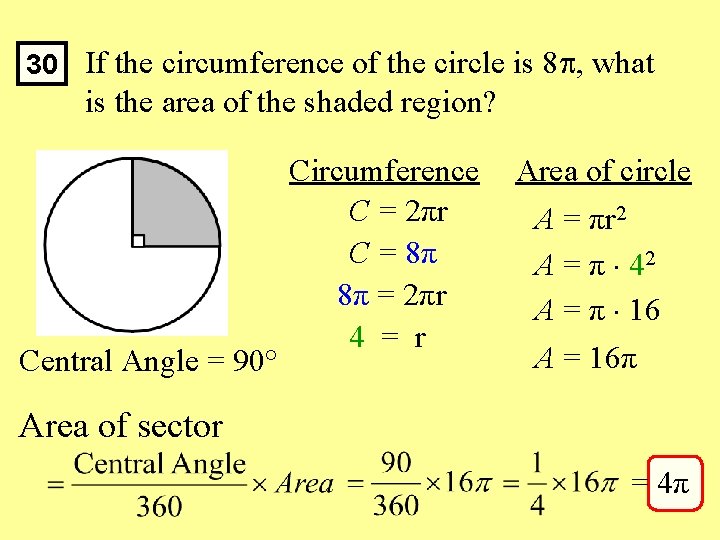
30 If the circumference of the circle is 8 , what is the area of the shaded region? Central Angle = 90° Circumference C = 2πr C = 8π 8π = 2πr 4 = r Area of circle A = πr 2 A = π 42 A = π 16 A = 16π Area of sector = 4π

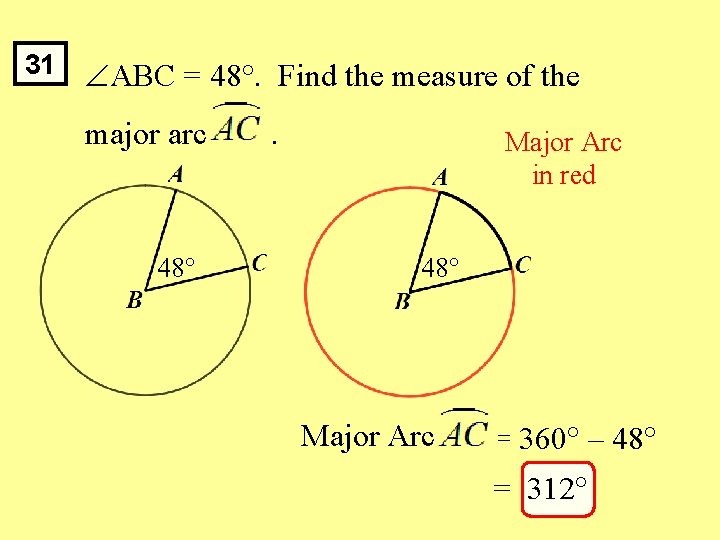
31 ABC = 48°. Find the measure of the major arc 48 . Major Arc in red 48 Major Arc = 360 – 48 = 312

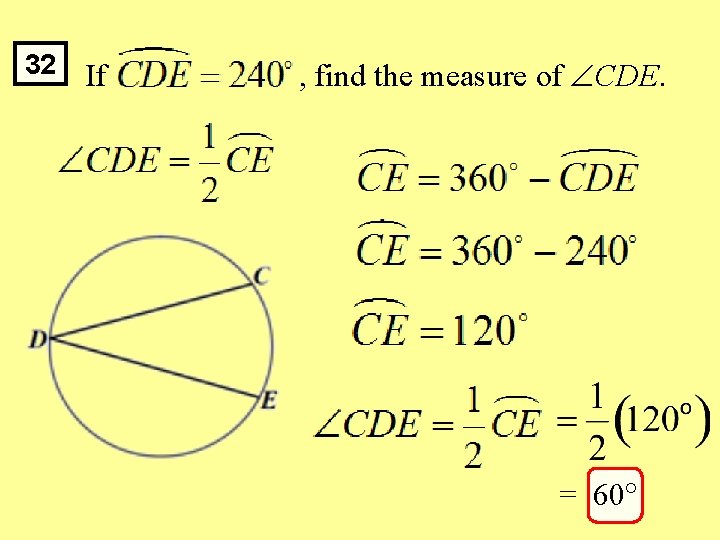
32 If , find the measure of CDE. = 60

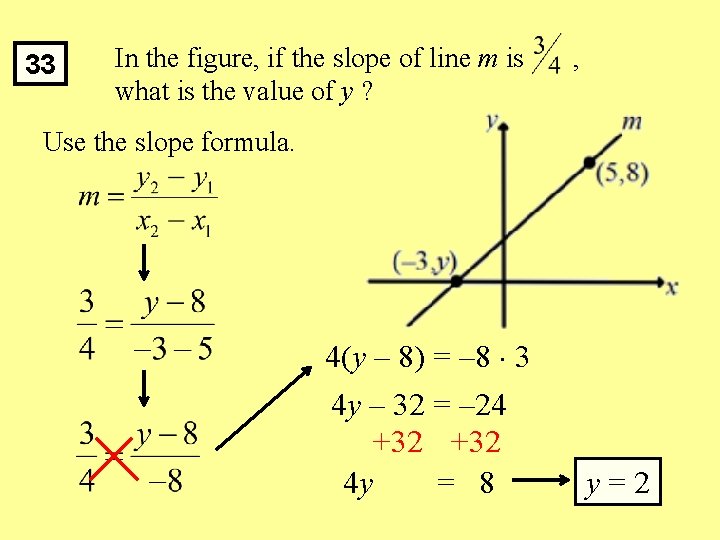
33 In the figure, if the slope of line m is what is the value of y ? , Use the slope formula. 4(y – 8) = – 8 3 4 y – 32 = – 24 +32 4 y = 8 y=2

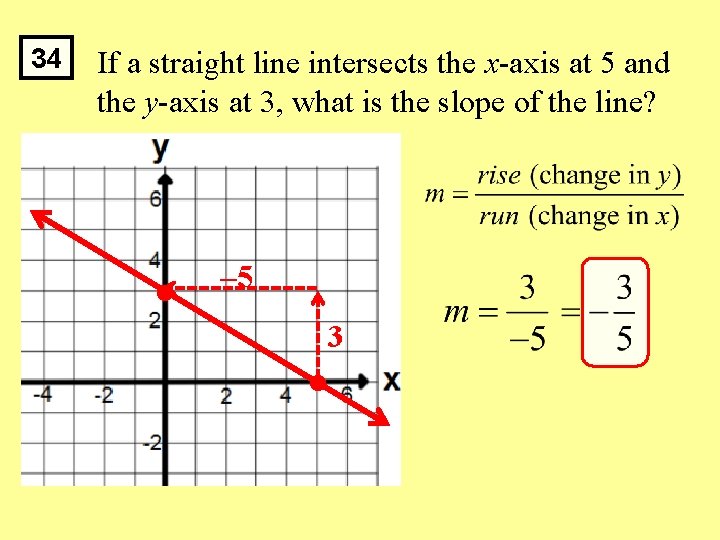
34 If a straight line intersects the x-axis at 5 and the y-axis at 3, what is the slope of the line? – 5 3

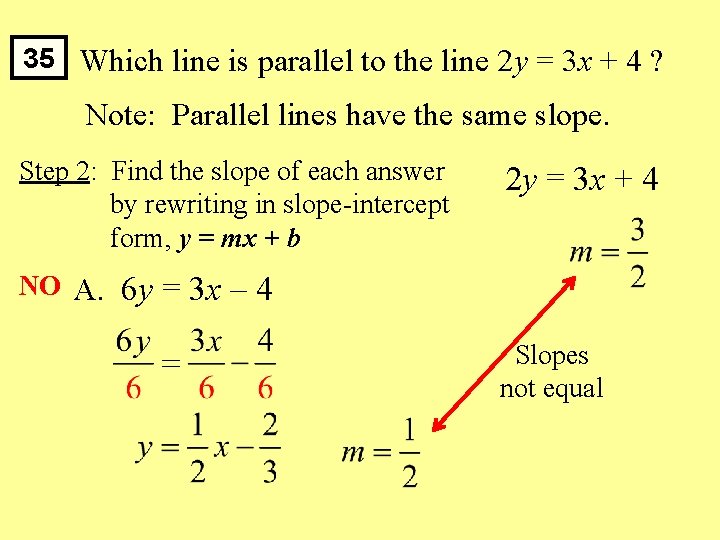
35 Which line is parallel to the line 2 y = 3 x + 4 ? Note: Parallel lines have the same slope. A. 6 y = 3 x – 4 B. 2 y = x + 2 C. 4 y = 6 x – 1 D. y = 3 x + 4 E. 2 y = – 2 x – 1 Step 1: Find the slope of 2 y = 3 x + 4 by rewriting in slope-intercept form, y = mx + b 2 y = 3 x + 4

35 Which line is parallel to the line 2 y = 3 x + 4 ? Note: Parallel lines have the same slope. Step 2: Find the slope of each answer by rewriting in slope-intercept form, y = mx + b NO A. 2 y = 3 x + 4 6 y = 3 x – 4 Slopes not equal

35 Which line is parallel to the line 2 y = 3 x + 4 ? Note: Parallel lines have the same slope. Step 2: Find the slope of each answer by rewriting in slope-intercept form, y = mx + b NO B. 2 y = 3 x + 4 2 y = x + 2 Slopes not equal

35 Which line is parallel to the line 2 y = 3 x + 4 ? Note: Parallel lines have the same slope. Step 2: Find the slope of each answer by rewriting in slope-intercept form, y = mx + b 2 y = 3 x + 4 C. 4 y = 6 x – 1 Slopes are equal

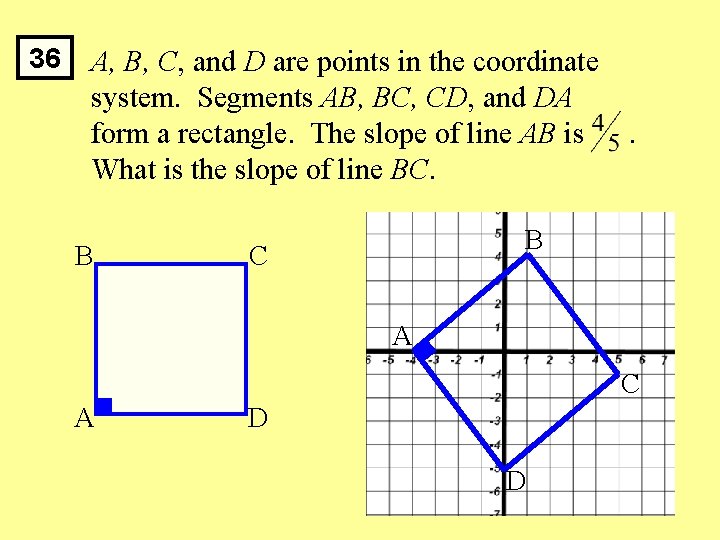
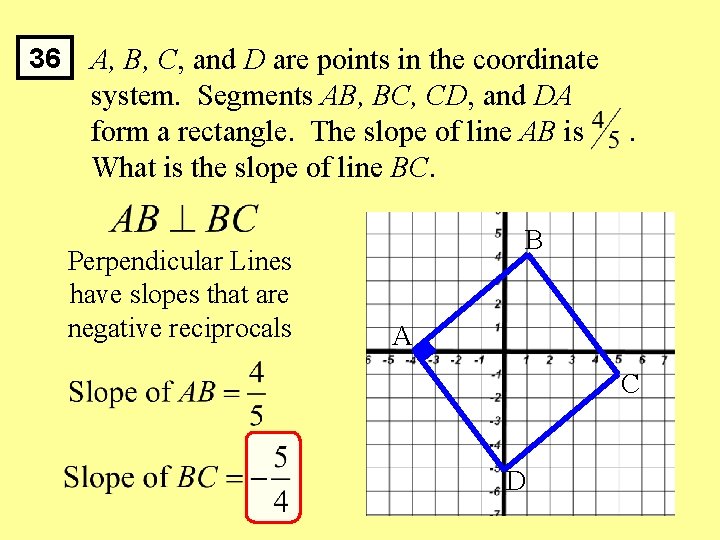
36 A, B, C, and D are points in the coordinate system. Segments AB, BC, CD, and DA form a rectangle. The slope of line AB is What is the slope of line BC. B . B C A D D

36 A, B, C, and D are points in the coordinate system. Segments AB, BC, CD, and DA form a rectangle. The slope of line AB is What is the slope of line BC. Perpendicular Lines have slopes that are negative reciprocals . B A C D

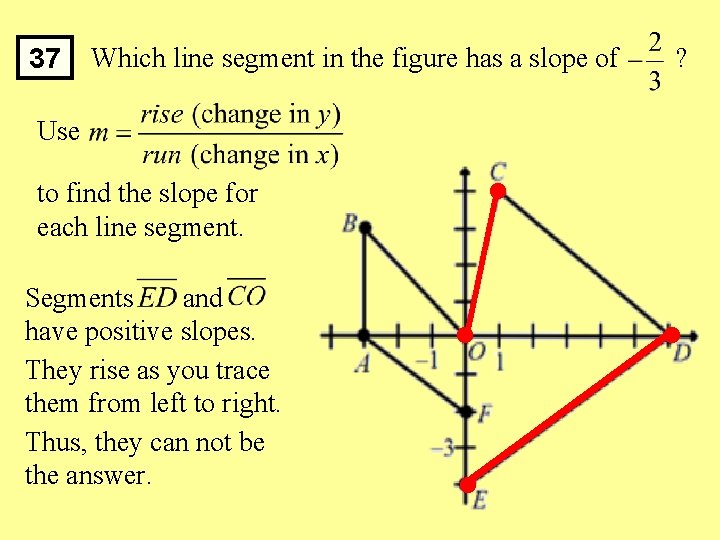
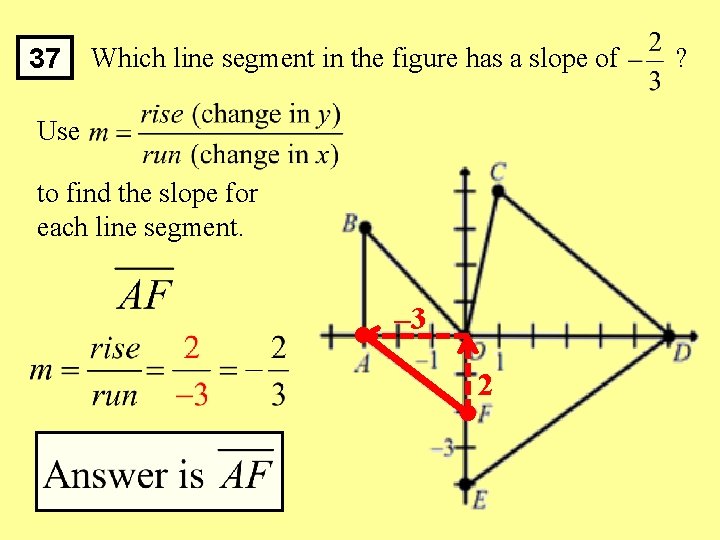
37 Which line segment in the figure has a slope of ? Use to find the slope for each line segment. Segments and have positive slopes. They rise as you trace them from left to right. Thus, they can not be the answer.

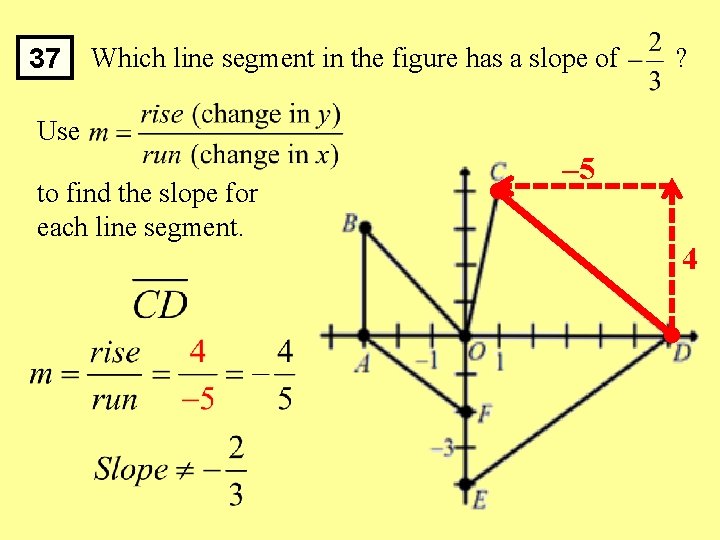
37 Which line segment in the figure has a slope of ? Use to find the slope for each line segment. – 5 4

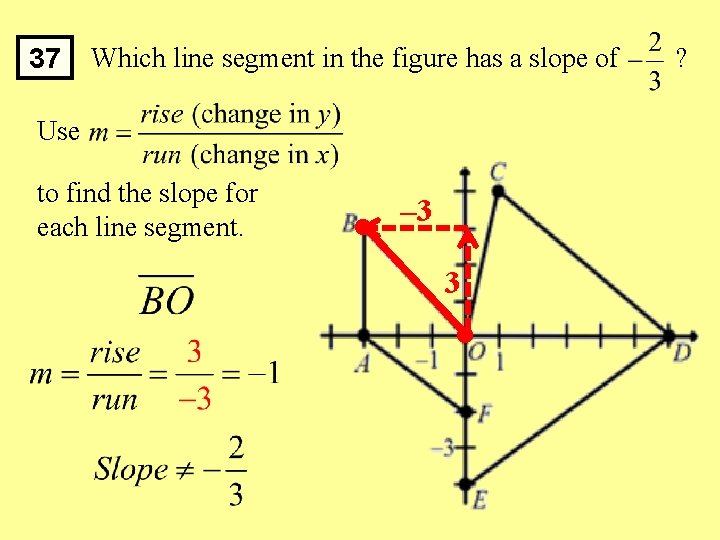
37 Which line segment in the figure has a slope of Use to find the slope for each line segment. – 3 3 ?

37 Which line segment in the figure has a slope of Use to find the slope for each line segment. – 3 2 ?

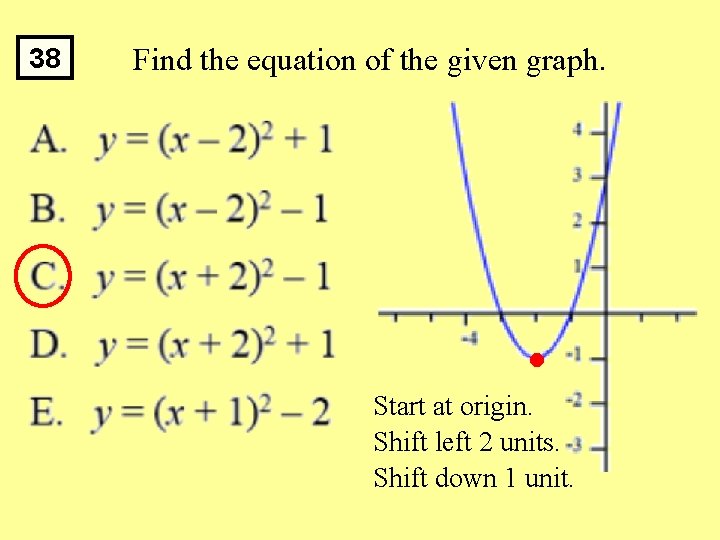
38 Find the equation of the given graph. Start at origin. Shift left 2 units. Shift down 1 unit.

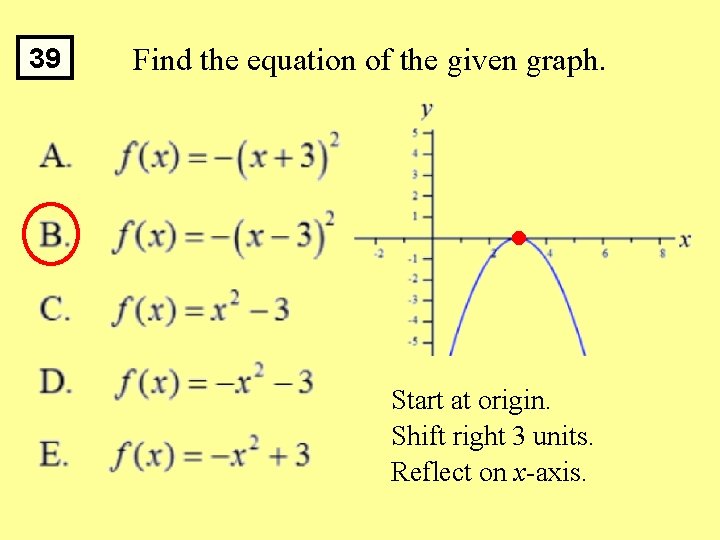
39 Find the equation of the given graph. Start at origin. Shift right 3 units. Reflect on x-axis.

40 A parabola with in equation of the form y = ax 2 + bx + c has the point (3, 1) as its vertex. If (1, 3) also lies on the parabola, which of the following is another point on this parabola? Mirror Image Points x=1 (1, 3) x=3 x=5 (? , 3) (5, 3) x-coordinates are same distance from axis of symmetry (3, 1)

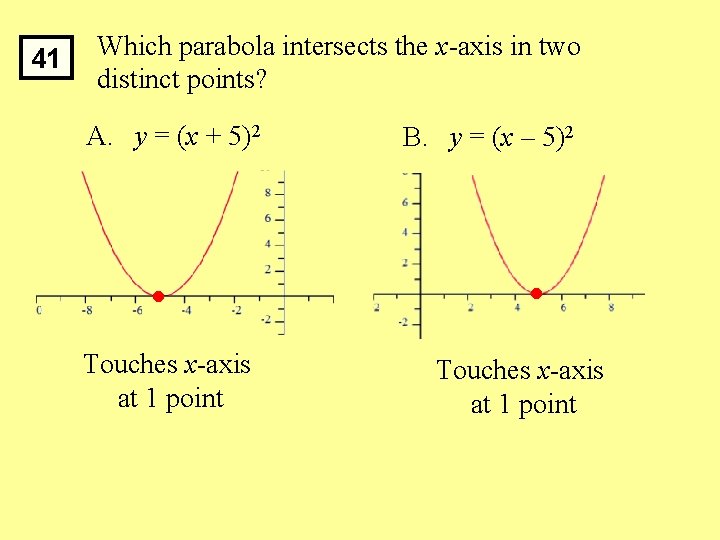
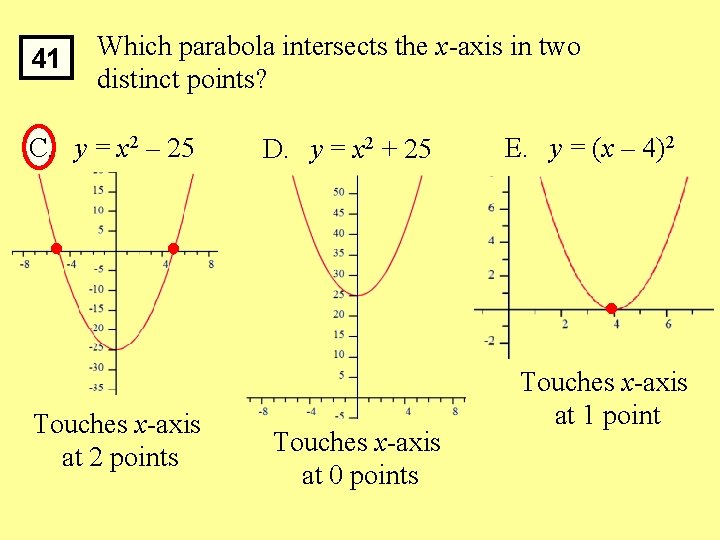
41 Which parabola intersects the x-axis in two distinct points? A. y = (x + 5)2 Touches x-axis at 1 point B. y = (x – 5)2 Touches x-axis at 1 point

41 Which parabola intersects the x-axis in two distinct points? C. y = x 2 – 25 D. y = x 2 + 25 E. y = (x – 4)2 Touches x-axis at 2 points Touches x-axis at 0 points Touches x-axis at 1 point

42 Which of the following are solutions to the equation x 2 + 2 x = 8 ? Substitute each answer for x into equation x 2 + 2 x = 8. Then, determine if both sides are equal. A. – 8 and 1 NO B. – 1 and 8 C. – 4 and – 2 D. 4 and – 2 E. – 4 and 2 Test x = 1 x 2 + 2 x = 8 (1)2 + 2(1) = 8 1+2=8 3 8 Test x = – 8 x 2 + 2 x = 8 (– 8)2 + 2(– 8) = 8 64 + (– 16) = 8 48 8

42 Which of the following are solutions to the equation x 2 + 2 x = 8 ? Substitute each answer for x into equation x 2 + 2 x = 8. Then, determine if both sides are equal. A. – 8 and 1 NO Test x = 8 2 + 2 x = 8 x NO B. – 1 and 8 (8)2 + 2(8) = 8 C. – 4 and – 2 64 + 16 = 8 D. 4 and – 2 80 8 E. – 4 and 2 If one answer does not work, then the whole answer is wrong.

42 Which of the following are solutions to the equation x 2 + 2 x = 8 ? Substitute each answer for x into equation x 2 + 2 x = 8. Then, determine if both sides are equal. A. – 8 and 1 NO B. – 1 and 8 NO C. – 4 and – 2 NO D. 4 and – 2 NO E. – 4 and 2 Test x = – 2 If one answer x 2 + 2 x = 8 does not work, 2 (– 2) + 2(– 2) = 8 then the whole 4 + (– 4) = 8 answer is wrong. 0 8

42 Which of the following are solutions to the equation x 2 + 2 x = 8 ? Substitute each answer for x into equation x 2 + 2 x = 8. Then, determine if both sides are equal. A. – 8 and 1 NO Test x = 2 2 + 2 x = 8 x NO B. – 1 and 8 (2)2 + 2(2) = 8 C. – 4 and – 2 NO 4+4=8 D. 4 and – 2 NO 8=8 E. – 4 and 2 Test x = – 4 x 2 + 2 x = 8 (– 4)2 + 2(– 4) = 8 16 + (– 8) = 8 8=8