Practice session 6 The environment model Environment Model

  • Slides: 17
Download presentation
Practice session #6: The environment model

Practice session #6: The environment model

Environment Model: Introduction Environments: • Frame: GE Maps variables to values (i. e. ,

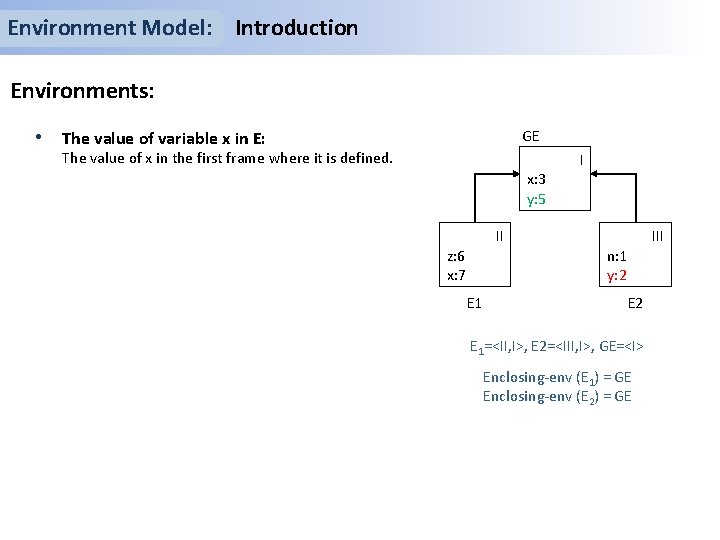
Environment Model: Introduction Environments: • Frame: GE Maps variables to values (i. e. , every variable in a frame has a single value). x: 3 y: 5 • Environment: A finite linked list of frames, where the last frame is the global environment. • The global environment: A single-frame environment, the only environment that statically exists. • Enclosing environment of E: E, excluding its first frame. II z: 6 x: 7 E 1 I n: 1 y: 2 E 1=<II, I>, E 2=<III, I>, GE=<I> Enclosing-env (E 1) = GE Enclosing-env (E 2) = GE III

Environment Model: Introduction Environments: • The value of variable x in E: GE The

Environment Model: Introduction Environments: • The value of variable x in E: GE The value of x in the first frame where it is defined. x: 3 y: 5 II z: 6 x: 7 E 1 I n: 1 y: 2 E 1=<II, I>, E 2=<III, I>, GE=<I> Enclosing-env (E 1) = GE Enclosing-env (E 2) = GE III

Environment Model: Introduction Closure: A complex data structure with: (1) Procedure parameters. (2) Procedure

Environment Model: Introduction Closure: A complex data structure with: (1) Procedure parameters. (2) Procedure body. (3) The environment at the time it was created. b 1 > (define square (lambda (x) (* x x))) > (lambda (y) y) b 2 GE square: p: (x) b 1: (* x x) p: (y) b 2: y

Environment Model: Introduction Procedure application: (1) Create new frame, mapping the procedure params to

Environment Model: Introduction Procedure application: (1) Create new frame, mapping the procedure params to application values. (2) The new frame extends the environment associated with the procedure. (3) Evaluate the body of the procedure in the new environment. b 1 > (define square (lambda (x) (* x x))) > (square 5) GE square: p: (x) b 1: (* x x) E 1 b 1 x: 5 GE

Environment Model: Recursion GE fact: p: (n) b: (if…) E 1 b n: 3

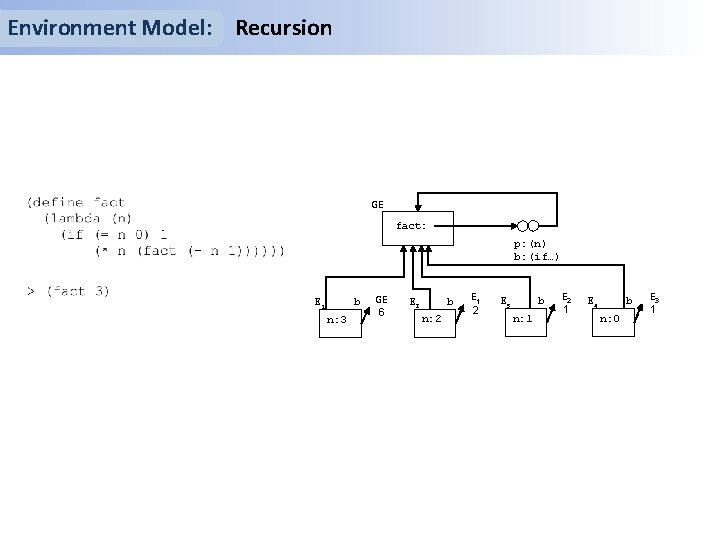
Environment Model: Recursion GE fact: p: (n) b: (if…) E 1 b n: 3 GE 6 E 2 b n: 2 E 1 2 E 3 b n: 1 E 2 1 E 4 b n: 0 E 3 1

Environment Model: Definition and Application GE sq: p: (x) b 1: (* x x)

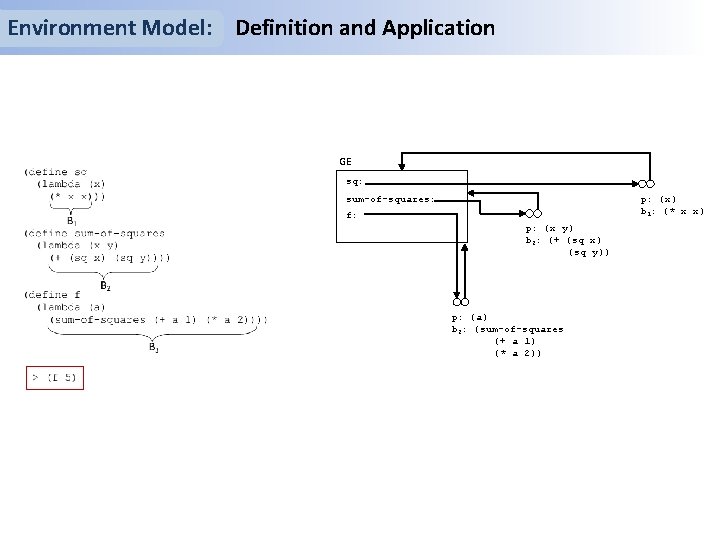
Environment Model: Definition and Application GE sq: p: (x) b 1: (* x x) sum-of-squares: f: p: (x y) b 2: (+ (sq x) (sq y)) p: (a) b 3: (sum-of-squares (+ a 1) (* a 2))

Environment Model: Definition and Application GE sq: p: (x) b 1: (* x x)

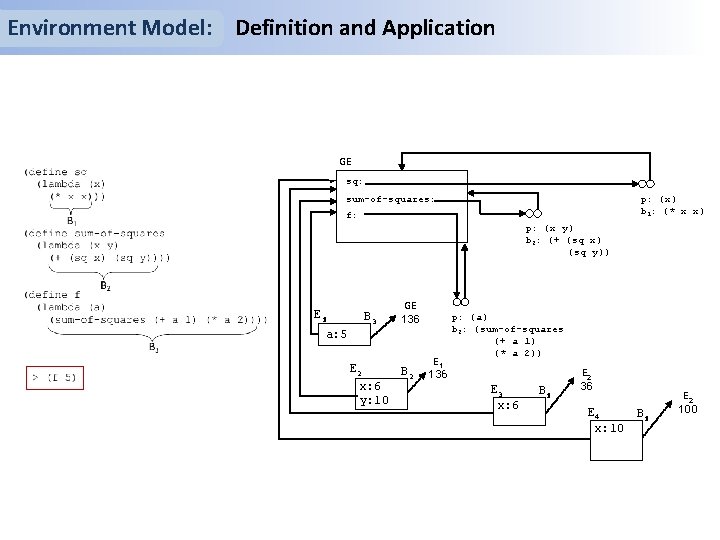
Environment Model: Definition and Application GE sq: p: (x) b 1: (* x x) sum-of-squares: f: p: (x y) b 2: (+ (sq x) (sq y)) E 1 B 3 GE 136 a: 5 E 2 x: 6 y: 10 B 2 E 1 136 p: (a) b 3: (sum-of-squares (+ a 1) (* a 2)) E 3 x: 6 B 1 E 2 36 E 4 x: 10 B 1 E 2 100

Environment Model: Definition and Let GE a: 8 b: 5 c: 8 f: p:

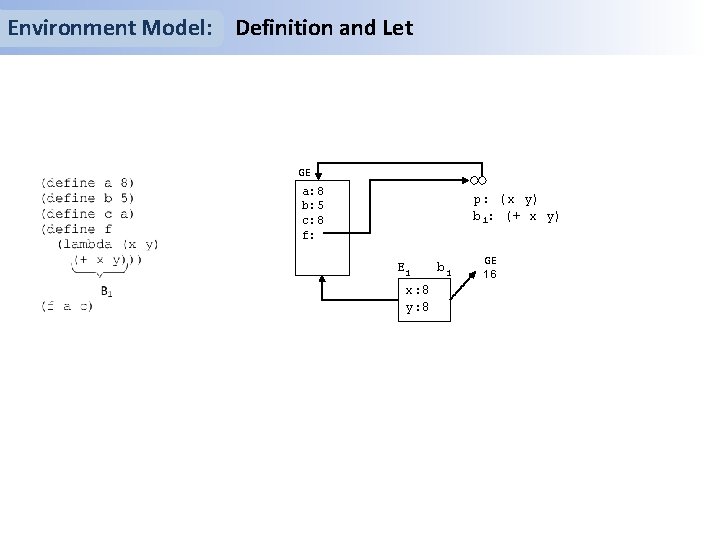
Environment Model: Definition and Let GE a: 8 b: 5 c: 8 f: p: (x y) b 1: (+ x y) E 1 x: 8 y: 8 b 1 GE 16

Environment Model: Definition and Let GE a: 8 b: 5 c: 8 f: p:

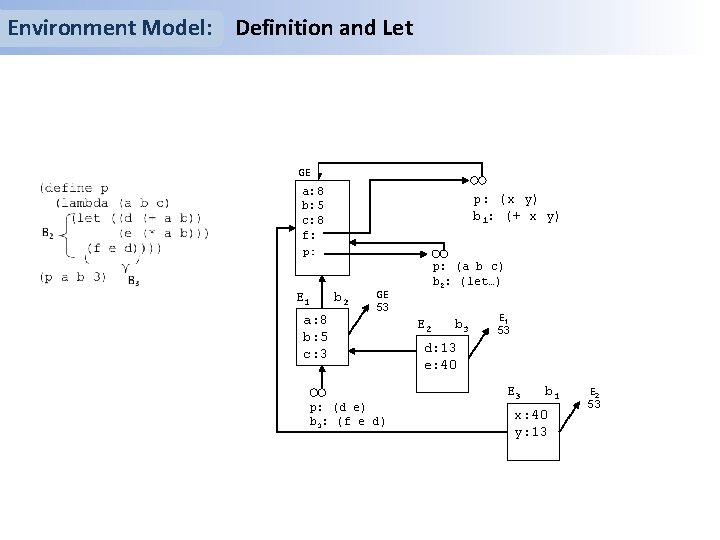
Environment Model: Definition and Let GE a: 8 b: 5 c: 8 f: p: (x y) b 1: (+ x y) p: E 1 b 2 a: 8 b: 5 c: 3 p: (a b c) b 2: (let…) GE 53 p: (d e) b 3: (f e d) E 2 b 3 E 1 53 d: 13 e: 40 E 3 b 1 x: 40 y: 13 E 2 53

Environment Model: Pair ADT, Lazy implementation GE make-pair: P 1: E 1 b 1

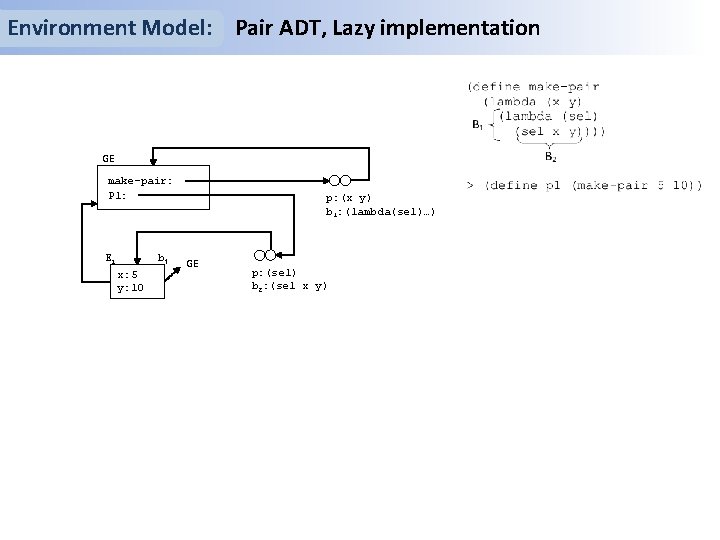
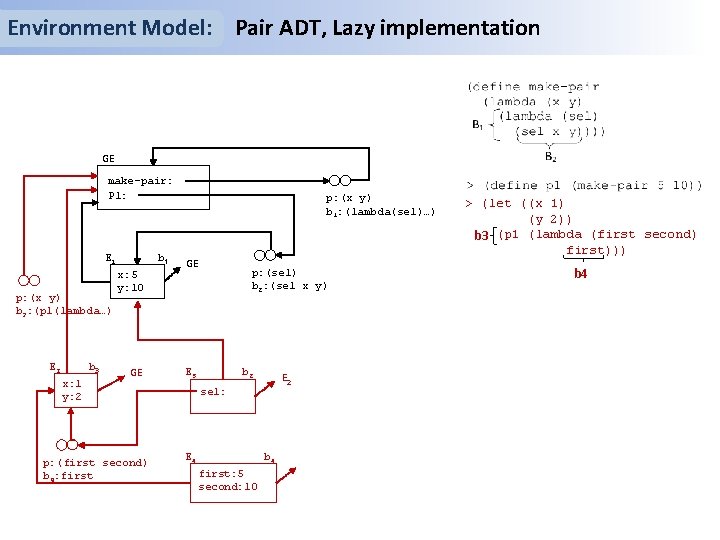
Environment Model: Pair ADT, Lazy implementation GE make-pair: P 1: E 1 b 1 x: 5 y: 10 p: (x y) b 1: (lambda(sel)…) GE p: (sel) b 2: (sel x y)

Environment Model: Pair ADT, Lazy implementation GE make-pair: P 1: E 1 x: 5

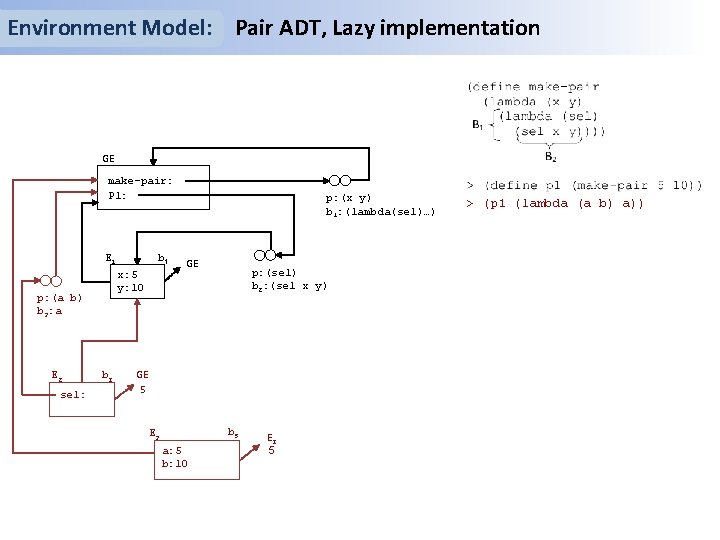
Environment Model: Pair ADT, Lazy implementation GE make-pair: P 1: E 1 x: 5 y: 10 p: (a b) b 3: a E 2 sel: b 1 b 2 p: (x y) b 1: (lambda(sel)…) GE p: (sel) b 2: (sel x y) GE 5 b 3 E 3 a: 5 b: 10 E 2 5 > (p 1 (lambda (a b) a))

Environment Model: Pair ADT, Lazy implementation GE make-pair: P 1: E 1 p: (x

Environment Model: Pair ADT, Lazy implementation GE make-pair: P 1: E 1 p: (x y) b 3: (p 1(lambda…) E 2 b 3 x: 1 y: 2 b 1 x: 5 y: 10 GE p: (first second) b 4: first p: (x y) b 1: (lambda(sel)…) GE p: (sel) b 2: (sel x y) E 3 b 2 E 2 sel: E 4 b 4 first: 5 second: 10 > (let ((x 1) (y 2)) b 3 (p 1 (lambda (first second) first))) b 4

Environment Model: box, set-box!, set! Box: • Required to wrap a variable so it

Environment Model: box, set-box!, set! Box: • Required to wrap a variable so it can be accessed and changed, much like pointers. • In the box environment model, it is used to enable mutation (seen in class) • Box is defined by the interface: (box v) - value constructor (box? x) - type predicate (unbox b) - accessor (set-box!) - mutator set! • A way to change the value of an existing variable. For example: > (define x 5) > x 5 > (set! x 80) > x 80 > (set! y 5) Error: cannot set variable before its definition

Environment Model: set! vs set-box! Example 1: counter (set! vs set-box!) (define counter (let

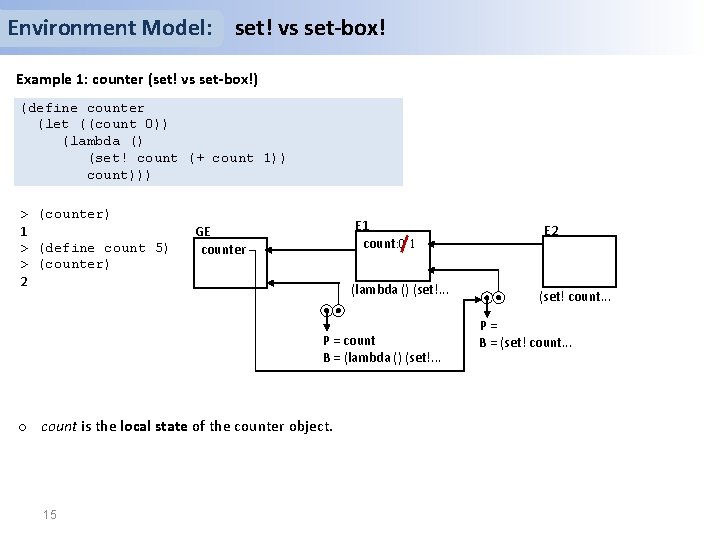
Environment Model: set! vs set-box! Example 1: counter (set! vs set-box!) (define counter (let ((count 0)) (lambda () (set! count (+ count 1)) count))) > (counter) 1 > (define count 5) > (counter) 2 E 1 count: 0 1 GE counter (lambda () (set!. . . P = count B = (lambda () (set!. . . o count is the local state of the counter object. 15 E 2 (set! count. . . P= B = (set! count. . .

Environment Model: set! vs set-box! Example 1: counter (set! vs set-box!) > (counter (lambda(x)

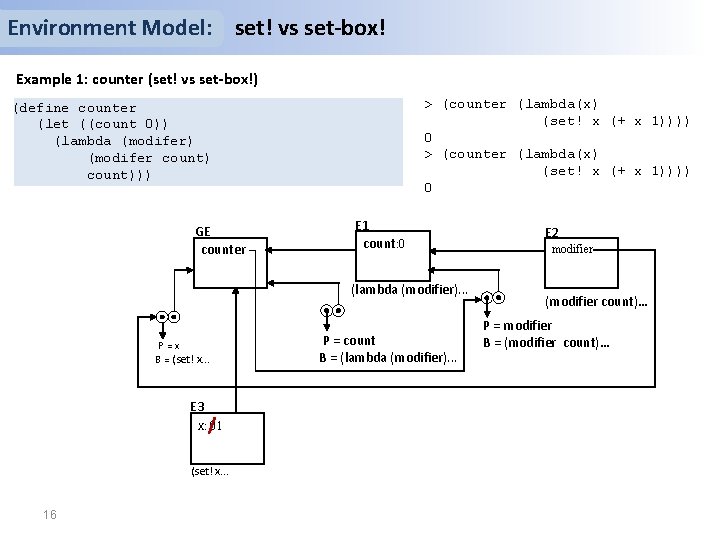
Environment Model: set! vs set-box! Example 1: counter (set! vs set-box!) > (counter (lambda(x) (set! x (+ x 1)))) 0 (define counter (let ((count 0)) (lambda (modifer) (modifer count))) GE counter E 1 count: 0 (lambda (modifier). . . P=x B = (set! x. . . E 3 x: 0 1 (set! x. . . 16 P = count B = (lambda (modifier). . . E 2 modifier (modifier count)… P = modifier B = (modifier count)…

Environment Model: set! vs set-box! Example 1: counter (set! vs set-box!) > (counter (lambda(x)

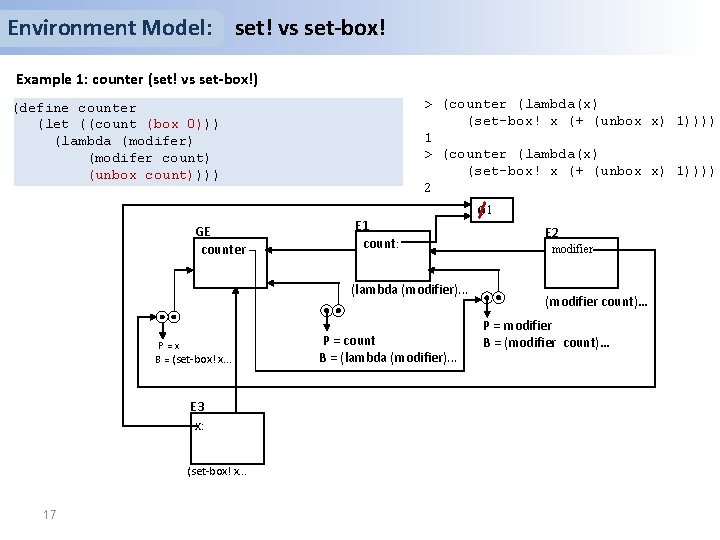
Environment Model: set! vs set-box! Example 1: counter (set! vs set-box!) > (counter (lambda(x) (set-box! x (+ (unbox x) 1)))) 1 > (counter (lambda(x) (set-box! x (+ (unbox x) 1)))) 2 (define counter (let ((count (box 0))) (lambda (modifer) (modifer count) (unbox count)))) GE counter E 1 count: (lambda (modifier). . . P=x B = (set-box! x. . . E 3 x: (set-box! x. . . 17 P = count B = (lambda (modifier). . . 01 E 2 modifier (modifier count)… P = modifier B = (modifier count)…

Practice Practice Practice Practice Practice Describe how thePractice Practice Practice Practice Practice Describe how the
ENVIRONMENT ENVIRONMENT Define environment ENVIRONMENT Environment the socialENVIRONMENT ENVIRONMENT Define environment ENVIRONMENT Environment the social
BUSINESS ENVIRONMENT BUSINESS ENVIRONMENT What is Environment EnvironmentBUSINESS ENVIRONMENT BUSINESS ENVIRONMENT What is Environment Environment
Analyzing Marketing Environment ENVIRONMENT Macro Environment Micro EnvironmentAnalyzing Marketing Environment ENVIRONMENT Macro Environment Micro Environment
Cookie Session Cookie Cookie Cookie Session Session sessionCookie Session Cookie Cookie Cookie Session Session session
Cookie Session Cookie Cookie Cookie Session Session sessionCookie Session Cookie Cookie Cookie Session Session session
Cookie Session Cookie Cookie Session Session session IECookie Session Cookie Cookie Session Session session IE
PRACTICE PRACTICE AND MORE PRACTICE WRITE IT DOWNPRACTICE PRACTICE AND MORE PRACTICE WRITE IT DOWN
PRACTICE SUPERVISOR PRACTICE ASSESSOR TRANSITION FOR PRACTICE TEACHERSPRACTICE SUPERVISOR PRACTICE ASSESSOR TRANSITION FOR PRACTICE TEACHERS
Practice Question Practice Question 12 34 Practice QuestionPractice Question Practice Question 12 34 Practice Question
Practice Management Practice Management Practice Structure There arePractice Management Practice Management Practice Structure There are
Practice Question Practice Question 12 34 Practice QuestionPractice Question Practice Question 12 34 Practice Question
th 6 Grade Round 1 Practice Practice Practiceth 6 Grade Round 1 Practice Practice Practice
Massage Practice Settings Practice Settings Private Practice homeMassage Practice Settings Practice Settings Private Practice home
Practice First When you complete a practice sessionPractice First When you complete a practice session
Session 11 Testing Subjects Practice First Session 2Session 11 Testing Subjects Practice First Session 2