Practice session 5 Compund Data ADT 1 Compound

Practice session #5: Compund Data, ADT: 1. Compound types: Pair, List 2. Data abstraction: • The ADT concept • separating usage from implementation 3. Procedural implementation of ADTs 4. Type inference system: Implementation with ADTs hierarchy

1. Compound data types The Pair type: Represents an ordered pair of values (of any type). Value constructor: cons, type: [T 1 * T 2 -> Pair(T 1, T 2)] Selectors: car, type: [Pair(T 1, T 2) -> T 1] cdr, type: [Pair(T 1, T 2) -> T 2] Examples: > (cons 1 2) ‘(1. 2) > (cons 1 (cons 2 (lambda () (+ 1 2)))) > ‘(1 2. #<procedure>) Q: Why not ‘(1. 2. #<procedure>) ? 2 Box-representation:

1. Compound data types The Pair type: Represents an ordered pair of values (of any type). More examples: > (cons (car (cons 1 2)) (cdr (cons 3 4))) '(1. 4) > (define c (cons 1 (cons 'cat (cons 3 (cons 4 5))))) > c '(1 cat 3 4. 5) > (cdr c))) '(4. 5) > (cdddr c) '(4. 5) > (car (cdr c)) 'cat > (cadr c) 'cat > (cons 1 2) (cons 1 3)) '((1. 2) 1. 3) 3

1. Compound data types The List type: The List type is define recursively: 1. A Pair, (cons head tail), where head is any element, and tail is a List. 2. The last element in a list is the empty list. Homogeneous list: • A list of which all elements are of the same type, T. • The type for such a list is denoted List(T). Heterogeneous list: • A list that consists of elements of different types. • The type of an homogeneous list is LIST. 4

1. Compound data types The List type: Value constructors: Examples: cons, type: [T *List(T) -> List( T)] > ( define a (cons 3 (cons 4 (cons 5 ‘()))) ) > a ‘(3 4 5) list, type: [T*T*…*T -> List(T)] > (cons 1 a) ‘(1 3 4 5) type: [T *List -> List] type: [T 1 *List(T 2) -> List], T 1≠T 2 type: [T 1*T 2*…*Tn -> List] type: [Empty -> List(T)] type: [Empty -> List] > (list 1 2 4) ‘(1 2 4) > (list) ‘() Q: What is the difference between ‘() and (list)? 5

1. Compound data types The List type: Selectors: Examples: car, type: [List(T) -> T] type: [List -> T] > (define L 1 (list)) > (null? L 1) #t > (length L 1) 0 > (define L 2 (list 1 (list 2 3) 6)) > L 2 '(1 (2 3) 6) > (car L 2) 1 > (caadr L 2) 2 > (cadadr L 2) 3 > (cdddr L 2) '() cdr, type: [List(T) -> List(T)] type: [List -> List] Predicates: list? , type: [T -> Boolean] null? , type: [List(T) -> Boolean] type: [List -> Boolean] equal? , type: [List(T) * List(T) -> Boolean] type: [List * List -> Boolean] 6

1. Compound data types The List type: Selectors: Examples: car, type: [List(T) -> T] type: [List -> T] > (list? (cons 2 (cons (list 2 3) 4))) #f cdr, type: [List(T) -> List(T)] type: [List -> List] > (list 1 2) '((1 2) Predicates: list? , type: [T -> Boolean] null? , type: [List(T) -> Boolean] type: [List -> Boolean] equal? , type: [List(T) * List(T) -> Boolean] type: [List * List -> Boolean] 7 Additional operations: - append - length - list-ref - …

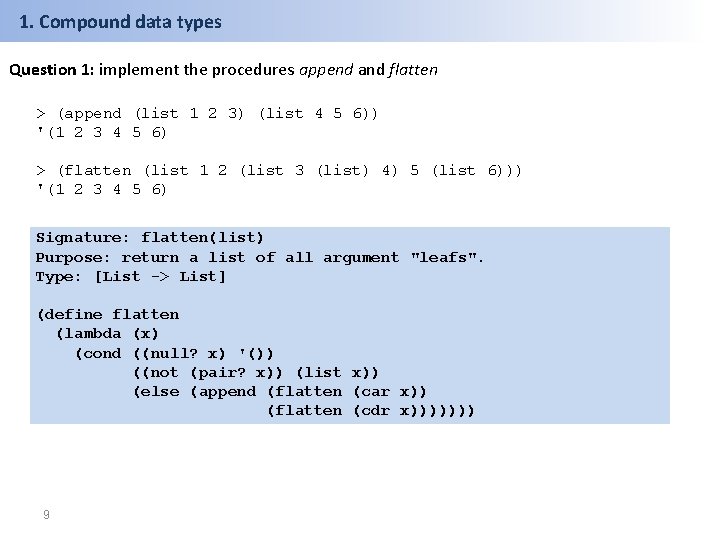
1. Compound data types Question 1: implement the procedures append and flatten > (append (list 1 2 3) (list 4 5 6)) '(1 2 3 4 5 6) > (flatten (list 1 2 (list 3 (list) 4) 5 (list 6))) '(1 2 3 4 5 6) Signature: append(list 1, list 2) Purpose: return a list which appends the arguments lists, from left to right. Type: [List * List -> List] (define append (lambda (x y) (if (null? x) y (cons (car x) (append (cdr x) y))))) 8

1. Compound data types Question 1: implement the procedures append and flatten > (append (list 1 2 3) (list 4 5 6)) '(1 2 3 4 5 6) > (flatten (list 1 2 (list 3 (list) 4) 5 (list 6))) '(1 2 3 4 5 6) Signature: flatten(list) Purpose: return a list of all argument "leafs". Type: [List -> List] (define flatten (lambda (x) (cond ((null? x) '()) ((not (pair? x)) (list x)) (else (append (flatten (car x)) (flatten (cdr x))))))) 9

2. Data abstraction: The ADT concept 2. Client Level (usage) 1. Abstract Data Types (ADTs): a. Data operators: constructors, selectors, predicates. b. Correctness rules (Invariants) 3. Supplier Level (implementation) 10

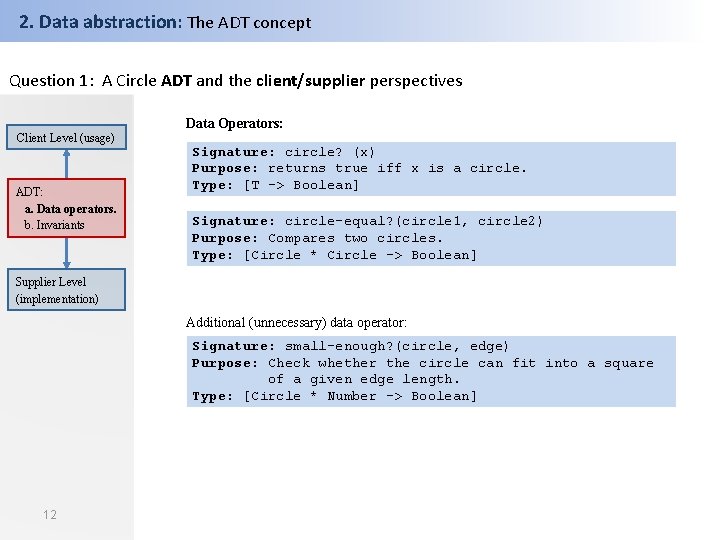
2. Data abstraction: The ADT concept Question 1: A Circle ADT and the client/supplier perspectives Data Operators: Client Level (usage) ADT: a. Data operators. b. Invariants Supplier Level (implementation) Signature: make-circle(x-center, y-center, radius) Purpose: constructs a circle. Type: [Number * Number -> Circle] Pre-conditions: radius >= 0 Signature: get-x-center(circle) Purpose: returns the x coordinate of the circle's center. Type: [Circle -> Number] Signature: get-y-center(circle) Purpose: returns the y coordinate of the circle's center. Type: [Circle -> Number] Signature: get-radius(circle) Purpose: returns the radius of the circle. Type: [Circle -> Number] 11

2. Data abstraction: The ADT concept Question 1: A Circle ADT and the client/supplier perspectives Data Operators: Client Level (usage) ADT: a. Data operators. b. Invariants Signature: circle? (x) Purpose: returns true iff x is a circle. Type: [T -> Boolean] Signature: circle-equal? (circle 1, circle 2) Purpose: Compares two circles. Type: [Circle * Circle -> Boolean] Supplier Level (implementation) Additional (unnecessary) data operator: Signature: small-enough? (circle, edge) Purpose: Check whether the circle can fit into a square of a given edge length. Type: [Circle * Number -> Boolean] 12

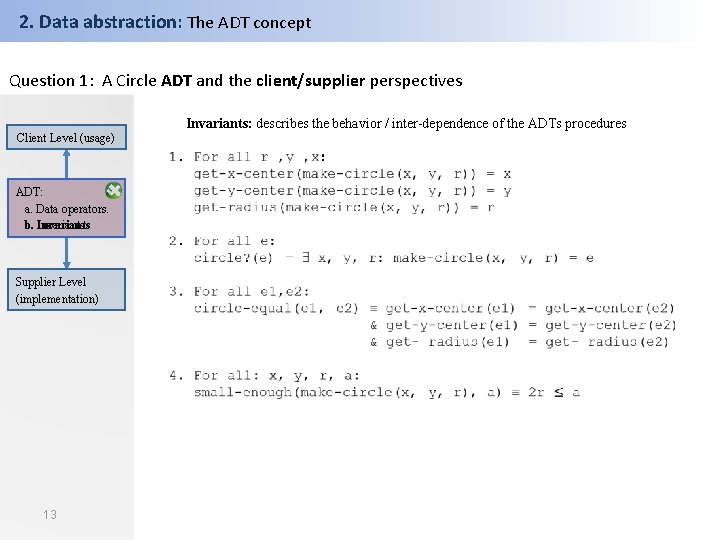
2. Data abstraction: The ADT concept Question 1: A Circle ADT and the client/supplier perspectives Invariants: describes the behavior / inter-dependence of the ADTs procedures Client Level (usage) ADT: a. Data operators. b. Invariants Supplier Level (implementation) 13

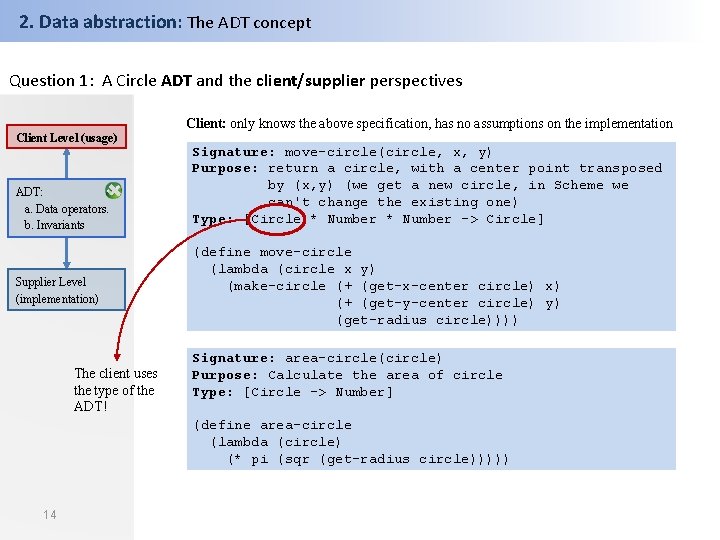
2. Data abstraction: The ADT concept Question 1: A Circle ADT and the client/supplier perspectives Client: only knows the above specification, has no assumptions on the implementation Client Level (usage) ADT: a. Data operators. b. Invariants Supplier Level (implementation) The client uses the type of the ADT! Signature: move-circle(circle, x, y) Purpose: return a circle, with a center point transposed by (x, y) (we get a new circle, in Scheme we can't change the existing one) Type: [Circle * Number -> Circle] (define move-circle (lambda (circle x y) (make-circle (+ (get-x-center circle) x) (+ (get-y-center circle) y) (get-radius circle)))) Signature: area-circle(circle) Purpose: Calculate the area of circle Type: [Circle -> Number] (define area-circle (lambda (circle) (* pi (sqr (get-radius circle))))) 14

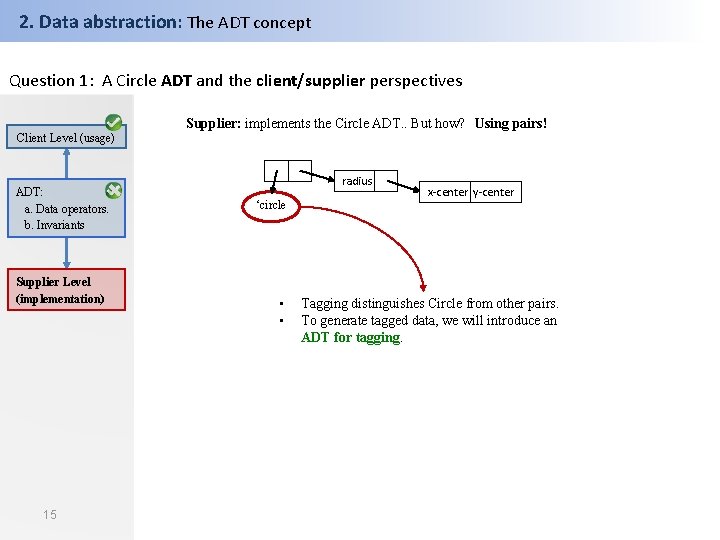
2. Data abstraction: The ADT concept Question 1: A Circle ADT and the client/supplier perspectives Supplier: implements the Circle ADT. . But how? Using pairs! Client Level (usage) ADT: a. Data operators. b. Invariants Supplier Level (implementation) 15 radius ‘circle • • x-center y-center Tagging distinguishes Circle from other pairs. To generate tagged data, we will introduce an ADT for tagging.

2. Data abstraction: The ADT concept Question 1: A Circle ADT and the client/supplier perspectives An ADT for tagging - Data Operators: Signature: attach-tag(x, tag) Purpose: Construct a tagged-data value Type: [T * Symbol -> Tagged-data(T)] Signature: get-tag(tagged) Purpose: Select the tag from a tagged-data value Type: [Tagged-data(T) -> Symbol] Signature: get-content(tagged) Purpose: Select the data from a tagged-data value Type: [Tagged-data(T) -> T] Signature: tagged-data? (datum) Purpose: Identify tagged-data values Type: [T -> Boolean] Signature: tagged-by? (tagged, tag) Purpose: Identify tagged-data values Type: [T * Symbol -> Boolean] 16

2. Data abstraction: The ADT concept Question 1: A Circle ADT and the client/supplier perspectives An ADT for tagging - implementation: (define attach-tag (lambda (x tag) (cons tag x))) (define get-tag (lambda (tagged) (car tagged))) (define get-content (lambda (tagged) (cdr tagged))) (define tagged-data? (lambda (datum) (and (pair? datum) (symbol? (car datum))))) (define tagged-by? (lambda (x tag) (and (tagged-data? x) (eq? (get-tag x) tag)))) 17

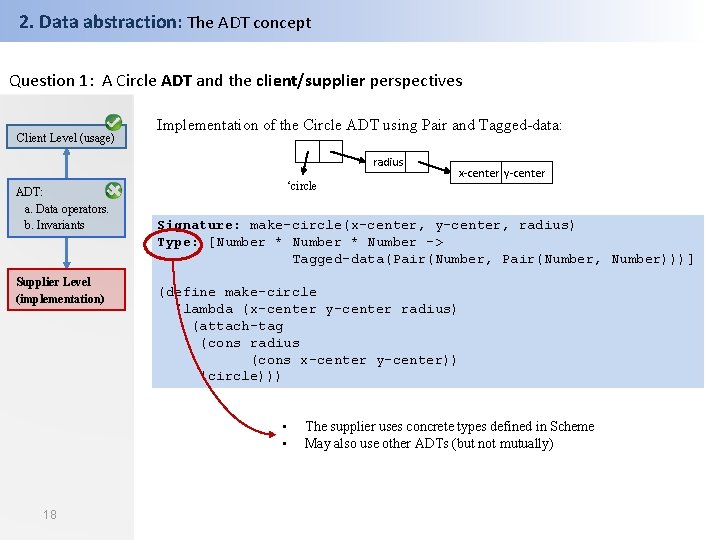
2. Data abstraction: The ADT concept Question 1: A Circle ADT and the client/supplier perspectives Client Level (usage) Implementation of the Circle ADT using Pair and Tagged-data: radius ADT: a. Data operators. b. Invariants Supplier Level (implementation) ‘circle Signature: make-circle(x-center, y-center, radius) Type: [Number * Number -> Tagged-data(Pair(Number, Number)))] (define make-circle (lambda (x-center y-center radius) (attach-tag (cons radius (cons x-center y-center)) 'circle))) • • 18 x-center y-center The supplier uses concrete types defined in Scheme May also use other ADTs (but not mutually)

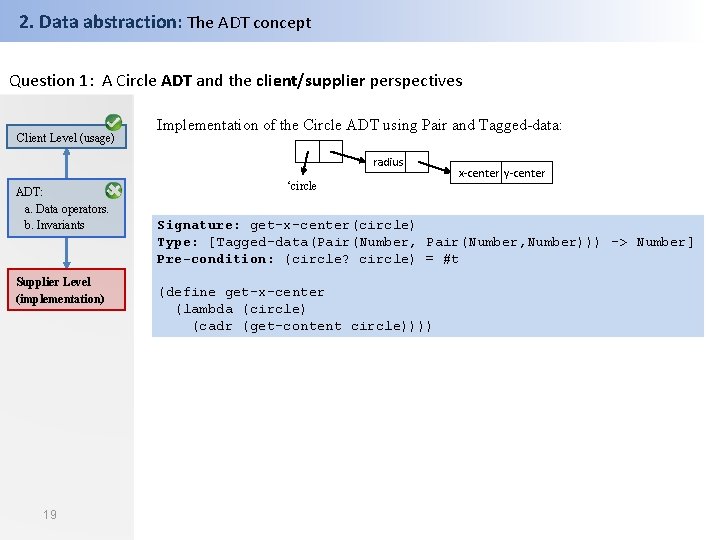
2. Data abstraction: The ADT concept Question 1: A Circle ADT and the client/supplier perspectives Client Level (usage) Implementation of the Circle ADT using Pair and Tagged-data: radius ADT: a. Data operators. b. Invariants Supplier Level (implementation) 19 ‘circle x-center y-center Signature: get-x-center(circle) Type: [Tagged-data(Pair(Number, Number))) -> Number] Pre-condition: (circle? circle) = #t (define get-x-center (lambda (circle) (cadr (get-content circle))))

2. Data abstraction: The ADT concept Question 1: A Circle ADT and the client/supplier perspectives Client Level (usage) Implementation of the Circle ADT using Pair and Tagged-data: radius ADT: a. Data operators. b. Invariants Supplier Level (implementation) 20 ‘circle Signature: circle? (object) Type: [T -> Boolean] (define circle? (lambda (circle) (tagged-by? circle 'circle))) x-center y-center

2. Data abstraction: The ADT concept Question 1: A Circle ADT and the client/supplier perspectives Client Level (usage) Implementation of the Circle ADT using Pair and Tagged-data: radius ADT: a. Data operators. b. Invariants Supplier Level (implementation) 21 ‘circle x-center y-center Signature: circle-equal? (circle 1, circle 2) Type: [Tagged-data(Pair(Number, Number)) * Tagged-data(Pair(Number, Number)))->Boolean] Pre-condition: (and (circle? circle 1) (circle? circle 2)) = #t (define circle-equal? (lambda (circle 1 circle 2) (and (= (get-x-center circle 1) (get-x-center circle 2)) (= (get-y-center circle 1) (get-y-center circle 2)) (= (get-radius circle 1) (get-radius circle 2)))))

2. Data abstraction: The ADT concept Question 1: A Circle ADT and the client/supplier perspectives Client Level (usage) Implementation of the Circle ADT using Pair and Tagged-data: radius ADT: a. Data operators. b. Invariants Supplier Level (implementation) 22 ‘circle x-center y-center Signature: small-enough? (circle, edge) Type: [Tagged-data(Pair(Number, Number))) * Number -> Boolean] Pre-condition: (circle? circle) = #t (define small-enough? (lambda (circle edge) (<= ((* 2 (get-radius circle)) edge))))

2. Data abstraction: The ADT concept Question 1: A Circle ADT and the client/supplier perspectives Client Level (usage) Proving the invariants (For example, the 3 rd invariant): get-radius(make-circle(x, y, r)) = r ADT: a. Data operators. b. Invariants Supplier Level (implementation) 23 Prove: For all x, y, r: applicative-eval[(get-radius (make-circle x y r)) ]==>* r Proof: For all x, y, r: applicative-eval[(get-radius (make-circle x y r))]==>* applicative-eval[(get-radius ('circle. (r. (x. y))))]==>* applicative-eval[(car (get-content ('circle. (r. (x. y)))))]==>* applicative-eval[(car (cdr ('circle. (r. (x. y)))))]==>* applicative-eval[(car (r. (x. y)))]==>* r.

3. Procedural implementation of ADTs Question 2: A Circle ADT - An eager procedural implementation Signature: make-circle(x-center, y-center, radius) Type: [Number * Number -> Tagged-data([Symbol -> Number])] (define make-circle (lambda (x-center y-center radius) (attach-tag (lambda (m) (cond ((eq? m 'x) x-center) ((eq? m 'y) y-center) (else radius))) 'circle)) Signature: get-x-center(circle) Type: [Tagged-data([Symbol -> Number]) -> Number] Pre-condition: (circle? circle) = #t (define get-x-center (lambda (circle) ((get-content circle) 'x))) Q: What about the remaining procedures declared in the ADT? Circle? , circle-equal? , small-enough? 24

3. Procedural implementation of ADTs Question 2: A Circle ADT - An eager procedural implementation Invariants proof: get-radius(make-circle(x, y, r)) = r Prove: For all x, y, r: applicative-eval[(get-radius (make-circle x y r)) ]==>* r Proof: For all x, y, r: a-e[(get-radius (make-circle x y r))]==>* a-e[(get-radius (attach-tag <closure(m) (cond ((eq? m 'x) x) ((eq? m 'y) y) (else r))> 'circle)))]==>* a-e[(get-radius (cons 'circle <closure(m) (cond ((eq? m 'x) x) ((eq? m 'y) y) (else r))>)] ==>* a-e[(<closure (m) (cond ((eq? m 'x) x) ((eq? m 'y) y) (else r))> 'r)] ==>* a-e[(cond ((eq? 'r 'x) x) ((eq? 'r 'y) y) (else r)) ] ==>* r 25

3. Procedural implementation of ADTs Question 3: A Circle ADT - A lazy procedural implementation Signature: make-circle(x-center, y-center, radius) Type: [N * N -> Tagged-data([[N * N -> T])] (define make-circle (lambda (x-center y-center radius) (attach-tag (lambda (sel) (sel x-center y-center radius)) 'circle))) Signature: get-x-center(circle) Type: [Tagged-data([Symbol -> Number]) -> Number] Pre-condition: (circle? circle) = #t (define get-x-center (lambda (circle) ((get-content circle) (lambda (x y r) x)))) 26

3. Procedural implementation of ADTs Question 3: A Circle ADT - A lazy procedural implementation Invariants proof: get-radius(make-circle(x, y, r)) = y Prove: For all x, y, r: applicative-eval[(get-radius (make-circle x y r)) ]==>* y Proof: For all x, y, r: a-e[(get-y-center (make-circle x y r))]==>* a-e[(get-y-center (attach-tag <closure(m) (sel x y r)> 'circle)))]==>* a-e[(get-y-center (cons 'circle <closure (sel) (sel x y r)>))] ==>* a-e[(<closure (circle) ((get-content circle) (lambda (x y r) y))> (cons 'circle <closure (sel) (sel x y r)>))] ==>* (renaming) a-e[(<closure (circle) ((get-content circle) (lambda (x 1 y 1 r 1) y 1))> (cons 'circle <closure (sel) (sel x y r)>))] ==>* r a-e[((get-content (cons 'circle <closure (sel) (sel x y r)>)) (lambda (x 1 y 1 r 1) y 1))] ==>* r a-e[(<closure (sel) (sel x y r)> <closure (x 1 y 1 r 1) y 1)>)] ==>* a-e[(<closure (x 1 y 1 r 1) y 1)> x y r) ] ==>* y 27

3. Procedural implementation of ADTs Summary: eager VS lazy procedural implementation (define make-circle (lambda (x-center y-center radius) (attach-tag (lambda (m) (cond ((eq? m 'x) x-center) ((eq? m 'y) y-center) (else radius))) 'circle)) (define make-circle (lambda (x-center y-center radius) (attach-tag (lambda (sel) (sel x-center y-center radius)) 'circle))) (define get-x-center (lambda (circle) ((get-content circle) 'x))) (define get-x-center (lambda (circle) ((get-content circle) (lambda (x y r) x)))) 28 • Lazy: the entire logic is at the selectors. Eager: the logic is at the constructor. • A lazy imp. may be easily extended compared with the eager one. • An eager imp. may be undesired when large amounts of instances are created.

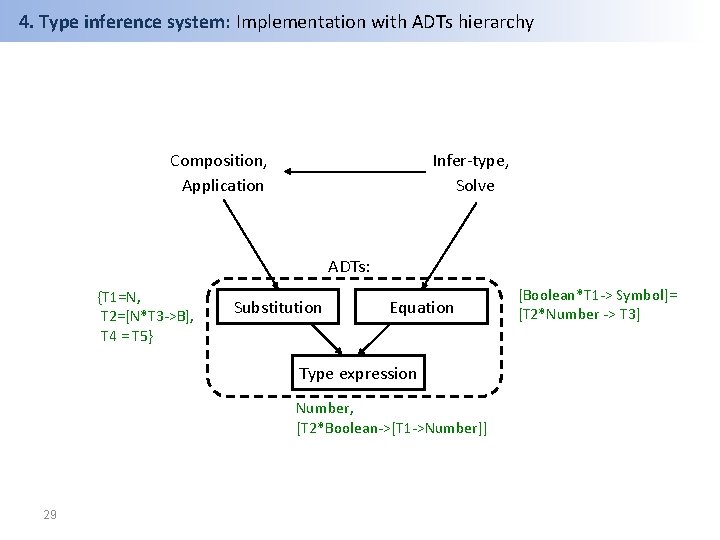
4. Type inference system: Implementation with ADTs hierarchy Composition, Application Infer-type, Solve ADTs: {T 1=N, T 2=[N*T 3 ->B], T 4 = T 5} Substitution Equation Type expression Number, [T 2*Boolean->[T 1 ->Number]] 29 [Boolean*T 1 -> Symbol]= [T 2*Number -> T 3]

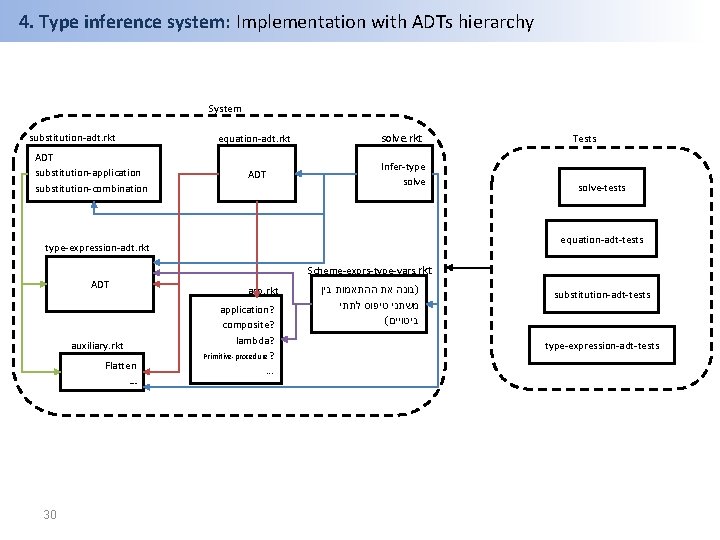
4. Type inference system: Implementation with ADTs hierarchy System substitution-adt. rkt ADT substitution-application substitution-combination equation-adt. rkt solve. rkt ADT Infer-type solve Tests solve-tests equation-adt-tests type-expression-adt. rkt Scheme-exprs-type-vars. rkt ADT auxiliary. rkt Flatten … 30 asp. rkt application? composite? lambda? Primitive-procedure ? . . . בין ההתאמות את )בונה לתתי טיפוס משתני ( ביטויים substitution-adt-tests type-expression-adt-tests

4. Type inference system: Implementation with ADTs hierarchy Selected parts of the Substitution ADT – Constructor: Signature: make-sub(variables, tes) Purpose: Create a substitution in which the i-th element of 'variables' is mapped to the i-th element of 'tes'. Type: [List(Symbol)*List(Type-expression) -> Substitution] Examples: a. (make-sub '(x y z) (list 'Number 'Boolean (make-proc-te (make-tuple-te (list 'Number)) 'Number))) ==> ((x y z) (Number Boolean (-> (* Number))) b. (make-sub '(x y z) (list 'Number 'Boolean (make-proc-te (make-tuple-te (list 'z)) 'Number))) ==> make-sub: circular substitution: ((x y z) (Number Boolean (-> (* z) Number))) Pre-condition: (length variables) = (length tes) 31

4. Type inference system: Implementation with ADTs hierarchy Selected parts of the Substitution ADT – Predicates: Signature: empty-sub? (sub) Type: [T -> Boolean] Examples: a. (empty-sub? (make-sub '(x y z) (list 'Number 'Boolean (make-proc-te (make-tuple-te (list 'Number)) 'Number)))) ==> #f b. (empty-sub? (make-sub (list))) ==> #t 32

4. Type inference system: Implementation with ADTs hierarchy Selected parts of the Substitution ADT – Selectors: Signature: get-variables(sub) Type: [substitution -> List(Var)] Example: (get-variables (make-sub '(x y z) (list 'Number 'Boolean (make-proc-te (make-tuple-te (list 'Number)) 'Number)))) ==> (x y z) Signature: get-tes(sub) Type: [substitution -> List(TE)] Example: (get-tes (make-sub '(x y z) (list 'Number 'Boolean (make-proc-te (make-tuple-te (list 'Number)) 'Number)))) ==> (Number Boolean (-> (* Number)) 33

4. Type inference system: Implementation with ADTs hierarchy Selected parts of the Substitution ADT – Auxiliary procedures: Signature: extend-sub(sub, var, te) Type: [substitution * var * TE -> substitution] Examples: (extend-sub (make-sub '(T 1 T 2 T 3) (list 'S 1 (make-tuple-te (list 'S 2 'Number)) 'Boolean)) 'S 1 (make-tuple-te (list 'T 4 (make-proc-te (make-tuple-te (list 'Number 'T 5)) 'T 6)))) ==> '((S 1 T 2 T 3) ((* T 4 (-> (* Number T 5) T 6)) (* S 2 Number) Boolean)) {T 1=S 1, T 2=(S 2 * Number), T 3 = Boolean} ==> {S 1=(* T 4 (-> (* Number T 5) T 6) ), T 2=(S 2 * Number), T 3 = Boolean} 34

4. Type inference system: Implementation with ADTs hierarchy Usage of the Substitution ADT – the procedure substitution-combination: Recall the steps in combining two substitutions, S and S’: S = {S 1=Number, S 2=[Number*Number->[T 1 ->Number]], S 3= T 3]} S‘ = {T 1=Boolean, T 2=Symbol, S 3=Number} According to the following steps: 1. S’ is applied to type-expressions of S 2. Any variables T for which S(T) is defined is removed from S’ 3. The modified S’ is added to S. 4. Identity bindings T=S(T) are removed. We get: S o S’ = {S 1=Number, S 2=[Number*Number->[Boolean->Number]], S 3= T 3, T 1=Boolean, T 2=Symbol]} 35

4. Type inference system: Implementation with ADTs hierarchy Usage of the Substitution ADT – the procedure substitution-combination: Signature: substitution-combination(sub 1, sub 2) Type: [Substitution*Substitution -> Substitution] Example: (substitution-combination (make-sub '(T 1 T 2 T 3) (list 'S 1 (make-tuple-te (list 'S 2 'Number)) 'Boolean)) (make-sub '(S 1 S 2) (list (make-tuple-te (list 'T 4 (make-proc-te (make-tuple-te (list 'Number 'T 5)) 'T 5))) 'T 3))) ==> ((S 2 S 1 T 2 T 3) (T 3 (* T 4 (-> (* Number T 5)) (* T 3 Number) Boolean)) {T 1=S 1, T 2=(* S 2 Number), T 3 = Boolean} o {S 1=(* T 4 (-> (* Number T 5) ), S 2=T 3} 36

4. Type inference system: Implementation with ADTs hierarchy Usage of the Substitution ADT – the procedure substitution-combination: (define substitution-combination (lambda (sub 1 sub 2) (cond ((empty-sub? sub 1) sub 2) ((empty-sub? sub 2) sub 1) (else (letrec ((combine (lambda (sub vars tes) (if (empty? vars) sub (combine (extend-sub (car vars) (car tes)) (cdr vars) (cdr tes)))))) (combine sub 1 (get-variables sub 2) (get-tes sub 2))))) )) Q: Where in the implementation above circularity must be handled? 37