Practical Mobility Models Mobility Based Routing Joy Ghosh

Practical Mobility Models & Mobility Based Routing Joy Ghosh LANDER cse@buffalo

Outline n n n n Impact of mobility on protocol performance Pros & Cons of Random Waypoint model Entity, Group & Scenario based models Our proposed ORBIT mobility framework Our proposed Orbit Based Routing schemes Future direction Conclusion
Impact of mobility on protocol performance n F. Bai, N. Sadagopan, and A. Helmy, “Important: a framework to systematically analyze the impact of mobility on performance of routing protocols for adhoc networks”, Proceedings of IEEE INFOCOM '03, vol. 2, pp. 825 -835, March 2003.

Random Waypoint mobility model n Parameters q q q n Pause time = p Max velocity = vmax Min velocity = vmin Description q q q Pick a random point within terrain Select a velocity vi such that vmin ≤ vi ≤ vmax Move linearly with velocity vi towards the chosen point On reaching the destination, pause for specified time p Repeat the steps above for entire simulation

Random Waypoint mobility model n Pros q q n Simple to implement Easy theoretical analysis Cons q q Highly impractical in real world networks Average speed decay problem n n Long journeys at low speeds Solution – use non-zero min speed!

Examples of entity based mobility n Random Walk Mobility Model (including its many derivatives) q n Random Waypoint Mobility Model q n A model that uses one tuning parameter to vary the degree of randomness in the mobility pattern. A Probabilistic Version of the Random Walk Mobility Model q n A model that converts a 2 D rectangular simulation area into a torus-shaped simulation area. Gauss-Markov Mobility Model q n A model that forces MNs to travel to the edge of the simulation area before changing direction and speed. A Boundless Simulation Area Mobility Model q n A model that includes pause times between changes in destination and speed. Random Direction Mobility Model q n A simple mobility model based on random directions and speeds. A model that utilizes a set of probabilities to determine the next MN position. City Section Mobility Model q A simulation area that represents streets within a city.

Examples of group based mobility n n n Exponential Correlated Random Mobility Model q A group mobility model that uses a motion function to create movements. Column Mobility Model q A group mobility model where the set of MNs form a line and are uniformly moving forward in a particular direction. Nomadic Community Mobility Model q A group mobility model where a set of MNs move together from one location to another. Pursue Mobility Model q A group mobility model where a set of MNs follow a given target. Reference Point Group Mobility Model q A group mobility model where group movements are based upon the path traveled by a logical center.
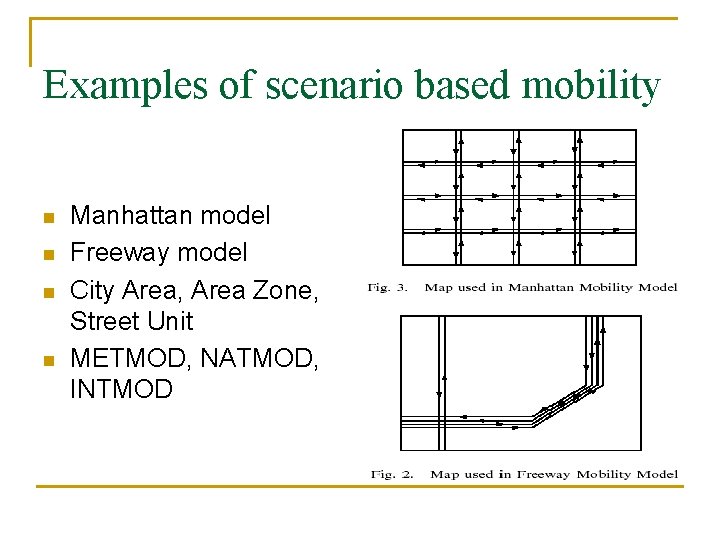
Examples of scenario based mobility n n Manhattan model Freeway model City Area, Area Zone, Street Unit METMOD, NATMOD, INTMOD

Outline n n n n Impact of mobility on protocol performance Pros & Cons of Random Waypoint model Entity, Group & Scenario based models Our proposed ORBIT mobility framework Our proposed Orbit Based Routing schemes Future direction Conclusion

Sociological Orbits Porch Home Y A R d Kitchen City 2: Relatives Mall / Plaza Outdoors City 1: Home Town Restaurant Cubicle Work Rest room City 3: Friends Cafeteria Level 0 Orbit Area Level 1 Orbit Path Level 2 Orbit Path Level 3 Orbit Path
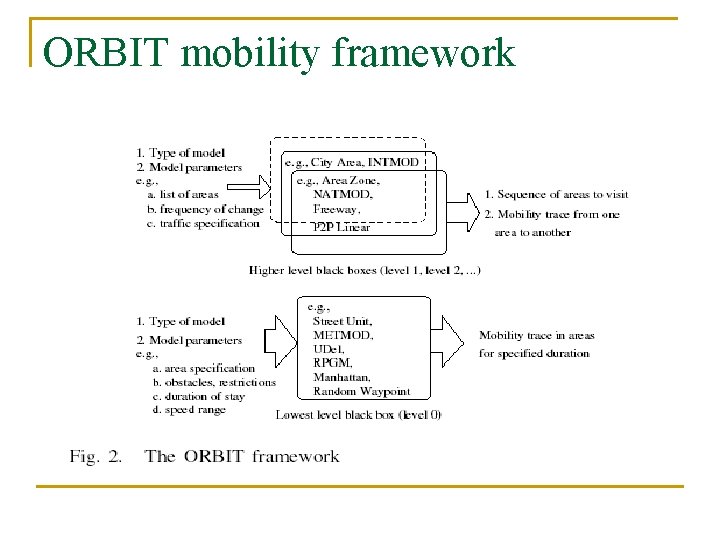
ORBIT mobility framework
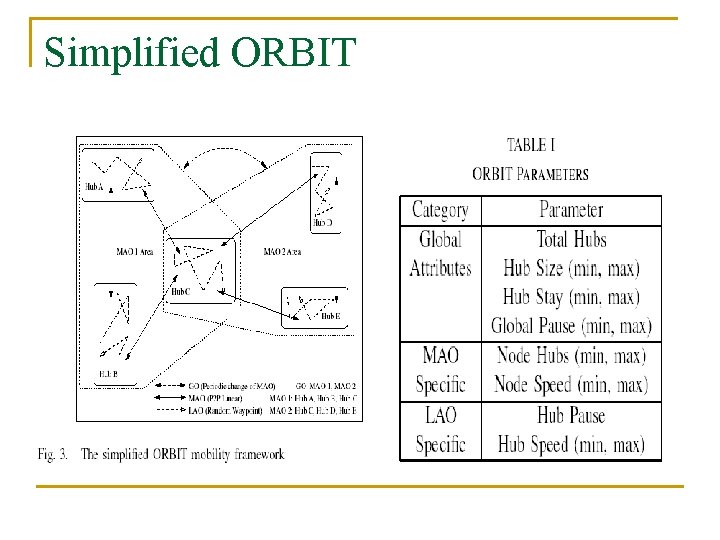
Simplified ORBIT
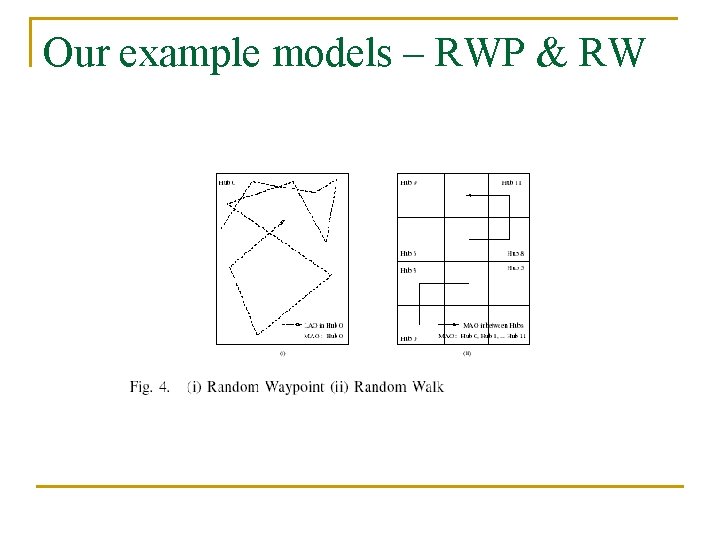
Our example models – RWP & RW
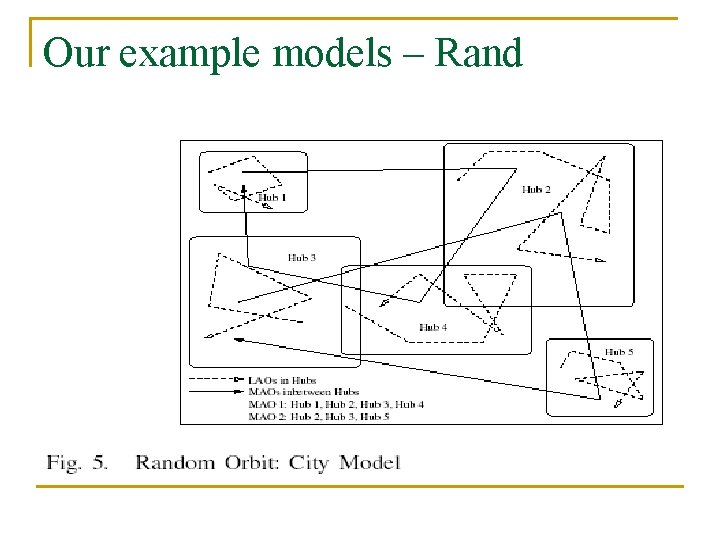
Our example models – Rand
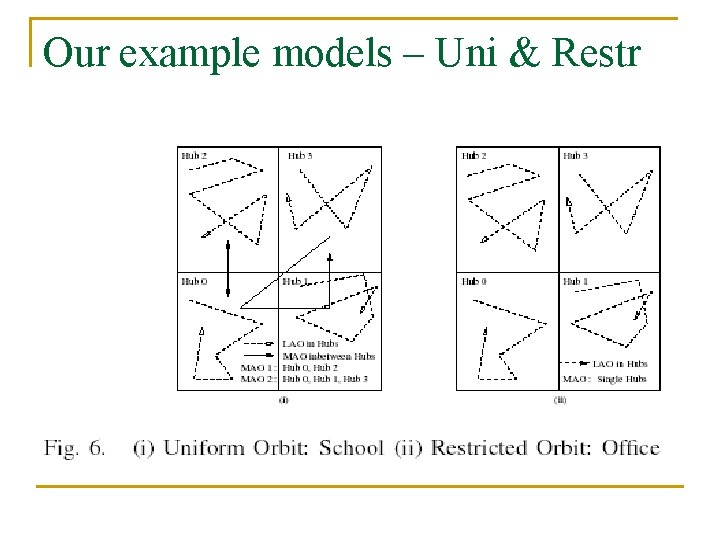
Our example models – Uni & Restr

Our example models - Ovly
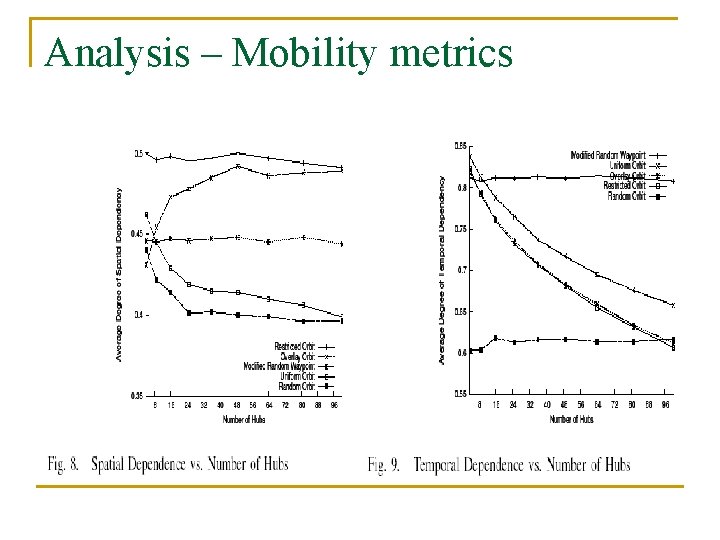
Analysis – Mobility metrics
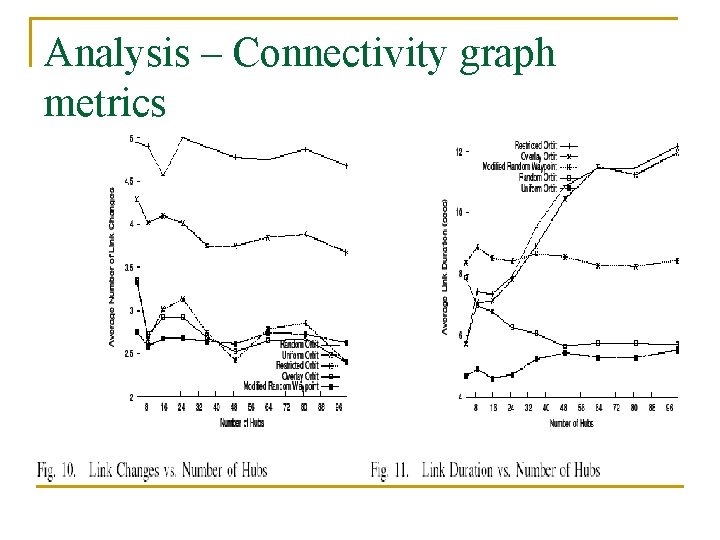
Analysis – Connectivity graph metrics

Outline n n n n Impact of mobility on protocol performance Pros & Cons of Random Waypoint model Entity, Group & Scenario based models Our proposed ORBIT mobility framework Our proposed Orbit Based Routing schemes Future direction Conclusion

Orbit Based Routing - Basics n n n Each node is assumed to know their own coordinates and the coordinates of the Hubs in the terrain Get acquainted with neighbors Share (own)/ Cache (other’s) Hub list information Build a distributed database of Hub lists Query acquaintances, and acquaintances of acquaintances, and so on for unknown MNs
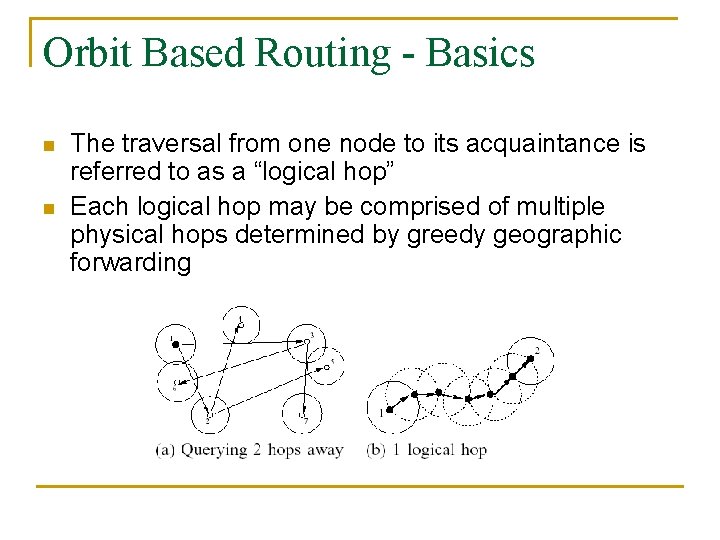
Orbit Based Routing - Basics n n The traversal from one node to its acquaintance is referred to as a “logical hop” Each logical hop may be comprised of multiple physical hops determined by greedy geographic forwarding

Information Query & Response n No Hub list information exists for destination q q q A subset of acquaintances is chosen (as explained later) and a query packet is sent to the Hub list of each of these acquaintances (as also explained later) If an acquaintance has no information, it can forward the query packet to a subset of its own acquaintances – unless the logical hop of the packet has exceeded a specified threshold Intermediate nodes can respond if appropriate

Subset of acquaintances to query n Problem q n Solution q n n n n Lots of acquaintances lot of query overhead Query a subset such that all the Hubs that a node learns of from its acquaintances are covered Let H 1, H 2, …, Hn be the Hub lists of acquaintances A 1, A 2, …, An Let H = {H 1, H 2, …, Hn} // collection of all sets of Hubs Let C be the collection of all Hubs known through sets in H Hence, C = U {H 1, H 2, …, Hn} Objective is to find a minimum subset This is a minimum set cover problem – NP Complete We use the Quine-Mc. Cluskey optimization technique

Quine-Mc. Cluskey optimization n Node A with Hub list Hj is a Prime acquaintance iff: n n Let P be the set of all Prime acquaintances Prime acquaintance A with Hub list Hj will be an Essential Prime acquaintance iff: n Example: A = {1, 2}, B = {2, 3, 4}, C = {1, 3} q q n n A is a Prime acquaintance B is an Essential Prime acquaintance Choose all the Essential Prime acquaintances first If any Hub is still uncovered, iteratively choose non-essential Prime acquaintances that cover the max number of remaining Hubs, till all Hubs are covered

Packet Transmission to Hub lists n Key concept of OBR q q q Associate node location information with Hub lists Send all types of packets to a node by transmitting to its Hub list Several possible ways different OBR Schemes
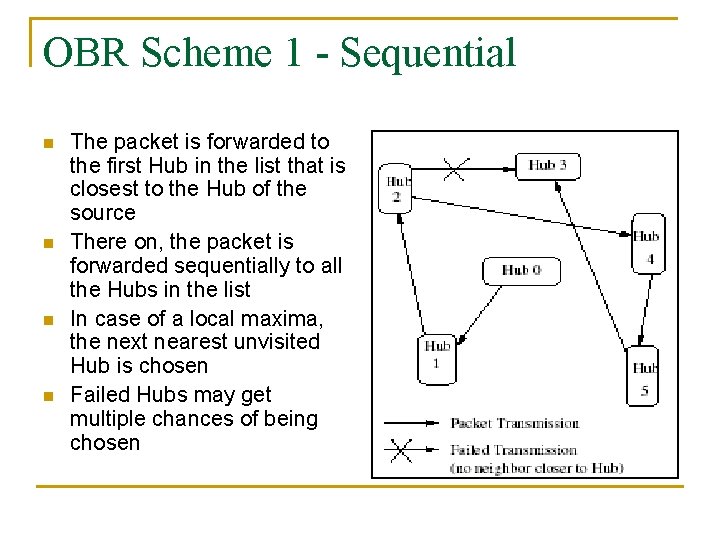
OBR Scheme 1 - Sequential n n The packet is forwarded to the first Hub in the list that is closest to the Hub of the source There on, the packet is forwarded sequentially to all the Hubs in the list In case of a local maxima, the next nearest unvisited Hub is chosen Failed Hubs may get multiple chances of being chosen
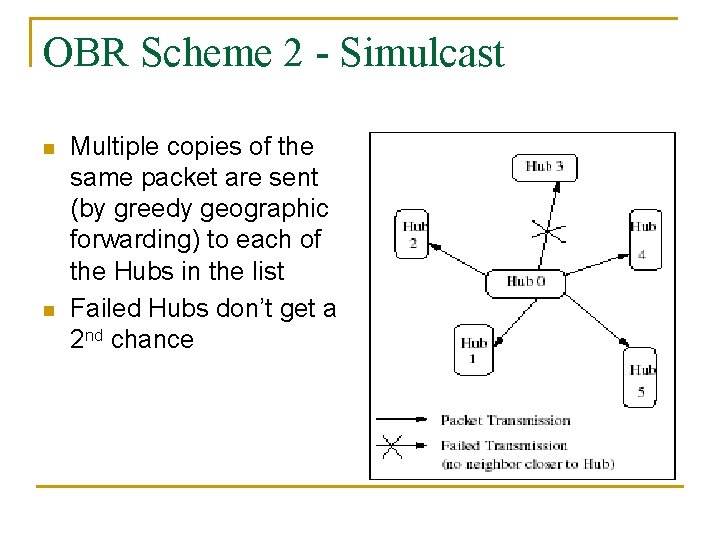
OBR Scheme 2 - Simulcast n n Multiple copies of the same packet are sent (by greedy geographic forwarding) to each of the Hubs in the list Failed Hubs don’t get a 2 nd chance
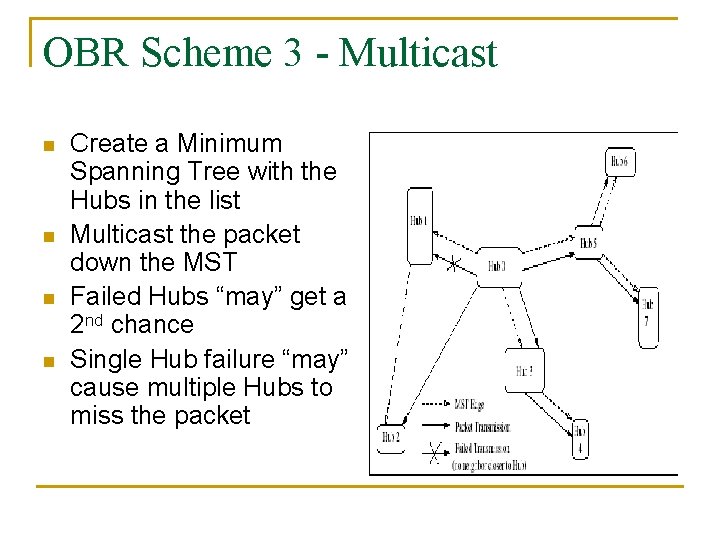
OBR Scheme 3 - Multicast n n Create a Minimum Spanning Tree with the Hubs in the list Multicast the packet down the MST Failed Hubs “may” get a 2 nd chance Single Hub failure “may” cause multiple Hubs to miss the packet

OBR – connection maintenance n n n In every data packet, source puts its current Hub information While session is active, if destination changes Hub, it updates the source Such data and update packets use the current Hub information to reduce delay

Acquaintance Based Soft Location Management (ABSo. Lo. M) n n Our prior work OBR is conceptually same In ABSo. Lo. M, nodes make limited acquaintances and kept track of their exact coordinates via regular updates The logical hops for a query were limited too We had obtained high throughput with very low control overhead

Performance Analysis Parameters n n n n Simulations in Glo. Mo. Sim 100 nodes in 1000 m x 1000 m for 1000 sec Radio range of 250 m 150 random CBR connections Each connection sends 10 packets (512 b) LAO Speed (min, max) = 1 m/s, 10 m/s MAO Speed (min, max) = 10 m/s, 30 m/s
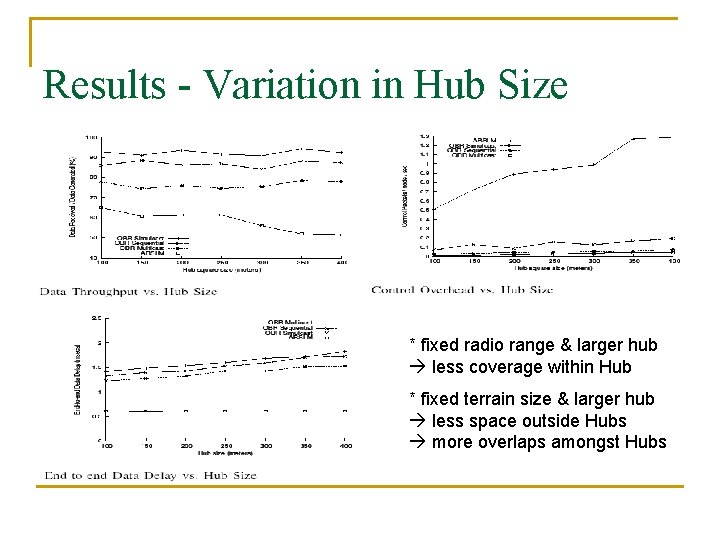
Results - Variation in Hub Size * fixed radio range & larger hub less coverage within Hub * fixed terrain size & larger hub less space outside Hubs more overlaps amongst Hubs
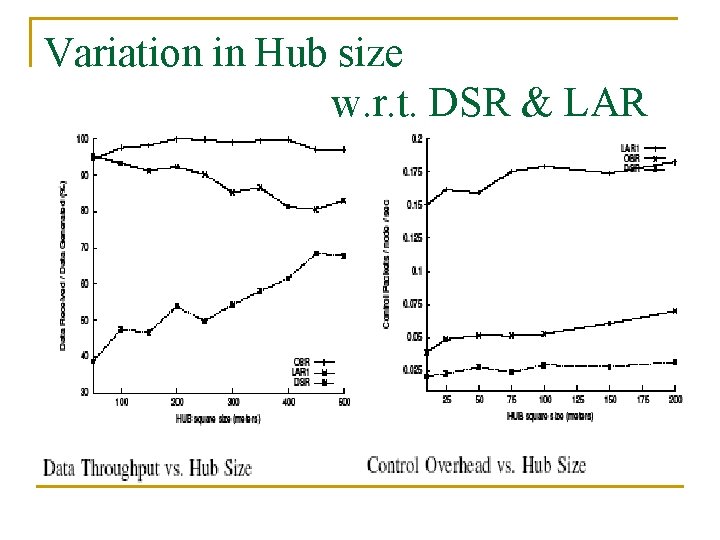
Variation in Hub size w. r. t. DSR & LAR

Results – Variation in LAO Timeout * lower LAO timeout higher avg. node velocity in MAO * higher LAO timeout higher avg. node population in Hubs
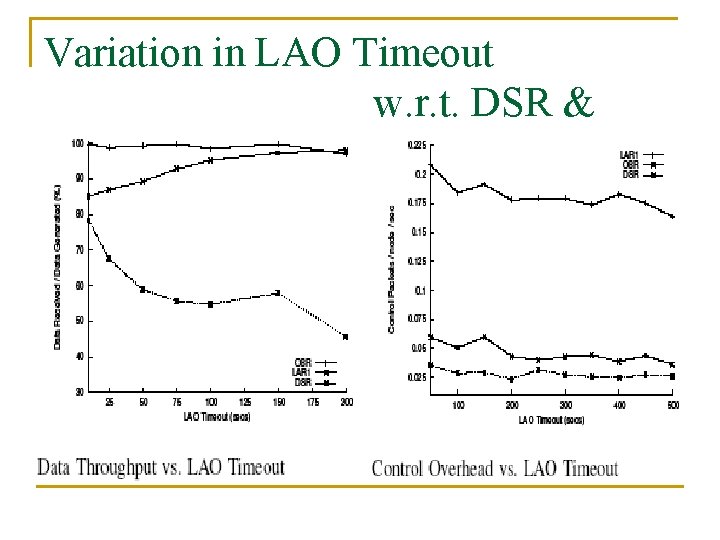
Variation in LAO Timeout w. r. t. DSR & LAR
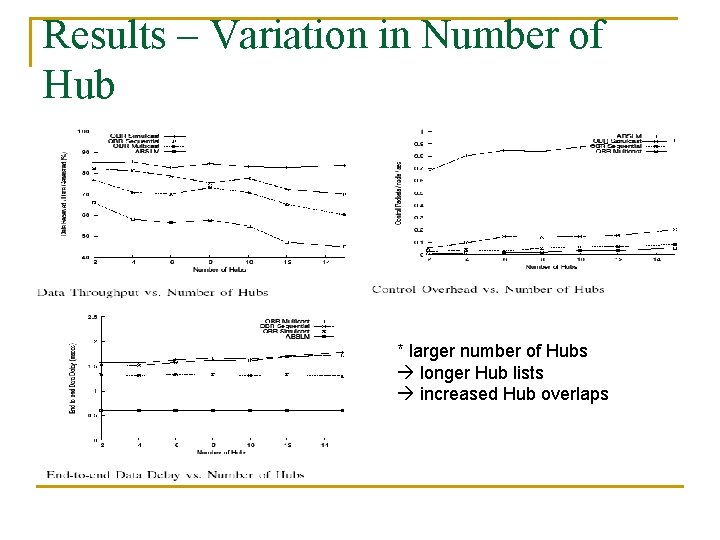
Results – Variation in Number of Hub * larger number of Hubs longer Hub lists increased Hub overlaps

Outline n n n n Impact of mobility on protocol performance Pros & Cons of Random Waypoint model Entity, Group & Scenario based models Our proposed ORBIT mobility framework Our proposed Orbit Based Routing schemes Future direction Conclusion

Future direction n Micro level mobility aided routing q n Delay Tolerant Networks q q n Mobility prediction Packet traversal may involve both packet transmission and carrying the packet physically Actually makes use of mobility in a practical way Space communications q Inter. Pla. Netary Internet

Conclusion n n Random Waypoint - of theoretical interest Several mobility models – ORBIT provides a generic framework OBR – first direct attempt to route based on mobility information Combining packet transmission with node mobility may prove useful for DTNs Applications in Space communications

References (mostly for the figures) n n n F. Bai, N. Sadagopan, and A. Helmy, “Important: a framework to systematically analyze the impact of mobility on performance of routing protocols for adhoc networks”, Proceedings of IEEE INFOCOM '03, vol. 2, pp. 825 -835, March 2003. T. Camp, J. Boleng, and V. Davies, “A Survey of Mobility Models for Ad Hoc Network Research”, Wireless Communications and Mobile Computing (WCMC): Special issue on Mobile Ad Hoc Networking: Research, Trends and Applications, vol. 2, no. 5, pp. 483 -502, 2002. J. Ghosh, S. J. Philip, and C. Qiao, “Acquaintance Based Soft Location Management (ABSLM) in MANET”, Proceedings of IEEE Wireless Communications and Networking Conference (WCNC) '04, March 2004. J. Ghosh, S. J. Philip, and C. Qiao, “ORBIT Mobility Framework and Orbit Based Routing (OBR) Protocol for MANET”, CSE Dept. TR # 2004 -08, State University of New York at Buffalo, 2004 (July) I. F. Akyildiz, O. B. Akan, C. Chen, J. Fang, W. Su, “Inter. Pla. Netary Internet: state-ofthe-art and research challenges” – Elsevier Computer Networks Journal (to appear) S. Jain, K. Fall, R. Patra, “Routing in a Delay Tolerant Network” – Proceedings of ACM SIGCOMM ’ 04, August, 2004
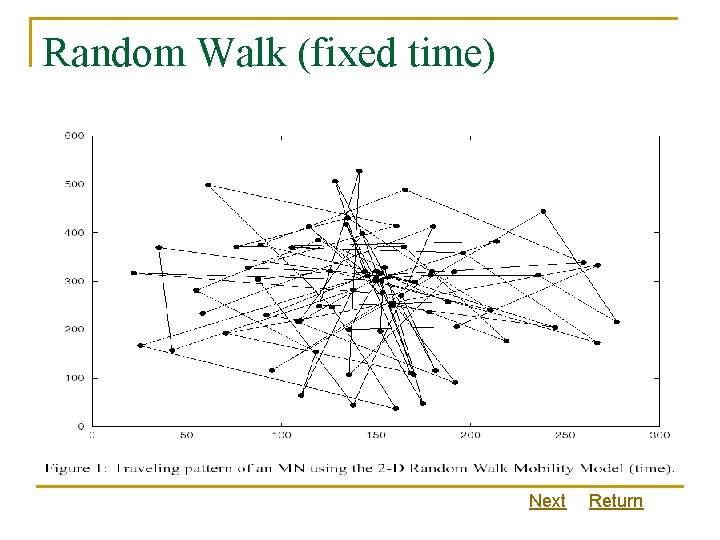
Random Walk (fixed time) Next Return
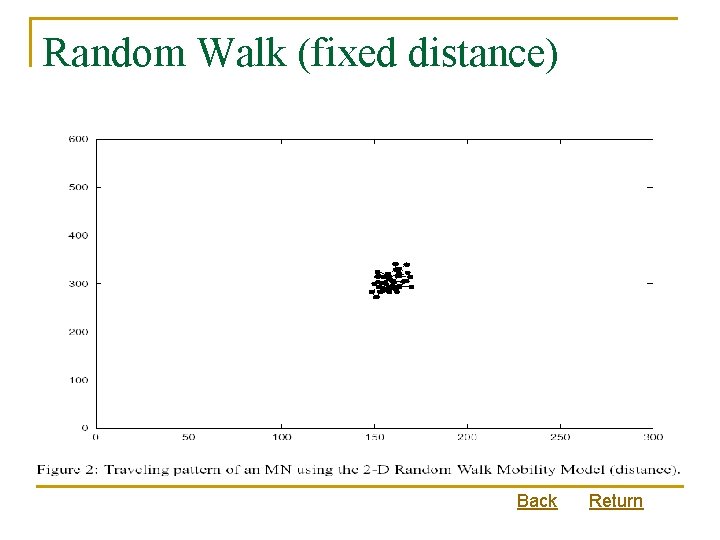
Random Walk (fixed distance) Back Return

Random Waypoint Return

Random Direction Return
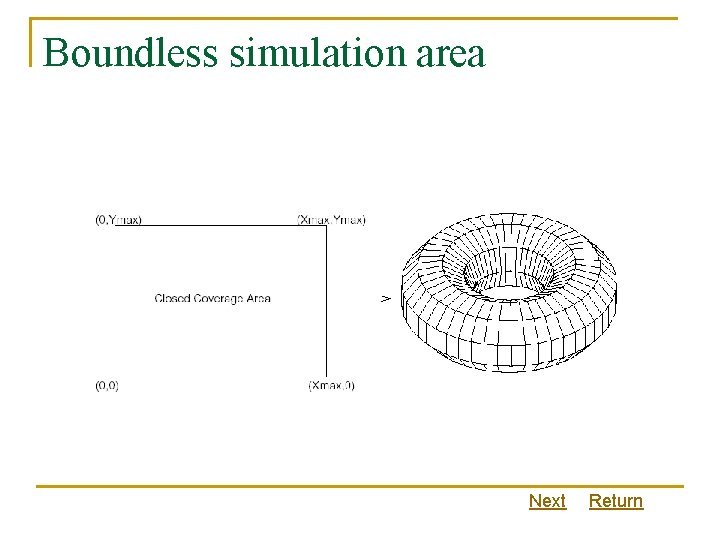
Boundless simulation area Next Return

Boundless simulation area mobility Back Return

Gauss-Markov (α: randomness factor) Return

Probabilistic Random Walk Return

City Section Return
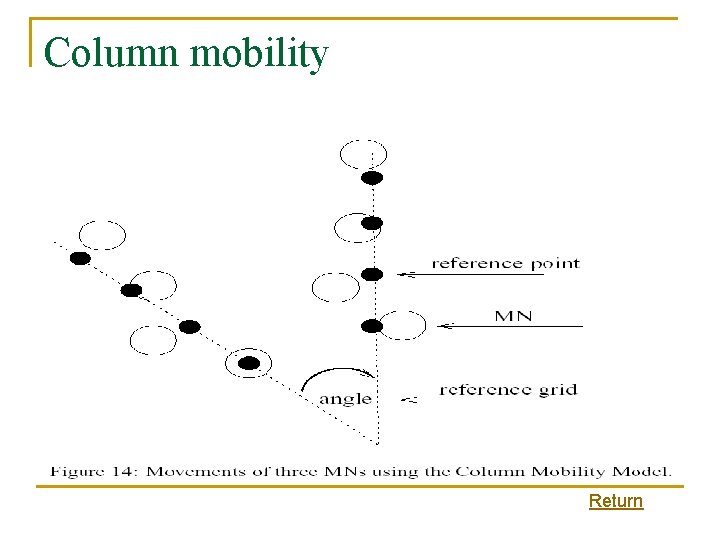
Column mobility Return
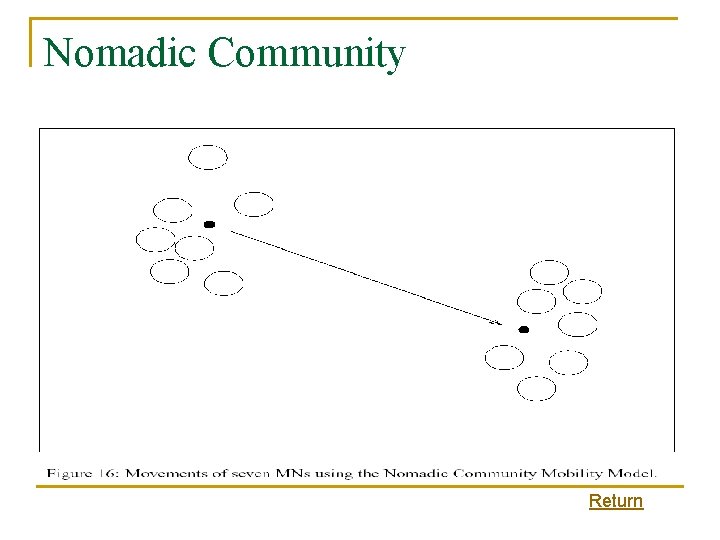
Nomadic Community Return

Pursue mobility Return
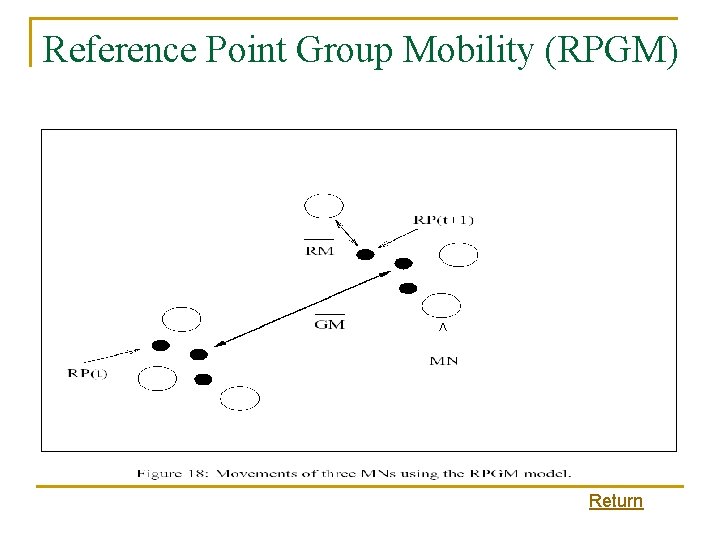
Reference Point Group Mobility (RPGM) Return
- Slides: 53