Practical Application of Doseresponse Functions in Weed Science
































- Slides: 60

Practical Application of Dose-response Functions in Weed Science William J. Price Statistical Programs College of Agricultural and Life Sciences University of Idaho, Moscow, Idaho

• Statistical Estimation Software • SAS • S+ • R • Statistica, etc. • Sigma Plot, AXUM, etc.

Common Dose-response Models • Normal: yij = (1/ 2 ) exp((x- )2/ 2 • Logistic: yij = 1 / (1 + exp( -b 1( dosei - b 0 )) • Modified Logistic: yij = C + (D-C) / (1 + exp( -B(dosei - I))) (e. g. Seefeldt et al. 1995) • Gompertz: • Exponential: yij = b 0 (1 - exp(-b 1(dose)))) yij = b 0 exp(-b 1(dose)) yij = b 0 [1 - exp(-b 1(dose))]

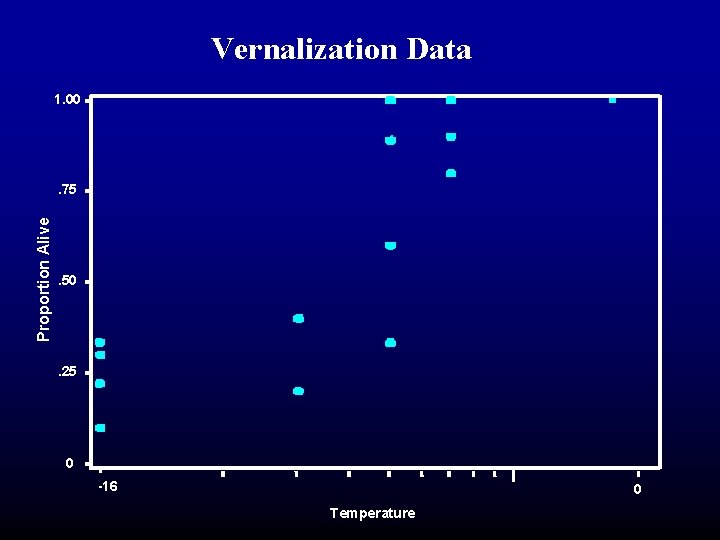
Probit Maximum Likelihood • Data description • Vernalization study. • Fixed number of wheat plants • 6 to 10 wheat plants per replication and temperature. • (SAS: plants). • Five temperatures (doses): • 0, -12, -14, and -16 degrees celcius • (SAS: temp = temperature + 17). • Number of wheat plants alive after 2 weeks recorded • (SAS: alive 2 wk).

Vernalization Data 1. 00 Proportion Alive . 75 . 50 . 25 0 -16 0 Temperature

Probit Maximum Likelihood • SAS Procedure: PROC PROBIT. • Code: proc lackfit inversecl; proc probitdata=freezelog logoptc lackfit inversecl; model alive 2 wk/plants = temp/distribution=logistic ; predpplotvar=temp; predpplot

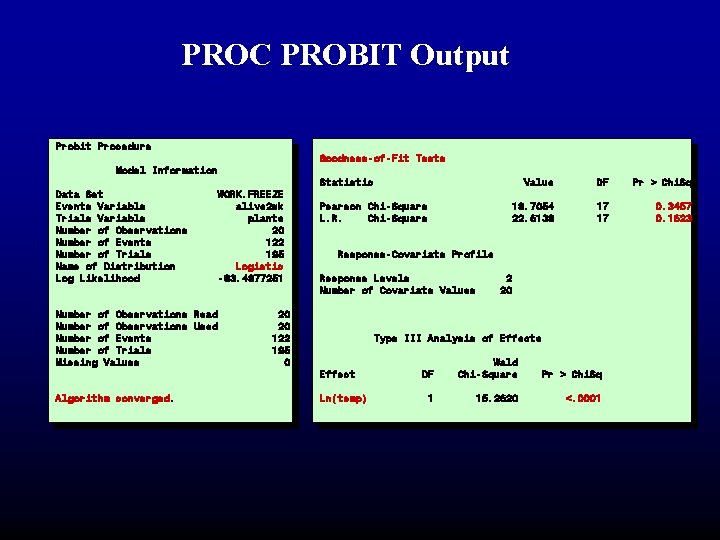
PROC PROBIT Output Probit Procedure Goodness-of-Fit Tests Model Information Data Set Events Variable Trials Variable Number of Observations Number of Events Number of Trials Name of Distribution Log Likelihood Number of Observations Read Number of Observations Used Number of Events Number of Trials Missing Values WORK. FREEZE alive 2 wk plants 20 122 195 Logistic -83. 4877251 Algorithm converged. 20 20 122 195 0 Statistic Pearson Chi-Square L. R. Chi-Square Value DF Pr > Chi. Sq 18. 7054 22. 6138 17 17 0. 3457 0. 1623 Response-Covariate Profile Response Levels Number of Covariate Values 2 20 Type III Analysis of Effects Effect Ln(temp) DF Wald Chi-Square Pr > Chi. Sq 1 15. 2620 <. 0001

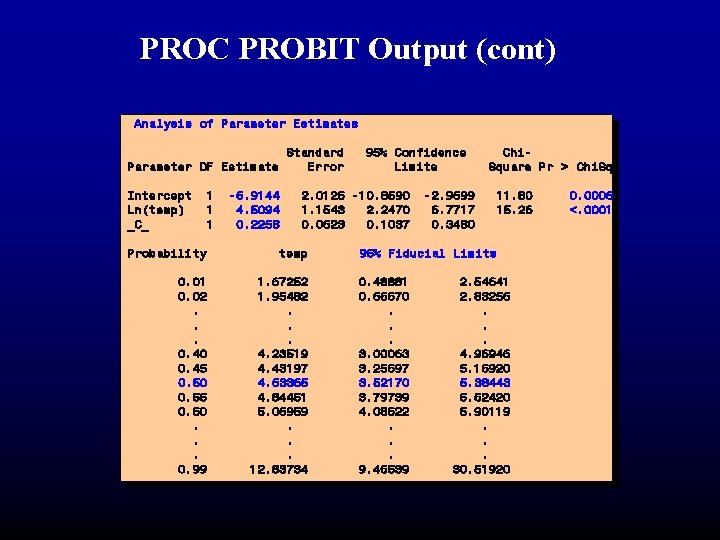
PROC PROBIT Output (cont) Analysis of Parameter Estimates Standard Error Parameter DF Estimate Intercept Ln(temp) _C_ 1 1 1 -6. 9144 4. 5094 0. 2258 95% Confidence Limits 2. 0126 -10. 8590 1. 1543 2. 2470 0. 0623 0. 1037 Probability temp 0. 01 0. 02. . . 0. 40 0. 45 0. 50 0. 55 0. 60. . . 0. 99 1. 67252 1. 95482. . . 4. 23519 4. 43197 4. 63365 4. 84451 5. 06959. . . 12. 83734 -2. 9699 6. 7717 0. 3480 Chi. Square Pr > Chi. Sq 11. 80 15. 26 95% Fiducial Limits 0. 48881 0. 66670. . . 3. 00063 3. 25697 3. 52170 3. 79739 4. 08622. . . 9. 46539 2. 54641 2. 83256. . . 4. 96946 5. 16920 5. 38443 5. 62420 5. 90119. . . 30. 51920 0. 0006 <. 0001

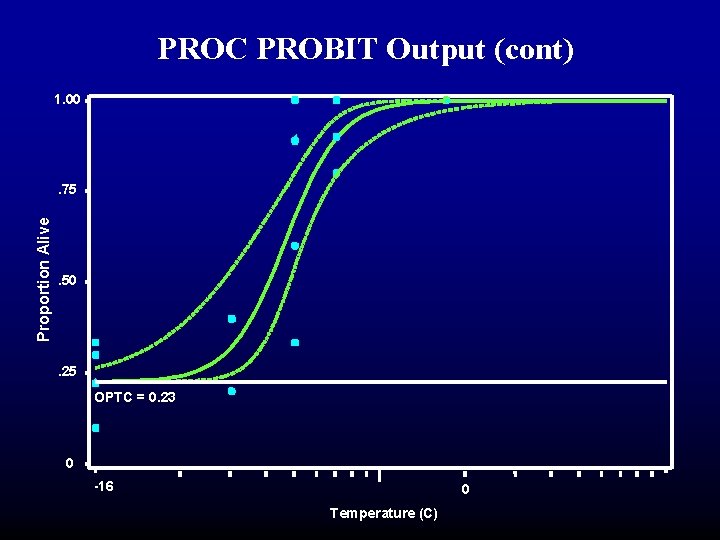
PROC PROBIT Output (cont) 1. 00 Proportion Alive . 75 . 50 . 25 OPTC = 0. 23 0 -16 0 Temperature (C)

PROC PROBIT (cont) • Probit Advantages • • Automatic Goodness of Fit test. Easily computed percentiles. Ability to do treatment comparisons. Graphic output. • Probit Limitations • Proportional Data. • Maximum set to 1. 0. • Limited number of response models.

Nonlinear Least Squares • SAS Procedure: PROC NLIN • Code: proc nlindata=freeze; ; parms. I I= =8 8 B = B -4. 5 =. 12; parms C = C. 12; bounds. B<0; mu == CC ++(1 -C)/(1 + exp(B*(ltemp-log(I)))); mu + exp(B*(ltemp-log(I)))); model per 2= =mu; output out=predp=pred;

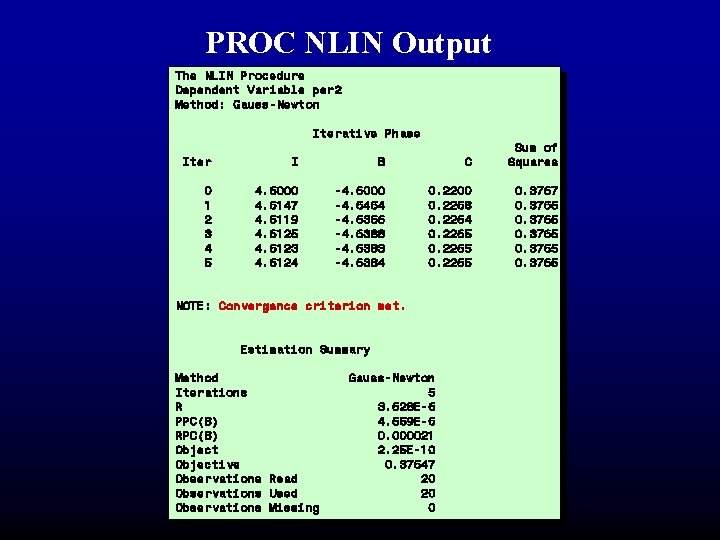
PROC NLIN Output The NLIN Procedure Dependent Variable per 2 Method: Gauss-Newton Iterative Phase Iter I B C Sum of Squares 0 1 2 3 4 5 4. 6000 4. 6147 4. 6119 4. 6125 4. 6123 4. 6124 -4. 6000 -4. 6464 -4. 6366 -4. 6388 -4. 6383 -4. 6384 0. 2200 0. 2268 0. 2264 0. 2265 0. 3767 0. 3765 NOTE: Convergence criterion met. Estimation Summary Method Iterations R PPC(B) RPC(B) Objective Observations Read Observations Used Observations Missing Gauss-Newton 5 3. 628 E-6 4. 559 E-6 0. 000021 2. 25 E-10 0. 37647 20 20 0

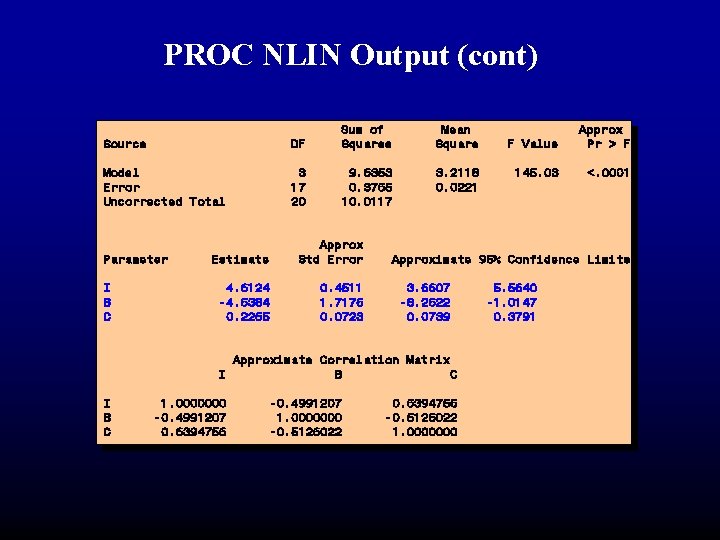
PROC NLIN Output (cont) Source DF Sum of Squares Mean Square Model Error Uncorrected Total 3 17 20 9. 6353 0. 3765 10. 0117 3. 2118 0. 0221 Parameter I B C Estimate Approx Std Error 4. 6124 -4. 6384 0. 2265 0. 4511 1. 7176 0. 0723 1. 0000000 -0. 4991207 0. 6394756 -0. 4991207 1. 0000000 -0. 5126022 Approx Pr > F 145. 03 <. 0001 Approximate 95% Confidence Limits 3. 6607 -8. 2622 0. 0739 Approximate Correlation Matrix I B C F Value 0. 6394756 -0. 5126022 1. 0000000 5. 5640 -1. 0147 0. 3791

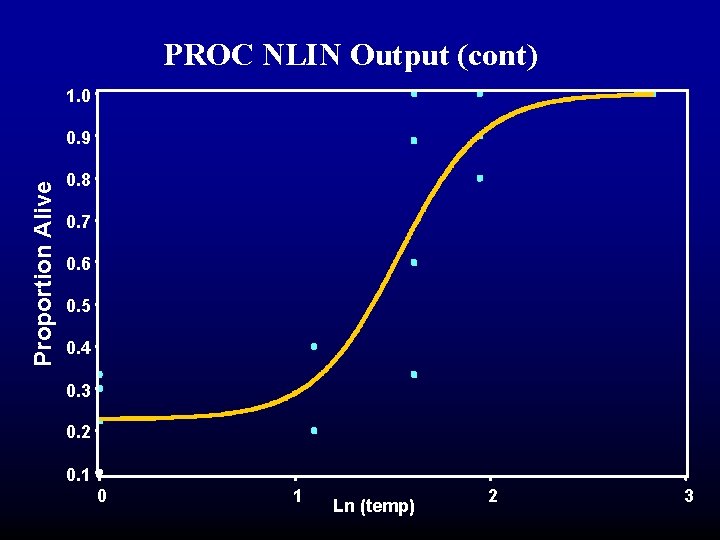
PROC NLIN Output (cont) 1. 0 Proportion Alive 0. 9 0. 8 0. 7 0. 6 0. 5 0. 4 0. 3 0. 2 0. 1 0 1 Ln (temp) 2 3

PROC NLIN (cont) • NLIN Advantages • Not restricted to proportional data. • Maximum may be any value. • Response models not limited. • NLIN Limitations • Assumes normally distributed response. • Approximate tests. • Treatment comparisons not automatic.

Maximum Likelihood • SAS Procedure: PROC NLMIXED • Code: proc nlmixeddata=freezecorr; ; parms I = 4. 5 = -4. 8 =. 228; parms I = B 4. 5 B = C-4. 8 C =. 228; bounds B<0, I>0; bounds mu == CC ++(1 -C)/(1 + exp(B*(ltemp-log(I)))); mu + exp(B*(ltemp-log(I)))); model binomial(plants, mu); model alive 2 wk ~ ~ binomial(plants, mu); model alive 2 wk~ binomial(plants, predict plants*mu out=pred 1; predict muout=pred 2; predict mu mu out=pred 2;

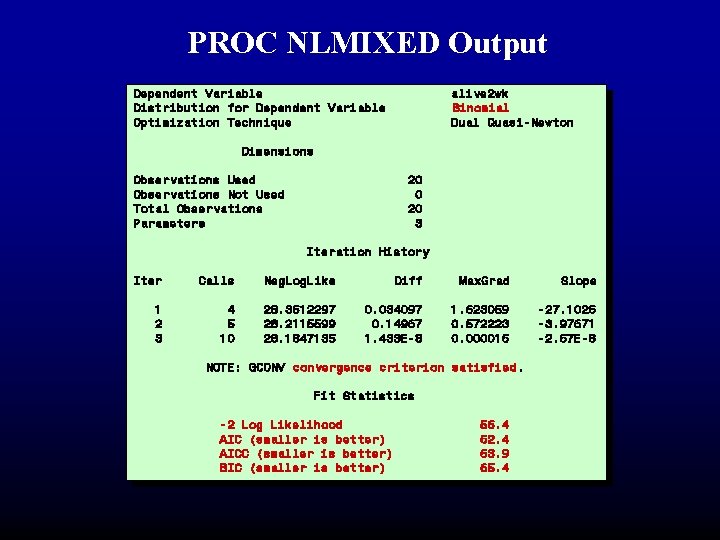
PROC NLMIXED Output Dependent Variable Distribution for Dependent Variable Optimization Technique alive 2 wk Binomial Dual Quasi-Newton Dimensions Observations Used Observations Not Used Total Observations Parameters 20 0 20 3 Iteration History Iter Calls Neg. Log. Like Diff Max. Grad Slope 1 2 3 4 5 10 28. 3612297 28. 2115599 28. 1847135 0. 034097 0. 14967 1. 433 E-8 1. 623059 0. 572223 0. 000016 -27. 1026 -3. 97671 -2. 67 E-8 NOTE: GCONV convergence criterion satisfied. Fit Statistics -2 Log Likelihood AIC (smaller is better) AICC (smaller is better) BIC (smaller is better) 56. 4 62. 4 63. 9 65. 4

PROC NLMIXED Output (cont) Parameter Estimates Parm Estimate I B C 4. 6337 -4. 5094 0. 2258 Standard Error DF t Value Pr > |t| 0. 4151 1. 1543 0. 06231 20 20 20 11. 16 -3. 91 3. 62 <. 0001 0. 0009 0. 0017 Alpha 0. 05 Correlation Matrix of Parameter Estimates Row 1 2 3 Parameter I B C 1. 0000 -0. 5276 0. 5848 -0. 5276 1. 0000 -0. 3896 0. 5848 -0. 3896 1. 0000 Lower 3. 7677 -6. 9172 0. 09585 Upper 5. 4996 -2. 1016 0. 3558 Gradient 4. 629 E-6 -2. 62 E-6 0. 000016

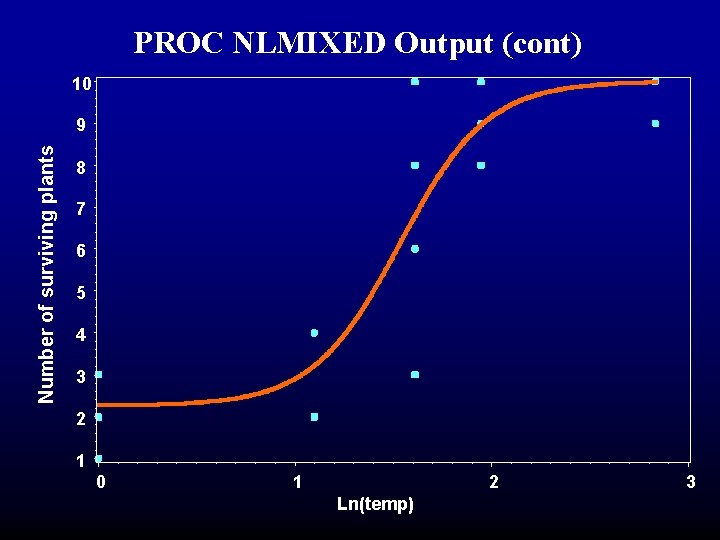
PROC NLMIXED Output (cont) 10 Number of surviving plants 9 8 7 6 5 4 3 2 1 0 1 2 Ln(temp) 3

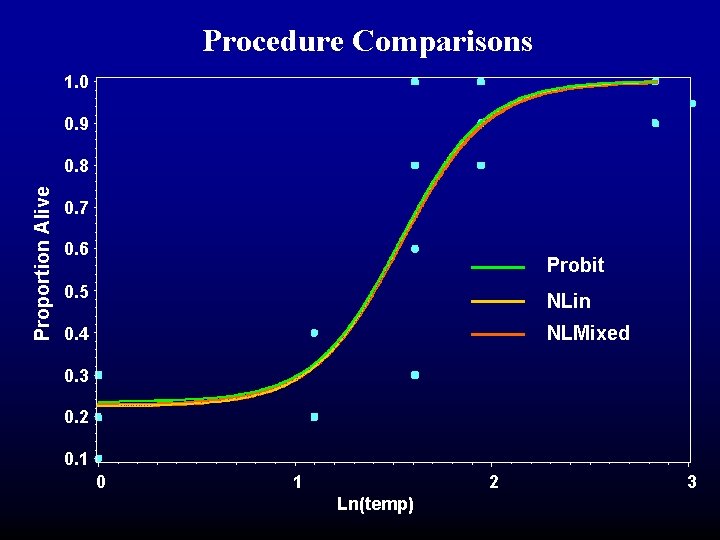
Procedure Comparisons 1. 0 0. 9 Proportion Alive 0. 8 0. 7 0. 6 Probit 0. 5 NLin 0. 4 NLMixed 0. 3 0. 2 0. 1 0 1 2 Ln(temp) 3

Procedure Comparisons • All three procedures can produce similar results. • Binomial or proportional data. • Maximum response of 1. 0. • PROBIT limited in models and response types. • NLIN and NLMIXED provide nonlinear solutions. • NLMIXED most flexible for responses and models.

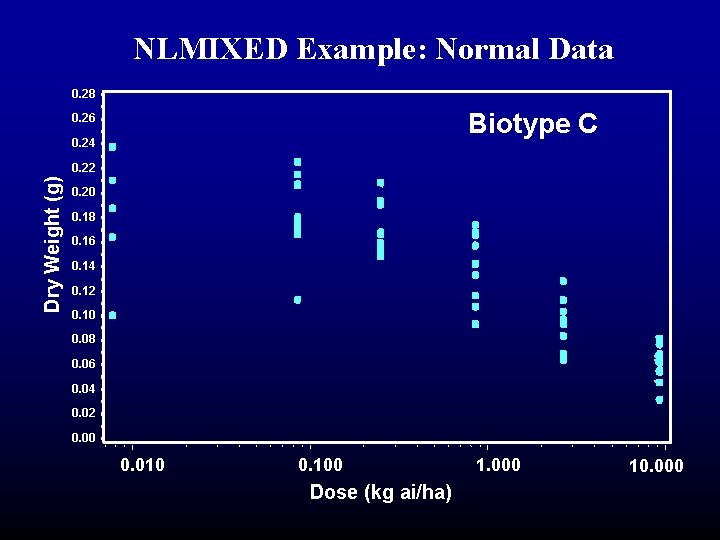
NLMIXED Example: Normal Data • NLMIXED probability distributions: • • Binomial - yes/no data. Normal - continuous data. Poisson - discrete count data. User defined - any data. • Example: Seefeldt, et al. 1995 • Wild oat resistance • Treated with fenoxaprop/2, 4 -D/MCPA (SAS: dose). • Dry weights at 2 weeks (SAS: adj_wt).

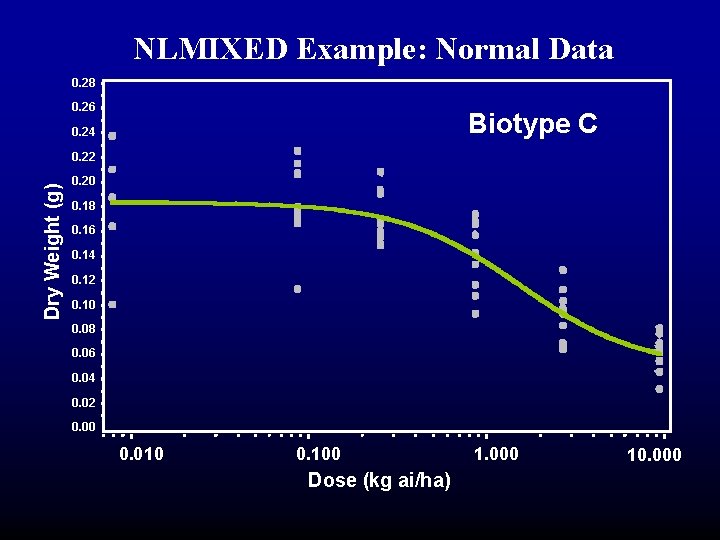
NLMIXED Example: Normal Data 0. 28 Biotype C 0. 26 0. 24 Dry Weight (g) 0. 22 0. 20 0. 18 0. 16 0. 14 0. 12 0. 10 0. 08 0. 06 0. 04 0. 02 0. 00 0. 010 0. 100 Dose (kg ai/ha) 1. 000 10. 000

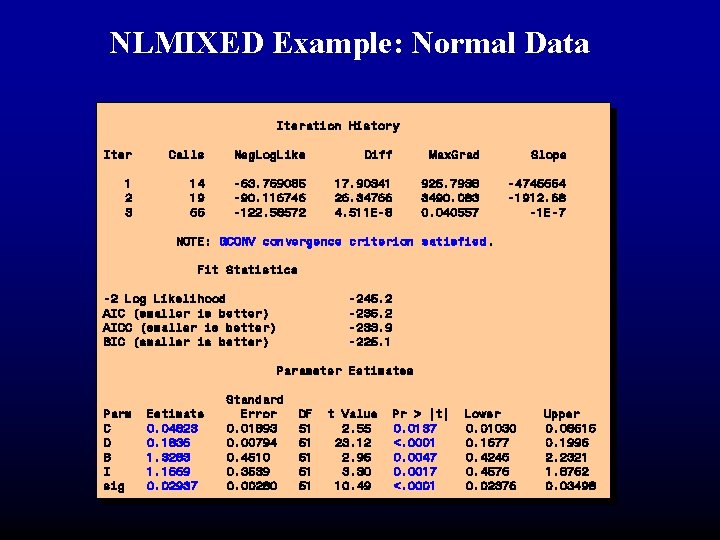
NLMIXED Example: Normal Data • Assume dry weight to be normally distributed with mean mu and variance sig 2. • Must model sig explicitly. proc nlmixed data=seefeldt; parms C=. 04 D=. 2 B=3 I=. 1 sig=. 021; bounds C>0, D>0, B>0, sig>0; if dose = 0 then mu = D; else mu = C + (D-C)/(1 + exp(B*(ldose-log(I)))); model adj_wt ~ normal(mu, sig**2); predict mu out=fitted;

NLMIXED Example: Normal Data Iteration History Iter Calls Neg. Log. Like Diff Max. Grad Slope 1 2 3 14 19 66 -63. 769085 -90. 116746 -122. 58572 17. 90341 26. 34766 4. 511 E-8 925. 7938 3490. 083 0. 040557 -4745664 -1912. 68 -1 E-7 NOTE: GCONV convergence criterion satisfied. Fit Statistics -2 Log Likelihood AIC (smaller is better) AICC (smaller is better) BIC (smaller is better) -245. 2 -233. 9 -225. 1 Parameter Estimates Parm C D B I sig Estimate 0. 04823 0. 1836 1. 3283 1. 1669 0. 02937 Standard Error 0. 01893 0. 00794 0. 4510 0. 3539 0. 00280 DF 51 51 51 t Value 2. 55 23. 12 2. 95 3. 30 10. 49 Pr > |t| 0. 0137 <. 0001 0. 0047 0. 0017 <. 0001 Lower 0. 01030 0. 1677 0. 4246 0. 4576 0. 02376 Upper 0. 08616 0. 1996 2. 2321 1. 8762 0. 03498

NLMIXED Example: Normal Data 0. 28 0. 26 Biotype C 0. 24 Dry Weight (g) 0. 22 0. 20 0. 18 0. 16 0. 14 0. 12 0. 10 0. 08 0. 06 0. 04 0. 02 0. 00 0. 010 0. 100 Dose (kg ai/ha) 1. 000 10. 000

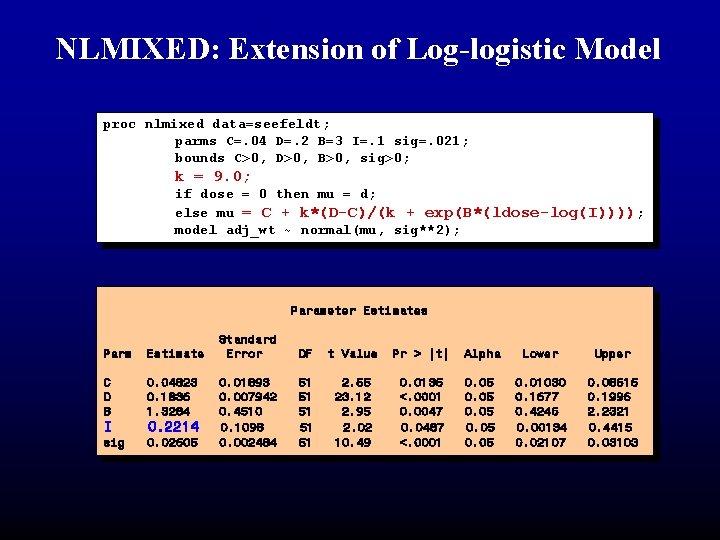
NLMIXED: Extension of Log-logistic Model • The log-logistic model can be generalized to estimate any percentile as (Schabenberger, 1999): yij = C + k (D - C) / (k + exp(B( dosei – I(1 -Q) ))) where I(1 -Q) is the dose required to reach the Qth percentile, and k is given by : k = Q/(1 - Q)

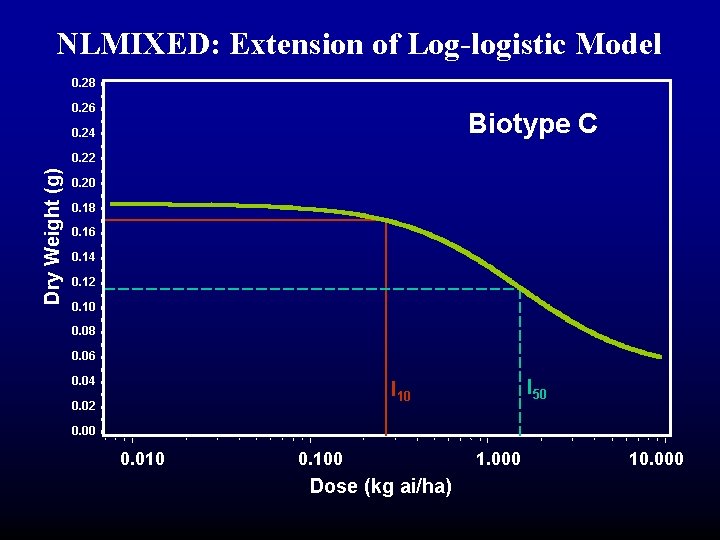
NLMIXED: Extension of Log-logistic Model • Example: • Seefeldt data, biotype C. • Estimate the 90 th percentile, e. g. I 10 Q = 0. 9 k = Q/(1 - Q) = 0. 9/(1. 0 - 0. 9) = 9. 0

NLMIXED: Extension of Log-logistic Model proc nlmixed data=seefeldt; parms C=. 04 D=. 2 B=3 I=. 1 sig=. 021; bounds C>0, D>0, B>0, sig>0; k = 9. 0; if dose = 0 then mu = d; else mu = C + k*(D-C)/(k + exp(B*(ldose-log(I)))); model adj_wt ~ normal(mu, sig**2); Parameter Estimates Parm Estimate C D B 0. 04823 0. 1836 1. 3284 sig 0. 02605 I 0. 2214 Standard Error DF t Value Pr > |t| Alpha Lower Upper 0. 01893 0. 007942 0. 4510 0. 1098 0. 002484 51 51 51 2. 55 23. 12 2. 95 2. 02 10. 49 0. 0136 <. 0001 0. 0047 0. 0487 <. 0001 0. 05 0. 01030 0. 1677 0. 4246 0. 00134 0. 02107 0. 08616 0. 1996 2. 2321 0. 4415 0. 03103

NLMIXED: Extension of Log-logistic Model 0. 28 0. 26 Biotype C 0. 24 Dry Weight (g) 0. 22 0. 20 0. 18 0. 16 0. 14 0. 12 0. 10 0. 08 0. 06 0. 04 I 50 I 10 0. 02 0. 00 0. 010 0. 100 Dose (kg ai/ha) 1. 000 10. 000

NLMIXED Example: Treatment Structure • NLMIXED can accommodate treatment structure: • • SAS Data Step statements. Build full model. Estimates pooled or heterogeneous error. Estimate and Contrast statements for treatment comparisons. • Example: Seefeldt, et al. 1995 • Wild oat resistance to fenoxaprop (SAS: dose). • Dry weights at 2 weeks (SAS: adj_wt). • Three biotypes ; w, b, and c (SAS: biotype).

NLMIXED Example: Treatment Structure • Specify a full model with: • Independent parameters B and I for each biotype. • Common parameter values for C, D, and sig. Wt = C + (D - C) / (1 + exp(B(dosei - I))) where B and I are dependent on biotype.

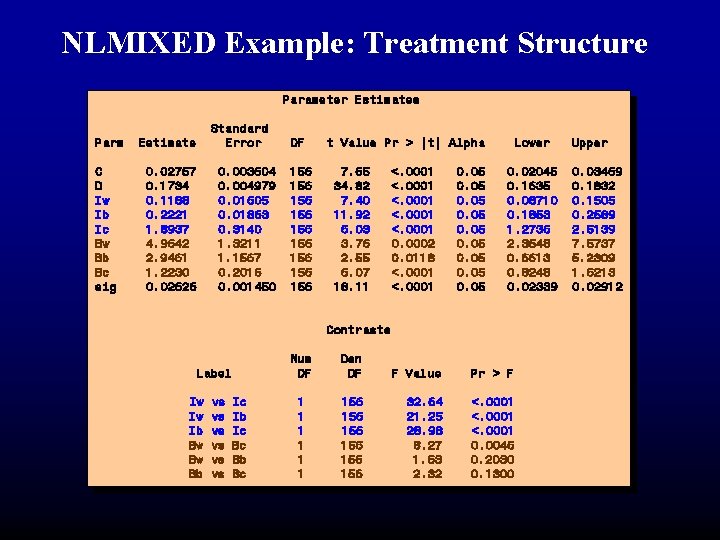
NLMIXED Example: Treatment Structure proc nlmixed data=seefeldt; parms D=. 1734 Iw=. 1188 Ib=. 2221 Ic=1. 8936 parms C=. 02757 D=. 1734 Iw=. 1188 Ib=. 2221 Ic=1. 8936 Bw=4. 9642 Bb=2. 9461 Bc=1. 223 sig=. 021; bounds C>0, D>0, Bc>0, Bw>0, Bb>0, sig>0; if then do; if biotype= ’w' then if biotype = =’w' then do; I = Iw; B=Bw; I == Iw; B=Bw; end; else if biotype = then do; else = 'c' then do; else if ifbiotype = 'c' then I = Ic; B=Bc; I I == Ic; B=Bc; end; else if if biotype = = 'b' then do; else if I biotype = 'b' then do; = Ib; B=Bb; I = Ib; B=Bb; end; if if dose = = 0 0 then mu mu = = D; D; else mu = C + (D-C)/(1 + else mu = 0 C then + (D-C)/(1 + exp(B*(ldose-log(I)))); if dose mu = D; model adj_wt ~ normal(mu, sig**2); model adj_wt normal(mu, sig**2); else mu = C +~(D-C)/(1 + exp(B*(ldose-log(I)))); model adj_wt ~ normal(mu, sig**2); contrast 'Iwvsvs Iw-Ic; contrast 'Iw Ic'Ic' Iw-Ic; contrast 'Iwvsvs Iw-Ib; contrast 'Iw Ib' Iw-Ib; Ic'Ib' Iw-Ic; contrast 'Ib Ic' Ib-Ic; 'Iw Ib'Ic' Iw-Ib; contrast 'Ibvsvs Ib-Ic; predict out=fitted; contrastmu 'Ib vs Ic' Ib-Ic; predict mu out=fitted;

NLMIXED Example: Treatment Structure Parameter Estimates Parm C D Iw Ib Ic Bw Bb Bc sig Estimate 0. 02757 0. 1734 0. 1188 0. 2221 1. 8937 4. 9642 2. 9461 1. 2230 0. 02626 Standard Error 0. 003604 0. 004979 0. 01605 0. 01863 0. 3140 1. 3211 1. 1567 0. 2016 0. 001450 DF 156 156 156 t Value Pr > |t| Alpha 7. 65 34. 82 7. 40 11. 92 6. 03 3. 76 2. 55 6. 07 18. 11 <. 0001 0. 0002 0. 0118 <. 0001 0. 05 0. 05 Lower 0. 02045 0. 1635 0. 08710 0. 1853 1. 2736 2. 3548 0. 6613 0. 8248 0. 02339 Contrasts Label Iw Iw Ib Bw Bw Bb vs vs vs Ic Ib Ic Bc Bb Bc Num DF Den DF F Value Pr > F 1 1 1 156 156 156 32. 64 21. 25 28. 98 8. 27 1. 63 2. 32 <. 0001 0. 0046 0. 2030 0. 1300 Upper 0. 03469 0. 1832 0. 1505 0. 2589 2. 5139 7. 5737 5. 2309 1. 6213 0. 02912

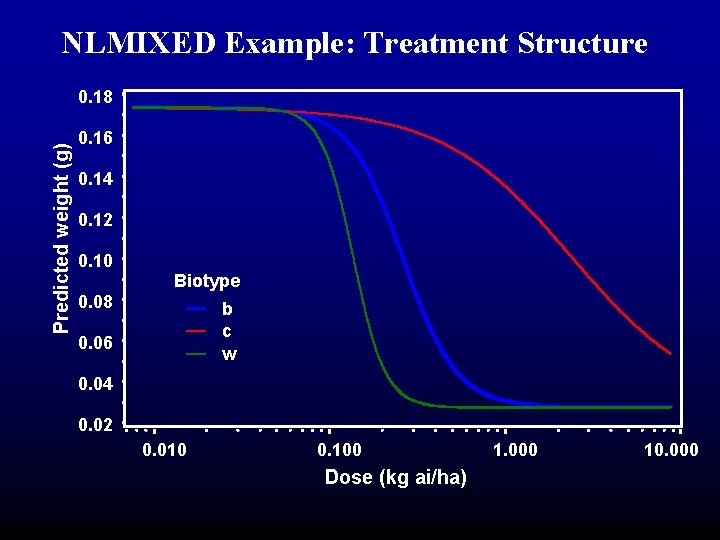
NLMIXED Example: Treatment Structure Predicted weight (g) 0. 18 0. 16 0. 14 0. 12 0. 10 Biotype 0. 08 b c w 0. 06 0. 04 0. 02 0. 010 0. 100 Dose (kg ai/ha) 1. 000 10. 000

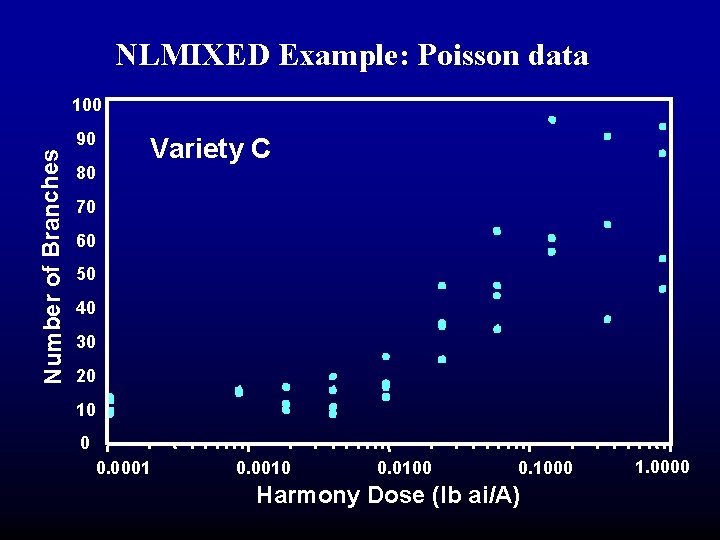
NLMIXED Example: Poisson data • Data description • Simulated injury study. • Harmony sprayed on pea plants. • measured the number of branches/plant. • (SAS: branches). • Ten doses: • 0 to 0. 125 lbs ai/A. • (SAS: trt).

NLMIXED Example: Poisson data Number of Branches 100 90 80 Variety C 70 60 50 40 30 20 10 0 0. 0001 0. 0010 0. 0100 0. 1000 Harmony Dose (lb ai/A) 1. 0000

NLMIXED Example: Poisson data • Assume the number of branches to be distributed as a Poisson variable. • In the Poisson distribution, mean = variance = mu. proc nlmixed data=pea; parms D=10 C=70 B=. 8254 I=. 01; bounds D>0, B>0; if trt = 0 then mu = D; else mu = C + (D-C)/(1 + exp(B*(ltrt-log(I)))); model branches ~ poisson(mu); predict mu out=pred;

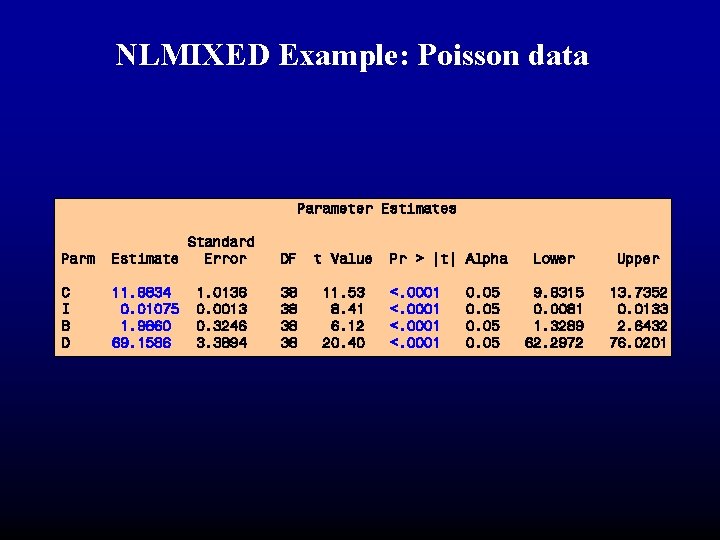
NLMIXED Example: Poisson data Parameter Estimates Parm Standard Estimate Error DF t Value C I B D 11. 6834 0. 01075 1. 9860 69. 1586 38 38 11. 53 8. 41 6. 12 20. 40 1. 0136 0. 0013 0. 3246 3. 3894 Pr > |t| Alpha <. 0001 0. 05 Lower Upper 9. 6315 0. 0081 1. 3289 62. 2972 13. 7352 0. 0133 2. 6432 76. 0201

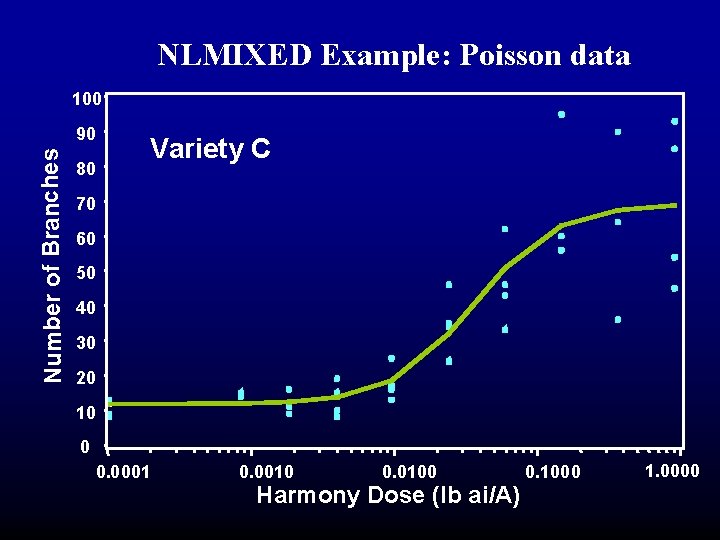
NLMIXED Example: Poisson data 100 Number of Branches 90 80 Variety C 70 60 50 40 30 20 10 0 0. 0001 0. 0010 0. 0100 Harmony Dose (lb ai/A) 0. 1000 1. 0000

NLMIXED: Alternative Models Example: • Log-logistic Model yij = C + (D - C) / (1 + exp(B(dosei - I))) • Exponential Model yij = (a-c) exp(-b dose) + c

Exponential Model for Pea Biomass • A linear pattern of data on a log scale. • Implies an exponential model, e. g. Biomass = (a-c) exp(-b dose) + c where a is an intercept term, c is a lower limit and b is a rate parameter. • The 50 th percentile for this model is given by: I 50 = ln(((a/2) - c)/(a - c))/(-b)

NLMIXED: Alternative Models • Example: Pea Data • Fit log-logistic model to biomass measurements. proc nlmixed data=pea corr maxiter=2000; parms D=. 5966 I=0. 01 B=. 51 C=. 04 sig=. 09; bounds D>0, B>0; if trt = 0 then mu = D; else mu = C + (D-C)/(1 + exp(B*(ltrt-log(I)))); model bio ~ normal(mu, sig**2);

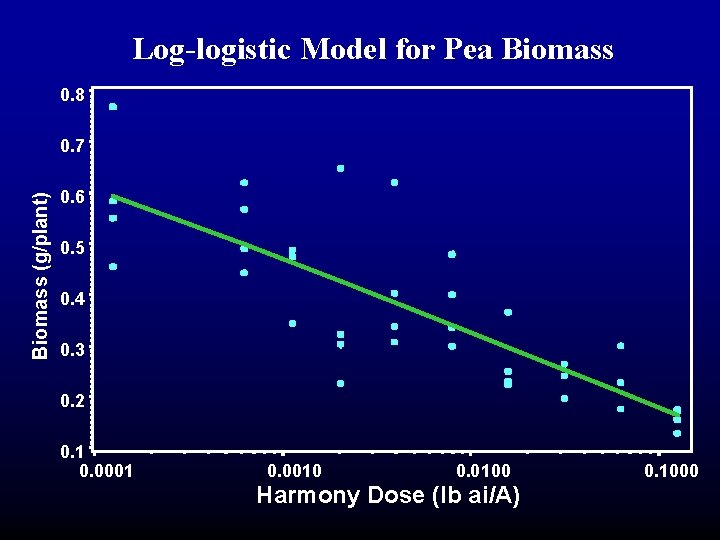
Log-logistic Model for Pea Biomass 0. 8 Biomass (g/plant) 0. 7 0. 6 0. 5 0. 4 0. 3 0. 2 0. 1 0. 0001 0. 0010 0. 0100 Harmony Dose (lb ai/A) 0. 1000

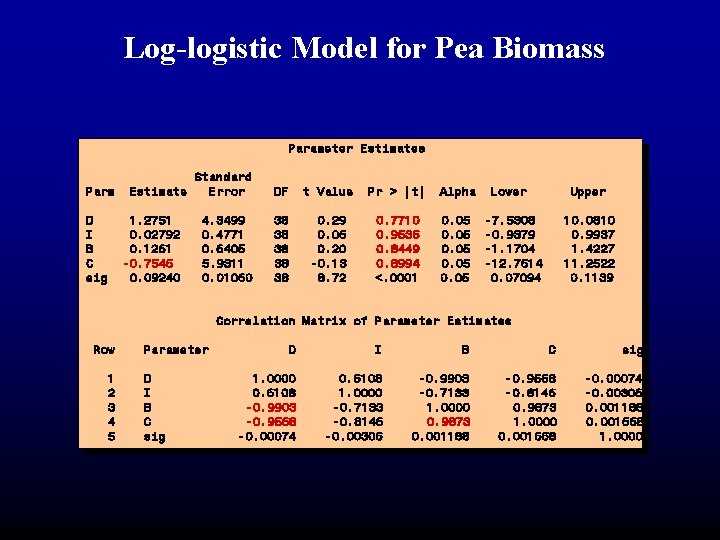
Log-logistic Model for Pea Biomass Parameter Estimates Parm D I B C sig Estimate 1. 2751 0. 02792 0. 1261 -0. 7546 0. 09240 Standard Error DF t Value Pr > |t| Alpha 4. 3499 0. 4771 0. 6405 5. 9311 0. 01060 38 38 38 0. 29 0. 06 0. 20 -0. 13 8. 72 0. 7710 0. 9536 0. 8449 0. 8994 <. 0001 0. 05 Lower Upper -7. 5308 -0. 9379 -1. 1704 -12. 7614 0. 07094 10. 0810 0. 9937 1. 4227 11. 2522 0. 1139 Correlation Matrix of Parameter Estimates Row 1 2 3 4 5 Parameter D I B C sig 1. 0000 0. 6108 -0. 9903 -0. 9568 -0. 00074 0. 6108 1. 0000 -0. 7133 -0. 8146 -0. 00306 -0. 9903 -0. 7133 1. 0000 0. 9873 0. 001188 -0. 9568 -0. 8146 0. 9873 1. 0000 0. 001668 -0. 00074 -0. 00306 0. 001188 0. 001668 1. 0000

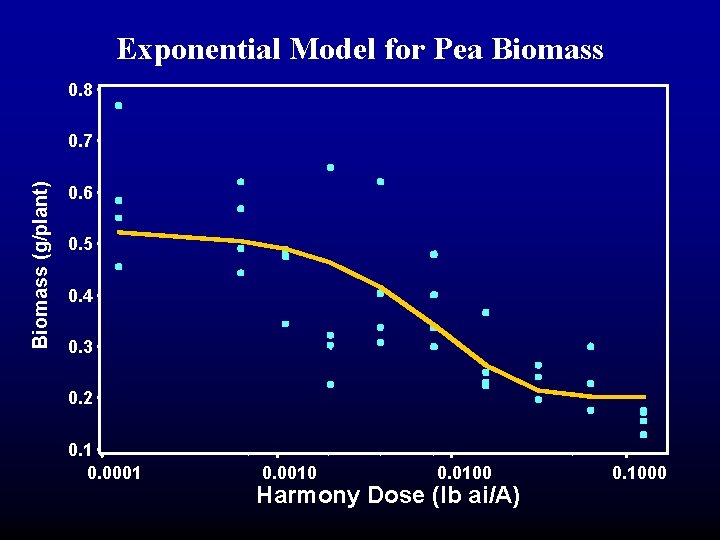
Exponential Model for Pea Biomass proc nlmixed data=pea corr; parms a=. 5217 b=106. 5 c =. 2026 sig=. 09; mu =(a-c)*exp(-b*trt) + c; model bio ~ normal(mu, sig**2); predict mu out=pred; estimate ’I 50' log(((a/2)-c)/(a-c))/(-b);

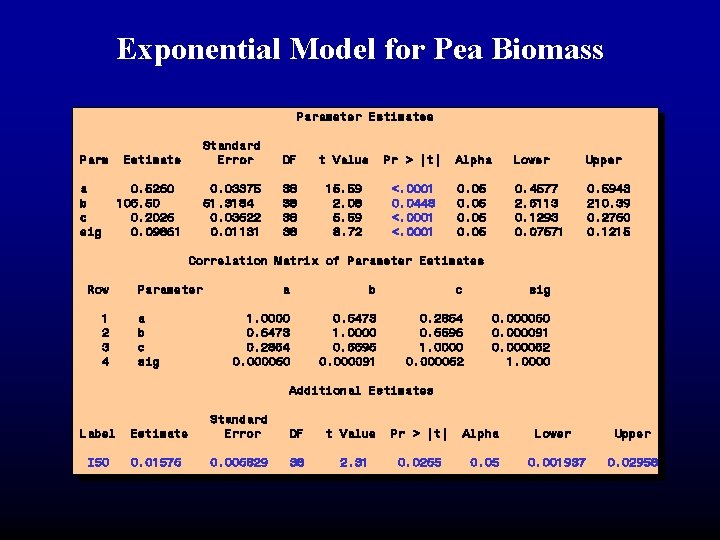
Exponential Model for Pea Biomass Parameter Estimates Estimate Standard Error DF t Value Pr > |t| Alpha Lower Upper 0. 5260 106. 50 0. 2026 0. 09861 0. 03375 51. 3184 0. 03622 0. 01131 38 38 15. 59 2. 08 5. 59 8. 72 <. 0001 0. 0448 <. 0001 0. 05 0. 4577 2. 6113 0. 1293 0. 07571 0. 5943 210. 39 0. 2760 0. 1215 Parm a b c sig Correlation Matrix of Parameter Estimates Row 1 2 3 4 Parameter a b c sig 1. 0000 0. 6473 0. 2864 0. 000060 0. 6473 1. 0000 0. 6696 0. 000091 0. 2864 0. 6696 1. 0000 0. 000062 0. 000060 0. 000091 0. 000062 1. 0000 Additional Estimates Label I 50 Estimate Standard Error DF 0. 01576 0. 006829 38 t Value 2. 31 Pr > |t| 0. 0265 Alpha 0. 05 Lower 0. 001937 Upper 0. 02958

Exponential Model for Pea Biomass 0. 8 Biomass (g/plant) 0. 7 0. 6 0. 5 0. 4 0. 3 0. 2 0. 1 0. 0001 0. 0010 0. 0100 Harmony Dose (lb ai/A) 0. 1000

Nonlinear Mixed Models • Random effects may also be modeled. • Locations. • Years. • Experiments/replications. • See for example Nielson, et al 2004. • Components estimated. • Within effects - Variances. • Between effects - Covariances. • Requires caution. • Parsimony. • Estimation problems.

Nonlinear Mixed Models • Example: Fungus Gnat Data. • Evaluate efficacy of rapeseed meal (SAS: dose). • Three experiments. • Separate runs for each block (SAS: block). • Measured egg hatch (SAS: mort). • High variability in natural mortality from run to run.

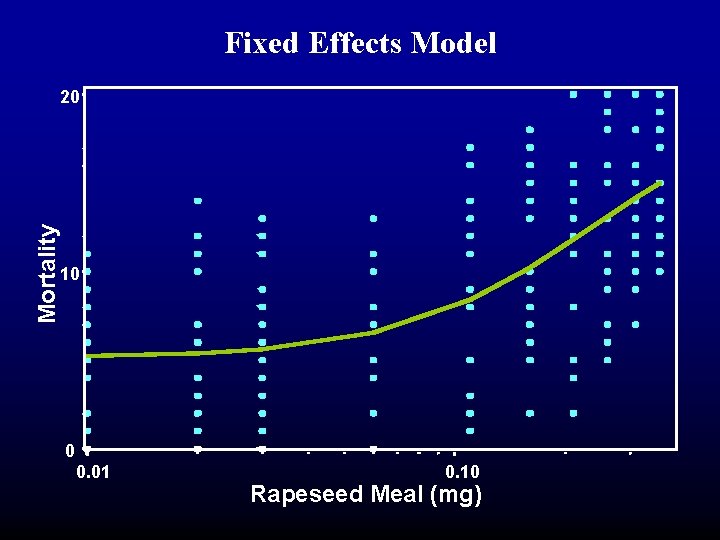
Nonlinear Mixed Models • Fixed effects model: proc nlmixed maxiter=1000 data=gnat 2; parms I=. 245 B=-3. 58 c=. 295; bounds B<0, C>0, I>0; if dose = 0 then mu = c; else mu = c + (1 -c)/(1 + exp(B*(ldose-log(I)))); model mort ~ binomial(20, mu); predict mu*20 out=pred 1; run;

Nonlinear Mixed Models • Fixed effects model: Fit Statistics -2 Log Likelihood AIC (smaller is better) AICC (smaller is better) BIC (smaller is better) 1593. 6 1599. 8 1609. 5 Parameter Estimates Parm Estimate I B c 0. 2387 -1. 6369 0. 2567 Standard Error 0. 01117 0. 1708 0. 01610 DF t Value Pr > |t| 200 200 21. 38 -9. 59 15. 94 <. 0001 Alpha 0. 05 Lower Upper 0. 2167 -1. 9736 0. 2249 0. 2607 -1. 3002 0. 2884

Fixed Effects Model Mortality 20 10 0 0. 01 0. 10 Rapeseed Meal (mg)

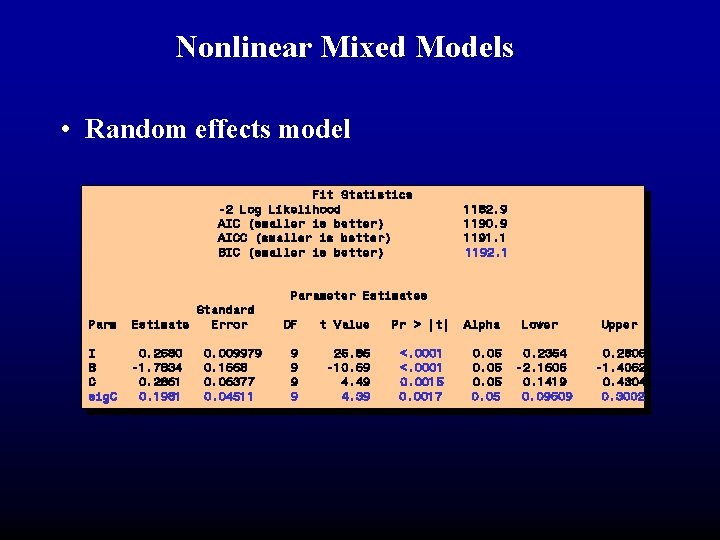
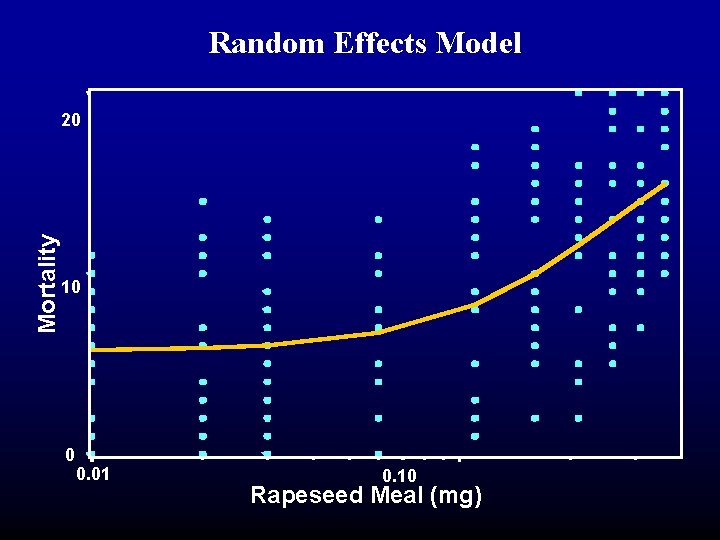
Nonlinear Mixed Models • Random effects model: • Let natural mortality parameter, C, be random. proc nlmixed maxiter=1000 data=gnat 2; parms I=. 2582 B=-1. 78 C=. 2866 sig. C=. 17; bounds B<0, c>0, I>0; Ce = C + e; if dose = 0 then mu = Ce; else mu = Ce + (1 -Ce)/(1 + exp(B*(ldose-log(I)))); model mort ~ binomial(20, mu); random e~normal(0, sig. C**2) subject=block;

Nonlinear Mixed Models • Random effects model Fit Statistics -2 Log Likelihood AIC (smaller is better) AICC (smaller is better) BIC (smaller is better) Parm Standard Estimate Error I B C sig. C 0. 2580 -1. 7834 0. 2861 0. 1981 0. 009979 0. 1668 0. 06377 0. 04511 1182. 9 1190. 9 1191. 1 1192. 1 Parameter Estimates DF t Value Pr > |t| 9 9 25. 85 -10. 69 4. 49 4. 39 <. 0001 0. 0015 0. 0017 Alpha 0. 05 Lower 0. 2354 -2. 1606 0. 1419 0. 09609 Upper 0. 2805 -1. 4062 0. 4304 0. 3002

Random Effects Model Mortality 20 10 0 0. 01 0. 10 Rapeseed Meal (mg)

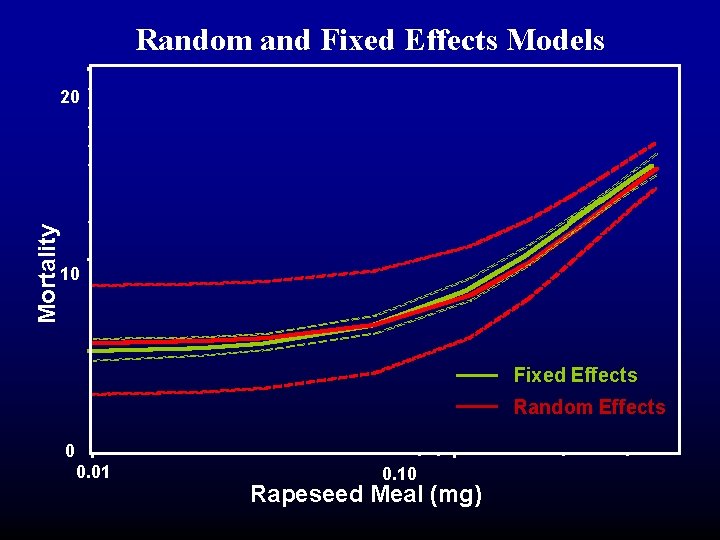
Random and Fixed Effects Models Mortality 20 10 Fixed Effects Random Effects 0 0. 01 0. 10 Rapeseed Meal (mg)

Nonlinear Mixed Models • In general, random effects models: • Are useful with identifiable sources of variability. • Increase overall variability. • Improve measures of fit. • However: • They may not be parsimonious. • They can be difficult to fit.

References • Nielson, O. K. , C. Ritz, J. C. Streibig. 2004. Nonlinear mixed-model regression to analyze herbicide dose-response relationships. Weed Technonlogy, 18: 30 -37. • Ratkowsky, D. A. 1989. Handbook of Nonlinear Regression Models. Marcel Dekker, Inc. 241 pp. • SAS Inst. Inc. 2004. SAS Online. Doc, Version 9, Cary, NC. • Schabenberger, O. , B. E. Tharp, J. J. Kells, and D. Penner. 1999. Statistical tests for hormesis and effective dosages in herbicide dose response. Agron. J. 91: 713 -721. • Seefeldt, S. S. , J. E. Jensen, and P. Fuerst. 1995. Log-logistic analysis of herbicide dose-response relationships. Weed Technol. 9: 218 -227.

Questions / Comments http: //www. uidaho. edu/ag/statprog