PPTCANMTALA 07001 V 1 MT 21 Clase Nmeros






















- Slides: 28

PPTCANMTALA 07001 V 1 MT 21 Clase Números

Aprendizajes esperados • Identificar pertenencia de números a los conjuntos numéricos. • Reconocer los números a través de sus características. • Comparar distintos tipos de números. • Aplicar conceptos aritméticos (números primos, pares, impares, múltiplos y divisores). • Transformar decimales a fracciones y viceversa. • Aplicar características numéricas en la resolución de problemas.

Pregunta oficial PSU 14. La suma de tres números impares consecutivos es siempre I) divisible por 3. II) divisible por 6. III) divisible por 9. Es (son) verdadera(s) A) B) C) D) E) solo I y III. solo II y III. I, II y III. Fuente : DEMRE - U. DE CHILE, Proceso de admisión 2010.

1. Conjuntos numéricos 2. Definiciones 3. Orden 4. Transformaciones 5. M. C. D. y m. c. m. 6. Propiedades

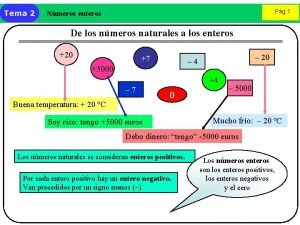
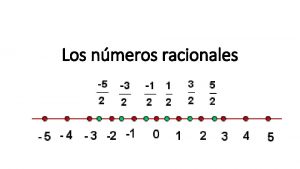
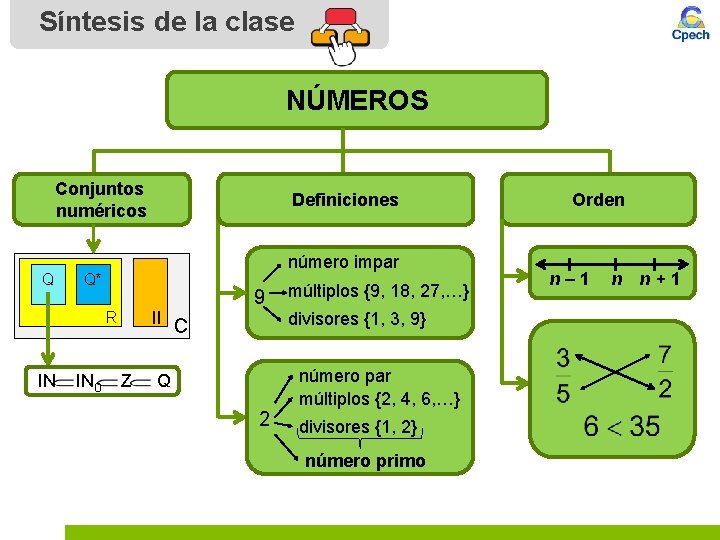
1. Conjuntos numéricos • Naturales: IN = {1, 2, 3, 4, 5, …} • Cardinales: IN 0 = {0, 1, 2, 3, 4, 5, …} • Enteros: Z = {…, – 3, – 2, – 1, 0, 1, 2, 3, …} • Racionales: Q= a / a y b son enteros, y b es distinto de cero b Todo número entero es racional IN • Irracionales: IN 0 Z a: numerador y b: denominador Q Q* = Son aquellos números que NO se pueden escribir como una fracción

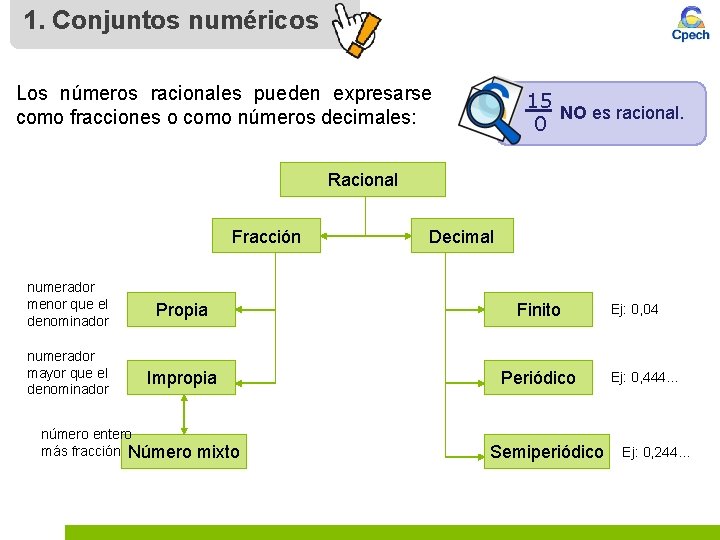
1. Conjuntos numéricos Los números racionales pueden expresarse como fracciones o como números decimales: 15 NO es racional. 0 Racional Fracción Decimal numerador menor que el denominador Propia Finito numerador mayor que el denominador Impropia Periódico número entero más fracción Número mixto Semiperiódico Ej: 0, 04 Ej: 0, 444… Ej: 0, 244…

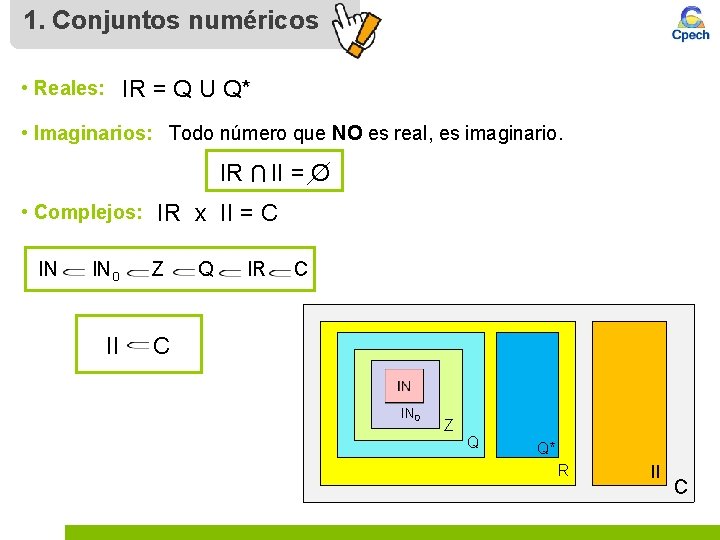
1. Conjuntos numéricos • Reales: IR = Q U Q* • Imaginarios: Todo número que NO es real, es imaginario. U IR II = O • Complejos: IR x II = C IN IN 0 Z II C Q IR C IN 0 Z Q Q* R II C

2. Definiciones 2. 1 Paridad e imparidad • Números pares Son de la forma 2 n, con n en los naturales. {2, 4, 6, 8, 10, …, 2 n} • Números impares Son de la forma 2 n – 1, con n en los naturales. {1, 3, 5, 7, 9, …, 2 n – 1} 2. 2 Múltiplos Los múltiplos de un número son aquellos números que se obtienen al multiplicar dicho número por algún número natural. Por ejemplo, 5, 10, 30, 45 son múltiplos de 5.

2. Definiciones 2. 3 Divisores Los divisores de un número son aquellos números naturales que lo dividen exactamente (división con resto cero). Por ejemplo, los divisores de 24 son 1, 2, 3, 4, 6, 8, 12 y 24. 2. 4 Números primos Son aquellos números naturales que solo son divisibles por 1 y por sí mismos (solo tienen 2 divisores). {2, 3, 5, 7, 11, 13, 17, 19, 23, 29, …}. El 1 NO es primo, pues tiene un solo divisor.

3. Orden 3. 1 Consecutividad numérica • Sucesor Todo número natural tiene un sucesor, y se obtiene sumando 1 al número, es decir: Si n pertenece a IN, su sucesor será n + 1. • Antecesor Todo número natural (exceptuando el 1) tiene un antecesor y se obtiene al restar 1 al número, es decir: Si n pertenece a IN – {1}, su antecesor será n – 1. Naturales consecutivos n– 1 antecesor n n+1 sucesor

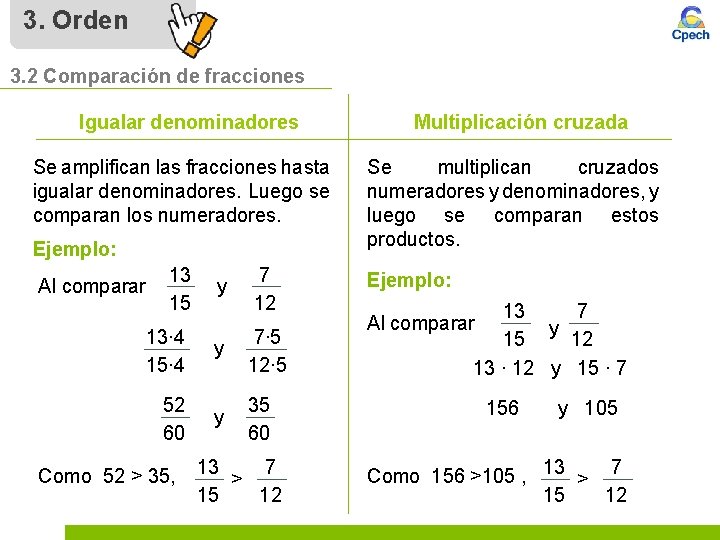
3. Orden 3. 2 Comparación de fracciones Igualar denominadores Se amplifican las fracciones hasta igualar denominadores. Luego se comparan los numeradores. Ejemplo: 13 15 y 13∙ 4 15∙ 4 y 7∙ 5 12∙ 5 52 60 y 35 60 Al comparar Como 52 > 35, 7 12 13 7 > 15 12 Multiplicación cruzada Se multiplican cruzados numeradores y denominadores, y luego se comparan estos productos. Ejemplo: 7 13 y 12 15 13 ∙ 12 y 15 ∙ 7 Al comparar 156 y 105 Como 156 >105 , 13 > 7 12 15

4. Transformaciones • De número mixto a fracción impropia Se debe multiplicar el número entero por el denominador, luego a este producto se le suma el numerador. Este resultado pasa a ser el nuevo numerador y el denominador se mantiene. Ejemplo: • De fracción a decimal Se debe dividir el numerador por el denominador. Ejemplo:

4. Transformaciones • De decimal finito a fracción El numerador, de la nueva fracción, corresponde al decimal pero sin coma. El denominador es una potencia de 10 con tantos ceros como decimales tuviera el racional a transformar. Ejemplo: • De decimal periódico a fracción 1. El numerador de la fracción es la diferencia entre el número decimal completo, sin la coma, y la parte entera. 2. El denominador está formado por tantos nueves (9), como cifras tenga el período. Ejemplos: Se llama período al conjunto de dígitos que se repite indefinidamente.

4. Transformaciones • De decimal semiperiódico a fracción 1. El numerador de la fracción corresponde a la diferencia entre el número decimal completo, sin la coma; y la parte entera incluyendo las cifras del anteperiodo. 2. El denominador queda formado por tantos nueves (9), como cifras tenga el período, y tantos ceros (0), como cifras tenga el anteperiodo. Ejemplo: 3, 214 = 3. 214 -32 = 3. 182 990 Se llama anteperiodo a los números que hay entre la coma decimal y el período.

5. M. C. D y m. c. m. • Mínimo común múltiplo (m. c. m. ) El mínimo común múltiplo (m. c. m. ) de dos o más números, corresponde al menor de los múltiplos que tienen en común. El m. c. m. entre 3, 6 y 15 se puede obtener a través del siguiente método: Se divide cada número por números primos hasta que en cada columna quede 1. El producto de ellos corresponde al m. c. m. entre 3, 6 y 15. 3 6 15 3 1 2 5 2 1 5 5 1 m. c. m. = 3 ∙ 2 ∙ 5 = 30

5. M. C. D y m. c. m. • Máximo común divisor (M. C. D. ) El máximo común divisor de dos o más números, corresponde al mayor número que los divide simultáneamente. El M. C. D. entre 36, 18 y 24 se puede obtener a través del siguiente método: Se divide por números primos que sean divisores de cada número, hasta que ya no se pueda dividir a todos en forma simultánea. La multiplicación de estos primos es el M. C. D. 36 18 24 2 18 9 12 3 6 3 4 M. C. D. = 2 ∙ 3 = 6

6. Propiedades Valor absoluto o módulo El valor absoluto de un número representa la distancia del número al cero en la recta numérica. Por ejemplo, la distancia del 5 al origen es cinco unidades, igual que la distancia del (– 5) al origen. La notación es: |5| = 5 y |– 5| = 5 0 -5 Ejemplo: 5 unidades |– 20| = 20 5 5 unidades |34| = 34 |– 12| = 12

6. Propiedades 6. 1 Propiedades en N Propiedades de la adición a) Clausura: la suma de dos números naturales es SIEMPRE un natural. b) Conmutatividad: si a y b son números naturales, entonces se cumple que: a+b=b+a c) Asociatividad: si a, b y c son números naturales, entonces se cumple que: a + (b + c) = (a + b) + c En los naturales NO existe neutro aditivo.

6. Propiedades 6. 1 Propiedades en N Propiedades de la multiplicación a ∙ b = c, donde a y b factores y c producto. a) Clausura: el producto de dos números naturales es SIEMPRE un natural. b) Conmutatividad: si a y b son números naturales, entonces se cumple que: a∙b=b∙a c) Asociatividad: si a, b y c son números naturales, entonces se cumple que: a ∙ (b ∙ c) = (a ∙ b) ∙ c d) Elemento neutro: el elemento neutro de la multiplicación es el 1, ya que: a∙ 1=1∙a=a

6. Propiedades 6. 2 Propiedades en N 0 En este conjunto, para la adición y la multiplicación, se cumplen las mismas propiedades que en N, solo se agrega la siguiente para la adición: a) Elemento neutro aditivo: el cero es neutro para la adición, ya que a+0=0+a=a y a continuación para la multiplicación: b) Elemento absorbente: el cero absorbe la multiplicación, ya que a∙ 0=0∙a=0

6. Propiedades 6. 3 Propiedades en Z En este conjunto, para la adición y la multiplicación, se cumplen las mismas propiedades que en N 0, solo se agrega la siguiente para la suma: Elemento inverso aditivo (opuesto) : todo número entero posee un elemento inverso aditivo, que cumpla a+–a=0=–a+a Ejemplos: El inverso aditivo de 8 es – 8 El inverso aditivo de – 12 es 12

6. Propiedades 6. 4 Propiedades en Q Para la multiplicación se cumplen las mismas propiedades que en Z, solo se agrega la siguiente: Elemento inverso multiplicativo o recíproco: todo número racional posee un elemento recíproco, que cumpla a∙ 1 =1= 1 ∙a a a Ejemplo: El inverso multiplicativo o recíproco de 2 9 es 9 2

Pregunta oficial PSU 14. La suma de tres números impares consecutivos es siempre I) divisible por 3. II) divisible por 6. III) divisible por 9. Es (son) verdadera(s) A) B) C) D) E) solo I y III. solo II y III. I, II y III. ALTERNATIVA CORRECTA A Fuente : DEMRE - U. DE CHILE, Proceso de admisión 2010.

Tabla de corrección Ítem Alternativa Unidad temática Habilidad 1 D Conjuntos numéricos Análisis 2 C Conjuntos numéricos Análisis 3 B Conjuntos numéricos Análisis 4 C Conjuntos numéricos Análisis 5 E Conjuntos numéricos Análisis 6 E Conjuntos numéricos Análisis 7 A Conjuntos numéricos Comprensión 8 E Conjuntos numéricos Aplicación 9 B Conjuntos numéricos Aplicación 10 C Conjuntos numéricos Aplicación 11 D Conjuntos numéricos Aplicación 12 D Conjuntos numéricos Aplicación

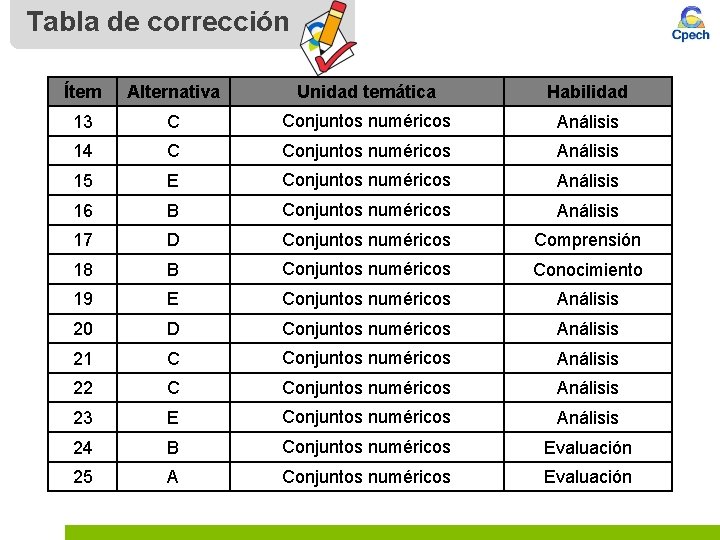
Tabla de corrección Ítem Alternativa Unidad temática Habilidad 13 C Conjuntos numéricos Análisis 14 C Conjuntos numéricos Análisis 15 E Conjuntos numéricos Análisis 16 B Conjuntos numéricos Análisis 17 D Conjuntos numéricos Comprensión 18 B Conjuntos numéricos Conocimiento 19 E Conjuntos numéricos Análisis 20 D Conjuntos numéricos Análisis 21 C Conjuntos numéricos Análisis 22 C Conjuntos numéricos Análisis 23 E Conjuntos numéricos Análisis 24 B Conjuntos numéricos Evaluación 25 A Conjuntos numéricos Evaluación

Síntesis de la clase NÚMEROS Conjuntos numéricos Q número impar Q* II C R IN Definiciones IN 0 Z 9 múltiplos {9, 18, 27, …} divisores {1, 3, 9} Q 2 número par múltiplos {2, 4, 6, …} divisores {1, 2} número primo Orden n– 1 n n+1

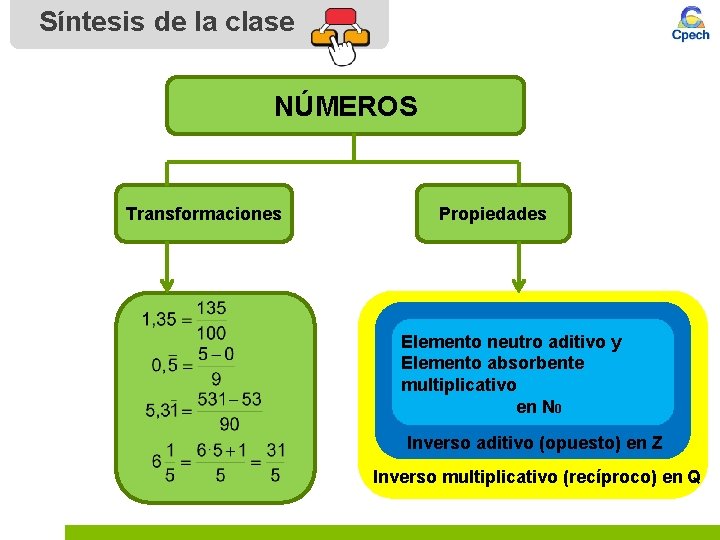
Síntesis de la clase NÚMEROS Transformaciones Propiedades Elemento neutro aditivo y Elemento absorbente multiplicativo en N 0 Inverso aditivo (opuesto) en Z Inverso multiplicativo (recíproco) en Q

Prepara tu próxima clase En la próxima sesión, estudiaremos Operatoria
 Quadrada de 7
Quadrada de 7 Nmeros naturales
Nmeros naturales Numeros romanos del 1 al 100
Numeros romanos del 1 al 100 Temporalidad de los romanos
Temporalidad de los romanos Nmeros enteros
Nmeros enteros Nmeros enteros
Nmeros enteros Nmeros ordinales
Nmeros ordinales Nmeros primos
Nmeros primos Nmeros ordinales
Nmeros ordinales Nmeros reales
Nmeros reales Numeros romanos
Numeros romanos Numerais cardinais
Numerais cardinais Nmeros ordinales
Nmeros ordinales Nmeros reales
Nmeros reales Nmeros naturales
Nmeros naturales Nmeros ordinales
Nmeros ordinales Nmeros enteros
Nmeros enteros Nmeros naturales
Nmeros naturales Primero segundo tercero
Primero segundo tercero Numeros poligonales
Numeros poligonales Nmeros enteros
Nmeros enteros Ivx número romano
Ivx número romano Monomio opuesto
Monomio opuesto Rubrica de observación de clase
Rubrica de observación de clase Isoordinadas ejemplos
Isoordinadas ejemplos Platforma edmodo
Platforma edmodo Sa se imparta nr 301
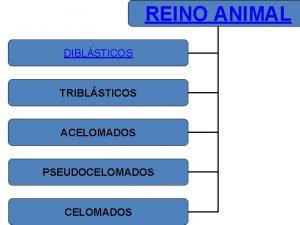
Sa se imparta nr 301 Protostomados
Protostomados Correlaciones espurias ejemplos
Correlaciones espurias ejemplos