Powerful Parametrics for Airfoil Geometry J Philip Barnes

Powerful Parametrics for Airfoil Geometry J. Philip Barnes U 30 Mar, 2015 W W J. Philip Barnes www. How. Flies. The. Albatross. com Pelican Aero Group 1

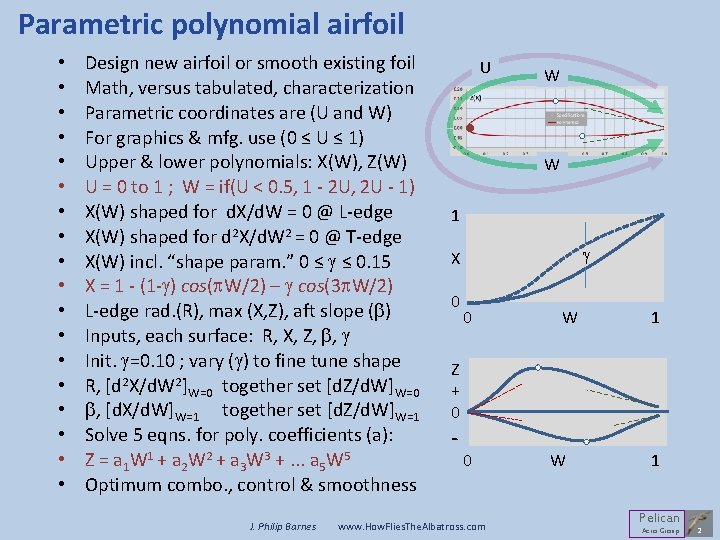
Parametric polynomial airfoil • • • • • Design new airfoil or smooth existing foil Math, versus tabulated, characterization Parametric coordinates are (U and W) For graphics & mfg. use (0 ≤ U ≤ 1) Upper & lower polynomials: X(W), Z(W) U = 0 to 1 ; W = if(U < 0. 5, 1 - 2 U, 2 U - 1) X(W) shaped for d. X/d. W = 0 @ L-edge X(W) shaped for d 2 X/d. W 2 = 0 @ T-edge X(W) incl. “shape param. ” 0 ≤ g ≤ 0. 15 X = 1 - (1 -g) cos(p. W/2) – g cos(3 p. W/2) L-edge rad. (R), max (X, Z), aft slope (b) Inputs, each surface: R, X, Z, b, g Init. g=0. 10 ; vary (g) to fine tune shape R, [d 2 X/d. W 2]W=0 together set [d. Z/d. W]W=0 b, [d. X/d. W]W=1 together set [d. Z/d. W]W=1 Solve 5 eqns. for poly. coefficients (a): Z = a 1 W 1 + a 2 W 2 + a 3 W 3 +. . . a 5 W 5 Optimum combo. , control & smoothness J. Philip Barnes U W W 1 g X 0 0 W 1 Z + 0 - 0 www. How. Flies. The. Albatross. com W 1 Pelican Aero Group 2

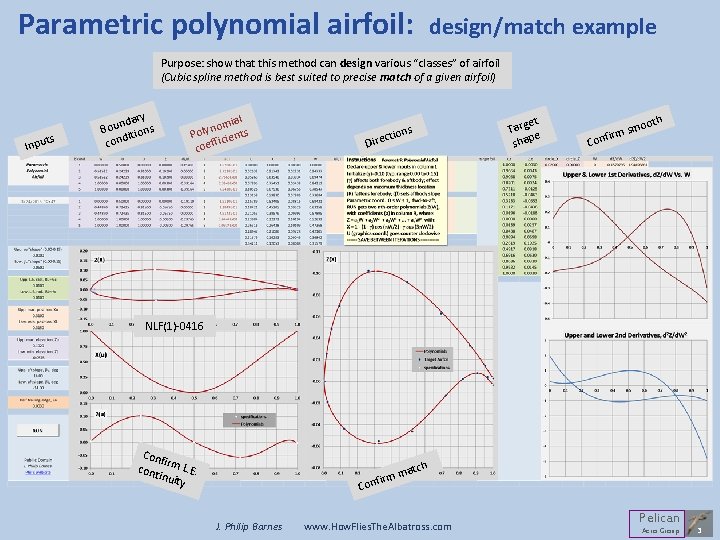
Parametric polynomial airfoil: design/match example Purpose: show that this method can design various “classes” of airfoil (Cubic spline method is best suited to precise match of a given airfoil) ts Inpu y ndar Bou tions i cond l omia s n y l Po icient f coef ions irect D et Targ e shap Co s nfirm th moo NLF(1)-0416 Conf i cont rm L. E. inuit y ch mat m r i onf C J. Philip Barnes www. How. Flies. The. Albatross. com Pelican Aero Group 3

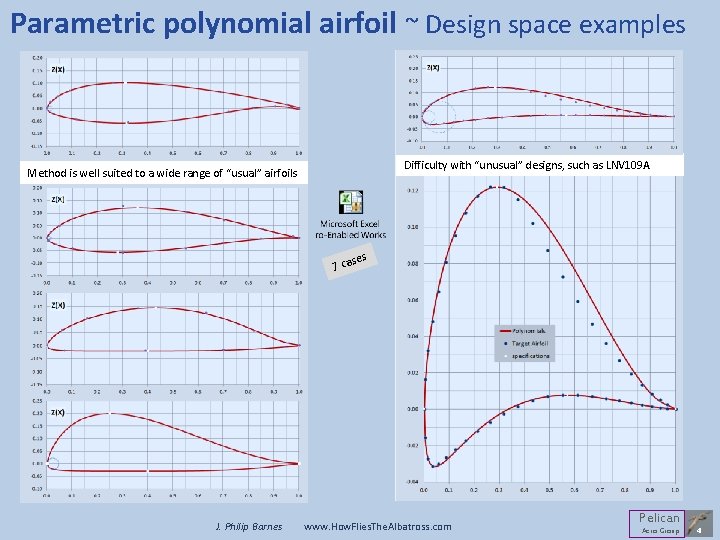
Parametric polynomial airfoil ~ Design space examples Difficulty with “unusual” designs, such as LNV 109 A Method is well suited to a wide range of “usual” airfoils ses 7 ca J. Philip Barnes www. How. Flies. The. Albatross. com Pelican Aero Group 4

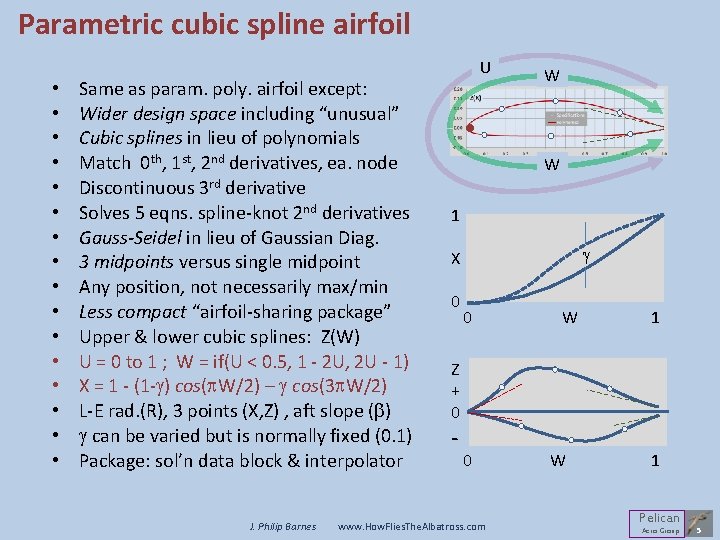
Parametric cubic spline airfoil • • • • Same as param. poly. airfoil except: Wider design space including “unusual” Cubic splines in lieu of polynomials Match 0 th, 1 st, 2 nd derivatives, ea. node Discontinuous 3 rd derivative Solves 5 eqns. spline-knot 2 nd derivatives Gauss-Seidel in lieu of Gaussian Diag. 3 midpoints versus single midpoint Any position, not necessarily max/min Less compact “airfoil-sharing package” Upper & lower cubic splines: Z(W) U = 0 to 1 ; W = if(U < 0. 5, 1 - 2 U, 2 U - 1) X = 1 - (1 -g) cos(p. W/2) – g cos(3 p. W/2) L-E rad. (R), 3 points (X, Z) , aft slope (b) g can be varied but is normally fixed (0. 1) Package: sol’n data block & interpolator J. Philip Barnes U W W 1 g X 0 0 W 1 Z + 0 - 0 www. How. Flies. The. Albatross. com W 1 Pelican Aero Group 5

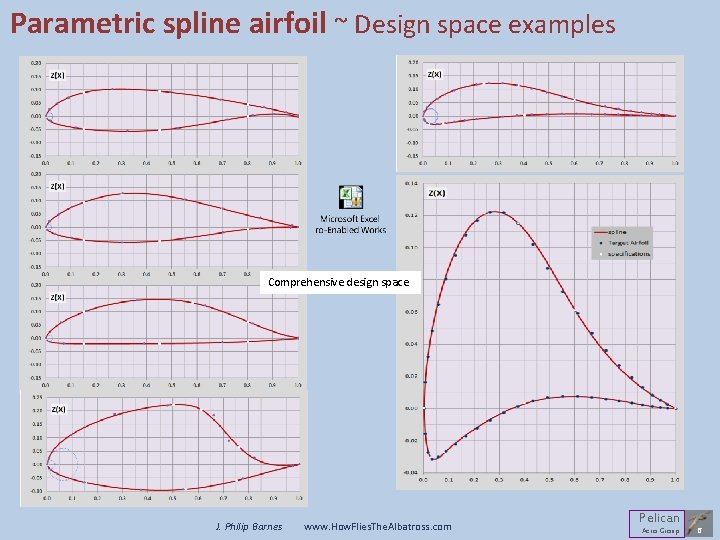
Parametric spline airfoil ~ Design space examples Comprehensive design space J. Philip Barnes www. How. Flies. The. Albatross. com Pelican Aero Group 6

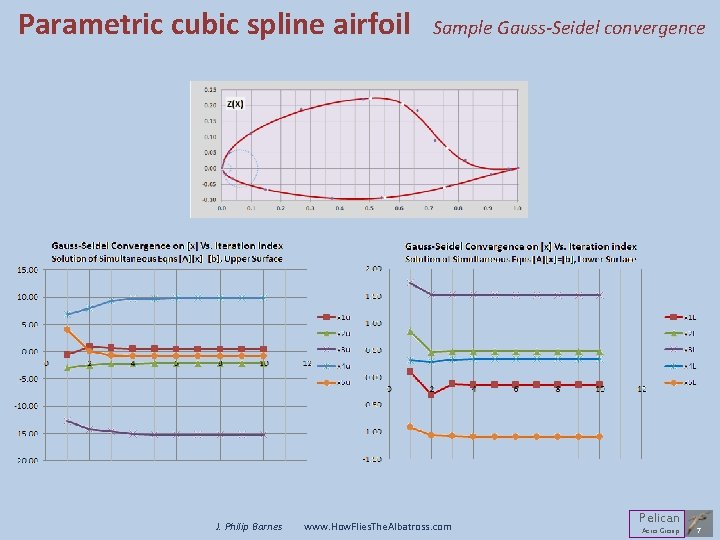
Parametric cubic spline airfoil J. Philip Barnes Sample Gauss-Seidel convergence www. How. Flies. The. Albatross. com Pelican Aero Group 7