POWER SYSTEM ANALYSIS EET 3083 1 EET 308

POWER SYSTEM ANALYSIS EET 308/3 1 EET 308 POWER SYSTEM ANALYSIS

CHAPTER 5 SYMMETRICA L COMPONENTS 2 EET 308 POWER SYSTEM ANALYSIS

On completion of this lesson, a student should be able to: Explain the important of symmetrical component. Construct positive sequence networks for a power system. Construct negative sequence networks for a power system. Construct zero sequence networks for a power system. 3 EET 308 POWER SYSTEM ANALYSIS

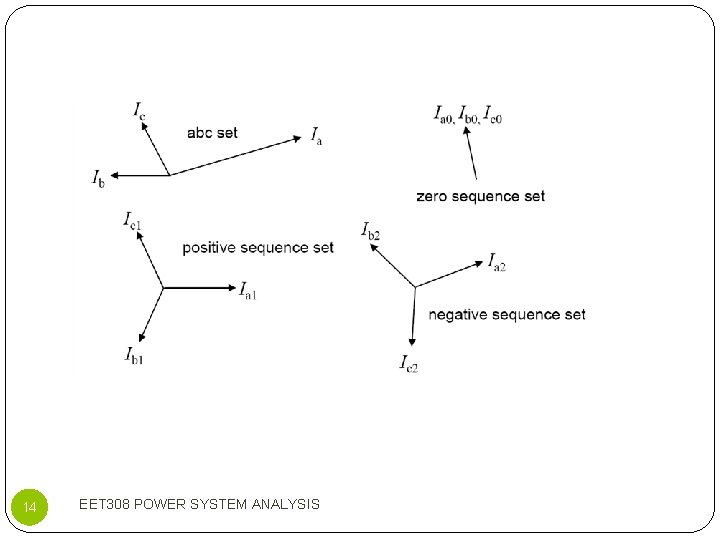
4. 1 INTRODUCTION Introduce by C. L Fortescue (1918) Allows unbalanced 3 phase phasor quantities to be replaced by the sum of 3 separate but balances symmetrical components: Applicable to current and voltage Permits modeling of unbalanced systems and networks 4 EET 308 POWER SYSTEM ANALYSIS

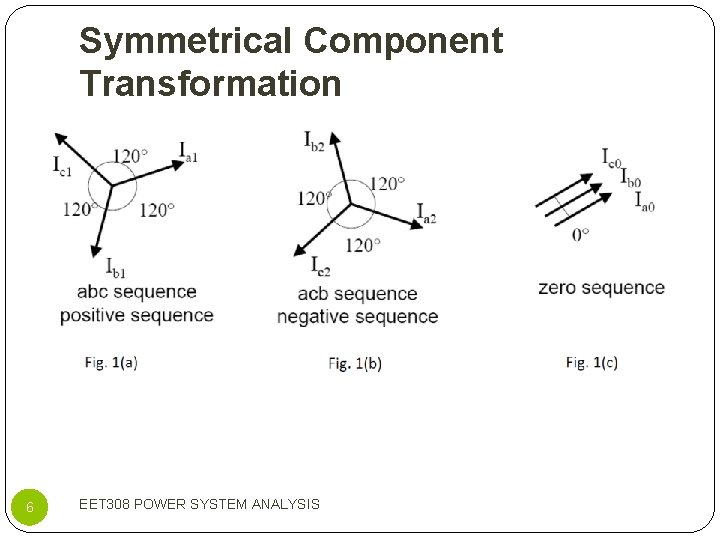
Symmetrical Component Transformation Representative symmetrical components; POS-SEQ: 3 phasors with equal magnitudes, ± 120° phase displacement and positive sequence NEG-SEQ: 3 phasors with equal magnitudes, ± 120° phase displacement and negative sequence ZERO-SEQ: 3 phasors with equal magnitudes and zero phase displacement 5 EET 308 POWER SYSTEM ANALYSIS

Symmetrical Component Transformation 6 EET 308 POWER SYSTEM ANALYSIS

Symmetrical Component Transformation Positive sequence phasors (refer Fig. 1(a)); Where operator a identities; 7 EET 102 ELECTRIC CIRCUIT II

Symmetrical Component Transformation Negative sequence phasor (refer Fig. 1(b)); Zero sequence phasor (refer Fig. 1(c)); 8 EET 308 POWER SYSTEM ANALYSIS

Symmetrical Component Transformation Relating unbalanced phasors to symmetrical components: In matrix notation: 9 EET 308 POWER SYSTEM ANALYSIS

Symmetrical Component Transformation [A] is known as the symmetrical components transformation matrix: Solving for the symmetrical components leads to : 10 EET 308 POWER SYSTEM ANALYSIS

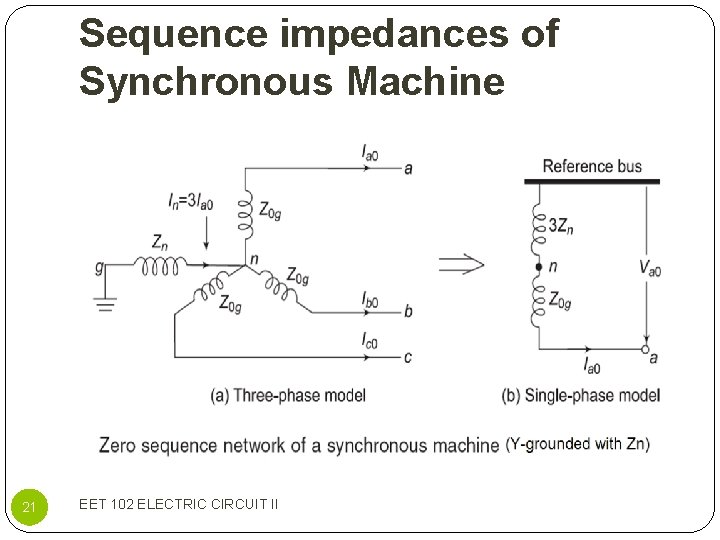
Symmetrical Component Transformation In component form, the calculation for symmetrical components are: From above, the zero-sequence component of current is equal to one-third of the sum of the phase currents. Therefore, when the phase currents sum to zero, e. g, in the 3 phase system with ungrounded neural, the zero sequence cannot exist. If the neutral of power system is grounded, zerosequence currents flows between the neutral and the ground. 11 EET 308 POWER SYSTEM ANALYSIS

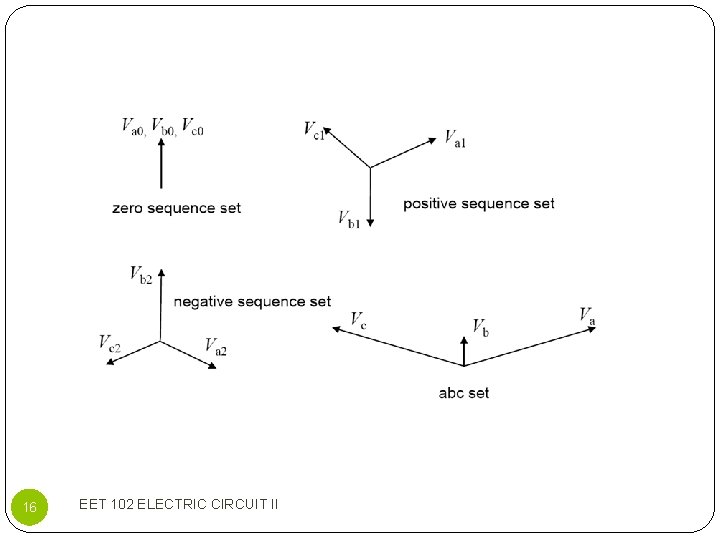
Symmetrical Component Transformation Similar expressions exist for voltages: The apparent power may also be expressed in terms of symmetrical components: 12 EET 308 POWER SYSTEM ANALYSIS

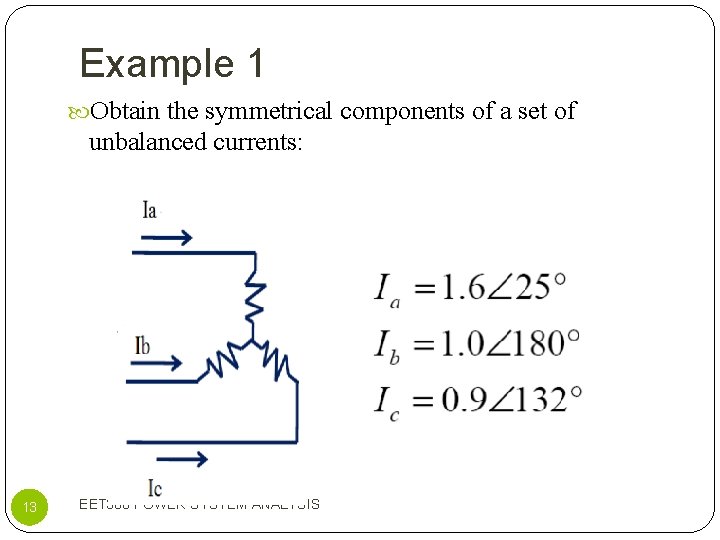
Example 1 Obtain the symmetrical components of a set of unbalanced currents: 13 EET 308 POWER SYSTEM ANALYSIS

14 EET 308 POWER SYSTEM ANALYSIS

Example 2 The symmetrical components of a set of unbalanced voltages are: Obtain the original unbalanced voltages. 15 EET 308 POWER SYSTEM ANALYSIS

16 EET 102 ELECTRIC CIRCUIT II

Sequence Impedances 17 EET 102 ELECTRIC CIRCUIT II

Sequence Impedances Augmented network models: Generators 3 -phase transformers Y-connected balanced loads # For this class, we will see the sequence impedance of Y-connected load only! 18 EET 102 ELECTRIC CIRCUIT II

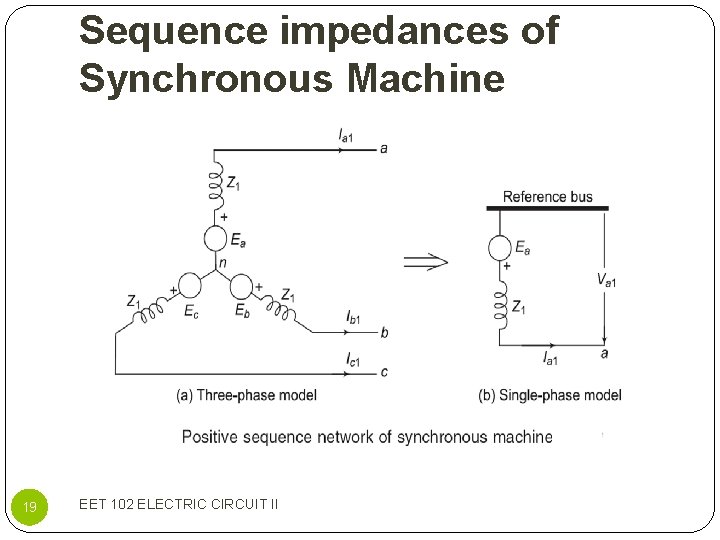
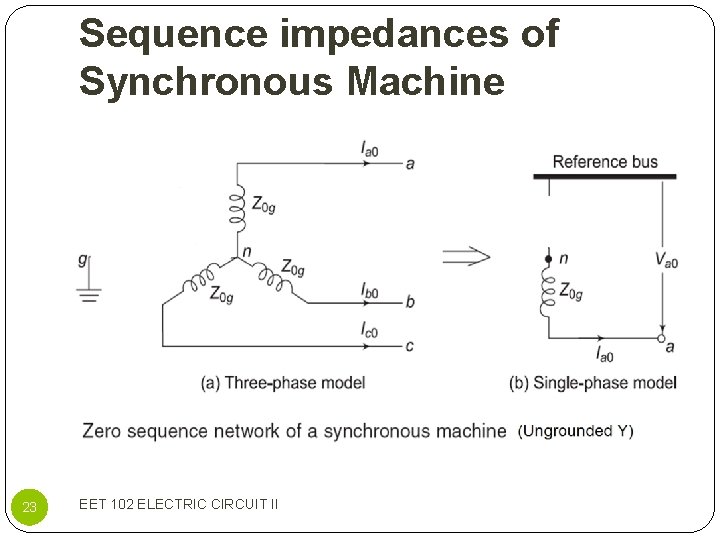
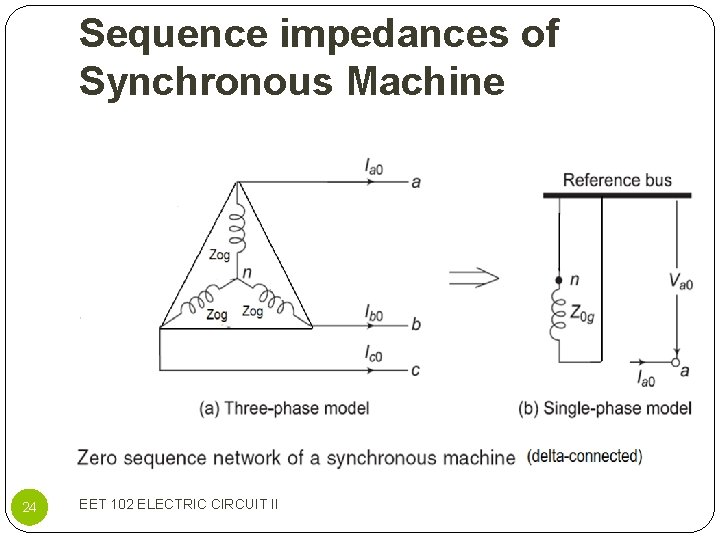
Sequence impedances of Synchronous Machine 19 EET 102 ELECTRIC CIRCUIT II

Sequence impedances of Synchronous Machine 20 EET 102 ELECTRIC CIRCUIT II

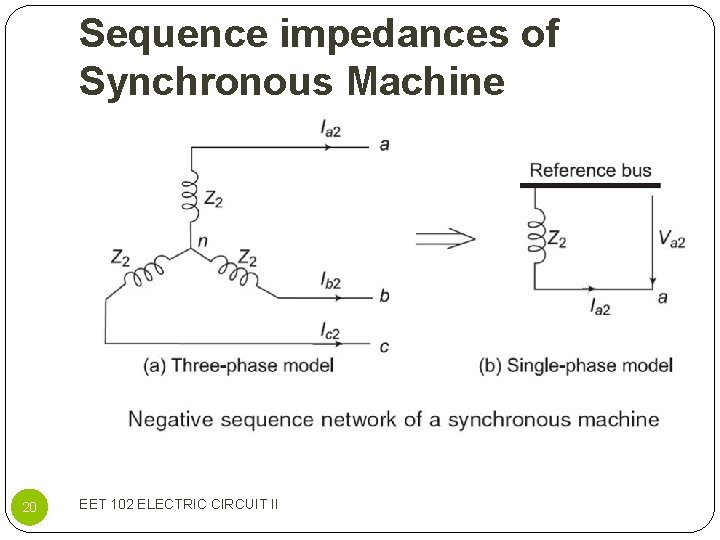
Sequence impedances of Synchronous Machine 21 EET 102 ELECTRIC CIRCUIT II

Sequence impedances of Synchronous Machine 22 EET 102 ELECTRIC CIRCUIT II

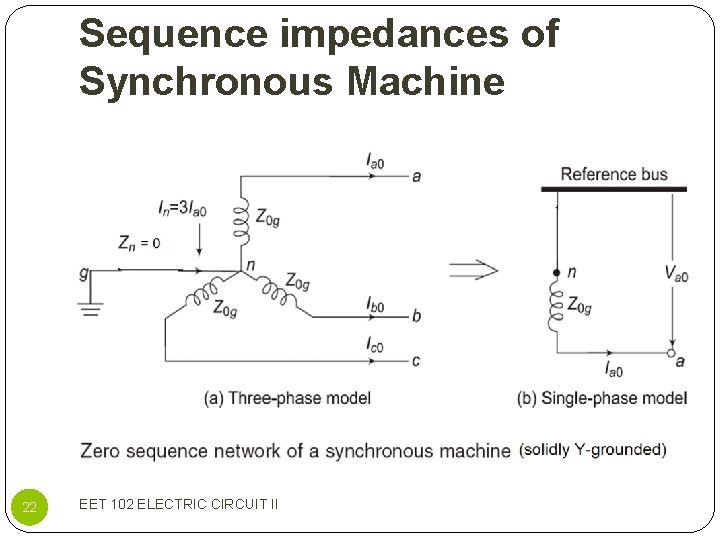
Sequence impedances of Synchronous Machine 23 EET 102 ELECTRIC CIRCUIT II

Sequence impedances of Synchronous Machine 24 EET 102 ELECTRIC CIRCUIT II

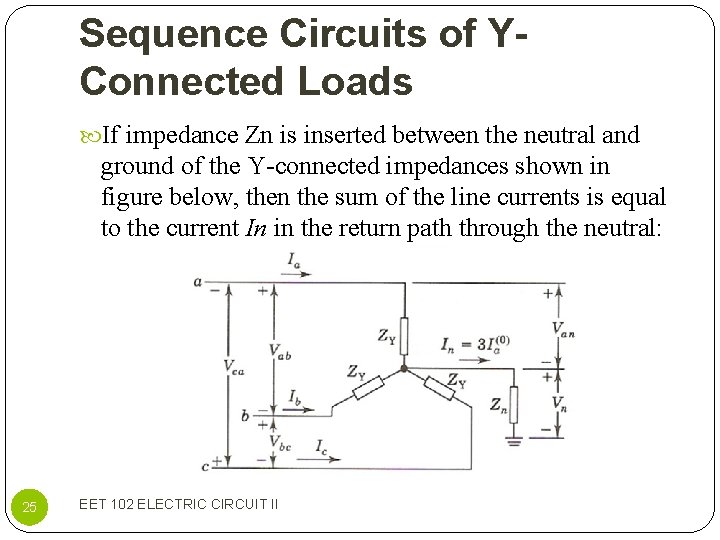
Sequence Circuits of YConnected Loads If impedance Zn is inserted between the neutral and ground of the Y-connected impedances shown in figure below, then the sum of the line currents is equal to the current In in the return path through the neutral: 25 EET 102 ELECTRIC CIRCUIT II

Connected Loads Expressing the unbalanced line currents in term of their symmetrical components gives: Since the +ve sequence and –ve sequence currents added separately to zero at neutral point n, there cannot be any +ve sequence and –ve sequence currents in the connections from neutral to ground regardless of the value of Zn. 26 EET 102 ELECTRIC CIRCUIT II

Connected Loads 27 EET 102 ELECTRIC CIRCUIT II

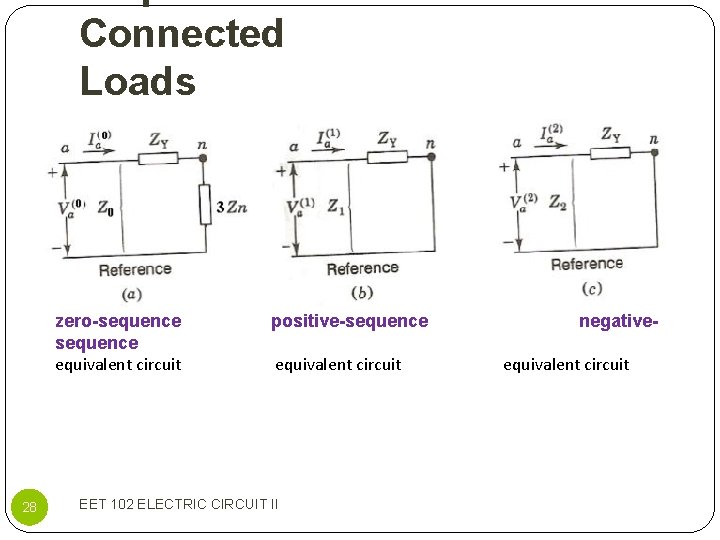
Connected Loads zero-sequence equivalent circuit 28 positive-sequence equivalent circuit EET 102 ELECTRIC CIRCUIT II negativeequivalent circuit

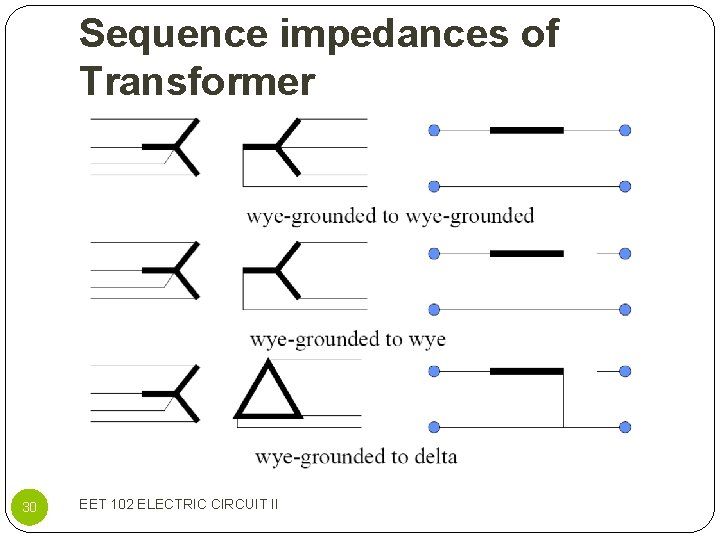
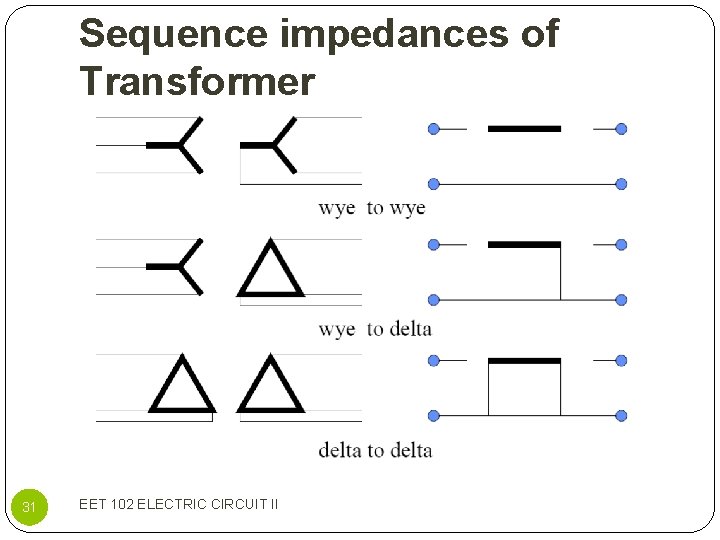
Sequence impedances of Transformer 29 EET 102 ELECTRIC CIRCUIT II

Sequence impedances of Transformer 30 EET 102 ELECTRIC CIRCUIT II

Sequence impedances of Transformer 31 EET 102 ELECTRIC CIRCUIT II

Construction of Sequence Networks of A Power System Complete sequence networks of a power system can be constructed by using all the sequence networks discussed before; synchronous machines, transformer and lines. Start with one-line diagram with respect to impedances; POS-SEQ – has synchronous machine (generators & 32 motors) in the sequence network. NEG-SEQ –has same sequence network like POS-SEQ but it has zero voltages. ZERO-SEQ- combine all the zero sequence networks of SMs, transformers and lines. No voltage sources present EET 102 ELECTRIC CIRCUIT II in the sequence.

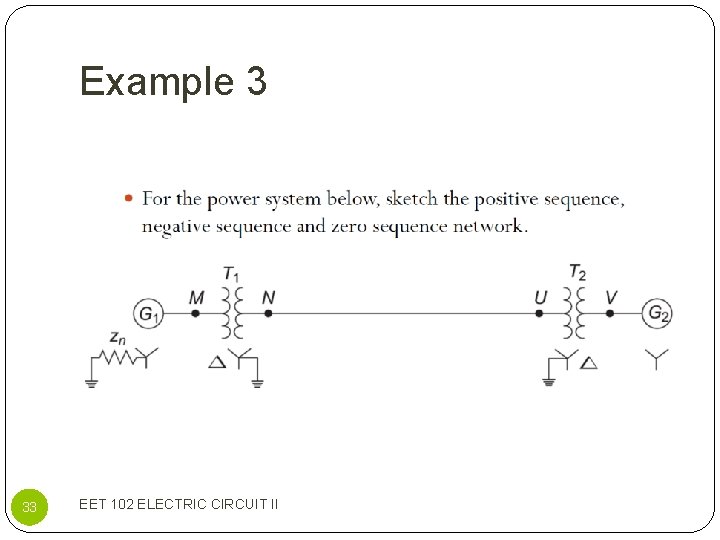
Example 3 33 EET 102 ELECTRIC CIRCUIT II