Power Point Slides for Financial Institutions Markets and

Power Point Slides for: Financial Institutions, Markets, and Money, 9 th Edition Authors: Kidwell, Blackwell, Whidbee & Peterson Prepared by: Babu G. Baradwaj, Towson University And Lanny R. Martindale, Texas A&M University Copyright© 2006 John Wiley & Sons, Inc. 1

CHAPTER 5 BOND PRICES AND INTEREST RATE RISK Copyright© 2005 John Wiley & Sons, Inc

The Time Value of Money: Investing—in financial assets or in real assets—means giving up consumption until later. Positive time preference for consumption must be offset by adequate return. Opportunity cost of deferring consumption determines minimum rate of return required on a risk-free investment— Present sums are theoretically invested at not less than this rate; Future cash flows are discounted by at least this rate. Time value of money has nothing primarily to do with inflation. Inflation expectations affect discount rate, but Deferred consumption has opportunity cost by definition. Copyright© 2006 John Wiley & Sons, Inc. 3

Future Value or Compound Value The future value (FV) of a sum (PV) is FV = PV (1+i)n where i is the periodic interest rate and n is the number of compounding periods. Copyright© 2006 John Wiley & Sons, Inc. 4

Present Value The value now of a sum expected at a future time is given by With risk present, a premium may be added to the riskfree rate. The higher the discount rate, the lower the present value. Copyright© 2006 John Wiley & Sons, Inc. 5

Bond Pricing: What is a bond? A form of loan—a debt security obligating a borrower to pay a lender principal and interest. Borrower (issuer) promises contractually to make periodic payments to lender (investor or bondholder) over given number of years At maturity, holder receives principal (or face value or par value). Periodically before maturity, holder receives interest (coupon) payments determined by coupon rate, original interest rate promised as percentage of par on face of bond. Copyright© 2006 John Wiley & Sons, Inc. 6

What is a bond? Example Par value Coupon Rate Issued Matures $1, 000 5% Today 30 years from today Scheduled Payments: $50/year interest for 30 years $1, 000 par at end of year 30 Copyright© 2006 John Wiley & Sons, Inc. 7

Bond Pricing: bond cash flows Bondholder thus owns right to a stream of cash flows: Ordinary annuity of interest payments and Future lump sum in return of par value, Discountable to a present value at any time while bond is outstanding. Copyright© 2006 John Wiley & Sons, Inc. 8

Bond Pricing: Present Value The value (price) of a bond is the present value of the future cash flows promised, discounted at the market rate of interest (the required rate of return on this risk class in today’s market) Copyright© 2006 John Wiley & Sons, Inc. 9

PV of bond cash flows Where PB = price of bond or present value of promised payments; Ct = coupon payment in period t, where t = 1, 2, 3, …, n; Fn = par value (principal amount) due at maturity; i = market interest rate (discount rate or market yield); and n = number of periods to maturity. Copyright© 2006 John Wiley & Sons, Inc. 10

Bond pricing: principles Cash flows are assumed to flow at end of the period and to be reinvested at i. Bonds typically pay interest semiannually. Increasing i decreases price (PB); decreasing i increases price; thus bond prices and interest rates move inversely. If market rate equals coupon rate, bond trades at par. If coupon rate exceeds market rate, the bond trades above par—at a premium. If market rate exceeds coupon rate, bond trades below par —at a discount. Copyright© 2006 John Wiley & Sons, Inc. 11

Zero coupon bonds are “pure discount” instruments. No periodic coupon payments. Issued at discount from par. Single payment of par value at maturity. PB is simply PV of FV represented by par value, discounted at market rate. Copyright© 2006 John Wiley & Sons, Inc. 12

Bond yields: risks rewarded Yield rewards investor for at least 3 risks: Credit or default risk: chance that issuer may be unable or unwilling to pay as agreed. Reinvestment risk: potential effect of variability of market interest rates on return at which payments can be reinvested when received. Price risk: Inverse relationship between bond prices and interest rates. Copyright© 2006 John Wiley & Sons, Inc. 13

Bond yields: set by market Discount rate at which bond price equals discounted PV of expected payments. Measure of return ideally capturing impact of Coupon payments Income from reinvestment of coupons Any capital gain or loss Copyright© 2006 John Wiley & Sons, Inc. 14

Common yield measures Yield to maturity Realized yield Expected yield Copyright© 2006 John Wiley & Sons, Inc. 15

Yield to maturity Investor's expected yield if bond is held to maturity and all payments are reinvested at same yield. Normally determined by iteration—try different discount rates until PB=present value of future payments. The longer until maturity, the less valid the reinvestment assumption. Copyright© 2006 John Wiley & Sons, Inc. 16

Computing yield to maturity Investor buys 5% percent coupon (semiannual payments) bond for $951. 90; bond matures in 3 years. Solve the bond pricing equation for the interest rate (i) such that price paid for the bond equals PV of remaining payments due under the bond. Copyright© 2006 John Wiley & Sons, Inc. 17

Computing yield to maturity, cont. Solving either by trial and error or with a financial calculator results in yield to maturity of 3. 4% semiannually, or 6. 8% annually. Copyright© 2006 John Wiley & Sons, Inc. 18

Realized yield Investor’s ex post or “hindsight” actual rate of return, given the cash flows actually received and their timing. May differ from YTM due to— change in the amount or timing of promised payments (e. g. default). change in market interest rates affecting reinvestment rate. sale of bond before maturity at premium or discount. Copyright© 2006 John Wiley & Sons, Inc. 19

Computing Realized Yield Investor pays $1, 000 for 10 -year 8% coupon bond; sells bond 3 years later for $902. 63. Solve for i such that $1, 000 (the original investment) equals PV of 2 annual payments of $80 followed by a 3 rd annual payment of $982. 63 (the actual cash flows this investor received). Copyright© 2006 John Wiley & Sons, Inc. 20

Computing realized yield, cont. Solving either by trial and error or with a financial calculator results in a realized yield of 4. 91%. Copyright© 2006 John Wiley & Sons, Inc. 21

Expected yield Predicted yield for a given holding period. Must forecast— Expected interest rate(s) Bond price at end of holding period Plug forecast results into bond pricing formula Copyright© 2006 John Wiley & Sons, Inc. 22

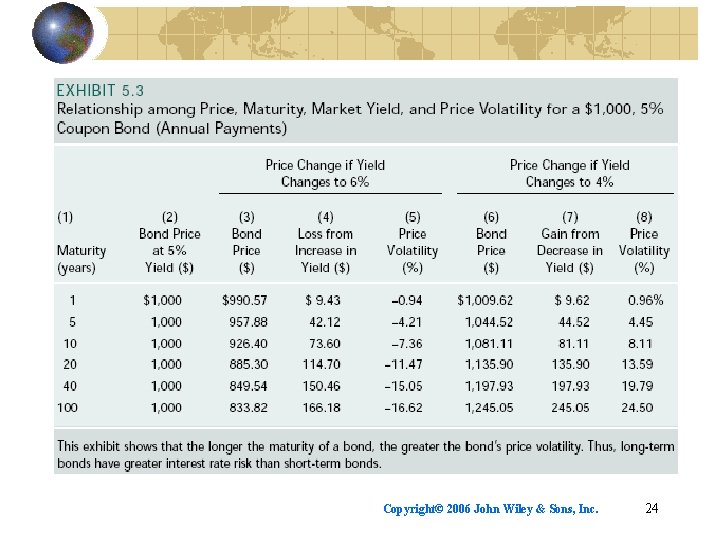
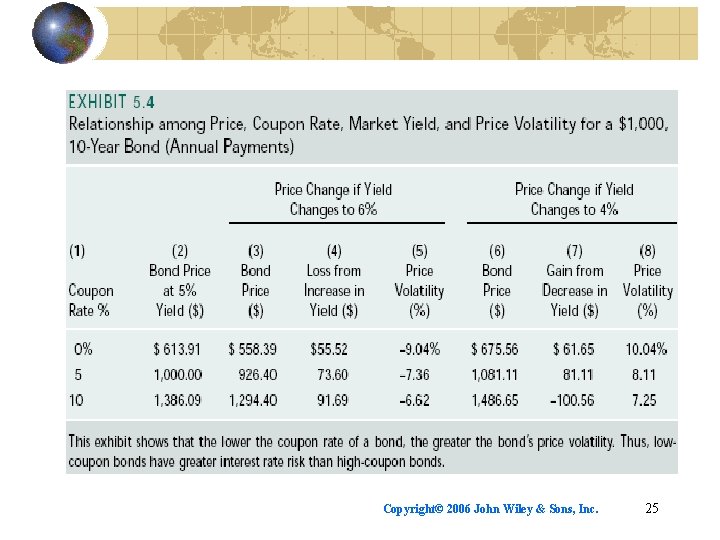
Bond price volatility (price risk) Percentage change in price for given change in interest rates: where %∆PB = percentage change in price Pt = new price in period t P t – 1 = bond’s price one period earlier Copyright© 2006 John Wiley & Sons, Inc. 23

Copyright© 2006 John Wiley & Sons, Inc. 24

Copyright© 2006 John Wiley & Sons, Inc. 25

Copyright© 2006 John Wiley & Sons, Inc. 26

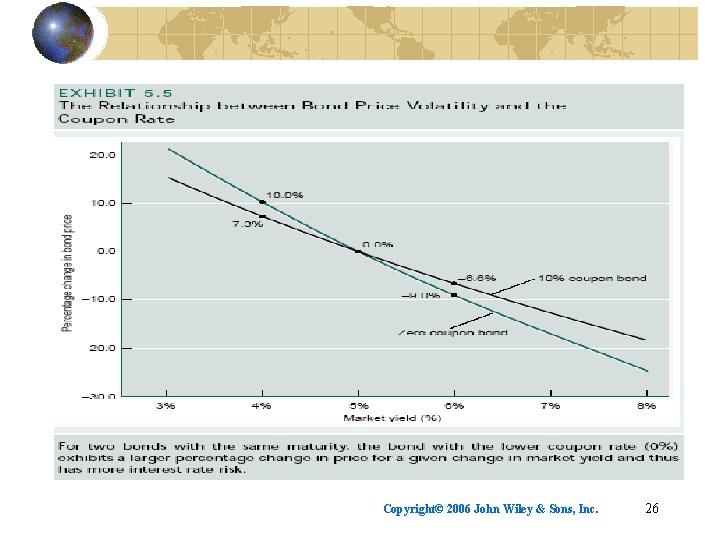
Bond theorems Bond prices are inversely related to bond yields. The price volatility of a long-term bond is greater than that of a short-term bond, holding the coupon rate constant. The price volatility of a low-coupon bond is greater than that of a high-coupon, bond, holding maturity constant Copyright© 2006 John Wiley & Sons, Inc. 27

Interest Rate Risk and Duration Price Risk Reinvestment Risk Duration as a risk management tool Copyright© 2006 John Wiley & Sons, Inc. 28

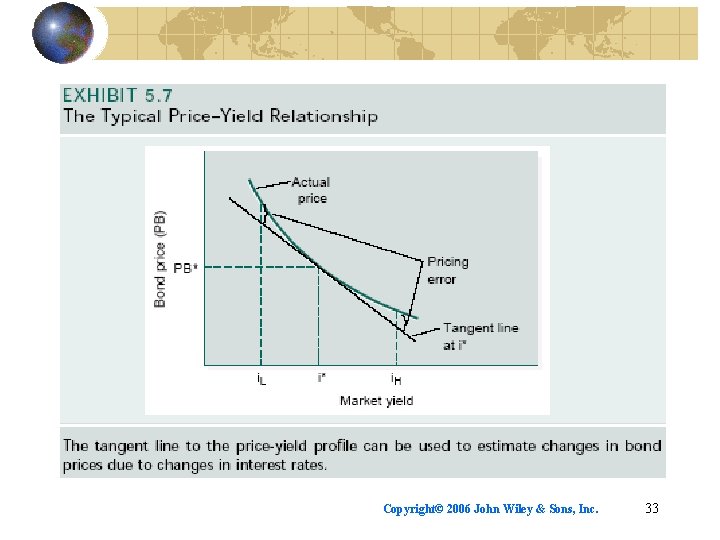
Interest rate risk comprises price risk and reinvestment risk. Price risk is the variability in bond prices caused by their inverse relationship with interest rates. Reinvestment risk is the variability in realized yield caused by changing market rates at which coupons can be reinvested. Price risk and reinvestment risk work against each other. As interest rates fall — • Bond prices rise but • Coupons are reinvested at lower return. As interest rates rise— • Bond prices fall but • Coupons are reinvested at higher return. Copyright© 2006 John Wiley & Sons, Inc. 29

Duration - a measure of interest rate risk Macaulay’s Duration where: D = duration of the bond CFt = interest or principal payment at time t t = time period in which payment is made n = number of periods to maturity i = the yield to maturity (interest rate) Copyright© 2006 John Wiley & Sons, Inc. 30

Duration concepts (all else equal): Higher coupon rates mean shorter duration and less price volatility. Duration equals term to maturity for zero coupon securities. Longer maturities mean longer durations and greater price volatility. The higher the market rate of interest, the shorter the duration. Copyright© 2006 John Wiley & Sons, Inc. 31

Duration can be calculated for an entire portfolio where: wi = proportion of bond i in portfolio and Di = duration of bond i. Copyright© 2006 John Wiley & Sons, Inc. 32

Copyright© 2006 John Wiley & Sons, Inc. 33

Using Duration to Measure & Manage Interest Rate Risk Duration is the holding period for which reinvestment risk just offsets price risk: the holder obtains the original, promised yield to maturity. Financial institutions use duration to manage interest rate risk and actually achieve the desired yield for the desired holding period. Zero-coupon approach: zero-coupon bonds have no reinvestment risk. The duration of a “zero” equals its term to maturity. Buy a “zero” with the desired holding period and lock in the YTM. Must hold to maturity to evade price risk. Duration matching: To realize yield to maturity, investors select bonds with durations matching their desired holding periods. Maturity matching: Selecting a term to maturity equal to the desired holding period eliminates price risk, but not reinvestment risk. Copyright© 2006 John Wiley & Sons, Inc. 34