Power and Sample Size in Testing One Mean

Power and Sample Size in Testing One Mean 1

Type I & Type II Error • Type I Error: reject the null hypothesis when it is true. The probability of a Type I Error is denoted by . • Type II Error: accept the null hypothesis when it is false and the alternative hypothesis is true. The probability of a Type II Error is denoted by . 2

Null hypothesis Decision True False Reject H 0 Type I Error Correct Decision 1 Do not reject H 0 Correct Decision 1 Type II Error 3

A Population The serum cholesterol levels for all 20 to 24 -year-old males of a certain population was claimed to be normally distributed with a mean of 180 mg/100 ml and standard deviation is 46 mg/100 ml. 4

Research Hypothesis Is the mean cholesterol level of the population of 20 - to 74 -year-olds higher than 180 mg/100 ml ? H 0: = 180 mg/100 ml (or 180 mg/100 ml) Ha: > 180 mg/100 ml 5

Power of the Test 6

Power of the Test The power of the statistical test is the ability of the study as designed to distinguish between the hypothesized value and some specific alternative value. That is, the power is the probability of rejecting the null hypothesis if the null hypothesis is false. Power = P(reject H 0 | H 0 is false) Power = 1 The power is usually calculated given a simple alternative hypothesis: Ha: = 211 mg/100 ml Power = P(reject H 0 | Ha is true) 7

Assuming that we use a sample of size 25 and test the hypothesis with a level of significant = 0. 05, what would be the and the power of the test, i. e. 1 ? If we take the critical value approach, the critical value would be 1. 645. At the level of significant = 0. 05, we would reject H 0 if z 1. 645. Rejection region Right tail area is 0. 05 z 0 1. 645 8

If a sample of size 25 is selected, what would be the critical value in terms of the mean cholesterol level? Rejection region Right tail area is 0. 05 0 1. 645 z Rejection region 180 195. 1 ? 9

If the alternative hypothesis Ha: = a = 211 mg/100 ml, what would be the probability of NOT rejecting H 0, i. e. ? H 0: = 0 = 180 v. s. Ha: = = 211 That is to say “how powerful can this test detect a 31 mg/100 ml increase in average cholesterol level? ” 180 195. 1 211 = ? 0. 042 Power of the test when sample size is 25: Power = 1 – 0. 042 = 0. 958. 10

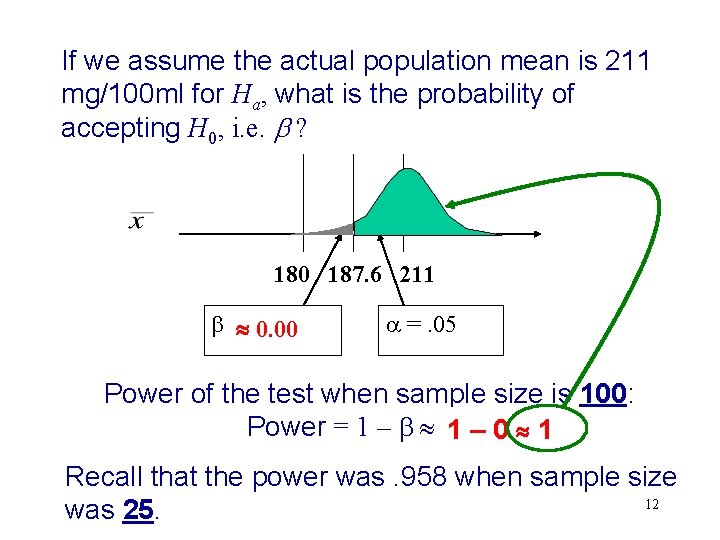
Assuming that we use a sample of size 100 and test the hypothesis with a level of significant = 0. 05, what would be the and the power of the test, i. e. 1 ? Rejection region z Right tail area is 0. 05 0 1. 645 Rejection region 180 187. 6 ? 11

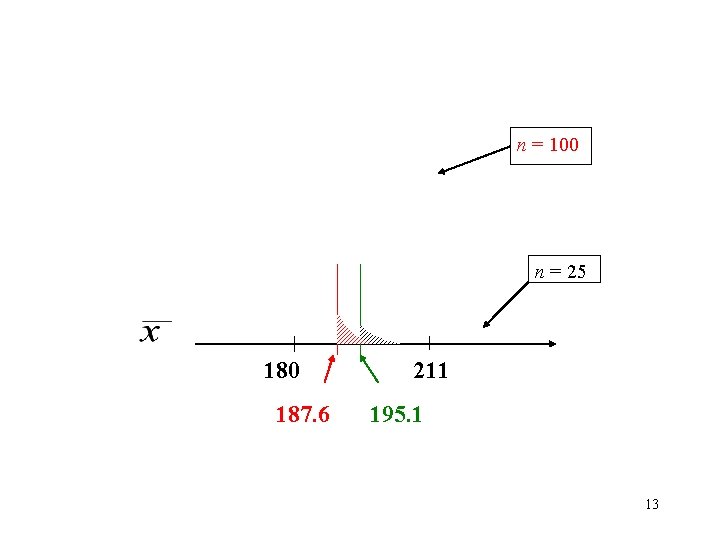
If we assume the actual population mean is 211 mg/100 ml for Ha, what is the probability of accepting H 0, i. e. ? 180 187. 6 211 = ? 0. 00 =. 05 Power of the test when sample size is 100: Power = 1 – ? 1 – 0 1 Recall that the power was. 958 when sample size 12 was 25.

n = 100 n = 25 180 187. 6 211 195. 1 13

Sample Size Estimation 14

H 0: = 180 mg/100 ml (or 180 mg/100 ml) v. s. HA: > 180 mg/100 ml, to perform a test at the power level of 0. 95, with the level of significance of 0. 01, how large a sample do we need? (Power of 0. 95 means we want to risk a 5% chance of failing to reject the null hypothesis if the true mean is as large as 211 mg/100 ml. Or, to say, we want to have a 95% chance of rejecting the null hypothesis if the true mean is as large as 211 mg/100 ml. ) 15

180 = 0. 05 211 =. 01 16

Let the unknown sample size to be n. If =. 01, then the critical value in z-score would be 2. 32. The critical value in average cholesterol level would be If the true mean is 211 mg/100 ml, with a power of 0. 95, i. e. =. 05, we would accept the null hypothesis when the sample average is less than 118 = 0. 05 211 =. 01 17

118 211 Set the two equations equal to each other: Solve for n: So, the sample size needed is 35. 18

Formula: The estimated sample size for a onesided test with level of significance and a power of 1 to detect a difference of a – 0 is, 19

For a two-sided test, the formula is 20

Example: For testing hypothesis that H 0: = 0 = 70 v. s. (Two-sided Test) Ha: 70 with a level of significance of =. 05. Find the sample size so that one can have a power of 1 =. 90 to reject the null hypothesis if the actual mean is a = 80. The standard deviation, s, is approximately equal 15. 21

=. 05 1 =. 90 =. 10 z /2 = z. 025 = 1. 96 z = z. 1 = 1. 28 The sample size needed is 24. 22

Example: For testing hypothesis that H 0: = 0 = 70 v. s. Ha: < 70 (One-sided Test) with a level of significance of =. 05. Find the sample size so that one can have a power of 1 =. 95 to reject the null hypothesis if the actual mean is a = 60 (or the actual difference in means is 10). The standard deviation, s, is approximately equal 15. 23

Example: For testing hypothesis that H 0: = 0 = 70 v. s. Ha: 70 (Two-sided Test) with a level of significance of =. 05. Find the sample size so that one can have a power of 1 =. 95 to reject the null hypothesis if the actual mean is a = 75. The standard deviation, s, is approximately equal 15. 24