Power and sample size calculations Michael Vth University

Power and sample size calculations Michael Væth, University of Aarhus • Introductory remarks • Two-sample problem with normal data • Comparison of two proportions • Sample size and power calculations based on Wald’s test • Two-sample problem with censored survival data • Non-inferiority trials and equivalence trials • Sample size and confidence intervals November 10, 2010 DSTS meeting, Copenhagen 1

Power and sample size calculations “Investigators often ask statisticians how many observations they should make (fortunately, usually before the study begins). To be answerable, this question needs fuller formulation. There is resemblance to the question, How much money should I take when I go on vacation? Fuller information is needed there too. How long a vacation? Where? With whom? ” Moses(NEJM, 1985) November 10, 2010 DSTS meeting, Copenhagen 2

Power and sample size calculations A study should: ØAllow conclusive answers to the questions being addressed ØProvide estimates of relevant quantities with sufficient precision Standard approach Identify a maximal risk of wrong conclusions or Quantify the size of a sufficient precision Determine the minimum sample size for which the study achieves the design goals November 10, 2010 DSTS meeting, Copenhagen 3

Power and sample size calculations Implementation of standard approach Use commercial special-purpose software Simulations Analytic methods November 10, 2010 DSTS meeting, Copenhagen 4

Two-sample problem with continuous outcome RCT, equal allocation probabilities Outcome follow a normal distribution. Means Common standard deviation, assumed known: Expected treatment difference Minimal relevant difference Estimated treatment difference: Hypothesis: Test statistic: November 10, 2010 DSTS meeting, Copenhagen 5

Two-sample problem with continuous outcome (2) If the test statistic has a standard normal distribution. In general, the test statistic is normal: mean and standard deviation 1 November 10, 2010 DSTS meeting, Copenhagen 6

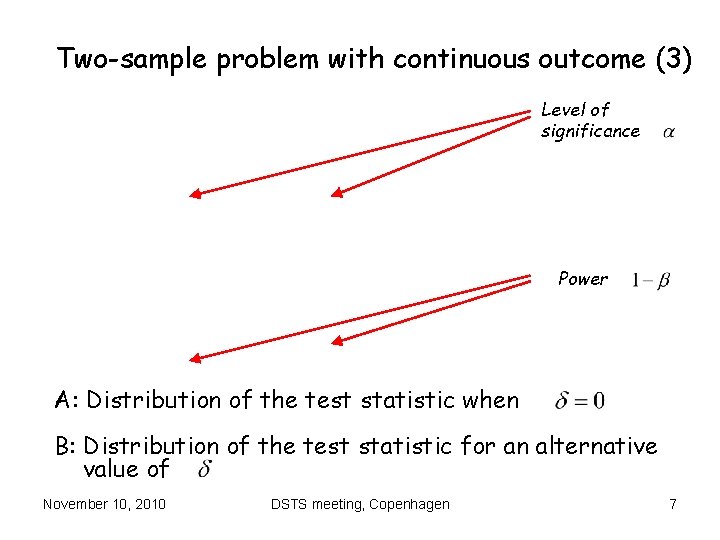
Two-sample problem with continuous outcome (3) Level of significance Power A: Distribution of the test statistic when B: Distribution of the test statistic for an alternative value of November 10, 2010 DSTS meeting, Copenhagen 7

Two-sample problem with continuous outcome (4) Only contribution from one term unless power close to level of significance Assume so only the upper term matters Basic relation November 10, 2010 DSTS meeting, Copenhagen 8

Two-sample problem with continuous outcome (5) Sample size for given power Power for given sample size November 10, 2010 DSTS meeting, Copenhagen 9

Two-sample problem with continuous outcome (6) Depends on the error probabilities Depend on the problem Table of for selected values of Level of November 10, 2010 Statistical power significance 50% 80% 95% 5% 3. 84 7. 85 10. 51 12. 99 2. 5% 5. 02 9. 51 12. 41 15. 10 1% 6. 63 11. 68 14. 88 17. 81 0. 5% 7. 88 13. 31 16. 72 19. 82 DSTS meeting, Copenhagen 10

Comparison of two proportions Score test: Basic relation becomes with November 10, 2010 DSTS meeting, Copenhagen 11

Comparison of two proportions (2) Wald’s test: Basic relation becomes The simple structure N = (model term)(error term) is recovered November 10, 2010 DSTS meeting, Copenhagen 12

Comparison of two proportions (3) Example 1 N(Score) = 2894 N(Wald) = 2888 Other sample fractions N(Score) = 4610 N(Score) = 4422 N(Wald) = 4278 N(Wald) = 4749 November 10, 2010 DSTS meeting, Copenhagen 13

Sample size and power calculations based on Wald’s test Data and Statistical model Question: Hypothesis about 1 -dim. parameter Wald’s test with Sample size for given power Power for given sample size November 10, 2010 DSTS meeting, Copenhagen 14

Sample size and power calculations based on Wald’s test (2) Example 1 (ctd. ) Same problem, but now use Wald’s test based on ln(odds) Score Wald November 10, 2010 N = 2906 2894 2888 N = 4778 4610 4278 N = 4304 4422 4749 DSTS meeting, Copenhagen 15

Sample size and power calculations based on Wald’s test (3) Use of simulations Computer generates a large number of independent sample of size from a scenario representing a relevant difference Power estimated as proportion of samples for which Wald’s test is statistically significant at level Sample size for power level November 10, 2010 DSTS meeting, Copenhagen 16

Sample size and power calculations based on Wald’s test (4) Use of simulations Sample size multiplier November 10, 2010 DSTS meeting, Copenhagen 17

Two-sample problem with censored survival data Time-to-event data Two sample, proportional hazards model Hazard rates Parameter of interest Wald’s test with the number of events in group i November 10, 2010 DSTS meeting, Copenhagen 18

Two-samples with censored data (2) Wald’s test is approximately normal with sd = 1 and mean average probability of an event in group i Sample size depends primarily on number of events November 10, 2010 DSTS meeting, Copenhagen 19

Two-samples with censored data (3) Example 2 Design of a RCT with survival endpoint Comparison of new and standard treatment Endpoint: All-cause mortality Requirements: max. 6 years; power = 80% for HR = 0. 8 Study start Accrual ends 0 Accrual period No additional follow-up November 10, 2010 Study ends A T=A+F Follow-up period In general DSTS meeting, Copenhagen 20

Two-samples with censored data (3) Example 2 (ctd. ) KM-estimate: standard treatment 1 - KM Std. Treatment: Average event probability = AUC/baseline Average event probability with new treatment November 10, 2010 DSTS meeting, Copenhagen 21

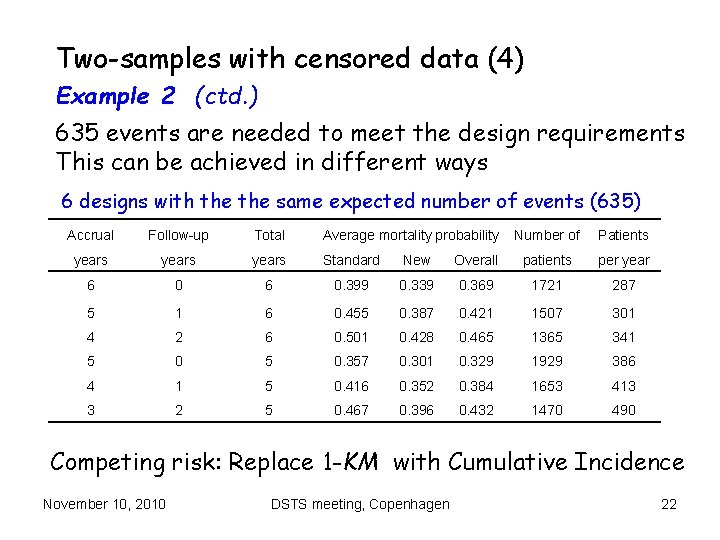
Two-samples with censored data (4) Example 2 (ctd. ) 635 events are needed to meet the design requirements This can be achieved in different ways 6 designs with the same expected number of events (635) Accrual Follow-up Total Average mortality probability Number of Patients years Standard New Overall patients per year 6 0. 399 0. 339 0. 369 1721 287 5 1 6 0. 455 0. 387 0. 421 1507 301 4 2 6 0. 501 0. 428 0. 465 1365 341 5 0. 357 0. 301 0. 329 1929 386 4 1 5 0. 416 0. 352 0. 384 1653 413 3 2 5 0. 467 0. 396 0. 432 1470 490 Competing risk: Replace 1 -KM with Cumulative Incidence November 10, 2010 DSTS meeting, Copenhagen 22

Non-inferiority & equivalence trials Minimal relevant difference Maximal irrelevant difference Null hypothesis November 10, 2010 DSTS meeting, Copenhagen 23

Non-inferiority & equivalence trials Two-sample problem with normal data (Wald’s test approach for 1 -parameter problem) Non-inferiority: a one-sided hypothesis Basic relation Sample size Note: If the power is assessed at a zero difference, then the sample size needed to achieve this power will be underestimated if the effect of the new product is less than that of the active control November 10, 2010 DSTS meeting, Copenhagen 24

Non-inferiority & equivalence trials Equivalence: union-intersection test Two one-sided tests Basic relations Sample size: is specified for Note: If the power is assessed at a zero difference, then the sample size needed to achieve this power is underestimated if the true difference is not zero. November 10, 2010 DSTS meeting, Copenhagen 25

Sample size and confidence intervals Design phase: Sample size considerations are traditionally phrased in the terminology of hypothesis testing Formulas are derived by controlling error probabilities Reporting and interpreting results Focus on estimates and confidence intervals Hypothesis tests are downplayed Why not use the same approach on both occasions? November 10, 2010 DSTS meeting, Copenhagen 26

Sample size and confidence intervals Power calculations when reporting the results? Probability statements should utilize the collected data and not be based on anticipated values of the parameters. Some statistical packages provide calculation of ”post-hoc power” or ”observed power”, i. e. Power computed at the estimated parameter value. This does not make sense. The power becomes a (known) function of the significance level. Interpretation: Probability of replication November 10, 2010 DSTS meeting, Copenhagen 27

Sample size and confidence intervals Sample size calculations based on confidence intervals? Two-sample problem with normal data (Wald’s test approach for 1 -parameter problem) 95% confidence interval Choose smallest N such that a confidence interval centered at excludes 0 Corresponds to power = 0. 50 November 10, 2010 DSTS meeting, Copenhagen 28

Sample size and confidence intervals Use the fundamental relation between hypothesis test and confidence intervals to formulate the sample size requirements in confidence interval terminology Greenland(AJE, 1988), Daly(BMJ, 1991) To compute a sample size specify 1. The confidence level 2. The minimum size parameter-value that we wish to estimate unambigously, i. e. with a confidence interval that excluded the null value 3. The probability of achieving this if the true value is the this minimum value November 10, 2010 DSTS meeting, Copenhagen 29

Power and sample size calculations A ”commentary” on the world-wide-web: "How not to collaborate with a biostatistician” http: //www. xtranormal. com/watch/6878253/ November 10, 2010 DSTS meeting, Copenhagen 30