POWER AND EFFECT SIZE POWER AND EFFECT SIZE

POWER AND EFFECT SIZE

POWER AND EFFECT SIZE Focusing on statistical significance and probability values can mislead: 1. Chance sampling variations suggest a worthless treatment really worked - the importance of minor findings are inflated if they hit the ‘magic’ alpha 5% threshold. 2. Important information may be overlooked in studies that just fall short of statistical significance, i. e. dismissed if 4. 9%. 3. Dividing research findings into two categories - significant and not significant with a rigid cut-off is gross oversimplification, since probability is a continuous scale.

ARE MY FINDINGS OF ANY REAL SUBSTANCE? • A statistically significant result can have little significance in the everyday sense • Statistical significance means no more than you can be confident that your results are unlikely to be a random variation in samples (sampling error) and reflect real differences and relationships.

EFFECT SIZE • Determines the strength of the relationship between the independent and dependent variables. • Reflect how large the effect of an independent variable was on the dependent variable.

MEASURES FOR ESTIMATING EFFECT SIZE 1. the standardized mean difference (d) 2. correlation coefficients such as r and phi 3. eta 2. This is a type of correlation known as the correlation ratio - used for determining the strength of association when there is a curvilinear rather than a linear relationship. For nonlinear relationships in which the correlation is not equal to zero, eta squared fits the points by a curved line.

Standardized mean difference for two groups • d: a ratio that measures the difference between the means for the levels of the independent variable relative to the within-group standard deviation. • Independent t test: d = Mexperimental – Mcontrol pooled within group SD • Paired or related groups design test: d = Mean of the differences between occasion SD of the differences

COHEN’S EFFECT SIZE CONVENTIONS • A small effect size: d = 0. 2 - an overlap of about 85% (the difference in height between 15 - and 16 -year-old girls). • A medium effect size: d = 0. 5 – an overlap of about 67% (the difference in height between 14 and 18 year-old girls). • A large effect size d = 0. 8 – an overlap only about 53% (the difference in height between 13 - and 18 -year-old girls).

CORRELATION COEFFICIENT METHOD: R AS AN EFFECT SIZE • Pearson product-moment correlation coefficient for two groups (r) is an effect size in itself (Chapter 15) • For a t test: r= t 2 + df • For the 2 x 2 chi square: rphi = chi square N • Larger chi square: contingency coefficient = chi square (chi square + N)

Eta 2 • An effect size for ANOVA (Chapter 13) • eta 2 = (between groups df )(F ratio) + within groups df • SPSS provides this eta 2 statistic in the printout

IMPORTANCE OF EFFECT SIZE • • • effect size can be used to summarize and compare a series of experiments that have included the same IV’s and DV’s. effect size provides information about the amount of impact an IV has had. It can be used to calculate the sample size needed for a study with a particular level of power.

POWER OF A STATISTICAL TEST • ability to detect differences • the probability of making a correct rejection of the null hypothesis when it is false • power depends both on the size of the treatment effect and sample size. In any study, the bigger the difference we obtain between the means of the two p u l a t i o n s , t h e m o r e p o w e r i n t h e s t u d y.

FACTORS THAT INFLUENCE POWER • • • Effect Size Increasing Sample Size Increasing the predicted difference between population means. Decreasing the population standard deviation. Using a less stringent level of significance. Using a one-tailed test.

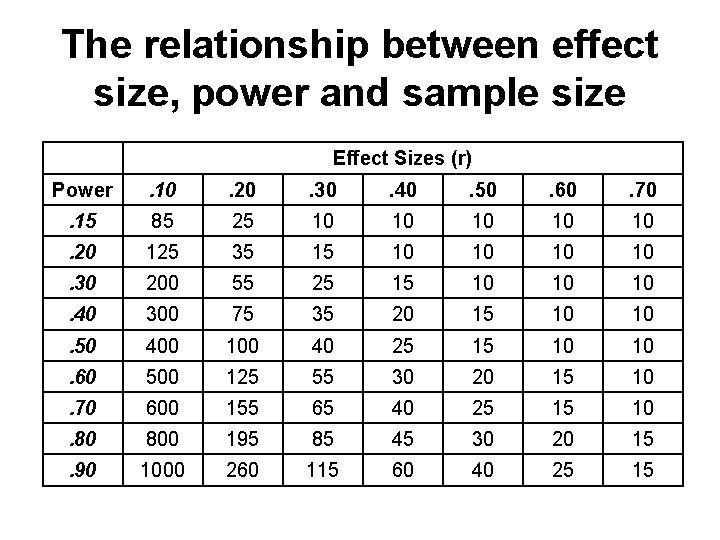
The relationship between effect size, power and sample size Effect Sizes (r) Power . 10 . 20 . 30 . 40 . 50 . 60 . 70 . 15 85 25 10 10 10 . 20 125 35 15 10 10 . 30 200 55 25 15 10 10 10 . 40 300 75 35 20 15 10 10 . 50 400 100 40 25 15 10 10 . 60 500 125 55 30 20 15 10 . 70 600 155 65 40 25 15 10 . 80 800 195 85 45 30 20 15 . 90 1000 260 115 60 40 25 15