Powells method Overview n Minimizing a function of

Powell’s method 박성진

Overview n Minimizing a function of multiple variables n n n Proceeding from starting point in some vector direction n -> minimizing f(p) along the line n by one-dimensional methods Critical part : Choosing the next direction n Not computing the function’s gradient

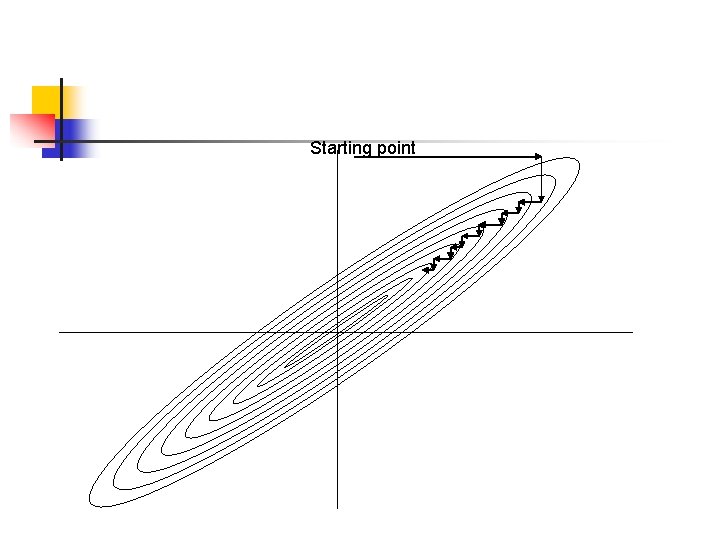
Simple method n n n Taking the unit vectors as a set of directions Moving along the first direction to its minimum, then from there along the second direction to its minimum Stop criteria : stop decreasing of function value Problem : in case of long, narrow valley at some angle to the coordinate basis vectors, requiring a series of many tiny steps Solution : needing a better set of directions than the unit vectors

Starting point

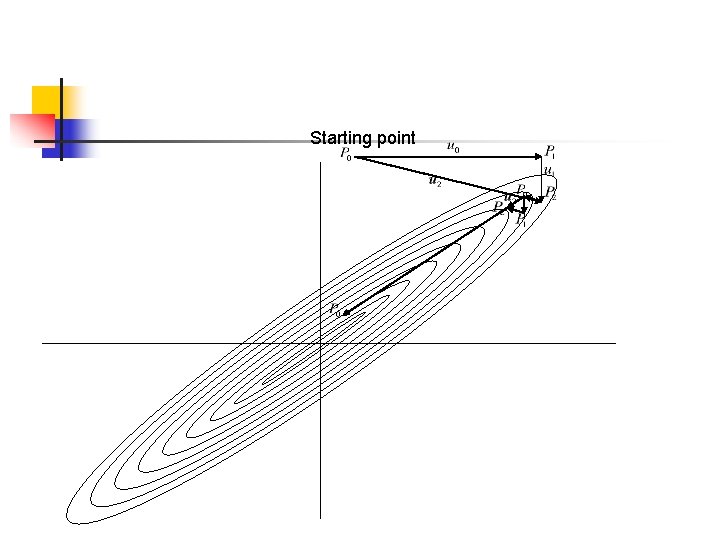
Powell’s quadratically convergent method n n n Save starting point as For i=1, …, N, move to the minimum along direction and call this point For i=1, …, N-1, set Set Move to the minimum along direction and call this point

Starting point

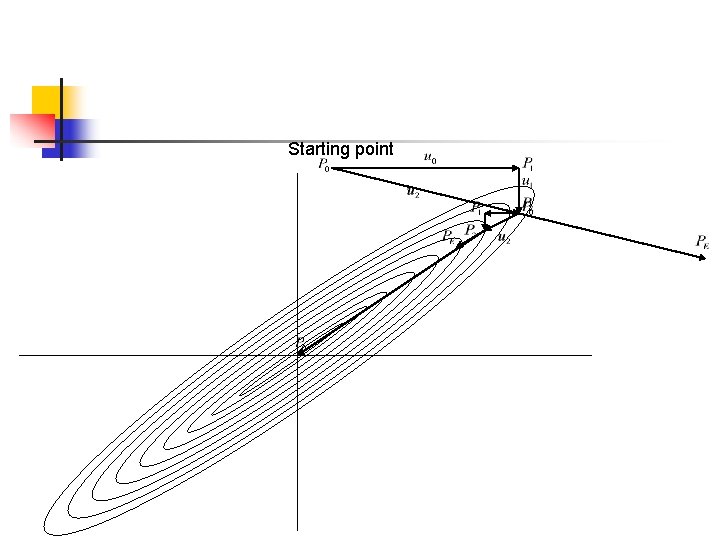
Powell’s quadratically convergent method n n Problem : at each stage, throwing in favor of -> becoming linearly dependent solution : n n n Reinitializing the set of directions to the basis vectors after every iterations Resetting the direction set to calculated principle directions of the matrix A Giving up the property of quadratic convergence -> finding a few good directions along narrow valleys

Modified Powell’s method n Keeping the old set of directions in two cases n n Assume : If n n The average direction is played out If n n Not primary direction due to any single direction’s decrease large substantial second derivative

Starting point

Code void powell(float p[], float **xi, int n, float ftol, int *iter, float *fret, float (*func)(float [])) { void linmin(float p[], float xi[], int n, float *fret, float (*func)(float [])); int i, ibig, j; float del, fptt, t, *ptt, *xit; pt=vector(1, n); ptt=vector(1, n); xit=vector(1, n); *fret=(*func)(p); for (j=1; j<=n; j++) pt[j]=p[j]; Save the initial point. for (*iter=1; ; ++(*iter)) { fp=(*fret); ibig=0; // ibig : 가장 큰 감소를 이룬 direction의 인덱 스 del=0. 0; for (i=1; i<=n; i++) { for (j=1; j<=n; j++) xit[j]=xi[j][i]; fptt=(*fret); linmin(p, xit, n, fret, func); // minimize along it, if (fptt-(*fret) > del) { del=fptt-(*fret); so far. ibig=i; } } if (2. 0*(fp-(*fret)) <= ftol*(fabs(fp)+fabs(*fret))+TINY) { free_vector(xit, 1, n); Termination criterion. free_vector(ptt, 1, n); free_vector(pt, 1, n); return; } if (*iter == ITMAX) nrerror("powell exceeding maximum iterations. "); for (j=1; j<=n; j++) { ptt[j]=2. 0*p[j]-pt[j]; xit[j]=p[j]-pt[j]; // xit : average direction pt[j]=p[j]; } fptt=(*func)(ptt); Function value at extrapolated point. if (fptt < fp) { t=2. 0*(fp-2. 0*(*fret)+fptt)*SQR(fp-(*fret)-del)del*SQR(fp-fptt); if (t < 0. 0) { linmin(p, xit, n, fret, func); for(j=1; j<=n; j++) { xi[j][ibig]=xi[j][n]; //가장 큰 감소를 이룬 direction제 거 xi[j][n]=xit[j]; } } }