Potential Energy of Multiple Charges Finding the Electric

-Potential Energy of Multiple Charges -Finding the Electric Field from the Electric Potential AP Physics C Mrs. Coyle

The Potential Energy of Point Charges n Consider two point charges, q 1 and q 2, separated by a distance r. The electric potential energy is n n This is the energy of the system, not the energy of just q 1 or q 2. Note that the potential energy of two charged particles approaches zero as r

Assume the sphere is a point charge. Apply conservation of energy. Ki + U i = K f + U f Ans: 1. 86 x 107 m/s

Potential Energy, U, of Multiple Charges n n If the two charges are the same sign, U is positive and work must be done to bring the charges together If the two charges have opposite signs, U is negative and work is done to keep the charges apart

U with Multiple Charges, final n n If there are more than two charges, then find U for each pair of charges and add them For three charges: q The result is independent of the order of the charges

Finding E From V n Assume, to start, that E has only an x component n Similar statements would apply to the y and z components Equipotential surfaces must always be perpendicular to the electric field lines passing through them n

E and V for an Infinite Sheet of Charge n n n The equipotential lines are the dashed blue lines The electric field lines are the brown lines The equipotential lines are everywhere perpendicular to the field lines

E and V for a Point Charge n n n The equipotential lines are the dashed blue lines The electric field lines are the brown lines The equipotential lines are everywhere perpendicular to the field lines

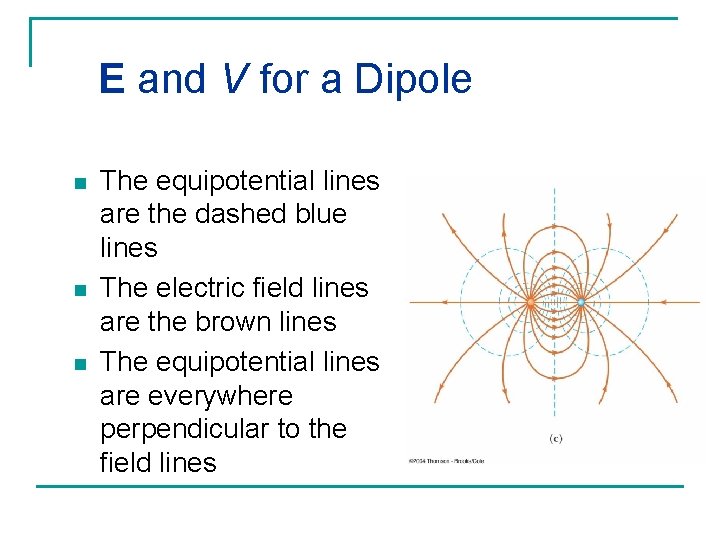
E and V for a Dipole n n n The equipotential lines are the dashed blue lines The electric field lines are the brown lines The equipotential lines are everywhere perpendicular to the field lines

Equipotential Lines Simulation of Field with Equipotential Lines http: //glencoe. mcgrawhill. com/sites/0078458137/student_view 0/chapter 21/elec tric_fields_applet. html

Electric Field from Potential, General n n In general, the electric potential is a function of all three dimensions Given V (x, y, z) you can find Ex, Ey and Ez as partial derivatives

Why are equipotentials always perpendicular to the electric field lines? n n When a test charge has a displacement, ds, along an equipotential surface d. V= 0 d. V= -E·ds=0 So E must be perpendicular to to the displacement along the equipotential surface. Note that no work is done to move a test charge along an equipotential surface.

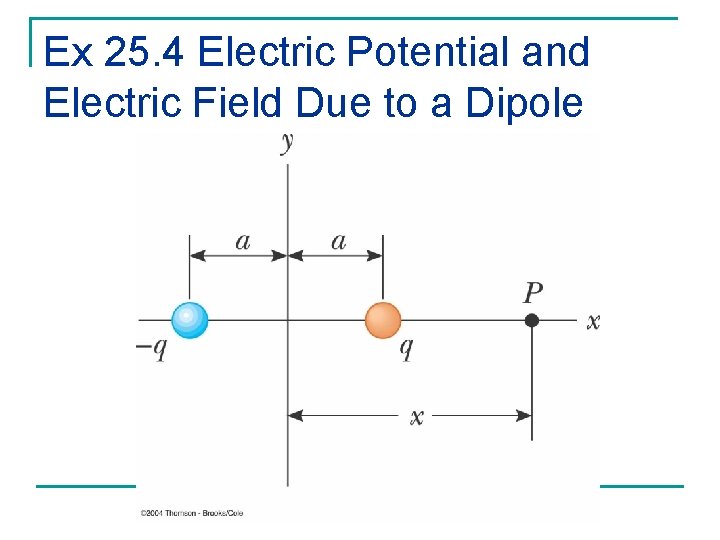
Ex 25. 4 Electric Potential and Electric Field Due to a Dipole

Ex 25. 4 Electric Potential and Electric Field Due to a Dipole n n An electric dipole consists of two charges of equal magnitude and opposite sign separated by a distance 2 a. The dipole is along the xaxis and is centered at the origin. a) Calculate the electric potential at P. b) Calculate V ans Ex at a point far from the dipole. c)Calculate V and Ex if point P is located anywhere between the two charges.

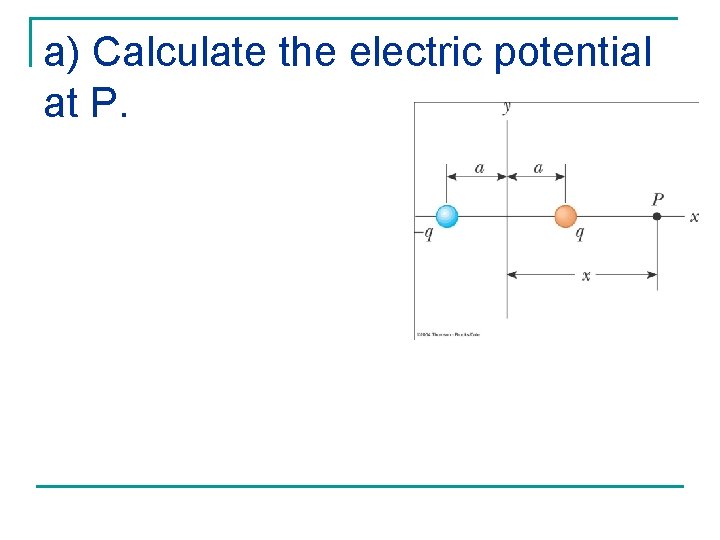
a) Calculate the electric potential at P.

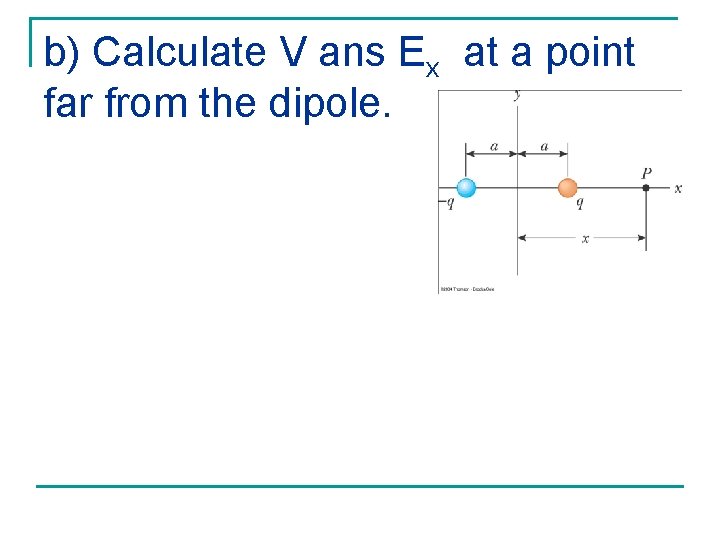
b) Calculate V ans Ex at a point far from the dipole.

c)Calculate V and Ex if point P is located anywhere between the two charges.

If point P is located to the left of the negative charge, what would be the potential?

Quick Quiz 25. 8 In a certain region of space, the electric potential is zero everywhere along the x axis. From this we can conclude that the x component of the electric field in this region is (a) zero (b) in the x direction (c) in the –x direction.

Quick Quiz 25. 8 Answer: (a). If the potential is constant (zero in this case), its derivative along this direction is zero.

Quick Quiz 25. 9 Answer: (b). If the electric field is zero, there is no change in the electric potential and it must be constant. This constant value could be zero but does not have to be zero.

Quick Quiz 25. 9 In a certain region of space, the electric field is zero. From this we can conclude that the electric potential in this region is (a) zero (b) constant (c) positive (d) negative