Potae a programovn 2 pro obor EST BPC

Počítače a programování 2 pro obor EST BPC 2 E PŘEDNÁŠKA 7 OSNOVA: a) Úvod do Matlabu b) Vektory a matice c) 2 D grafické výstupy Jiří Šebesta Ústav radioelektroniky, FEKT VUT v Brně

Úvod do Matlabu (1/5) • Co je to MATLAB – interaktivní programový systém The Math. Works, Inc. , který umožňuje na základě kombinace programovacích technik (odvozených od základních programovacích jazyků) a široké nabídky funkcí rychlé řešení rozsáhlých technických výpočtů, počítačového modelování a simulace – základním datovým typem MATLABu je matice (n – rozměr-né pole čísel), zkratka „MATrix LABoratory“ – jednotlivé výrazy, příkazy a volání funkcí lze provádět přímo v příkazovém okně nebo lze sekvenčně definovat v souboru s příponou m (***. m), který je možné sestavit v libovolném textovém editoru nebo editoru, který je součástí MATLABu – ve škole akademická licence (jen na PC v PC laboratoři) – bez spec. toolboxů lze použít GNU Octave (https: //www. gnu. org/software/octave/)

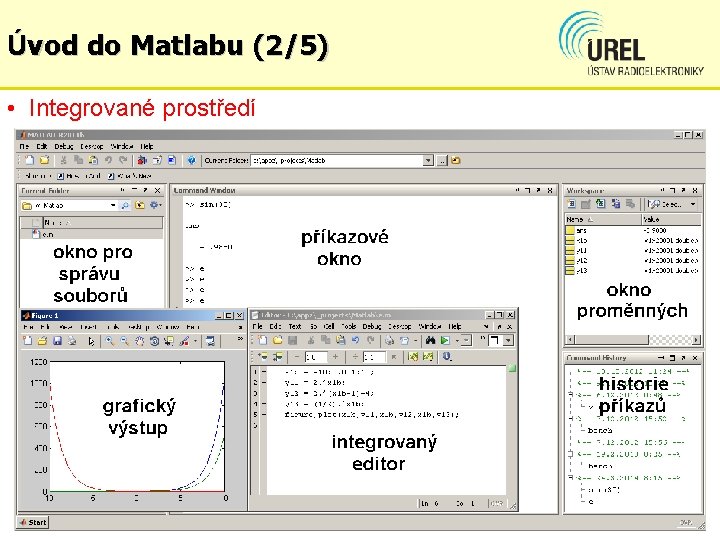
Úvod do Matlabu (2/5) • Integrované prostředí

Úvod do Matlabu (3/5) Příkazy v Matlabu ve tvaru: proměnná = výraz - Výrazy se skládají z operátorů, speciálních znaků, funkcí a proměnných. - Pokud chybí přiřazení proměnné, zavádí se systémová proměnná ans. - Umístěním středníku za výrazem potlačíme výstup na obrazovku. - Výsledkem je obecně matice, která se zobrazí na obrazovce. - Jména proměnných a funkcí musí začínat písmenem. - Rozlišují se malá a velká písmena ve jménech proměnných, funkcí a konstant. - Šipkami v příkazovém okně lze listovat v historii příkazů - Klávesou ESC se maže aktuální příkazový řádek

Úvod do Matlabu (4/5) • Příklad práce v příkazovém okně: >> 12458 / 45 ans = 276. 8444 >> b = 1 + 1 / 8; >> b = b + 1 >> b = 2. 1250 >> c = 1 + 8 i; >> d = 5. 5 - 3. 3 i; >> c + d ans = 6. 500 + 4. 700 i >> e = 2 e 2; >> f = 3 E-1; >> e + f ans = 200. 300 Zápis číselných konstant: 3. 14159 6. 6345 e 23 9. 12 E-20 5. 5 + 20. 1 i (komplexní číslo) Konstanty: pi i nebo j realmax realmin inf nan = 3. 141529…. imaginární jednotka maximální reálné číslo minimální reálné číslo nekonečno nedefinovaná hodnota

Úvod do Matlabu (5/5) Operátory v Matlabu: + sčítání == rovno - odečítání ~= nerovno * násobení < menší než / pravé dělení > větší než levé dělení <= menší nebo rovno ^ umocňování >= větší nebo rovno () definice priority >> u = 13*(2+3^3) u = 377. operace prvek po prvku (v matici) && podmínkový logický součin || podmínkový logický součet (podmínkový) & logický součet po prvcích (matice) | logický součet po prvcích (matice)

Vektory a matice (1/19) Generování vektoru Vektor v Matlabu se definuje výčtem prvků nebo definicí prvku vektoru na dané pozici, indexování je od 1. Pro generování vektoru s lineárně rostoucími (klesajícími) hodnotami lze použít notaci s dvojtečkou: vektor = od : <krok> : do Komentáře: >> u = [0 1 2 3 4]; % vycet prvku >> u(3) = 8; % definice jednoho prvku - na řádku za % u = 0 1 8 3 4 >> x = 1: 5 % notace s dvojteckou x = 1 2 3 4 5 >> y = 0: pi/4: pi y = 0. 0000 0. 7854 1. 5708 2. 3562 3. 1416 - celý blok %{ zakomentovaný blok %}

Vektory a matice (2/19) Transpozice vektoru: u = u' >> u = [0 1 2]’ % vycet prvku a transp. do sloup. vekt. u = 0 1 2 Přístup k položkám specifikací indexu (v kulatých závorkách): >> x = [0 1 2 8 14 23] >> x(4) ans = 8 Výběr části vektoru (od indexu: po index): >> x(3: 5) ans = 2 8 14

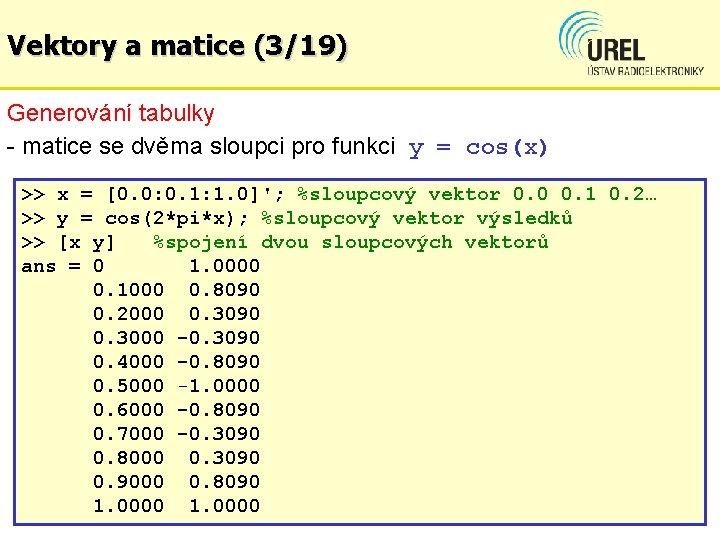
Vektory a matice (3/19) Generování tabulky - matice se dvěma sloupci pro funkci y = cos(x) >> x = [0. 0: 0. 1: 1. 0]'; %sloupcový vektor 0. 0 0. 1 0. 2… >> y = cos(2*pi*x); %sloupcový vektor výsledků >> [x y] %spojení dvou sloupcových vektorů ans = 0 1. 0000 0. 1000 0. 8090 0. 2000 0. 3090 0. 3000 -0. 3090 0. 4000 -0. 8090 0. 5000 -1. 0000 0. 6000 -0. 8090 0. 7000 -0. 3090 0. 8000 0. 3090 0. 9000 0. 8090 1. 0000

Vektory a matice (4/19) Generování matice Matice se v Matlabu definuje podobně jako vektor: výčtem prvků matice nebo definicí prvku matice na dané pozici. U dvourozměrné matice je první index řádkový, druhý je sloupcový. Středník odděluje řádky. >> A = [1 2 >> A(3, 1) = A = 1 3 0 >> B = [1: 5 B = 1 2 8 3; 3 4 5; 5 6 7]; % vycet prvku matice 3 x 3 0 % definice jednoho prvku 2 3 4 5 6 7 9; 2: 3: 17; 8 9 3: -1: 0] % notace s dvojteckou 2 3 4 5 9 5 8 11 14 17 9 3 2 1 0

Vektory a matice (5/19) Výběr řádků resp. sloupců Výběr řádku nebo sloupce z matice lze provést dvojtečkovou notací použitou pro definici prvků matice: Výběr m-tého řádku matice A: A(m, : ) Výběr n-tého sloupce matice A A(: , n) >> A = [1 2 3; 3 4 5; 5 6 7]; % vycet prvku matice 3 x 3 >> A(2, : ) ans = 3 % vektor z druhého řádku 4 5 >> A(: , 1) ans = 1 3 5 % vektor z prvního sloupce

Vektory a matice (6/19) Výběr části řádků resp. sloupců Výběr řádku nebo sloupce z matice lze provést dvojtečkovou notací s definicí od indexu: po index >> A = [11: 16; 21: 26; 31: 36; 41: 46] A = 11 12 13 14 15 16 21 22 23 24 25 26 31 32 33 34 35 36 41 42 43 44 45 46 >> A(2, 3: 5) % vektor z druhého řádku od sl. 3 po sl. 5 ans = 23 24 25 >> A(2: 4, 1: 4) ans = 21 31 41 % matice bez prvního řádku a posledních % dvou sloupců 22 23 24 32 33 34 42 43 44

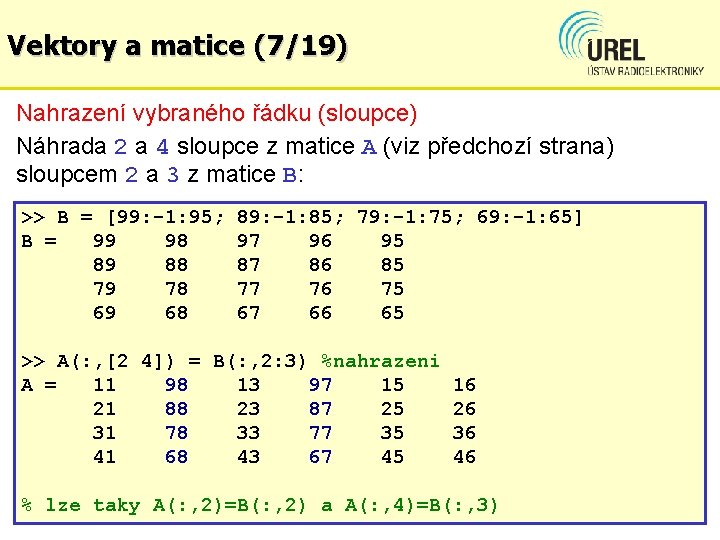
Vektory a matice (7/19) Nahrazení vybraného řádku (sloupce) Náhrada 2 a 4 sloupce z matice A (viz předchozí strana) sloupcem 2 a 3 z matice B: >> B = [99: -1: 95; B = 99 98 89 88 79 78 69 68 89: -1: 85; 79: -1: 75; 69: -1: 65] 97 96 95 87 86 85 77 76 75 67 66 65 >> A(: , [2 4]) = B(: , 2: 3) %nahrazeni A = 11 98 13 97 15 21 88 23 87 25 31 78 33 77 35 41 68 43 67 45 16 26 36 46 % lze taky A(: , 2)=B(: , 2) a A(: , 4)=B(: , 3)

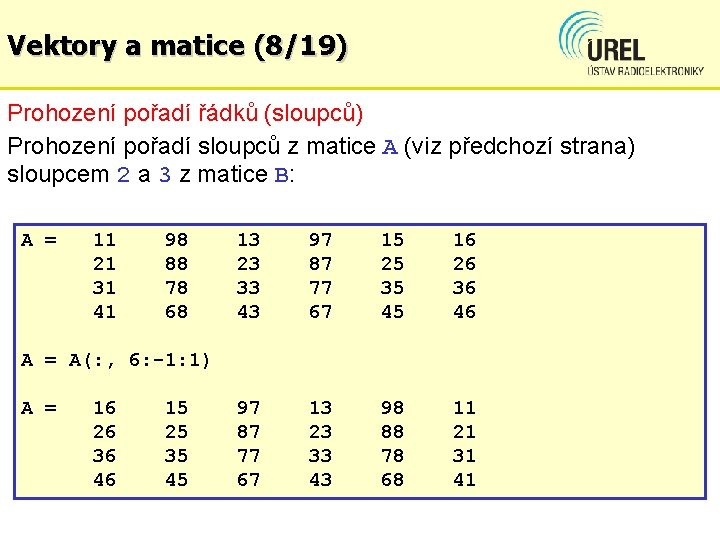
Vektory a matice (8/19) Prohození pořadí řádků (sloupců) Prohození pořadí sloupců z matice A (viz předchozí strana) sloupcem 2 a 3 z matice B: A = 11 21 31 41 98 88 78 68 13 23 33 43 97 87 77 67 15 25 35 45 16 26 36 46 97 87 77 67 13 23 33 43 98 88 78 68 11 21 31 41 A = A(: , 6: -1: 1) A = 16 26 36 46 15 25 35 45

Vektory a matice (9/19) Maticové operace – maticový součin (netečková notace) >> A = [1: 3; 4: 6; 7: 9] A = 1 2 3 4 5 6 7 8 9 >> B = [1 2 4; 2 3 4; 3 3 3] B = 1 2 4 2 3 4 3 3 3 >> A*B % maticový součin ans = 14 17 21 32 41 54 50 65 87 % pro prvek (1, 1): 1*1+2*2+3*3 = 1+4+9 = 14

Vektory a matice (10/19) Maticové operace – součin po prvcích (tečková notace) >> A = [1: 3; 4: 6; 7: 9] A = 1 2 3 4 5 6 7 8 9 >> B = [1 2 4; 2 3 4; 3 3 3] B = 1 2 4 2 3 4 3 3 3 >> A. *B % součin po prvcich – teckova notace ans = 1 4 12 8 15 24 21 24 27 % pro prvek (1, 1): 1*1 = 1

Vektory a matice (11/19) Podobně – skalární součin a součin po prvcích (tečková notace) >> X = [1 14 9 3] X = 1 14 9 3 >> Y = [2 8 -5 3] Y = 2 8 -5 3 >> X*Y’ %skalarni soucin = radkovy * sloupcovy (Y je %transponovany, vysledkem je jedno cislo - skalar ans = 78 %1*2 + 14*8 - 9*5 + 3*3 = 2 + 112 – 45 + 9 = 78 >> X. *Y %součin po prvcich – teckova notace – pozor %neni to vektorovy soucin ans = 2 112 -45 9 % pro prvek (1): 1*2 = 2

Vektory a matice (12/19) Pro vektorový součin dvou vektorů je v Matlabu připravena funkce cross() >> X = [4 5 6] X = 4 5 6 >> Y = [9 -5 4] Y = 9 -5 4 >> cross(X, Y) %vektorovy soucin, vysledkem je vektor %kolmy na vektory X a Y ans = 50 38 -65 %pro (1): X(2)*Y(3)- X(3)*Y(2) = %5*4 – 6*(-5) = 20 + 30 = 50

Vektory a matice (13/19) Transpozice matice – operátor ’ >> A = [1: 3; 4: 6; A = 1 2 4 5 7 8 >> B = A’ B = 1 4 2 5 3 6 7: 9] 3 6 9 7 8 9 Maticové dělení - pravé dělení Z = X/Y je řešením Z*Y = X - levé dělení Z = XY je řešením X*Z = Y

Vektory a matice (14/19) Příklad: Pravé maticové dělení: >> X = [1: 3; 4: 6; 7: 9] X = 1 2 3 4 5 6 7 8 9 >> Y = [2 2 3; 8 1 5; 3 -3 1] Y = 2 2 3 8 1 5 3 -3 1 >> Z = X/Y Z = 1. 4571 -0. 3143 0. 2000 1. 8000 0. 2000 -0. 4000 2. 1429 0. 7143 -1. 0000 >> Z*Y %kontrola Z*Y = X ans = 1. 0000 2. 0000 3. 0000 4. 0000 5. 0000 6. 0000 7. 0000 8. 0000 9. 0000

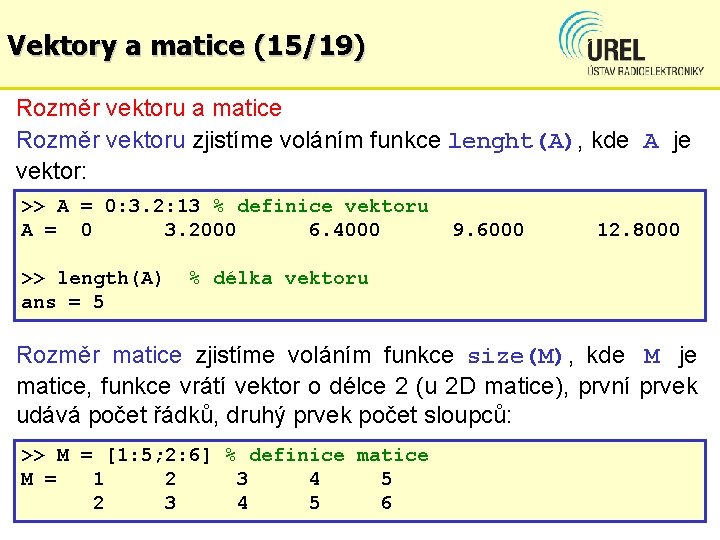
Vektory a matice (15/19) Rozměr vektoru a matice Rozměr vektoru zjistíme voláním funkce lenght(A), kde A je vektor: >> A = 0: 3. 2: 13 % definice vektoru A = 0 3. 2000 6. 4000 >> length(A) ans = 5 9. 6000 12. 8000 % délka vektoru Rozměr matice zjistíme voláním funkce size(M), kde M je matice, funkce vrátí vektor o délce 2 (u 2 D matice), první prvek udává počet řádků, druhý prvek počet sloupců: >> M = [1: 5; 2: 6] % definice matice M = 1 2 3 4 5 6

Vektory a matice (16/19) >> size(M) % rozměr matice ans = 2 5 %2 radky a 5 sloupcu Pokud chceme zjistit jen počet řádků: >> rows = size(M, 1) % počet radku rows = 2 %2 radky Pokud chceme zjistit jen počet sloupců: >> cols = size(M, 2) % počet sloupcu cols = 5 %5 sloupcu

Vektory a matice (17/19) Převod matice na vektor pomocí funkce reshape(M, 1, []), kde M je matice, druhý argument 1 definuje počet řádků po převodu a třetí argument počet sloupců, pokud je zadáno [], převede se na řádkový vektor celá matice (převádí se po sloupcích), v příkladu je uveden i převod na dvouřádkovou matici: >> M = [1: 4; 5: 8; 9: 12] %definice matice M = 1 2 3 4 5 6 7 8 9 10 11 12 >> V = reshape(M, 1, []) %jednoradkovy vektor V = 1 5 9 2 6 10 3 7 11 4 8 12 >> N = reshape(M, 2, []) %dvouradkova matice N = 1 9 6 3 11 8 5 2 10 7 4 12

Vektory a matice (18/19) Pokud potřebujeme převod na vektor po řádcích využijeme transpozici: >> M = [1: 4; 5: 8; 9: 12] %definice matice M = 1 2 3 4 5 6 7 8 9 10 11 12 >> V = reshape(M’, 1, []) %jednoradkovy vektor V = 1 2 3 4 5 6 7 8 9 10 11 12 >> N = reshape(M’, 2, []) %dvouradkova matice N = 1 2 3 4 5 6 7 8 9 10 11 12

Vektory a matice (19/19) Funkce sum() u vektoru sečte všechny prvky vektoru, výstupem je číslo, u matice se sečtou všechny prvky ve sloupci, výstupem je vektor s délkou rovnou počtu sloupů původní matice, pokud je třeba sčítat prvky v řádcích lze opět použít transpozici. >> V = 0: 2: 10 V = 0 2 4 6 8 10 >> sum(V) ans = 30 >> M = [1: 4; 5: 8; 9: 12] M = 1 2 3 4 5 6 7 8 9 10 11 12 >> sum(M) ans = 15 18 21 24

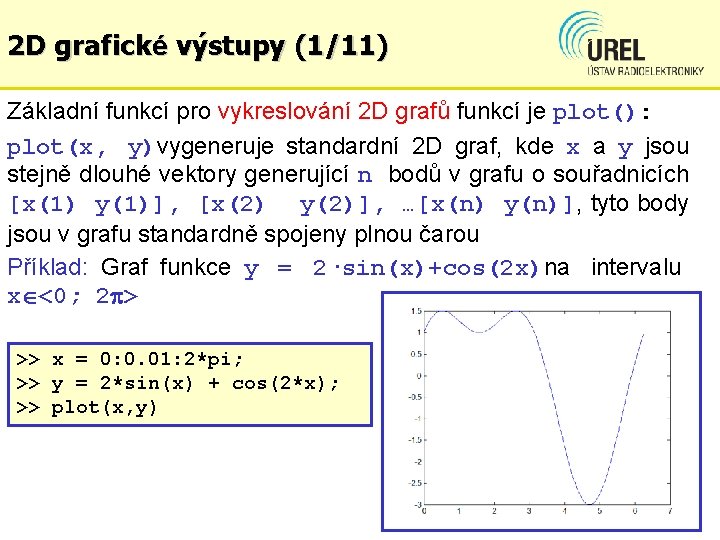
2 D grafické výstupy (1/11) Základní funkcí pro vykreslování 2 D grafů funkcí je plot(): plot(x, y)vygeneruje standardní 2 D graf, kde x a y jsou stejně dlouhé vektory generující n bodů v grafu o souřadnicích [x(1) y(1)], [x(2) y(2)], …[x(n) y(n)], tyto body jsou v grafu standardně spojeny plnou čarou Příklad: Graf funkce y = 2·sin(x)+cos(2 x)na intervalu x <0; 2 > >> x = 0: 0. 01: 2*pi; >> y = 2*sin(x) + cos(2*x); >> plot(x, y)

2 D grafické výstupy (2/11) plot(x, y, s)vygeneruje standardní 2 D graf (viz předchozí stránka, kde s je řetězec definující vizuální podobu vykreslované křivky. Řetězec s může obsahovat tyto specifické znaky: 1) barva čáry: b = modrá g = zelená r = červená c = tyrkysová m = fialová y = žlutá k = černá w = bílá 2) styl čáry: - = plná -- = čárkovaná : = tečkovaná -. = čerchovaná bez znaku = bez čar (jen body) 3) styl bodu: . = tečka * = hvězdička o = kroužek s = čtvereček + = křížek d = kosočtverec

2 D grafické výstupy (3/11) 3) styl bodu (pokrač. ): v = trojúhelník (vrchol dolů) < = trojúhelník (vrchol vlevo) p = pentagram ^ = trojúhelník (vrchol nahoru) > = trojúhelník (vrchol vpravo) h = hexagram Příklad: Model kružnice (parametrická definice): x = R·cos( ) y = R·sin( )na intervalu <0; 2 > po 0. 2 rad a pro R = 5 s vykreslením červenou tečkovanou čárou, body jako hvězdičky >> >> >> fi = 0: 0. 2: 2*pi; R = 5; x = R*cos(fi); y = R*sin(fi); plot(x, y, 'r: *')

2 D grafické výstupy (4/11) plot(x 1, y 1, s 1, x 2, y 2, s 2, … xn, yn, sn) vygeneruje více standardních 2 D grafů (viz předchozí stránky) do jednoho společného grafu Příklad: Kompozice dvou harmonických signálů s různou frekvencí a amplitudou (počáteční fáze je nulová) >> >> >> t = 0: 0. 001: 1; %casova osa f 1 = 4; % frekvence 1 f 2 = 2. 5; % frekvence 2 A 1 = 0. 5; %amplituda 1 A 2 = 0. 7; %amplituda 2 s 1 = A 1*sin(2*pi*f 1*t); s 2 = A 2*sin(2*pi*f 2*t); s = s 1 + s 2; plot(t, s 1, 'g', t, s 2, 'b', t, s, 'r')

2 D grafické výstupy (5/11) Další příkazy pro úpravu grafů: grid on a grid off - zobrazí resp. vypne mřížku hold on a hold off – do grafu se budou přidávat další křivky dalším voláním plot() resp. nové volání plot() překreslí celý graf (původní křivky se neobnoví) title('řetězec') – vloží do grafu titulek 'řetězec' xlabel('řetězec') – vloží do grafu popis x-ové osy s textem 'řetězec' ylabel('řetězec') – vloží do grafu popis y-ové osy s textem 'řetězec'

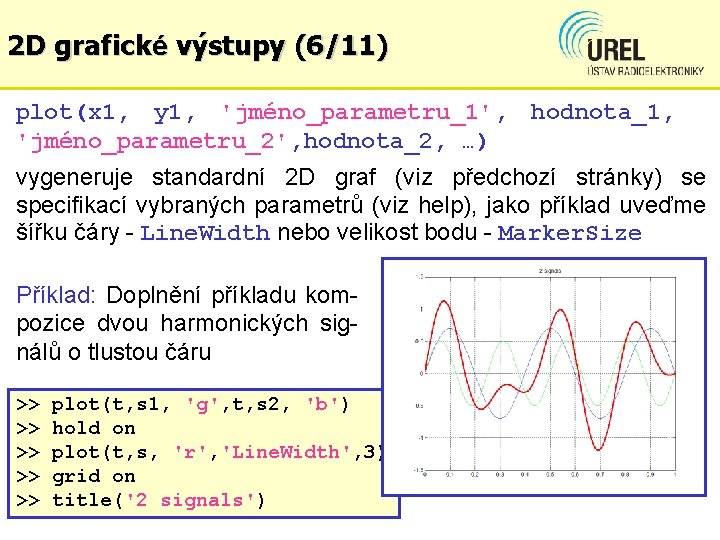
2 D grafické výstupy (6/11) plot(x 1, y 1, 'jméno_parametru_1', hodnota_1, 'jméno_parametru_2', hodnota_2, …) vygeneruje standardní 2 D graf (viz předchozí stránky) se specifikací vybraných parametrů (viz help), jako příklad uveďme šířku čáry - Line. Width nebo velikost bodu - Marker. Size Příklad: Doplnění příkladu kompozice dvou harmonických signálů o tlustou čáru >> >> >> plot(t, s 1, 'g', t, s 2, 'b') hold on plot(t, s, 'r', 'Line. Width', 3) grid on title('2 signals')

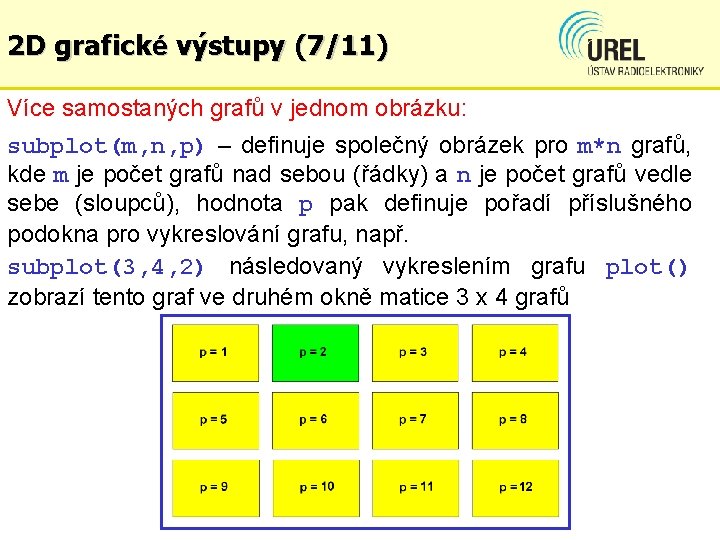
2 D grafické výstupy (7/11) Více samostaných grafů v jednom obrázku: subplot(m, n, p) – definuje společný obrázek pro m*n grafů, kde m je počet grafů nad sebou (řádky) a n je počet grafů vedle sebe (sloupců), hodnota p pak definuje pořadí příslušného podokna pro vykreslování grafu, např. subplot(3, 4, 2) následovaný vykreslením grafu plot() zobrazí tento graf ve druhém okně matice 3 x 4 grafů

2 D grafické výstupy (8/11) Příklad: Kompozice pěti harmonických signálů se základní harmonickou 50 Hz – parametry harmonických uloženy v matici S %{ Printing of six graphs into one figure using subplot function Graphs 1 to 5 display harmonic components generated from matrix S, where the 1 st column represents frequency in Hz, 2 nd amplitude in V, 3 rd initial phase in deg. Graph 6 display composition of all five harmonic component %} S = [50 100 150 200 250 3. 37 1. 23 0. 56 0. 13 0. 34 26. 4 33. 4 123. 0 22. 5 310. 5] t = 0: 0. 0001: 0. 02; %parameters %parameters %time vector of of of the the the 1 st 2 nd 3 rd 4 th 5 th harm. component component

2 D grafické výstupy (9/11) %1 st harmonic component sig 1 = S(1, 2)*sin(2*pi*S(1, 1)*t+S(1, 3)*pi/180); subplot(2, 3, 1) plot(t, sig 1, 'g') title('1 st harmonic') xlabel('t [s]') ylabel('u 1 [V]') grid on %2 nd harmonic component sig 2 = S(2, 2)*sin(2*pi*S(2, 1)*t+S(2, 3)*pi/180); subplot(2, 3, 2) plot(t, sig 2, 'g') title('2 nd harmonic') xlabel('t [s]') ylabel('u 2 [V]') grid on ……

2 D grafické výstupy (10/11) …… %5 th harmonic component sig 5 = S(5, 2)*sin(2*pi*S(5, 1)*t+S(5, 3)*pi/180); subplot(2, 3, 5) plot(t, sig 5, 'g') title('5 th harmonic') xlabel('t [s]') ylabel('u 5 [V]') grid on %signal composition sigc = sig 1+sig 2+sig 3+sig 4+sig 5; subplot(2, 3, 6) plot(t, sigc, 'r') title('signal composition') xlabel('t [s]') ylabel('u [V]') grid on

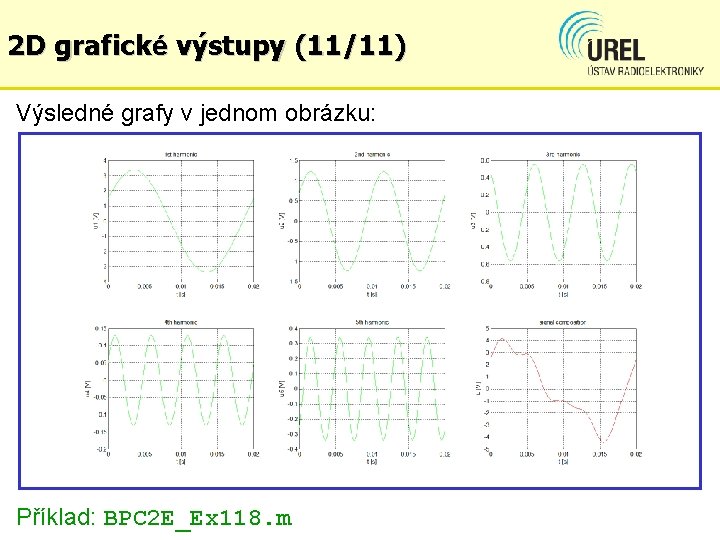
2 D grafické výstupy (11/11) Výsledné grafy v jednom obrázku: Příklad: BPC 2 E_Ex 118. m

DĚKUJI ZA POZORNOST Téma následující přednášky – Příkazy v Matlabu, standardní funkce, 3 D grafy