Postulates Postulate 1 A physical state is represented

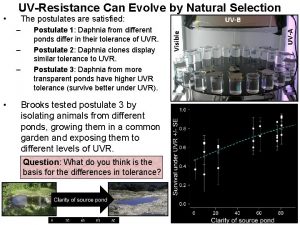
Postulates Postulate 1: A physical state is represented by a wavefunction The probablility to find the particle at within is . . Postulate 2: Physical quantities are represented by Hermitian operators acting on wavefunctions. Postulate 3: The evolution of a wavefunction is given by the Schrödinger equation. Postulate 4: The measurement of a quantity (operator A) can only give an eigenvalue an of A. Postulate 5: The probability to get an is measurement, the wavefunction collapes to eigenfunction). . After the (corresponding Postulate 6: N identical particles. The wavefunctions are either symmentrical (bosons) or antisymmetrical (fermions).

Orbital angular momentum + circ. perm. Commutation relations Eigenfunctions common to L 2, Lz Spherical harmonics integers Orthonormality Raising, lowering operators

One particle in a spherically symmetric potential H, L 2, Lz commute Eigenfunctions common to H, L 2, Lz Degeneracy Centrifugal potential Wavefunctions parity:

Angular momentum + circ. perm. Commutation relations Eigenfunctions common to J 2, Jz Integers or half-integers Addition of two angular momenta: Angular momentum Triangle rule L 2, Lz , S 2, Sz commute L 2, S 2, Jz commute Clebsch-Gordan coefficients

One particle in a spherically symmetric potential Eigenfunctions common to H, L 2, Lz , S 2, Sz L 2, S 2, Jz Eigenvalues Eigenfunctions common to H, Eigenvalues Also eigenfunctions to the spin-orbit interaction

Time-independent perturbation theory known ? Approximation ? Non-degenerate level Degenerate level (s times) First diagonalize H´ in the subspace corresponding to the degeneracy

Time-dependent perturbation theory known System in a at t=0 Probability to be in b at time t? Constant perturbation switched on at t=0 Continuum of final states with an energy distribution rb(E), width h Fermi’s Golden rule For

One particle in an electromagnetic field (I) Plane wave b a Absorption Line broadening Stimulated emission

One particle in an electromagnetic field (II) b Spectral intensity a Absorption Dipole approximation Selection rules Oscillator strength

One particle in a magnetic field Zeeman effect Paschen-Back effect Anomal Zeeman effect

One particle in an electric field Quadratic Stark effect (ground state) Linear Stark effect Tunnel ionisation

Many-electron atom Hc central field H 1 perturbation antisymmetrical/ permutation of two electrons Slater determinant Pauli principle Electon configuration, periodic system etc. . Wavefunctions common to Hc, L 2, Lz, S 2, Sz Beyond the central field approximation: LS coupling jj coupling 2 S+1 L terms