PostIGCSE Physics Course Experimental Physics using Data Loggers

Post-IGCSE Physics Course: Experimental Physics using Data Loggers and Computers 05 LCR Resonance (Waves & Electromagnetism) Dr Andrew French P 5/6 Winchester College Last updated April/May 2017

Experimental setup Sine wave voltage generator (688. 2 Hz currently) Windows PC running Pico. Scope software Picoscope USB oscilloscope A B Resistor (about 380 W) 1. 0 H inductor A – Voltage across signal generator B – Voltage across terminals of capacitor 0. 01 to 0. 1 m. F capacitor

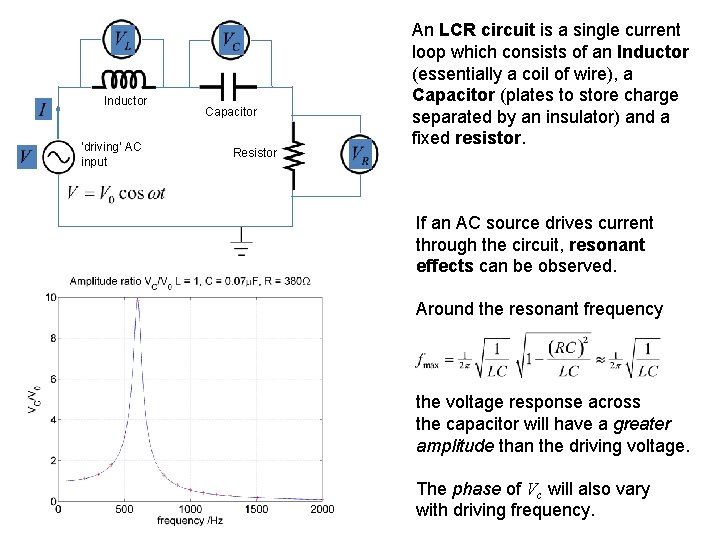
Inductor ‘driving’ AC input Capacitor Resistor An LCR circuit is a single current loop which consists of an Inductor (essentially a coil of wire), a Capacitor (plates to store charge separated by an insulator) and a fixed resistor. If an AC source drives current through the circuit, resonant effects can be observed. Around the resonant frequency the voltage response across the capacitor will have a greater amplitude than the driving voltage. The phase of Vc will also vary with driving frequency.

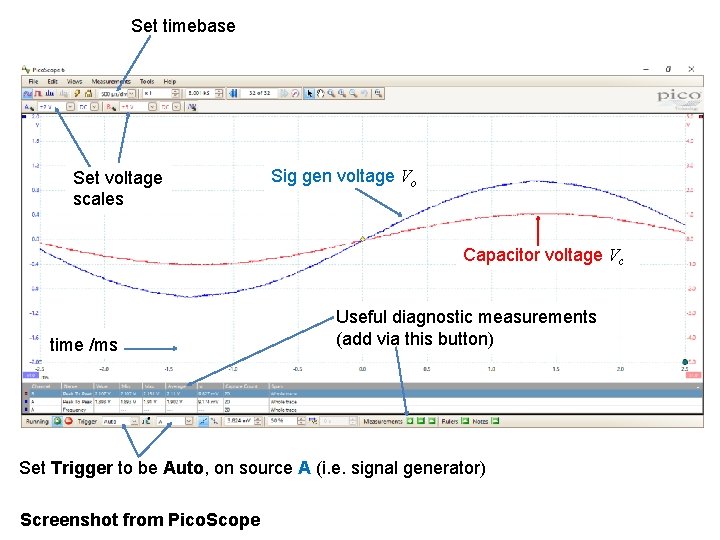
Set timebase Set voltage scales Sig gen voltage Vo Capacitor voltage Vc time /ms Useful diagnostic measurements (add via this button) Set Trigger to be Auto, on source A (i. e. signal generator) Screenshot from Pico. Scope

Experimental procedure Once Picoscope has been set up and both traces visible clearly, sweep the frequency over an appropriate range and then take screenshots (ctrl+alt+print screen) and paste into Irfan. View. Save a PNG bitmap image file with a filename which records the current frequency. e. g. 123 p 4 Hz. png means ‘ 100. 1 Hz’. A screenshot every 100 Hz might be a sensible first move for L = 1. 0 H and C = 0. 07 m. F, since . . Then more screenshots around the resonance peak might be a good idea (i. e. every 20 Hz instead of 100 Hz) The resonance frequency is fairly weakly dependent upon resistance, but the peak amplitude will change significantly with the value chosen. The goal of the experiment is to plot Vc amplitude and phase vs frequency for a variety of capacitances, so setting the resistor so that the resonance is ‘sharp enough to observe, but perhaps not too sharp to measure’ is the key idea. Turn the resistor knob and observe the effect near resonance. We need to measure resistance R to fit a model curve. Use a multimeter to achieve this.

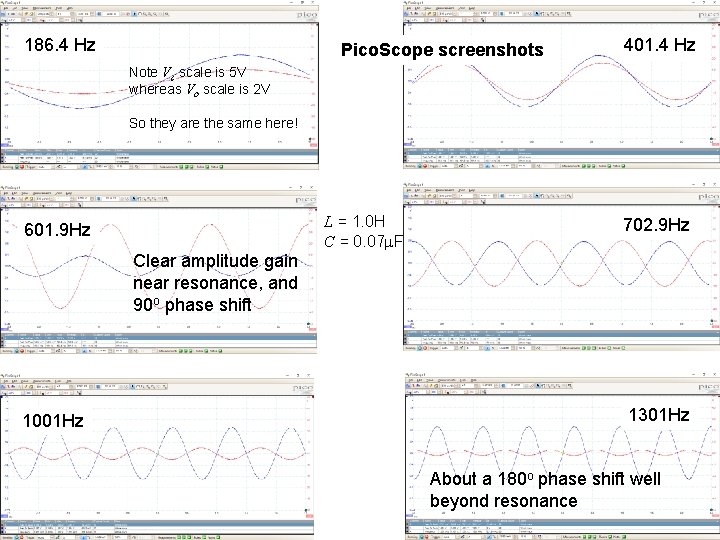
186. 4 Hz Pico. Scope screenshots 401. 4 Hz Note Vc scale is 5 V whereas Vo scale is 2 V So they are the same here! L = 1. 0 H C = 0. 07 m. F 601. 9 Hz 702. 9 Hz Clear amplitude gain near resonance, and 90 o phase shift 1001 Hz 1301 Hz About a 180 o phase shift well beyond resonance

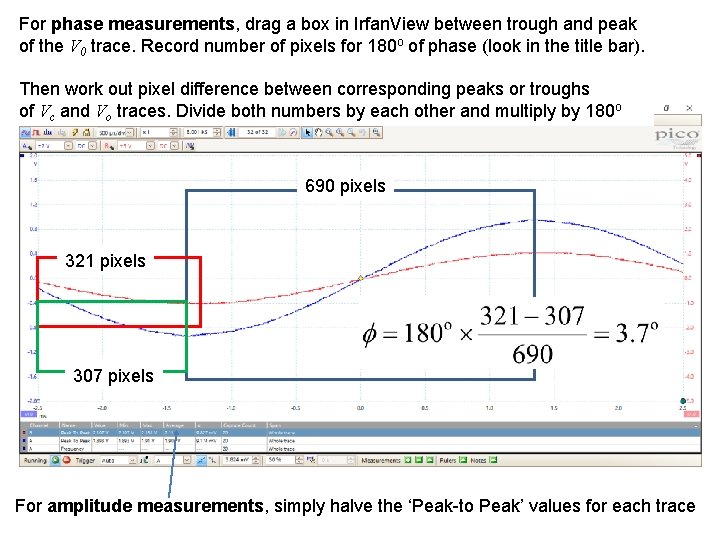
For phase measurements, drag a box in Irfan. View between trough and peak of the V 0 trace. Record number of pixels for 180 o of phase (look in the title bar). Then work out pixel difference between corresponding peaks or troughs of Vc and Vo traces. Divide both numbers by each other and multiply by 180 o 690 pixels 321 pixels 307 pixels For amplitude measurements, simply halve the ‘Peak-to Peak’ values for each trace

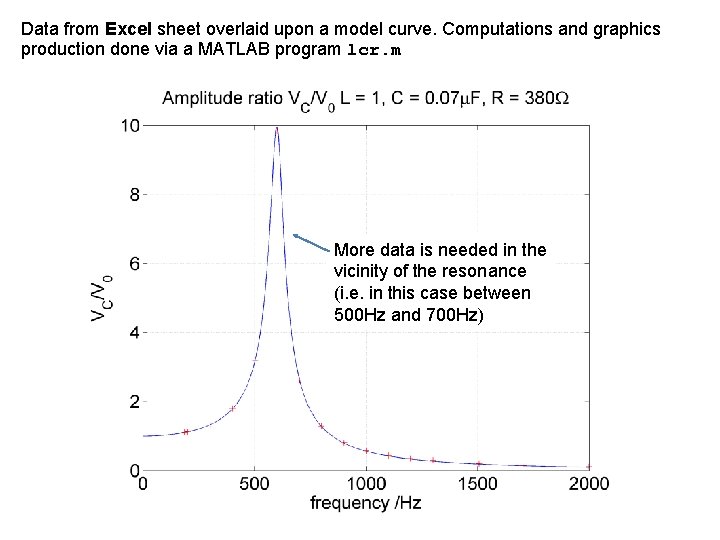
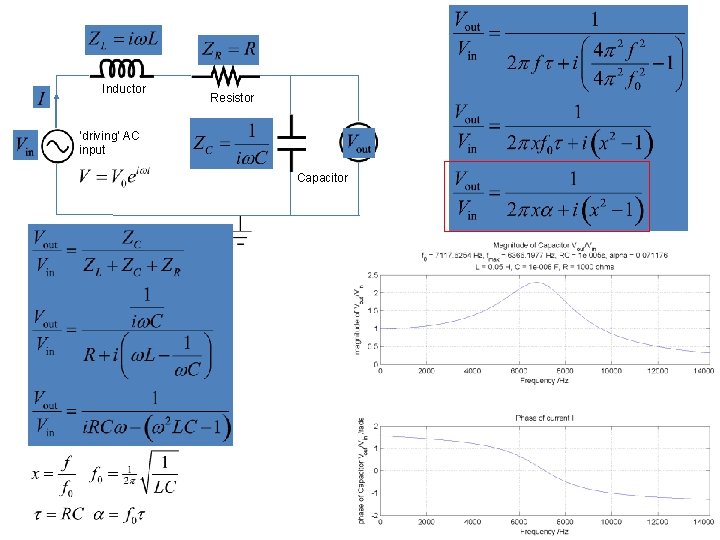
Data from Excel sheet overlaid upon a model curve. Computations and graphics production done via a MATLAB program lcr. m More data is needed in the vicinity of the resonance (i. e. in this case between 500 Hz and 700 Hz)

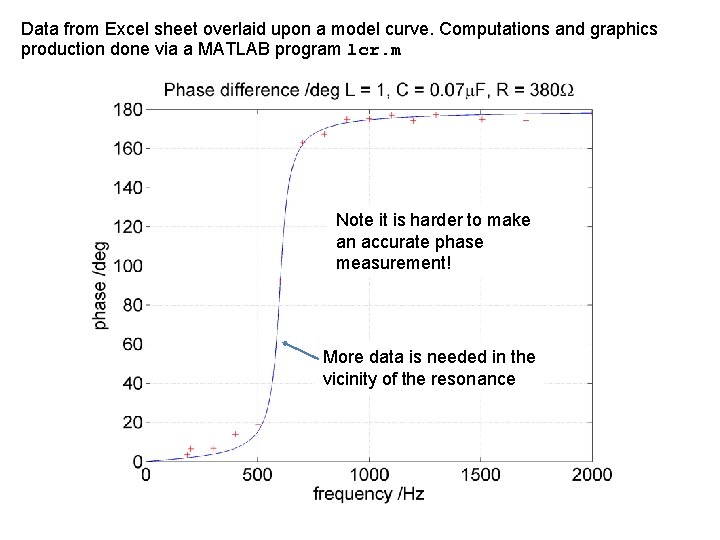
Data from Excel sheet overlaid upon a model curve. Computations and graphics production done via a MATLAB program lcr. m Note it is harder to make an accurate phase measurement! More data is needed in the vicinity of the resonance

MATLAB code lcr. m i. e. complex impedance potential divider idea

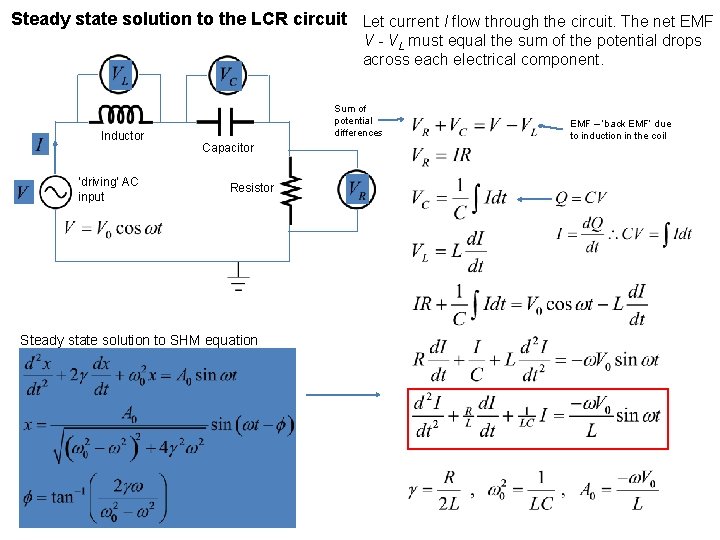
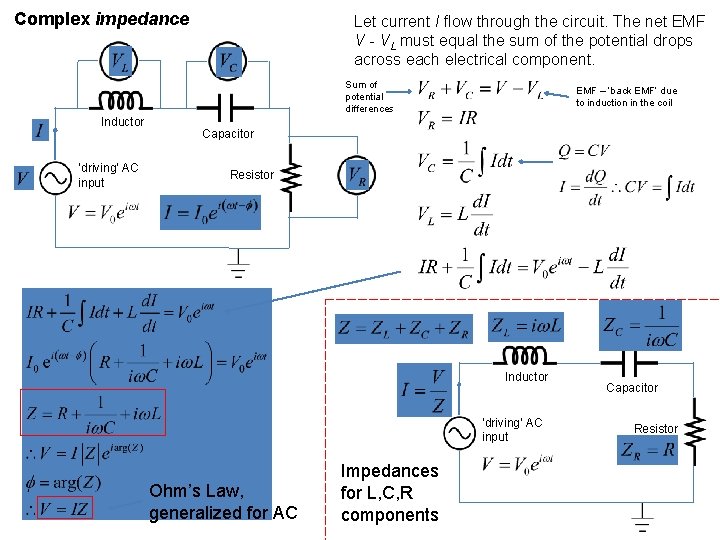
Steady state solution to the LCR circuit Let current I flow through the circuit. The net EMF V - VL must equal the sum of the potential drops across each electrical component. Inductor ‘driving’ AC input Sum of potential differences Capacitor Resistor Steady state solution to SHM equation EMF – ‘back EMF’ due to induction in the coil

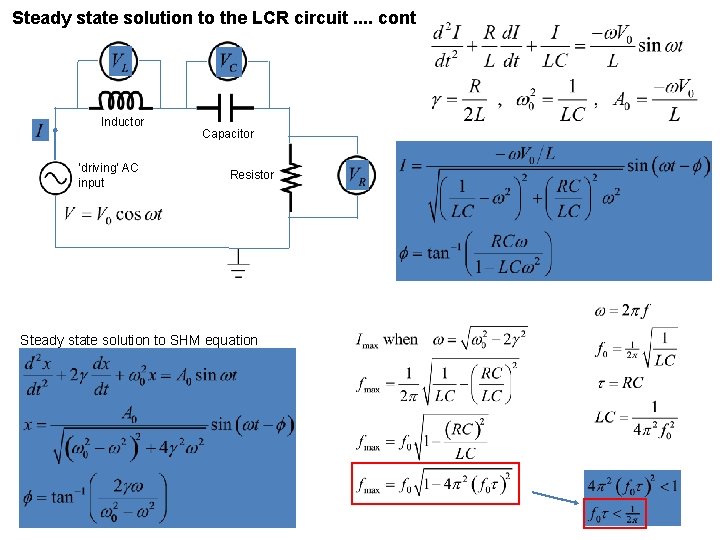
Steady state solution to the LCR circuit. . cont Inductor ‘driving’ AC input Capacitor Resistor Steady state solution to SHM equation

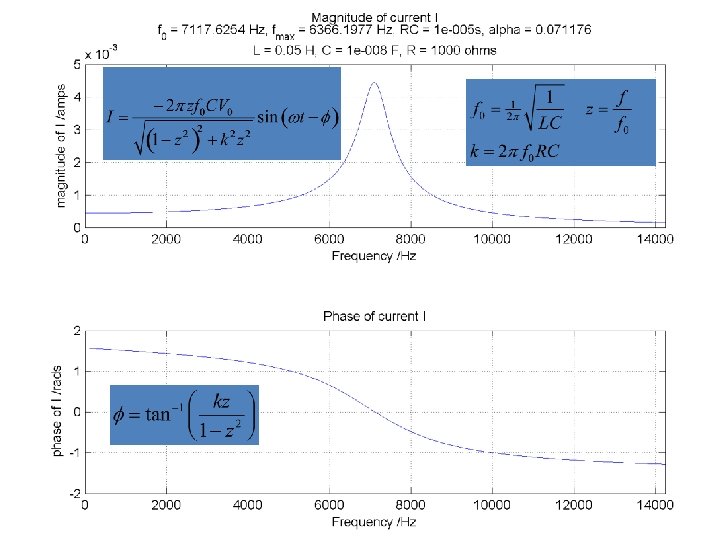
Using dimensionless variables. . . Note is the average current when the maximum amount of charge stored in the capacitor is discharged over one complete period at frequency f 0

Complex impedance Let current I flow through the circuit. The net EMF V - VL must equal the sum of the potential drops across each electrical component. Sum of potential differences Inductor ‘driving’ AC input EMF – ‘back EMF’ due to induction in the coil Capacitor Resistor Inductor ‘driving’ AC input Ohm’s Law, generalized for AC Impedances for L, C, R components Capacitor Resistor

Inductor Resistor ‘driving’ AC input Capacitor