Post hoc tests Ftest in ANOVA is the

Post hoc tests • F-test in ANOVA is the so-called omnibus test. It tests the means globally. It says nothing about which particular means are different. • post hoc tests, multiple comparison tests. • Tukey Honestly Significant Differences >Tukey. HSD(fit) #where fit comes from aov()

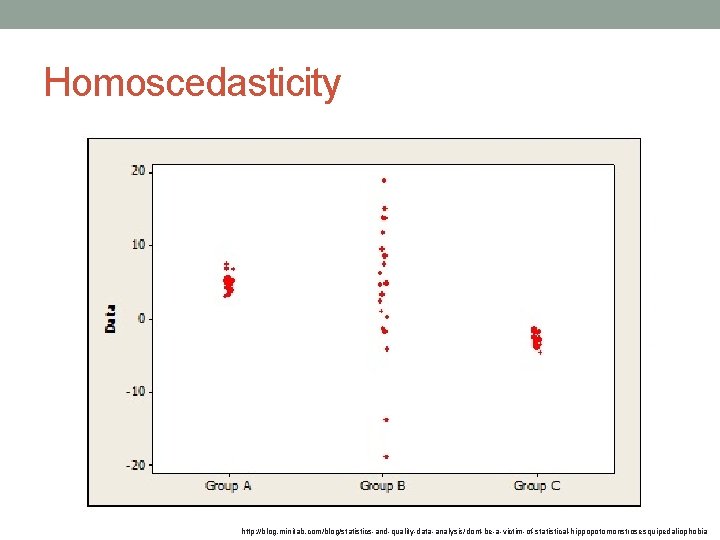
ANOVA assumptions • normality – all samples are from normal distribution • homogeneity of variance (homoscedasticity) – variances are equal • independence of observations – the results found in one sample won't affect others • Most influencial is the independence assumption. Otherwise, ANOVA is relatively robust. • We can sometimes violate • normality – large sample size • variance homogeneity – equal sample sizes + the ratio of any two variances does not exceed four

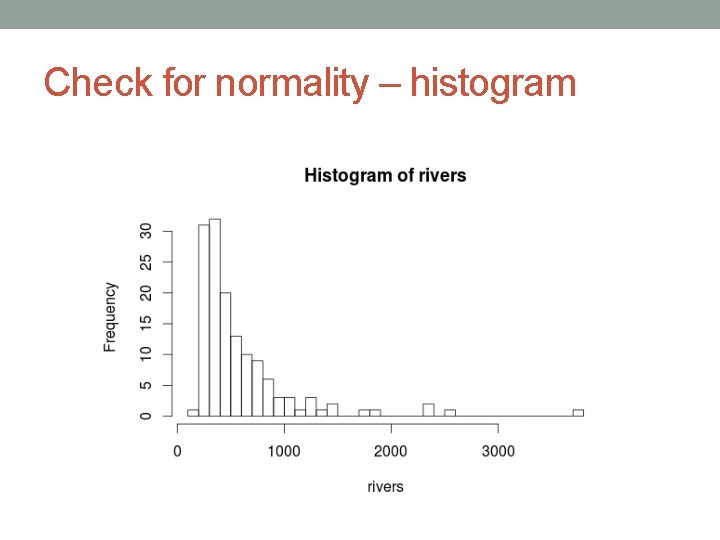
Check for normality – histogram

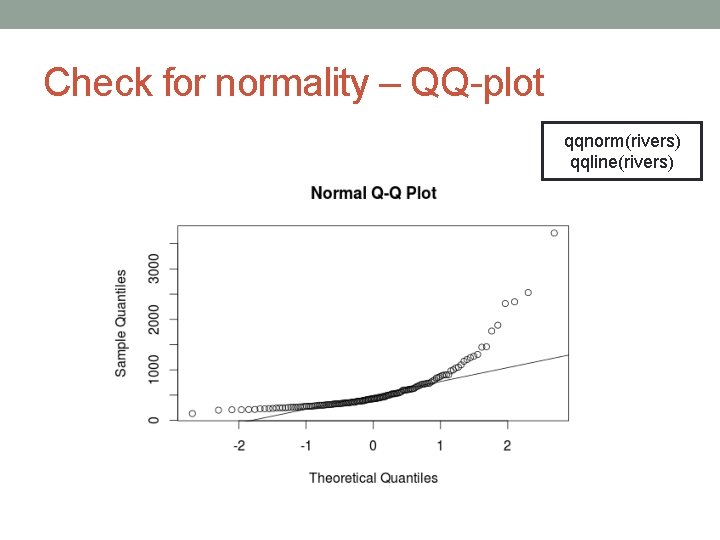
Check for normality – QQ-plot qqnorm(rivers) qqline(rivers)

Check for normality – tests • The graphical methods for checking data normality still leave much to your own interpretation. If you show any of these plots to ten different statisticians, you can get ten different answers. • H 0: Data follow a normal distribution. • Shapiro-Wilk test • shapiro. test(rivers): Shapiro-Wilk normality test data: rivers W = 0. 6666, p-value < 2. 2 e-16

Homoscedasticity http: //blog. minitab. com/blog/statistics-and-quality-data-analysis/dont-be-a-victim-of-statistical-hippopotomonstrosesquipedaliophobia

Tests for homoscedasticity •

Nonparametric statistics • Small samples from considerably non-normal distributions. • non-parametric tests • No assumption about the shape of the distribution. • No assumption about the parameters of the distribution (thus they are called non-parametric). • Simple to do, however their theory is extremely complicated. Of course, we won't cover it at all. • However, they are less accurate than their parametric counterparts. • So if your data fullfill the assumptions about normality, use paramatric tests (t-test, F-test).

Nonparametric tests • If the normality assumption of the t-test/ANOVA is violated, and the sample sizes are too small, then their nonparametric alternative should be used. • The nonparametric alternative of t-test is Wilcoxon test. > wilcox. test() • The nonparametric alternative of ANOVA is Kruskal- Wallis test > kruskal. test()

ANOVA kinds • one-way ANOVA (analýza rozptylu při jednoduchém třídění, jednofaktorová ANOVA) > aov(beer_brands$Price~beer_brands$Brand) dependent variable independent variable • two-way ANOVA (analýza rozptylu dvojného třídění, dvoufaktorová ANOVA) • Example: engagement ratio, measure two educational methods (with and without song) for men and women independently > aov(engagement~method+sex) • interactions between factors

CORRELATION

Introduction • Up to this point we've been working with only one variable. • Now we are going to focus at two variables. • Two variables that are probably related. Can you think of some examples? • weight and height • time spent studying and your grade • temperature outside and ankle injuries

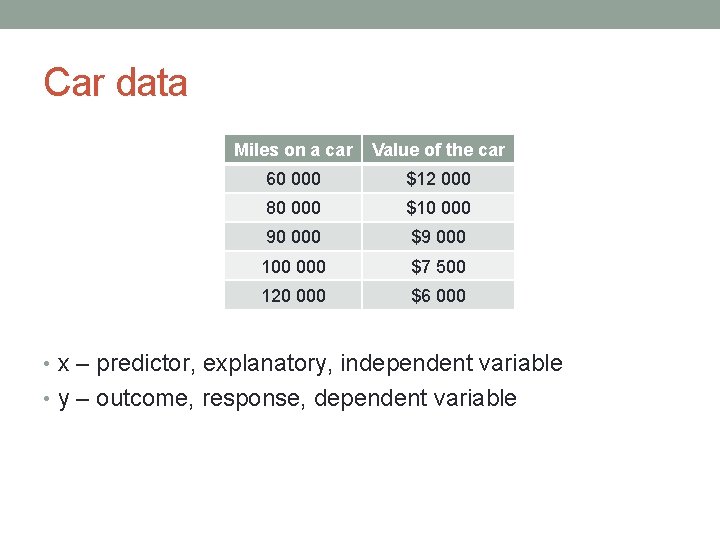
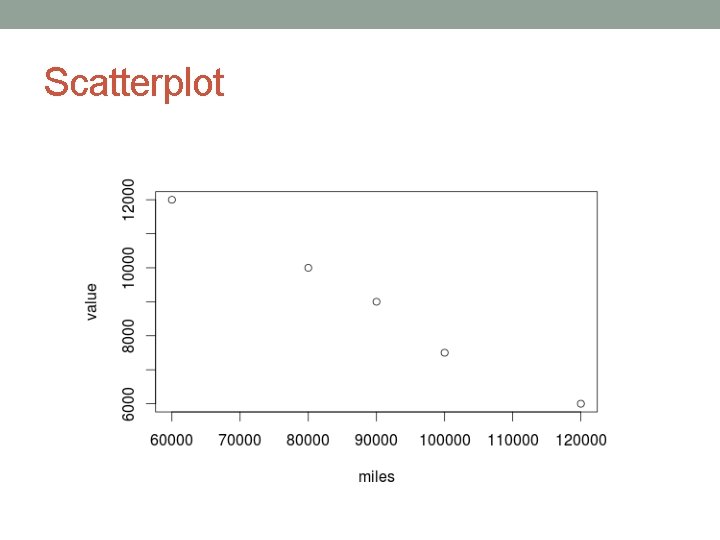
Car data Miles on a car Value of the car 60 000 $12 000 80 000 $10 000 90 000 $9 000 100 000 $7 500 120 000 $6 000 • x – predictor, explanatory, independent variable • y – outcome, response, dependent variable

Car data Miles on a car Value of the car 60 000 $12 000 80 000 $10 000 90 000 $9 000 100 000 $7 500 120 000 $6 000 • How may we show these variables have a relationship? • Tell me some of yours ideas. • scatterplot

Scatterplot

Stronger relationship?

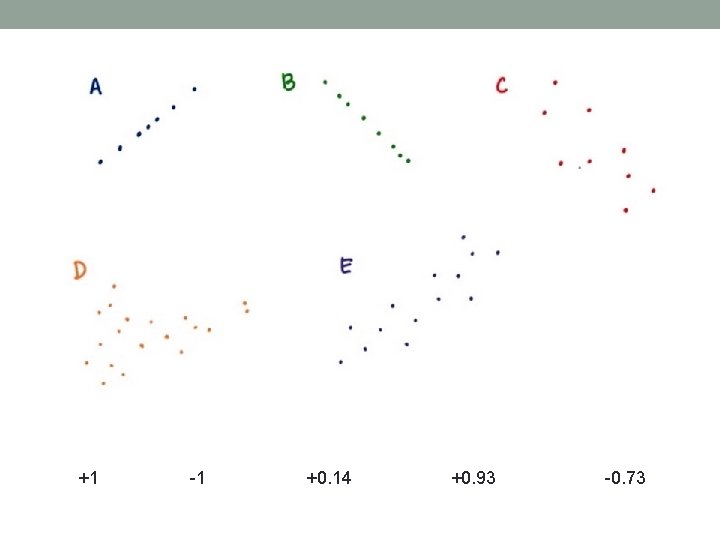
Correlation • Relation between two variables = correlation • strong relationship = strong correlation, high correlation Match these strong positive strong negative weak positive weak negative

Correlation coefficient •

+1 -1 +0. 14 +0. 93 -0. 73

Coefficient of determination • r 2 = 0. 25 r 2 = 0. 81 from http: //www. sagepub. com/upm-data/11894_Chapter_5. pdf

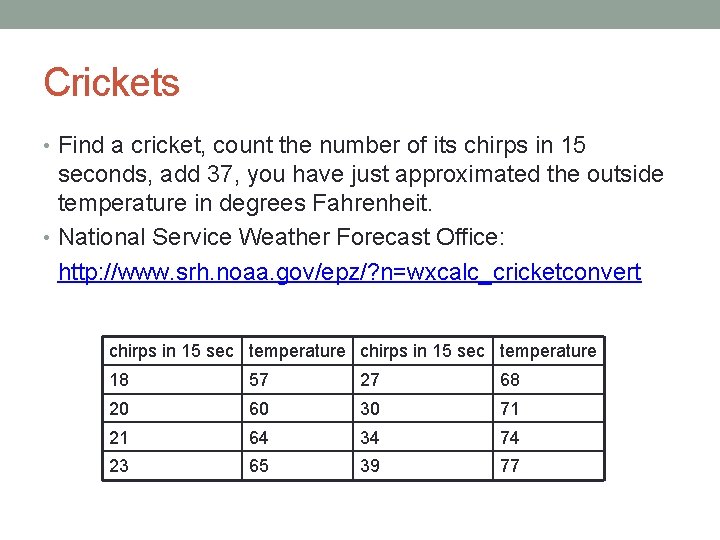
Crickets • Find a cricket, count the number of its chirps in 15 seconds, add 37, you have just approximated the outside temperature in degrees Fahrenheit. • National Service Weather Forecast Office: http: //www. srh. noaa. gov/epz/? n=wxcalc_cricketconvert chirps in 15 sec temperature 18 57 27 68 20 60 30 71 21 64 34 74 23 65 39 77

Hypothesis testing • A B C D

Hypothesis testing •

Correlation vs. causation • causation – one variable causes another to happen • For example, the fact that it is raining causes people to take their umbrellas. • correlation – just means there is a relationship • For example, do happy people have more friends? Are they just happy because they have more friends? Or they act a certain way which causes them to have more friends.

Correlation vs. causation • There is a strong relationship between the ice cream consumption and the crime rate. • How could this be true? • The two variables must have something in common with one another. It must be something that relates to both level of ice cream consumption and level of crime rate. Can you guess what that is? • Outside temperature. from causeweb. org

Correlation vs. causation • Outside temperature is a variable we did not realize to control. • Such variable is called third variable, confounding variable, lurking variable. • The methodologies of scientific studies therefore need to control for these factors to avoid a 'false positive‘ conclusion that the dependent variables are in a causal relationship with the independent variable.

Correlation vs. causation • If you stop selling ice cream, does the crime rate drop? What do you think? • That’s because correlation expresses the association between two or more variables; it has nothing to do with causality. • In other words, just because level of ice cream consumption and crime rate increase/descrease together does not mean that a change in one necessarily results in a change in the other. • You can’t interpret associations as being causal.

http: //xkcd. com/552/

Correlation and regression analysis • Correlation analysis investigates the relationships between variables using graphs or correlation coefficients. • Regression analysis answers the questions like: which relationship exists between variables X and Y (linear, quadratic , …. ), is it possible to predict Y using X, and with what error?

Simple linear regression •

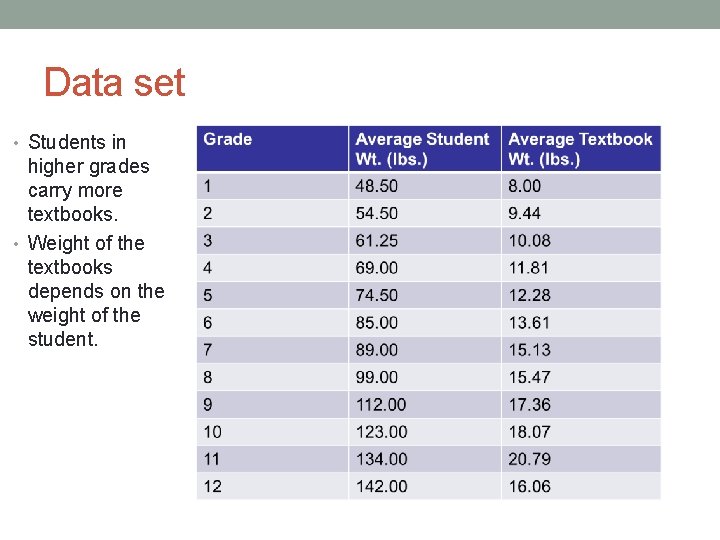
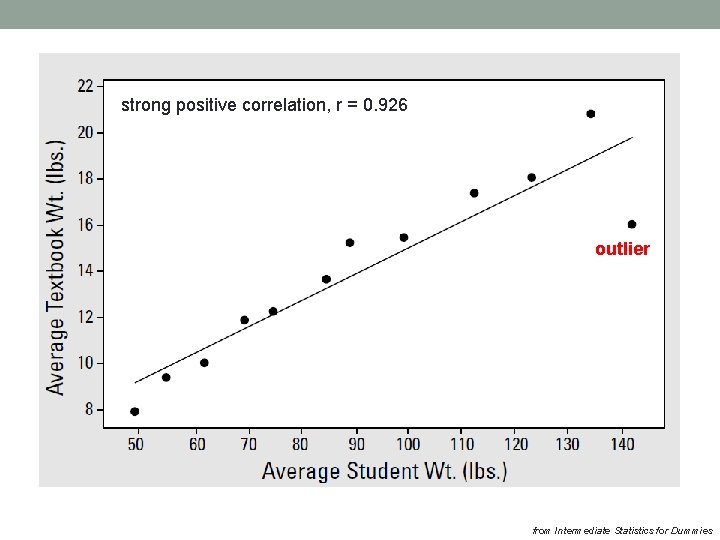
Data set • Students in higher grades carry more textbooks. • Weight of the textbooks depends on the weight of the student.

strong positive correlation, r = 0. 926 outlier from Intermediate Statistics for Dummies

Build a model • Find a straight line y = a + bx

Interpretation • y-intercept (3. 69 in our case) • it may or may not have a practical meaning • Does it fall within actual values in the data set? If yes, it is a clue it may have a practical meaning. • Does it fall within negative territory where negative y-value are not possible? (e. g. weights can’t be negative) • Does a value x = 0 have practical meaning (student weighting 0)? • However, even if it has no meaning, it may be necessary (i. e. significantly different from zero)! • slope • change in y due to one-unit increase in x (i. e. if student’s weight increases by 1 pound, its textbook’s weight increases by 0. 113 pounds) • now you can use regression line to estimate y value for new x

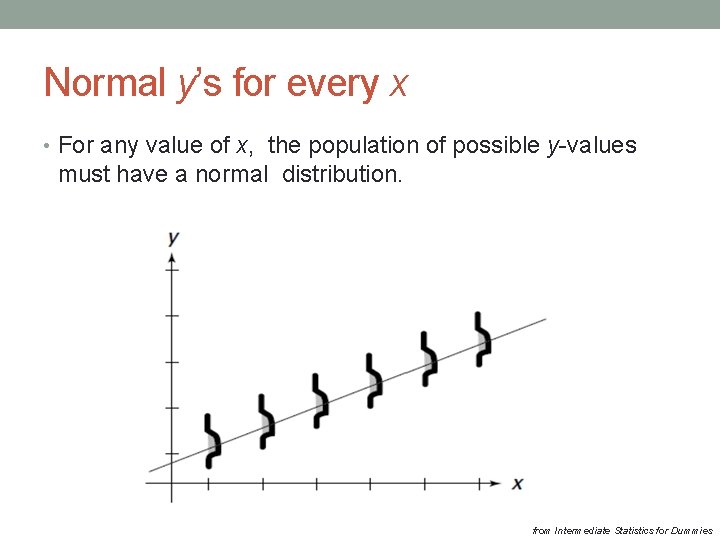
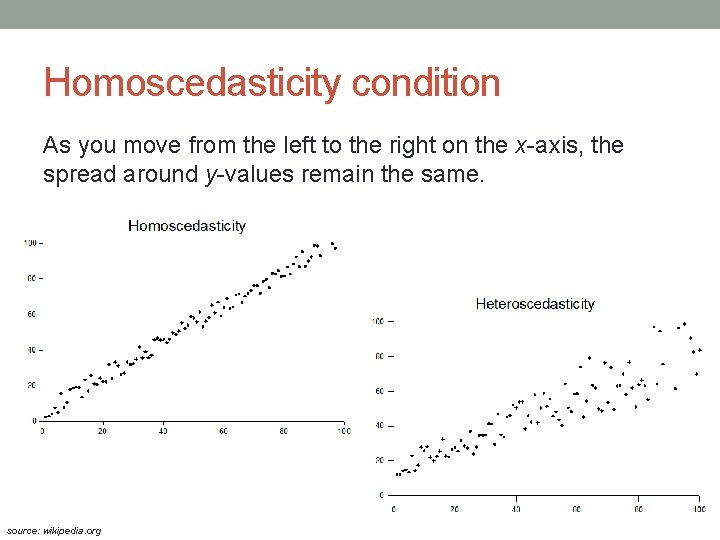
Regression model conditions • After building a regression mode you need to check if the required conditions are met. • What are these conditions? • The y’s have normal distribution for each value of x. • The y’s have constant spread (standard deviation) for each value of x.

Normal y’s for every x • For any value of x, the population of possible y-values must have a normal distribution. from Intermediate Statistics for Dummies

Homoscedasticity condition As you move from the left to the right on the x-axis, the spread around y-values remain the same. source: wikipedia. org

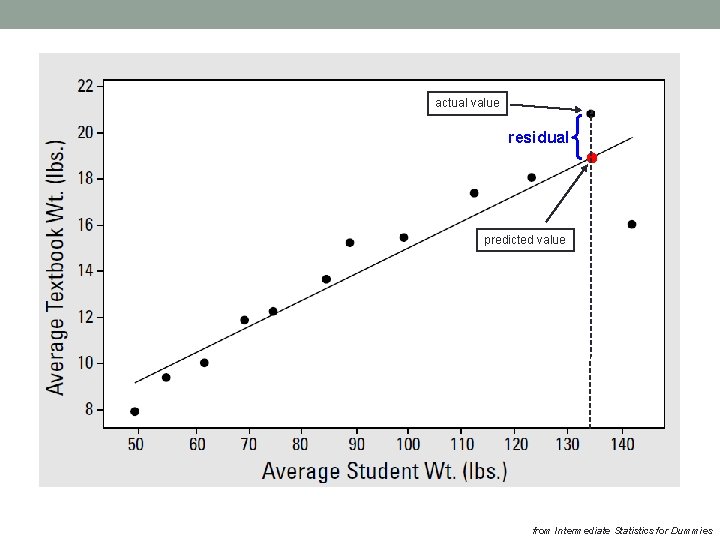
Residuals •

actual value residual predicted value from Intermediate Statistics for Dummies

Residuals • The residuals are data just like any other, so you can find their mean (which is zero!!) and their standard deviation. • Residuals can be standardized, i. e. converted to the Zscore so you see where they fall on the standard normal distribution. • Plotting residuals on the graph – residual plots.

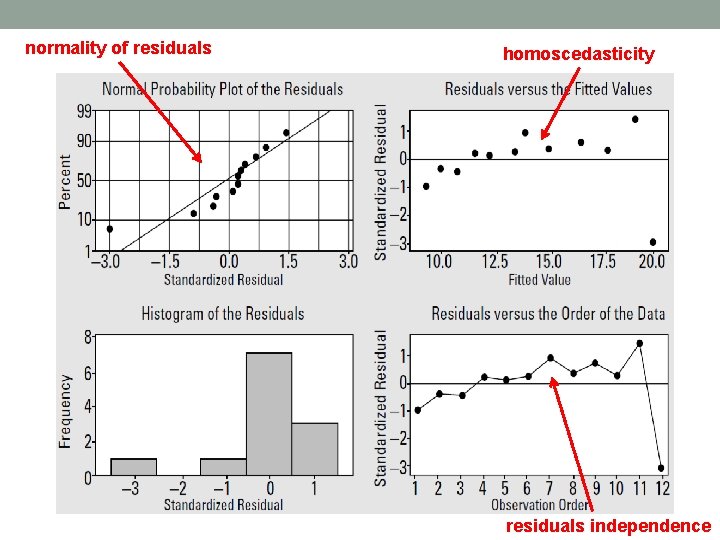
normality of residuals homoscedasticity residuals independence

Using r 2 to measure model fit • r 2 measures what percentage of the variability in y is explained by the model. • The y-values of the data you collect have a great deal of variability. • You look for another variable (x) that helps to explain the variability in the y-values. • After you put x into the model and you find it’s highly correlated with y, you want to find out how well this model did at explaining why the values of y are different.

Interpreting r 2 • high r 2 (80 -90% is extremely high, 70% is fairly high) • A high percentage of variability means that the line fits well because there is not much left to explain about the value of y other than using x and its relationship to y. • small r 2 (0 -30%) • The model containing x doesn’t help much in explaining the difference in the yvalues • The model would not fit well. You need another variable to explain y other than the one you already tried. • middle r 2 (30 -70%) • x does help somewhat in explaining y, but it doesn’t do the job well enough on its own. • Add one or more variables to the model to help explain y more fully as a group. • Textbook example: r = 0. 93, r 2 = 0. 8649. Approximately 86% of variability you find in textbook weights for is explained by the average student weight. Fairly good model.

Multiple regression • Two (or more) variables are better than one. • y = b 0 + b 1 x 1 + b 2 x 2 + … + bkxk • Steps in the analysis • Check the relationships between each x variable and y (using scatterplots and correlations) and use the results to eliminate those x variables that aren’t strongly related to y. • Look at possible relationships between the x variables themselves to make sure you aren’t being redundant (in statistical terms, you’re trying to avoid the problem of multicolinearity). If two x variables relate to y the same way, you don’t need both in the model. • Use selected x variables in a multiple regression analysis to find the best-fitting model for your data. • Use the best-fitting model to predict y for given x-values.

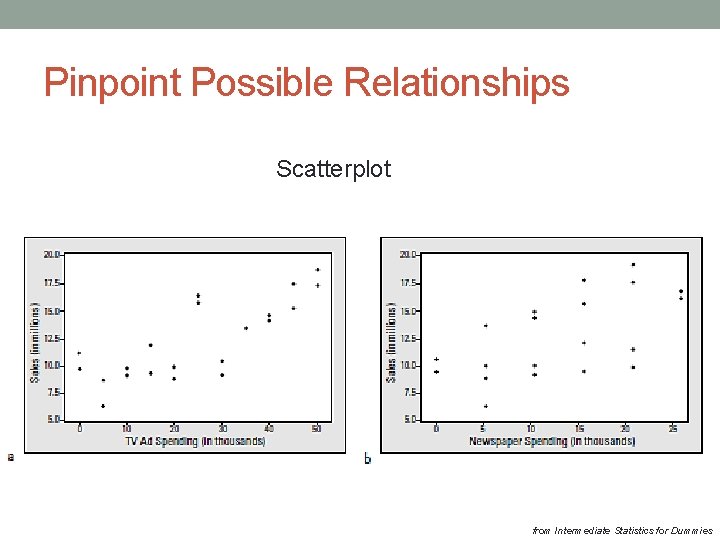
Data set Relate plasma TV sales with two types of advertisement. from Intermediate Statistics for Dummies

Pinpoint Possible Relationships Scatterplot from Intermediate Statistics for Dummies

Correlations • All possible correlations • TV vs. Sales • Newspaper vs. TV from Intermediate Statistics for Dummies

• Is correlation coefficient ρ statistically significant? • What is the null hypothesis? • Ho: ρ = 0, Ha: ρ ≠ 0 • Investigate p-values. • If p-value is smaller than α (typically 0. 05), reject Ho. from Intermediate Statistics for Dummies

Checking for Multicolinearity • Look at the relationship between the x variables themselves and check for redundancy. • Multicolinearity – two x variables are highly correlated. • If two x variables are significantly correlated, include only one. • If you include both, the computer won’t know what numbers to give as coefficients for each of the two variables, because they share their contribution to determining the value of y. • Multicolinearity can really mess up the model-fitting. from Intermediate Statistics for Dummies

Find the best fitting model from Intermediate Statistics for Dummies

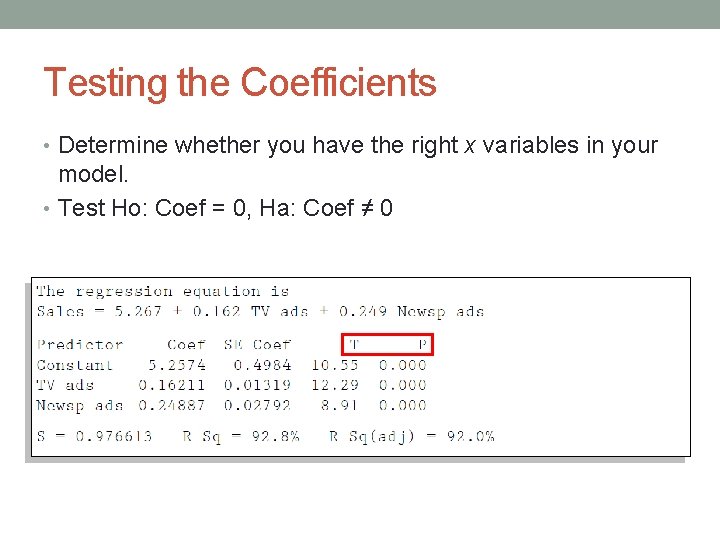
• The interpretation of coefficients are a little more complicated then in simple linear regression. • The coefficient of an x variable in a multiple regression model is the amount by which y changes if that x variable increases by one and the values of all other x variables in the model don’t change. • Plasma TV sales increases by 0. 162 million dollars when TV ad spending increases by $1, 000 and spending on newspaper ads doesn’t change.

Testing the Coefficients • Determine whether you have the right x variables in your model. • Test Ho: Coef = 0, Ha: Coef ≠ 0

Extrapolation: no-no • Do not estimate y for values of x outside their range! • There is no guarantee that the relationship you found follows the same model for distant values of predictors.

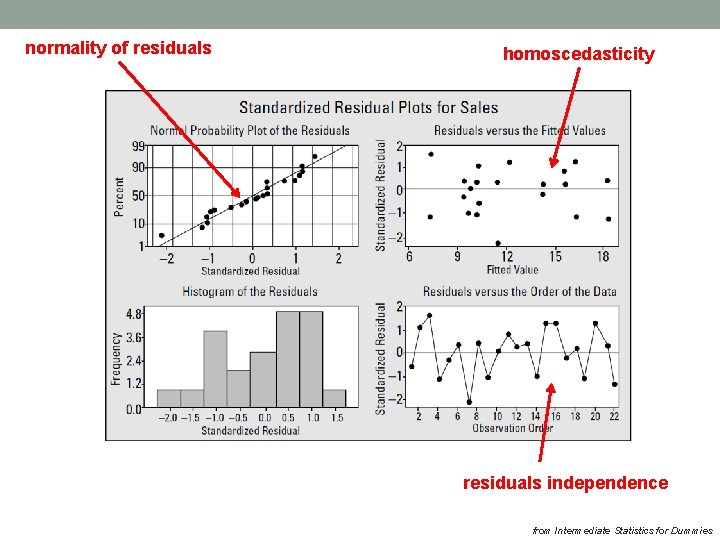
Checking the fit of model The residuals have a normal distribution with mean zero. 2. The residuals have the same variance for each fitted (predicted) value of y. 3. The residuals are independent (don’t affect each other). 1.

normality of residuals homoscedasticity residuals independence from Intermediate Statistics for Dummies

Adjusted R 2 • How well the regression line approximates the real data points is measured by the coefficient of determination R 2 = r 2. • It tells you how much the variability in the y-value is explained by the model. • R 2 increases as we increase the number of variables in the model. • As such, R 2 alone cannot be used as a meaningful comparison of models with different numbers of independent variables – adjusted R 2.