Possible optimization of antiproton injection to the Recycler

Possible optimization of antiproton injection to the Recycler A. Shemyakin MI departmental meeting January 20, 2009

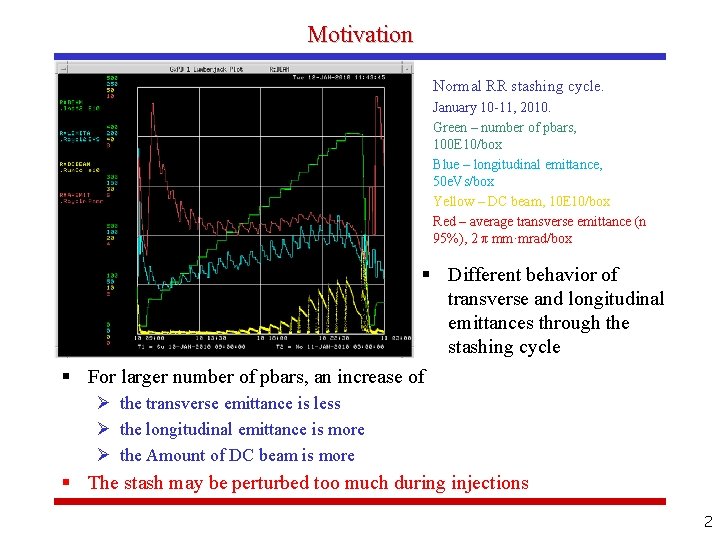
Motivation Normal RR stashing cycle. January 10 -11, 2010. Green – number of pbars, 100 E 10/box Blue – longitudinal emittance, 50 e. Vs/box Yellow – DC beam, 10 E 10/box Red – average transverse emittance (n 95%), 2 π mm·mrad/box § Different behavior of transverse and longitudinal emittances through the stashing cycle § For larger number of pbars, an increase of Ø the transverse emittance is less Ø the longitudinal emittance is more Ø the Amount of DC beam is more § The stash may be perturbed too much during injections 2

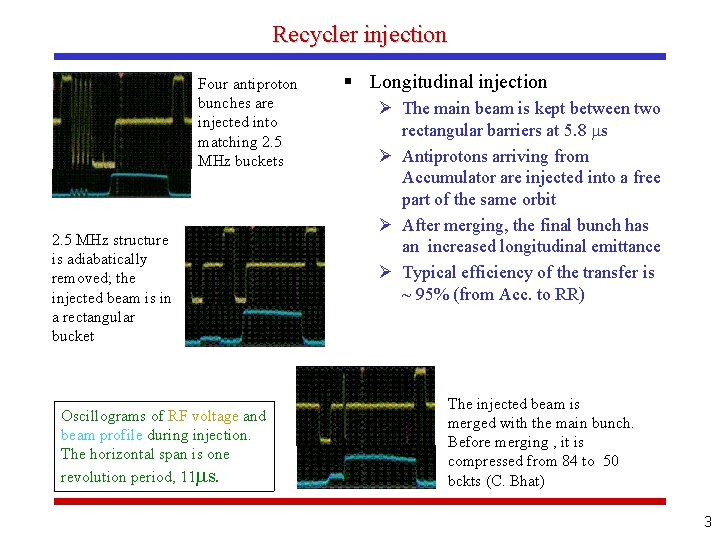
Recycler injection Four antiproton bunches are injected into matching 2. 5 MHz buckets 2. 5 MHz structure is adiabatically removed; the injected beam is in a rectangular bucket Oscillograms of RF voltage and beam profile during injection. The horizontal span is one revolution period, 11 s. § Longitudinal injection Ø The main beam is kept between two rectangular barriers at 5. 8 s Ø Antiprotons arriving from Accumulator are injected into a free part of the same orbit Ø After merging, the final bunch has an increased longitudinal emittance Ø Typical efficiency of the transfer is ~ 95% (from Acc. to RR) The injected beam is merged with the main bunch. Before merging , it is compressed from 84 to 50 bckts (C. Bhat) 3

Direction of optimization Effective potential § S, µs Effective potential S, µs When the barrier between the stash and the injected portion collapses, action of all particles increases approximately as the ratio of final and initial length of synchrotron trajectory. § If longitudinal phase densities and momentum spreads are the same in two portions, the final rms emittance is a sum of their emittances § Present scheme is optimized for relatively hot pbars from Accumulator and a low number of pbars in the stash Ø To illustrate the dependence on the density of the injected beam, consider the ultimate case, when only several pbars are injected. The optimum scenario is to compress the injection bucket before merging to do not perturb the stash and do not care about injected particles. 4

Model Effective potential L in L 0 S, µs Effective potential S, µs § A model for simple estimations: Ø Rectangular bucket (infinite RF voltage) Ø Instantaneous drop of the separation between injected and main bunches § What is the optimum length Lin to minimize the final rms emittance? Ø Final rms energy spread σ1 is Ø The final emittance • Indexes 1, 0, and IN correspond to the final stash, initial stash, and injected portion • N – number of pbars, L- bunch length, ε – longitudinal emittance 5

Model (cont. ) Ø The ratio of final –to-initial emittances Ø The final emittance is minimal at the optimal length • Changes with the stash increase Ø …and this minimal value is 6

Numbers § Typical numbers in operation Ø Two parcels in one injection cycle, (9+6)E 10, (6+6) e. Vs Ø Cold bucket length 308 bckts • Effective length for an rms particle ~310 bckts Ø Phase densities • Roughly the same in the beginning of a stashing cycle and very different at the end § Optimum length changes from 31 to 12 bckts § In a real bucket, particles penetrate the barriers Ø To compare with the model, one can consider an effective bucket length, a length of a rectangular bucket where a particle with an rms energy offset has the same action as in a real one Ø For back-to back 48 -bckts barriers and εin = 6 e. Vs, effective length = 18 bckts Ø In the present injection scenario, the effective length ~50 bckts 7

Proposal § Because cooling is more difficult and life time has problems primarily at high stashes, I propose to try injections with preliminary compression of the injection bucket to zero length Ø Probably, for a stashing cycle § Intermediate criteria of improvement would be the dynamics of the longitudinal emittance and DC beam § Final criterion is the average life time (at the same percentage of extracted beam) 8