Positive Thinker Creative Entrepreneur Independent Learner Reflective Learner

Positive Thinker Creative Entrepreneur Independent Learner Reflective Learner Enterprise Skills LESSON OBJECTIVES Responsible Citizen Team Worker Which ones are you using? Always aim high! We are learning to: - Enhance our Mathematical learning skills. (Which Enterprise skills? ) - Accurately calculate the experimental probability of events occurring. (Level 6) Where are we in our journey? AUTHOR www. mistrymaths. co. uk Real life cross/curricular links?

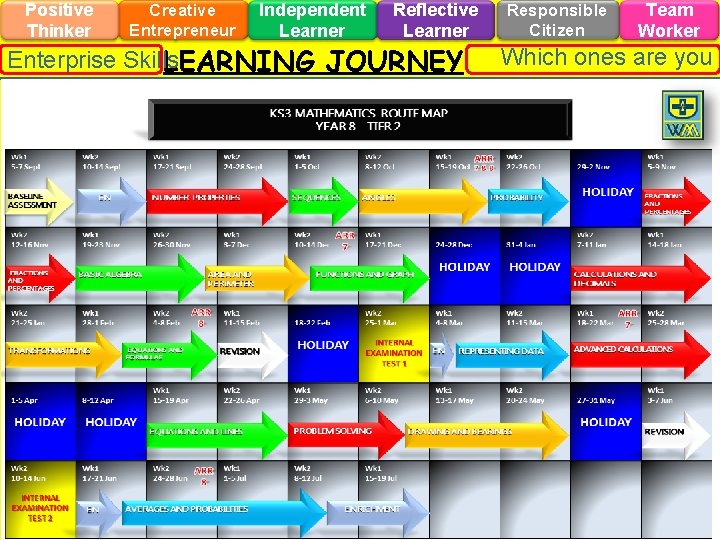
Positive Thinker Creative Entrepreneur Independent Learner Reflective Learner Enterprise Skills LEARNING JOURNEY Responsible Citizen Team Worker Which ones are you using?

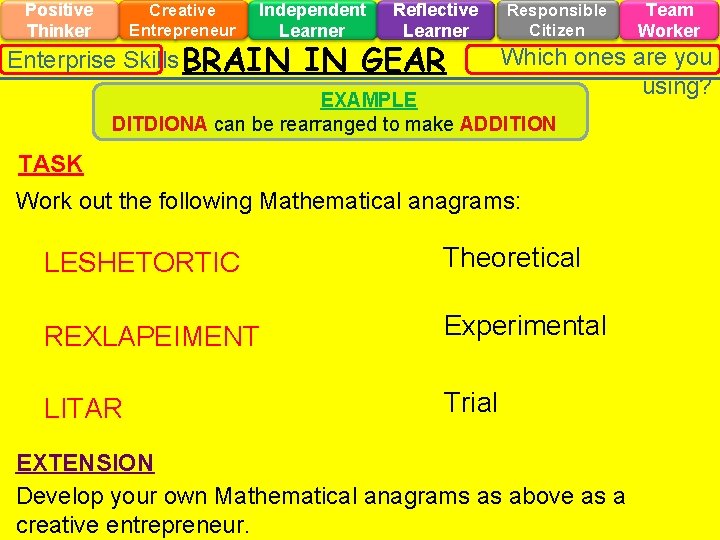
Positive Thinker Creative Entrepreneur Independent Learner Enterprise Skills BRAIN Reflective Learner IN GEAR Responsible Citizen Team Worker Which ones are you using? EXAMPLE DITDIONA can be rearranged to make ADDITION TASK Work out the following Mathematical anagrams: LESHETORTIC Theoretical REXLAPEIMENT Experimental LITAR Trial EXTENSION Develop your own Mathematical anagrams as above as a creative entrepreneur.

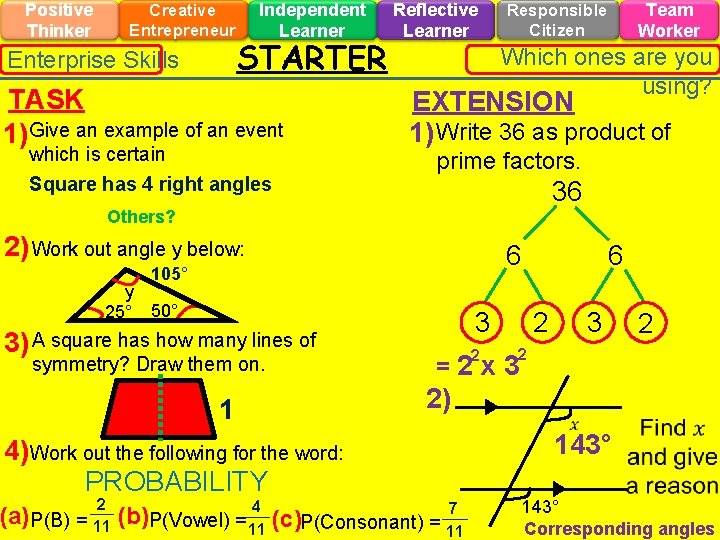
Positive Thinker Creative Entrepreneur Enterprise Skills Independent Learner STARTER TASK 1) Give an example of an event which is certain Square has 4 right angles Reflective Learner Which ones are you using? EXTENSION 1) Write 36 as product of prime factors. 36 Others? 2) Work out angle y below: 6 105° y 25° 50° 3) A square has how many lines of symmetry? Draw them on. 1 3 2 6 2 3 2 2 =2 x 3 2) 143° 4) Work out the following for the word: PROBABILITY 2 Team Worker Responsible Citizen 4 (a) P(B) = 11 (b)P(Vowel) = 11 (c)P(Consonant) = 7 11 143° Corresponding angles

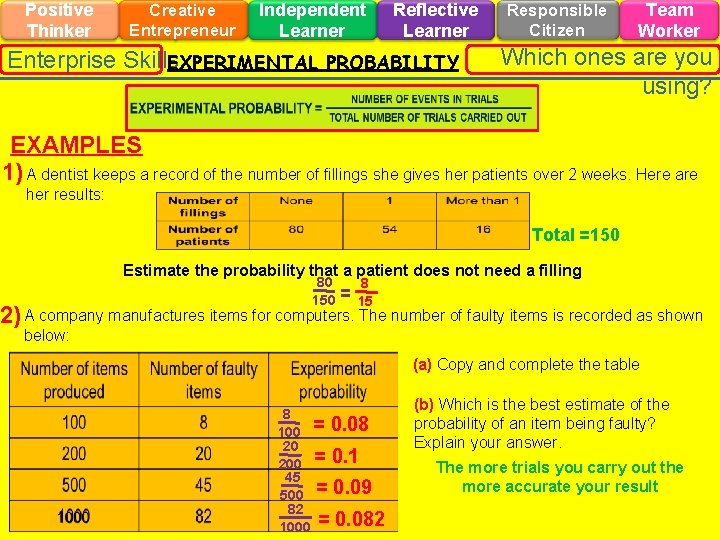
Positive Thinker Creative Entrepreneur Independent Learner Enterprise Skills EXPERIMENTAL Reflective Learner PROBABILITY Responsible Citizen Team Worker Which ones are you using? EXAMPLES 1) A dentist keeps a record of the number of fillings she gives her patients over 2 weeks. Here are her results: Total =150 Estimate the probability that a patient does not need a filling 80 150 = 8 15 2) A company manufactures items for computers. The number of faulty items is recorded as shown below: (a) Copy and complete the table 8 100 = 0. 08 20 200 = 0. 1 45 500 = 0. 09 82 1000 = 0. 082 (b) Which is the best estimate of the probability of an item being faulty? Explain your answer. The more trials you carry out the more accurate your result

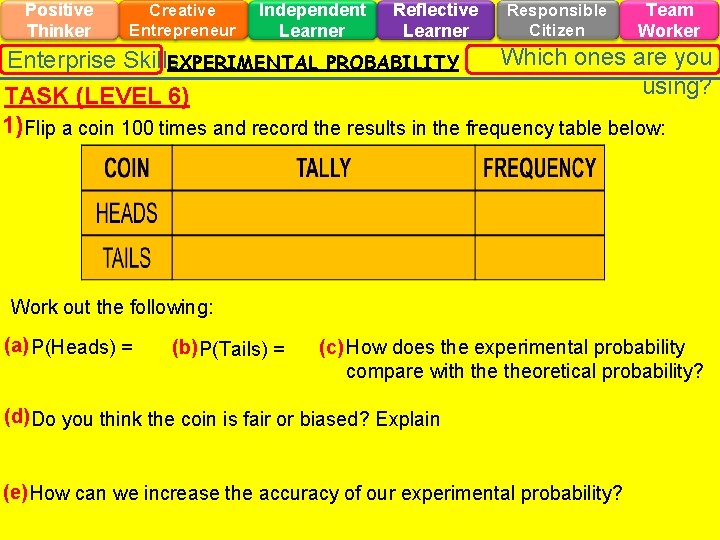
Positive Thinker Creative Entrepreneur Independent Learner Reflective Learner Responsible Citizen Team Worker Which ones are you Enterprise Skills EXPERIMENTAL PROBABILITY using? TASK (LEVEL 6) 1)Flip a coin 100 times and record the results in the frequency table below: Work out the following: (a) P(Heads) = (b) P(Tails) = (c) How does the experimental probability compare with theoretical probability? (d) Do you think the coin is fair or biased? Explain (e) How can we increase the accuracy of our experimental probability?

Positive Thinker Creative Entrepreneur Independent Learner Reflective Learner Responsible Citizen Team Worker Which ones are you Enterprise Skills EXPERIMENTAL PROBABILITY using? TASK (LEVEL 6) 2)Marie made a five-sided spinner, like the one shown in the diagram. She used it to play a board game with her friend Sarah. The girls thought that the spinner was not very fair as it seemed to land on some numbers more than others. They threw the spinner 200 times and recorded the results. TOTAL = 200 (a) Work out the experimental probability of each number. 19 27 32 P(1) = 200 P(2) = 200 P(3) = 200 = 4 25 53 69 P(4) = 200 P(5) = 200 (b) How many times would you expect each number to occur if the spinner 1 of 200 = 40 is fair? 5

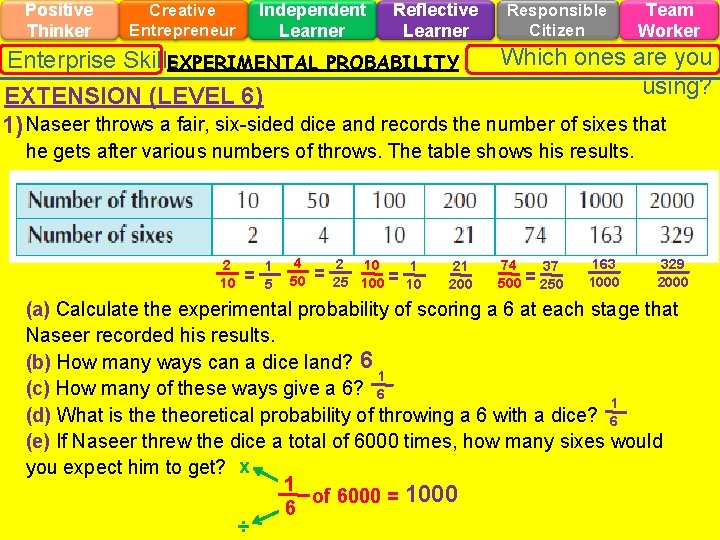
Positive Thinker Independent Learner Creative Entrepreneur Reflective Learner Responsible Citizen Team Worker Which ones are you Enterprise Skills EXPERIMENTAL PROBABILITY using? EXTENSION (LEVEL 6) 1) Naseer throws a fair, six-sided dice and records the number of sixes that he gets after various numbers of throws. The table shows his results. 2 10 = 1 5 4 50 = 2 10 1 = 25 100 10 21 200 74 37 = 500 250 163 1000 329 2000 (a) Calculate the experimental probability of scoring a 6 at each stage that Naseer recorded his results. (b) How many ways can a dice land? 6 1 (c) How many of these ways give a 6? 6 1 (d) What is theoretical probability of throwing a 6 with a dice? 6 (e) If Naseer threw the dice a total of 6000 times, how many sixes would you expect him to get? x 1 of 6000 = 1000 6 ÷

Positive Thinker Creative Entrepreneur Independent Learner Reflective Learner Responsible Citizen Team Worker Which ones are you Enterprise Skills EXPERIMENTAL PROBABILITY using? THE CHECKOUT GAME RULES 1) This is a two-player game. Each player receives 12 tokens representing music CDs. 2) Each player places the tokens in any of the checkout aisles marked 1 -12 in the store on his/her side of the board. Choose any of the aisles you desire, putting any number of tokens on a space as you would like. 3) Take turns rolling two dice. On each roll, determine the sum of the dice. If you have CDs in that numbered checkout aisle, move one CD to the parking lot. 4) The winner is determined by the first player to have all of their CDs in the parking lot. TASK What is the best arrangement for the CDs?

Positive Thinker Creative Entrepreneur Independent Learner Reflective Learner Responsible Citizen Team Worker Sound Store 9 10 8 7 6 5 4 3 2 1 Parking Lot 8 7 6 5 4 3 2 1 Music Mart 9 10 11 12 Which ones are you Enterprise Skills EXPERIMENTAL PROBABILITY using? THE CHECKOUT GAME PLAYER 1 PLAYER 2

Positive Thinker Creative Entrepreneur Independent Learner Reflective Learner Responsible Citizen Team Worker Which ones are you Enterprise Skills EXPERIMENTAL PROBABILITY using? POSSIBILITY SPACE FOR CHECKOUT GAME DICE 1 DICE 2 + 1 2 3 4 5 6 7 8 9 4 5 6 7 8 9 10 11 12 36 Outcomes (numbers in black) Work out the probability for each checkout aisle number 1 36 2 P(3) = 36 3 P(4) = 36 5 P(6) = 36 6 P(7) = 36 5 36 4 1 P(9) = 36 = 9 3 1 P(10) = 36 = 12 2 1 P(11) = 36 = 18 1 P(12) = 36 P(8) = P(2) = 18 1 = 12 = 1 6 1 2 12 1 P(Multiple of 3) = 36 = 3 18 1 P(Odd sum) = 36 = 2 30 5 P(Sum ≥ 5) = 36 = 6 15 5 P(Sum < 7) = 36 = 12 P(Even) = 18 36 =

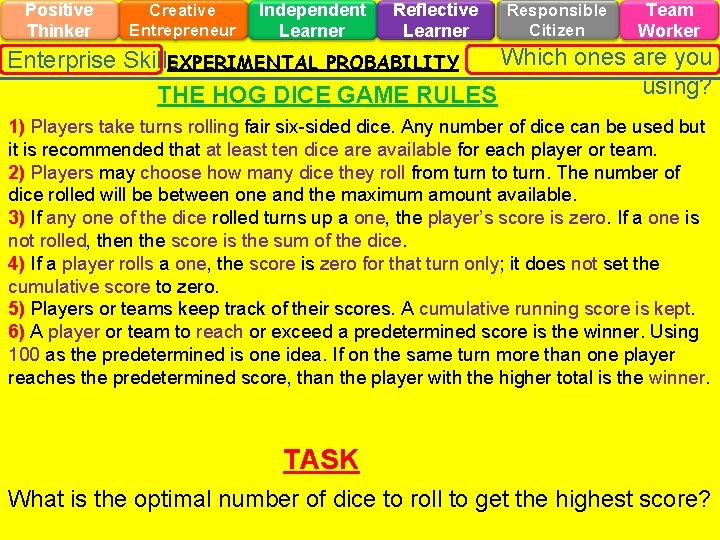
Positive Thinker Creative Entrepreneur Independent Learner Reflective Learner Responsible Citizen Team Worker Which ones are you Enterprise Skills EXPERIMENTAL PROBABILITY using? THE HOG DICE GAME RULES 1) Players take turns rolling fair six-sided dice. Any number of dice can be used but it is recommended that at least ten dice are available for each player or team. 2) Players may choose how many dice they roll from turn to turn. The number of dice rolled will be between one and the maximum amount available. 3) If any one of the dice rolled turns up a one, the player’s score is zero. If a one is not rolled, then the score is the sum of the dice. 4) If a player rolls a one, the score is zero for that turn only; it does not set the cumulative score to zero. 5) Players or teams keep track of their scores. A cumulative running score is kept. 6) A player or team to reach or exceed a predetermined score is the winner. Using 100 as the predetermined is one idea. If on the same turn more than one player reaches the predetermined score, than the player with the higher total is the winner. TASK What is the optimal number of dice to roll to get the highest score?

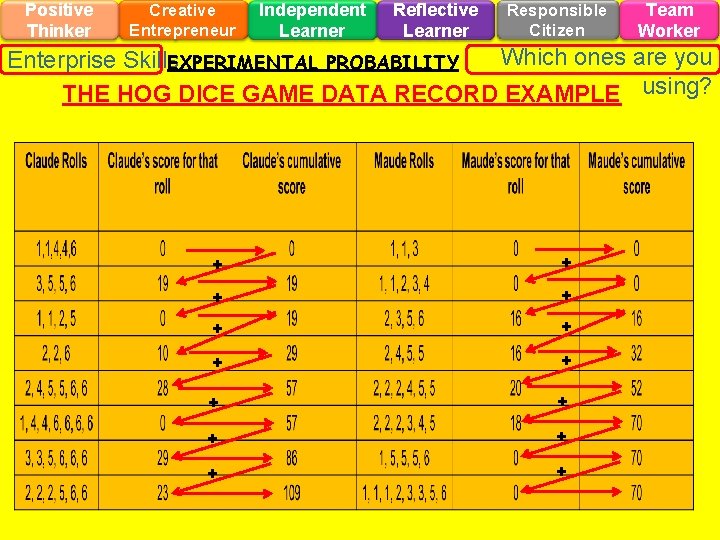
Positive Thinker Creative Entrepreneur Independent Learner Reflective Learner Responsible Citizen Team Worker Which ones are you Enterprise Skills EXPERIMENTAL PROBABILITY THE HOG DICE GAME DATA RECORD EXAMPLE using? + + + +

Positive Thinker Creative Entrepreneur Independent Learner Reflective Learner Responsible Citizen Team Worker Which ones are you Enterprise Skills EXPERIMENTAL PROBABILITY using? THE HOG DICE GAME DATA RECORD SHEET (TEACHER V STUDENTS)

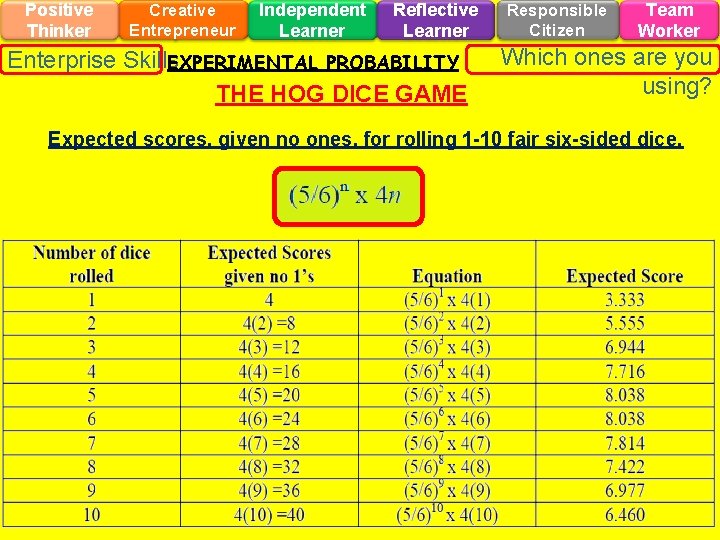
Positive Thinker Creative Entrepreneur Independent Learner Reflective Learner Enterprise Skills EXPERIMENTAL PROBABILITY THE HOG DICE GAME Responsible Citizen Team Worker Which ones are you using? Expected scores, given no ones, for rolling 1 -10 fair six-sided dice.

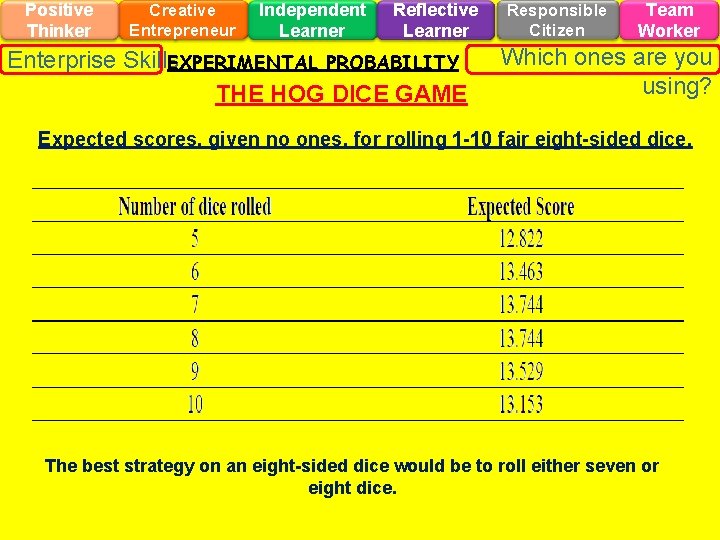
Positive Thinker Creative Entrepreneur Independent Learner Reflective Learner Enterprise Skills EXPERIMENTAL PROBABILITY THE HOG DICE GAME Responsible Citizen Team Worker Which ones are you using? Expected scores, given no ones, for rolling 1 -10 fair eight-sided dice. The best strategy on an eight-sided dice would be to roll either seven or eight dice.

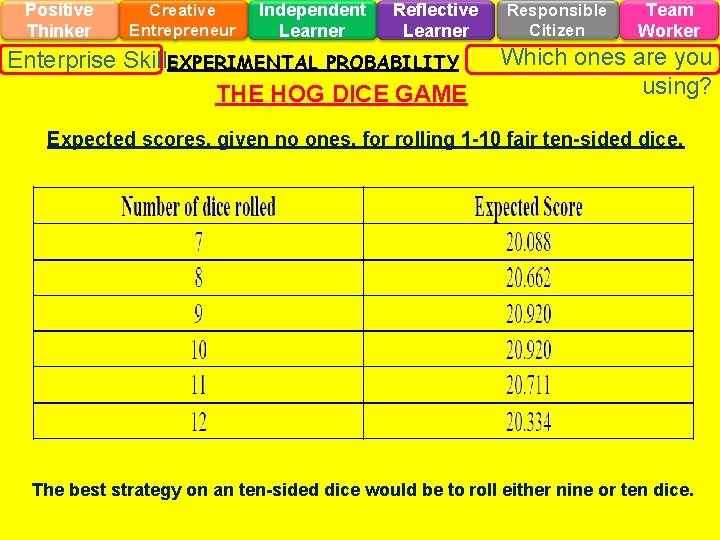
Positive Thinker Creative Entrepreneur Independent Learner Reflective Learner Enterprise Skills EXPERIMENTAL PROBABILITY THE HOG DICE GAME Responsible Citizen Team Worker Which ones are you using? Expected scores, given no ones, for rolling 1 -10 fair ten-sided dice. The best strategy on an ten-sided dice would be to roll either nine or ten dice.

Positive Thinker Creative Entrepreneur Enterprise Skills Independent Learner Reflective Learner DISCOVERY Responsible Citizen Team Worker Which ones are you using? LINK BACK TO OBJECTIVES - Accurately calculate the experimental probability of events occurring. What level are we working at?

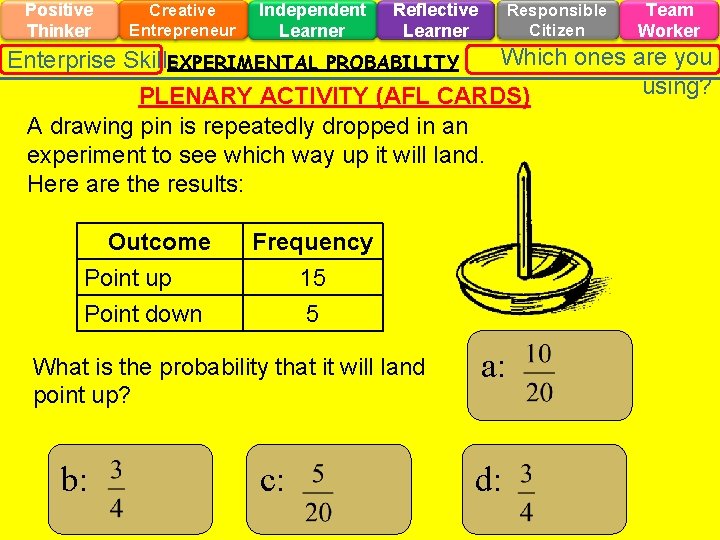
Positive Thinker Creative Entrepreneur Independent Learner Reflective Learner Responsible Citizen Team Worker Which ones are you Enterprise Skills EXPERIMENTAL PROBABILITY using? PLENARY ACTIVITY (AFL CARDS) A drawing pin is repeatedly dropped in an experiment to see which way up it will land. Here are the results: Outcome Point up Point down Frequency 15 5 What is the probability that it will land point up? b: c: a: d:

Positive Thinker Creative Entrepreneur Independent Learner Reflective Learner Responsible Citizen Team Worker Which ones are you Enterprise Skills EXPERIMENTAL PROBABILITY using? PLENARY ACTIVITY (AFL CARDS) A coin is repeatedly thrown 60 times in an experiment to see which way up it will land. Here are the results of the experiment: Outcome Heads Tails Frequency 27 33 a: What is the probability that it will land head up? b: c: d:

Positive Thinker Creative Entrepreneur Independent Learner Reflective Learner Responsible Citizen Team Worker Which ones are you Enterprise Skills EXPERIMENTAL PROBABILITY using? PLENARY ACTIVITY (AFL CARDS) Here are the results of a survey of cars passing a school: Colour Red Black Silver Other b: Number of What is the probability of the next car passing the school being cars silver? (Simplify answer) 3 10 15 a: 2 c: d:

Positive Thinker Creative Entrepreneur Independent Learner Reflective Learner Responsible Citizen Team Worker Which ones are you Enterprise Skills EXPERIMENTAL PROBABILITY using? PLENARY ACTIVITY (AFL CARDS) Here are the results of a survey of cars passing a school: What is the probability of the Colour Number of next car passing the cars school being black? (Simplify answer) Red 3 Black 10 Silver 15 a: Other 2 b: c: d:

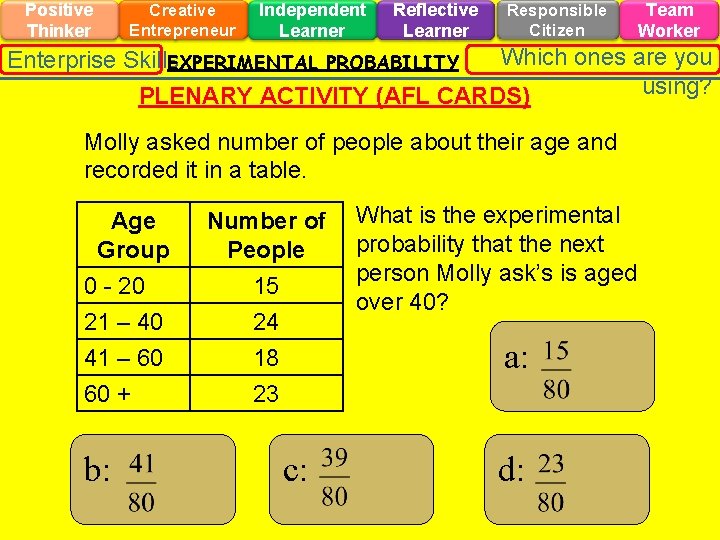
Positive Thinker Creative Entrepreneur Independent Learner Reflective Learner Responsible Citizen Team Worker Which ones are you Enterprise Skills EXPERIMENTAL PROBABILITY using? PLENARY ACTIVITY (AFL CARDS) Molly asked number of people about their age and recorded it in a table. Age Group 0 - 20 21 – 40 41 – 60 60 + b: Number of People 15 24 18 23 c: What is the experimental probability that the next person Molly ask’s is aged over 40? a: d:

Positive Thinker Creative Entrepreneur Independent Learner Reflective Learner Responsible Citizen Team Worker Which ones are you Enterprise Skills EXPERIMENTAL PROBABILITY using? PLENARY ACTIVITY (AFL CARDS) An ice cream shop recorded the number of customers purchasing ice creams of each of the four flavours available. Flavour Vanilla Chocolate Strawberry Peach b: Number of Customers 12 18 9 11 c: What is the experimental probability that the next customer will purchase a Vanilla or chocolate ice cream? a: d:

Positive Thinker Creative Entrepreneur Independent Learner Reflective Learner Responsible Citizen Team Worker Which ones are you Enterprise Skills EXPERIMENTAL PROBABILITY using? PLENARY ACTIVITY (AFL CARDS) Here are the results of a survey of cars passing a school: What is the probability of the Colour Number of next car passing the cars school being Red or other? (Simplify answer) Red 3 Black 10 Silver 15 a: Other 2 b: c: d:

What have you learnt? Draw your brain In your brain, write or draw everything you can remember about calculating the experimental probability of events occurring. It can be a skill or a reflection, or something else that might be prominent in your brain. Where are we in our journey? What level are we working at?

Positive Thinker Creative Entrepreneur Independent Learner Reflective Learner Responsible Citizen Team Worker Which ones are you Enterprise Skills. SELF ASSESSMENT Plenary using? Activity How well do you understand the task? . I don’t understand I nearly understand www. mistrymaths. co. uk I fully understand

Positive Thinker Creative Entrepreneur Independent Learner Reflective Learner Enterprise Skills. SELF ASSESSMENT Plenary Activity WWW (What Went Well) EBI (Even Better If) On your post it notes… Think about how you can improve your work. www. mistrymaths. co. uk Responsible Citizen Team Worker Which ones are you using?