Positive Semidefinite matrix A is a positive semidefinite



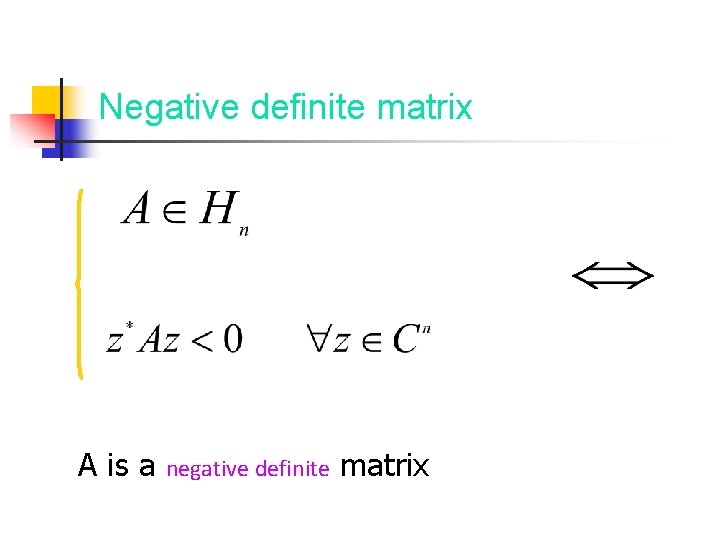










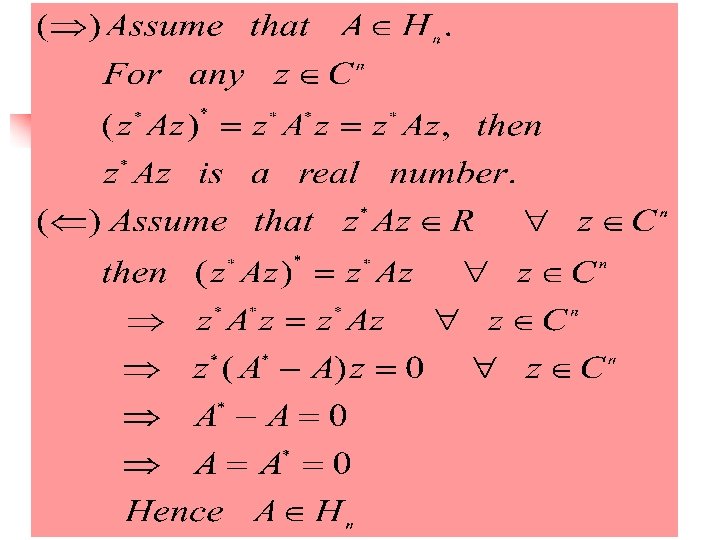

























- Slides: 43

Positive Semidefinite matrix A is a positive semidefinite (also called matrix nonnegative definite matrix)

Positive definite matrix A is a positive definite matrix

Negative semidefinite matrix A is a negative semidefinite matrix
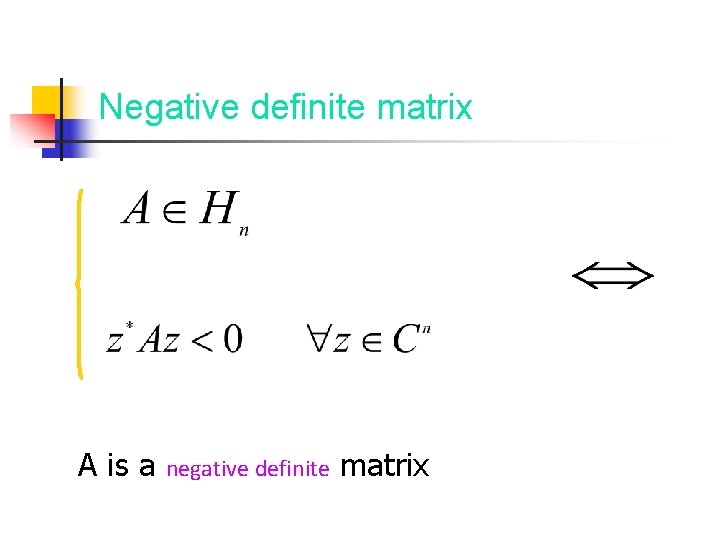
Negative definite matrix A is a negative definite matrix

Positive semidefinite matrix A is real symmetric matrix A is a positive semidefinite matrix

Positive definite matrix A is real symmetric matrix A is a positive definite matrix

Question Is It true that ? Yes

Proof of Question ?

Proof of Question ?

Fact 1. 1. 6 n The eigenvalues of a Hermitian (resp. positive semidefinite , positive definite) matrix are all real (resp. nonnegative, positive)

Proof of Fact 1. 1. 6

Exercise From this exercise we can redefinite: H is a positive semidefinite

注意 A is symmetric

注意 之反例 is not symmetric
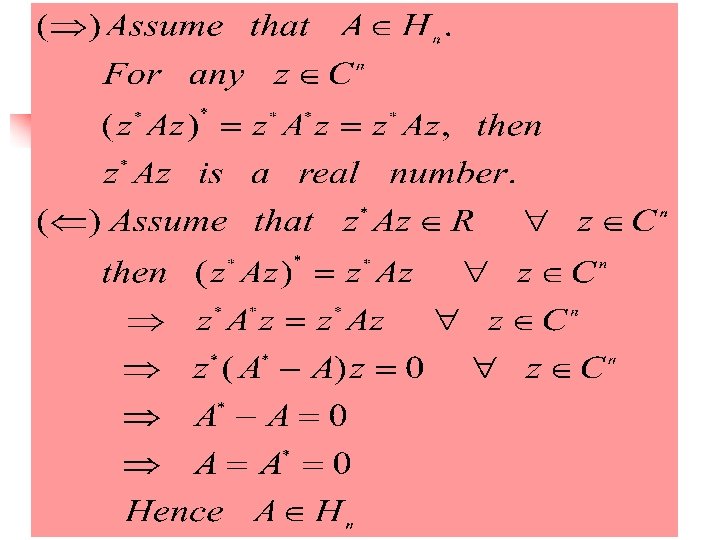
Proof of Exercise

Remark n n Let A be an nxn real matrix. If λ is a real eigenvalue of A, then there must exist a corresponding real eigenvector. However, if λ is a nonreal eigenvalue of A, then it cannot have a real eigenvector.

Explain of Remark n p. 1 A, λ : real Az= λz, 0≠z (A- λI)z=0 By Gauss method, we obtain that z is a real vector.

Explain of Remark n p. 2 A: real, λ is non-real Az= λz, 0≠z z is real, which is impossible

Elementary symmetric function kth elementary symmetric function

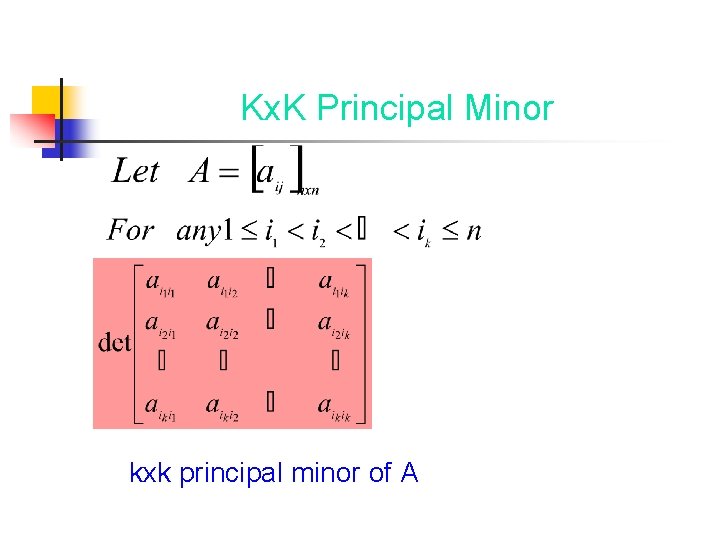
Kx. K Principal Minor kxk principal minor of A

Lemma p. 1

Lemma p. 2

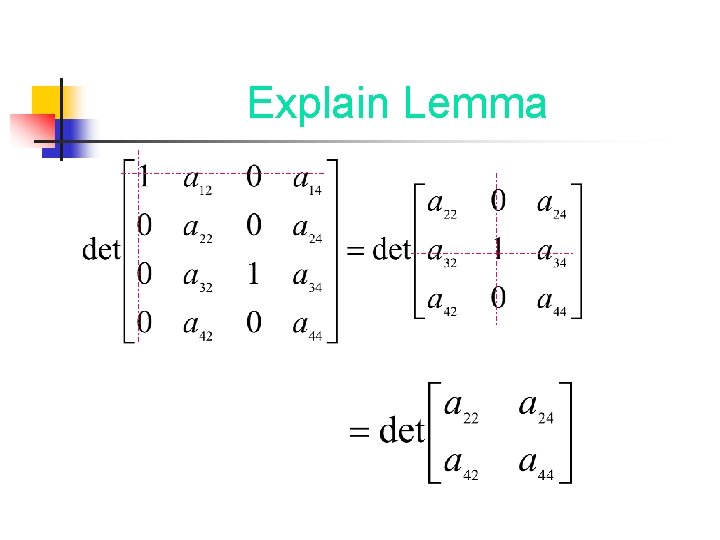
Explain Lemma

The Sum of Kx. K Principal Minors

Theorem

Proof of Theorem p. 1

Proof of Theorem p. 2

Rank P. 1 rank. A: =the maximun number of linear independent column vectors =the dimension of the column space result = the maximun number of linear independent row vectors result =the dimension of the row space

Rank P. 2 rank. A: =the number of nonzero rows in a row-echelon (or the reduced row echlon form of A)

Rank P. 3 rank. A: =the size of its largest nonvanishing minor (not necessary a principal minor) See next page =the order of its largest nonsigular submatrix.

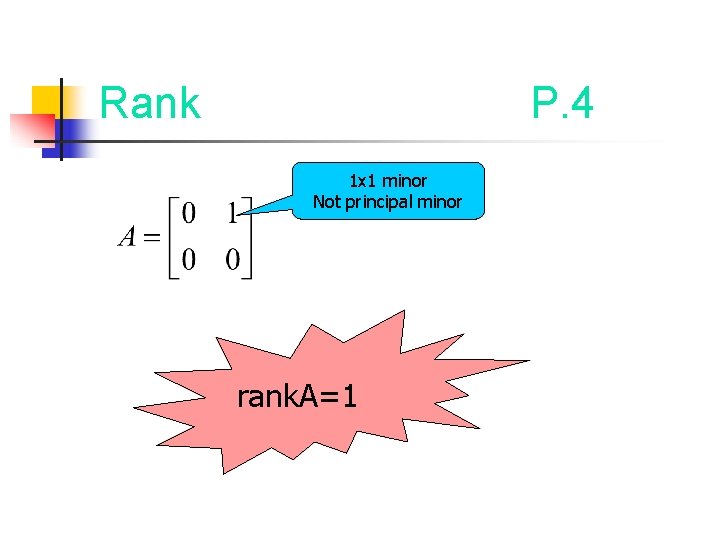
Rank P. 4 1 x 1 minor Not principal minor rank. A=1

Theorem Let A be an nxn sigular matrix. Let s be the algebraic multiple of eigenvalue 0 of A. Then A has at least one nonsingular (nonzero)principal submatrix(minor) of order n-s.

Proof of Theorem p. 1

Geometric multiple Let A be a square matrix and λ be an eigenvalue of A, then the geometric multiple of λ=dim. N(λI-A) the eigenspace of A corresponding to λ

Diagonalizable

Exercise A and have the same characteristic polynomial and moreover the geometric multiple and algebraic multiple are similarily invariants.

Proof of Exercise p. 1

Proof of Exercise (2)Since A and p. 2 have the same characteristic polynomial, they have the same eigenvalues and the algebraic multiple of each eigenvalue is the same.

Proof of Exercise p. 3

Explain: geom. mult=alge. mult in diagonal matrix

Fact For a diagonalizable(square) matrix, the algebraic multiple and the geometric multiple of each of its eigenvalues are equal.

Corollary Let A be a diagonalizable(square) matrix and if r is the rank of A, then A has at least one nonsingular principal Submatrix of order r.

Proof of Corollary p. 1
 Positive semidefinite matrix
Positive semidefinite matrix Transpose of symmetric matrix
Transpose of symmetric matrix Orthogonal matrix example 3x3
Orthogonal matrix example 3x3 Semmelweis university faculty of medicine
Semmelweis university faculty of medicine Filetype:pdf
Filetype:pdf Skew symmetric matrix
Skew symmetric matrix Perpendicular matrix
Perpendicular matrix Fluid matrix
Fluid matrix Matrix rules
Matrix rules Dissimilarity matrix
Dissimilarity matrix All staphylococci are catalase positive
All staphylococci are catalase positive Positive + positive equals
Positive + positive equals Positive practice positive outcomes
Positive practice positive outcomes Nasa risk matrix
Nasa risk matrix Ifta matrix
Ifta matrix Cofactors of determinants
Cofactors of determinants Coriolis matrix
Coriolis matrix Julia covariance matrix
Julia covariance matrix Source message and channel factors
Source message and channel factors Unit 1 algebra basics homework 6 matrices
Unit 1 algebra basics homework 6 matrices Question mark bcg
Question mark bcg Orthographic projection definition
Orthographic projection definition Ie matrix
Ie matrix Mixing matrix
Mixing matrix Ce6602 structural analysis 2
Ce6602 structural analysis 2 Geometric camera calibration
Geometric camera calibration Lorentz transformation matrix
Lorentz transformation matrix Confusion matrix stata
Confusion matrix stata Epipolar
Epipolar Matrices for dummies
Matrices for dummies Cramers rule
Cramers rule Designing adaptive organizations
Designing adaptive organizations Yale representation of sparse matrix
Yale representation of sparse matrix Transformasi matriks 3x3
Transformasi matriks 3x3 Haddon matrix examples
Haddon matrix examples Sicher sutural theory
Sicher sutural theory Spm design matrix
Spm design matrix Introduction to matlab lab report
Introduction to matlab lab report Labmetrics
Labmetrics Matrix inverse worksheet
Matrix inverse worksheet A nine box matrix requires assessing employees on ________.
A nine box matrix requires assessing employees on ________. Tradurre
Tradurre Search engines architecture
Search engines architecture Matrices formula
Matrices formula