Positive definite matrices Quadratic form of a positive

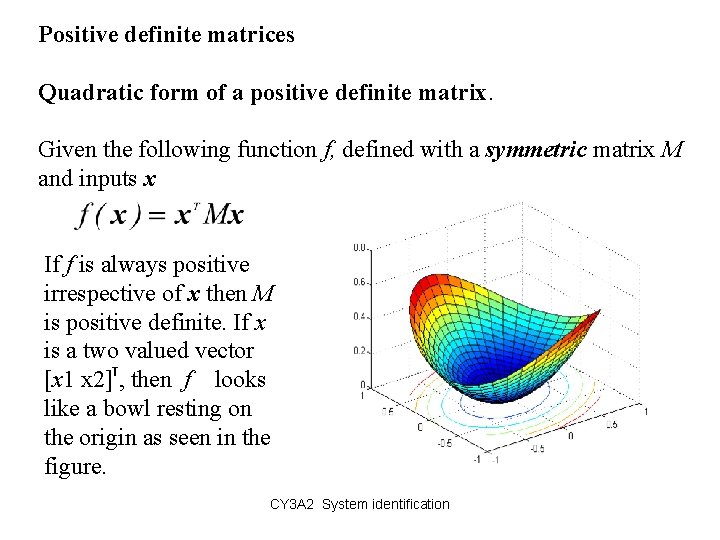
Positive definite matrices Quadratic form of a positive definite matrix. Given the following function f, defined with a symmetric matrix M and inputs x If f is always positive irrespective of x then M is positive definite. If x is a two valued vector [x 1 x 2]T, then f looks like a bowl resting on the origin as seen in the figure. CY 3 A 2 System identification

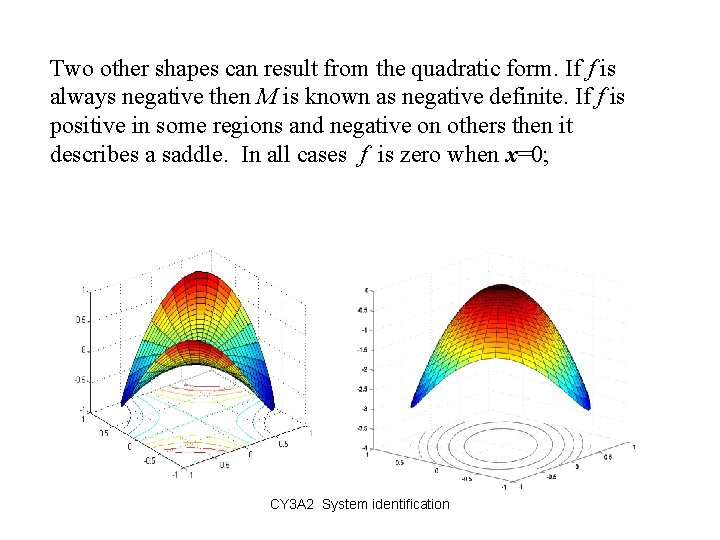
Two other shapes can result from the quadratic form. If f is always negative then M is known as negative definite. If f is positive in some regions and negative on others then it describes a saddle. In all cases f is zero when x=0; CY 3 A 2 System identification

Theorem: If a matrix definite then it is positive Proof. The quadratic form is If we can show that f is always positive then M must be positive definite. We can write this as Provided that Ux always gives a non zero vector for all values of x except when x=0 we can write b = U x, i. e. so f must always be positive CY 3 A 2 System identification

Least squares linear regression Courtesy of Johann Fredrich Carl Gauss Given a model and some data, we wish to calculate the ‘best’ coefficients. One way is to minimise the errors. CY 3 A 2 System identification

Consider a model of the form (first model) We can write this in matrix form by putting all the data into a model output vector , the parameters into a vector CY 3 A 2 System identification

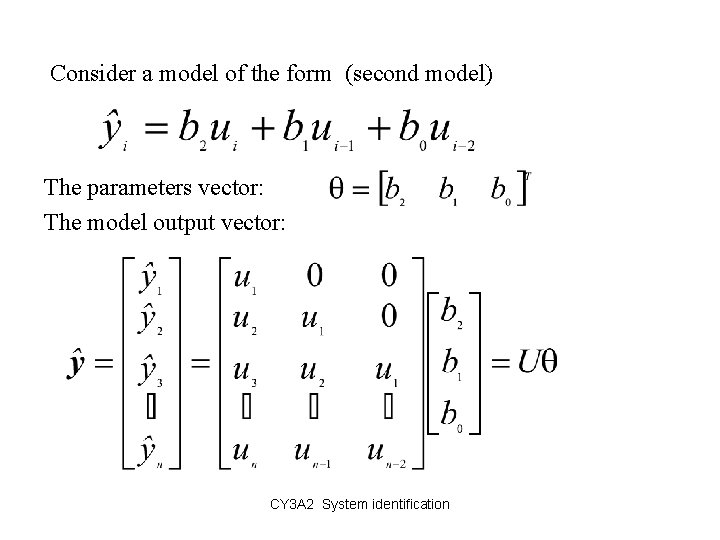
Consider a model of the form (second model) The parameters vector: The model output vector: CY 3 A 2 System identification

The actual output vector A model can be estimated by using as a target of y --- actual output (measurements) --- the output that is expected by the model The model parameter θ is derived so that the distance between these two vectors is the smallest possible. CY 3 A 2 System identification

In vector form CY 3 A 2 System identification

Rearrange this as follows 1. Only the last term (which is in quadratic form) contains θ, 2. is positive definite. CY 3 A 2 System identification

SSE has the minimum (best fit) (the at hat ^ means estimate) is the solution of least square parameter estimate. CY 3 A 2 System identification

An alternative proof: CY 3 A 2 System identification