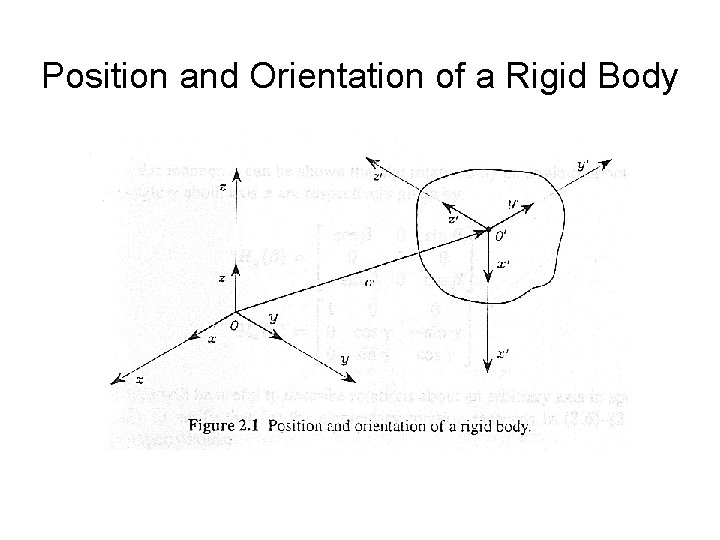
Position and Orientation of a Rigid Body Position

Position and Orientation of a Rigid Body

Position and Orientation of a Rigid Body Ø The position of origin O’ with respect to O-xyz is expressed by the relation Ø The component of each unit vector are the direction cosines of the axes of frame O’-x’y’z’

Rotation Matrix Ø Orientation can be described by rotation matrix Ø R is orthogonal matrix

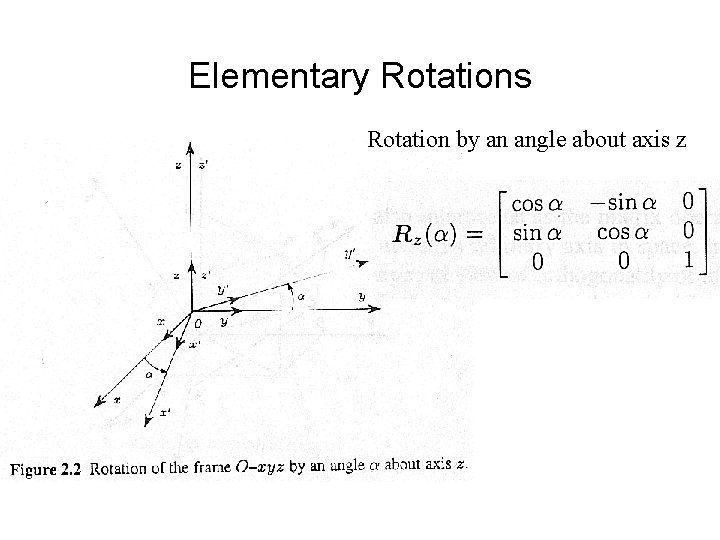
Elementary Rotations Rotation by an angle about axis z

Elementary Rotations Ø Rotation by an angle about axis y Ø Rotation by an angle about axis x

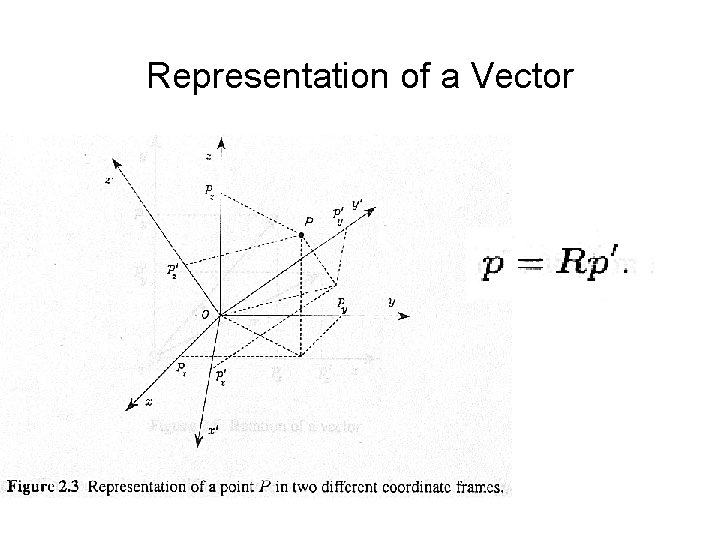
Representation of a Vector

Representation of a Vector Ø Representation of p w. r. t O-xyz Ø Representation of p w. r. t O -x’y’z’

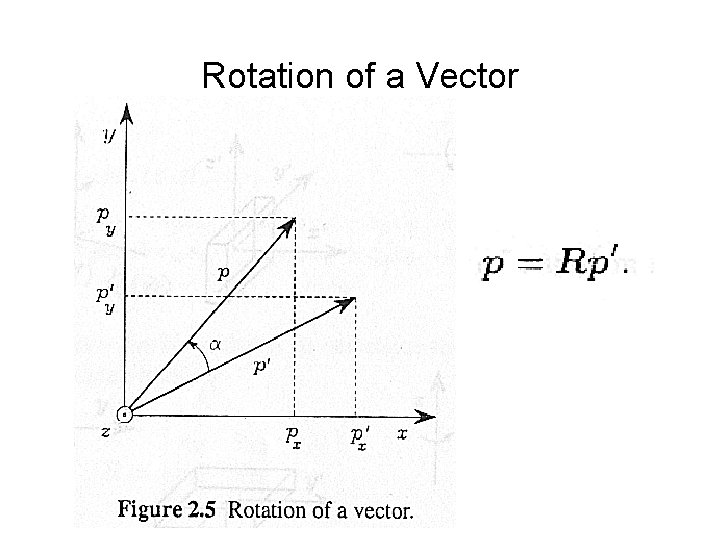
Rotation of a Vector

Equivalent Geometrical Meanings of Rotation Matrix

Composition of Rotation Matrices Ø Let Rij denote the rotation matrix of Frame i with respect to Frame j Ø Post-multiplication interpretation ØRefer to current frame Ø Pre-multiplication interpretation ØRefer to fixed frame

Euler Angles Ø Minimal representation of orientation Ø Three parameters are sufficient Ø Euler Angles Ø Two successive rotations are not made about parallel axes Ø How many kinds of Euler angles are there?

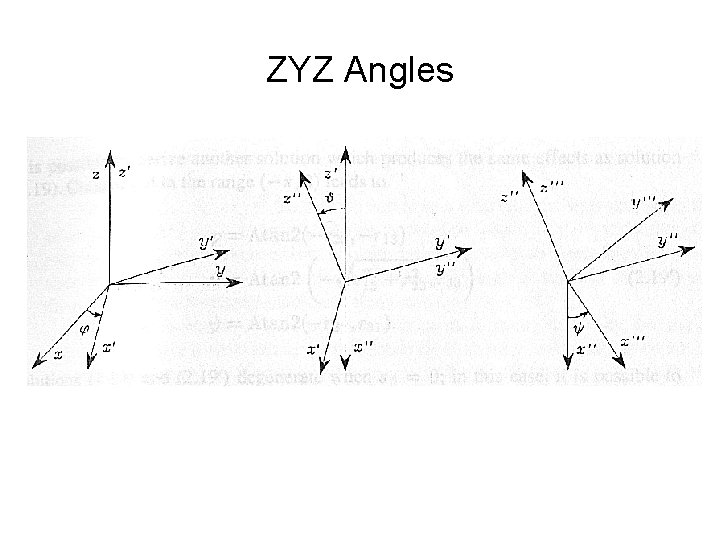
ZYZ Angles Ø The rotation described by ZYZ angles is

ZYZ Angles

ZYZ Angles Ø The rotation matrix is

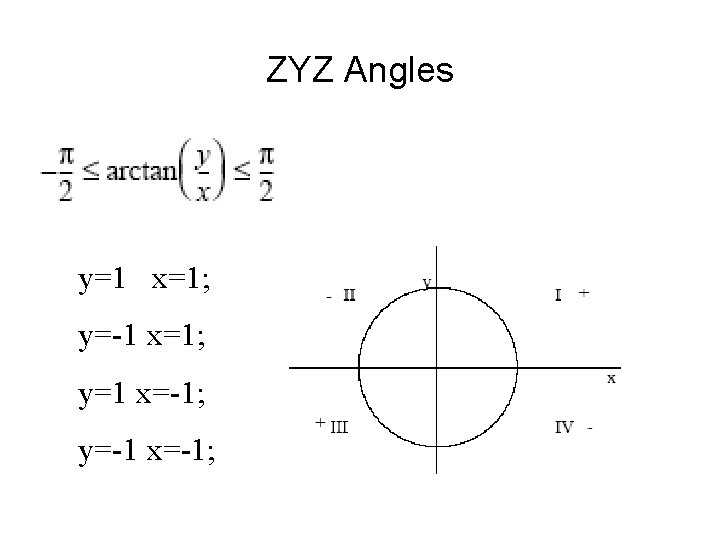
ZYZ Angles Ø Inverse problem: determine the Euler angles corresponding to a given rotation matrix Ø Solution 1: theta is in the range (0, pi)

ZYZ Angles y=1 x=1; y=-1 x=1; y=1 x=-1; y=-1 x=-1;

ZYZ Angles Ø Solution 1: theta is in the range (0, pi)

ZYZ Angles Ø Solution 2: theta is in the range (-pi, 0)

ZYZ Angles Ø What will happen if sin(theta) = 0? Ø Matlab: eul 2 tr, tr 2 eul

Roll-Pitch-Yaw Angles Ø Originate from (aero)nautical field

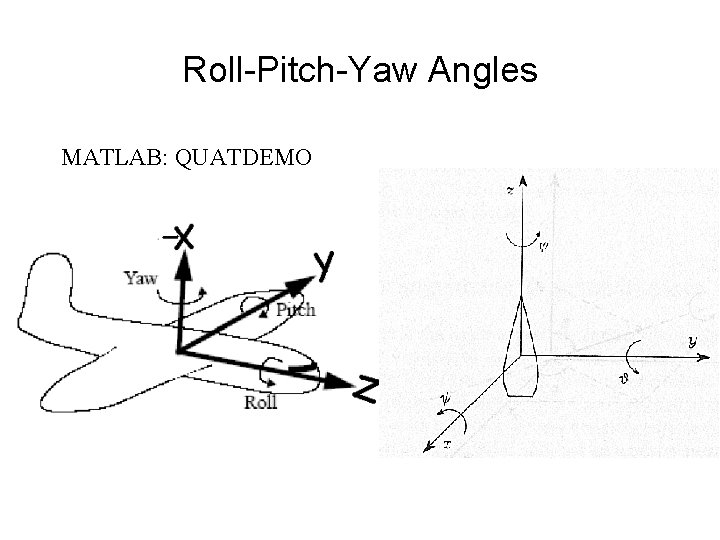
Roll-Pitch-Yaw Angles MATLAB: QUATDEMO

Roll-Pitch-Yaw Angles Ø The rotation matrix is

Roll-Pitch-Yaw Angles Ø Inverse problem: determine the Euler angles corresponding to a given rotation matrix Ø Solution 1: theta is in the range (-pi/2, pi/2)

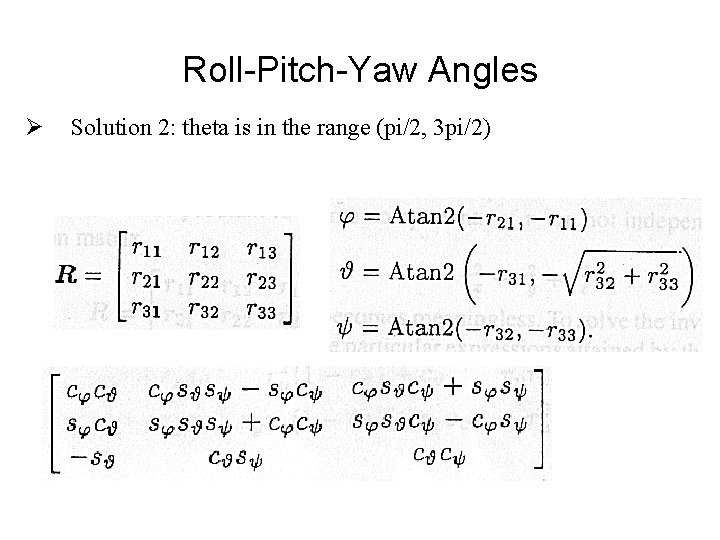
Roll-Pitch-Yaw Angles Ø Solution 2: theta is in the range (pi/2, 3 pi/2)

Roll-Pitch-Yaw Angles Ø What will happen if cos(theta) = 0? Ø Matlab: rpy 2 tr, tr 2 rpy

Angle and Axis Ø Non-minimal representation: four parameters ØThe unit vector of a rotation axis w. r. t O-xyz ØThe angle theta about the axis ØMatlab: quatdemo

Angle and Axis • Align r with z • Rotate by theta about z • Realign with the initial direction of r Attention: always refer to the fixed frame

Angle and Axis Ø The resulting rotation matrix is

Angle and Axis Ø The inverse problem Ø Remember: the three component of r is not independent

Angle and Axis Ø Problems: Ø solution is not unique Ør is arbitrary when theta = 0

Unit Quaternion Ø Unit quaternion is defined as

Unit Quaternion Ø Inverse problem: Ø Matlab: quaternion, plot, quaternion. t