Population synthesis of isolated NSs and tests of

Population synthesis of isolated NSs and tests of cooling curves Sergei Popov (Sternberg Astronomical Institute) Co-authors: D. Blaschke, H. Grigorian, B. Posselt, R. Turolla JINR, Dubna, September 01, 2006

Plan of the talk n n n n Intro. Close-by NSs Population synthesis Solar vicinity. Stars Spatial distribution Mass spectrum Two tests of cooling Brightness constraint Sensitivity of two tests Mass constraint Application to hybrid stars Future plans Age-Distance diagram Final conclusions 2

Isolated neutron stars population: in the Galaxy and at the backyard q INSs appear in many flavours n n n Radio pulsars AXPs SGRs CCOs RINSs RRATs q Local population of young NSs is different (selection) n. Radio pulsars n. Geminga+ 3 n. RINSs

Close-by radioquiet NSs n Discovery: n n Walter et al. (1996) Proper motion and distance: Kaplan et al. No pulsations Thermal spectrum Later on: six brothers RX J 1856. 5 -3754 4

Magnificent Seven Name Period, s RX 1856 - RX 0720 8. 39 RBS 1223 10. 31 RBS 1556 - RX 0806 11. 37 RX 0420 3. 45 RBS 1774 9. 44 Radioquiet (? ) Close-by Thermal emission Long periods 5

Population of close-by young NSs n Magnificent seven n Geminga and 3 EG J 1853+5918 n Four radio pulsars with thermal emission (B 0833 -45; B 0656+14; B 1055 -52; B 1929+10) n Seven older radio pulsars, without detected thermal emission. It is useful to study these stars using the population synthesis technique 6

Population synthesis: ingredients n Birth rate of NSs n Initial spatial distribution n Spatial velocity (kick) n Mass spectrum n Thermal evolution n Interstellar absorption n Detector properties Task: To build an artificial model of a population of some astrophysical sources and to compare the results of calculations with observations. A brief review on population synthesis in astrophysics can be found in astro-ph/0411792 7

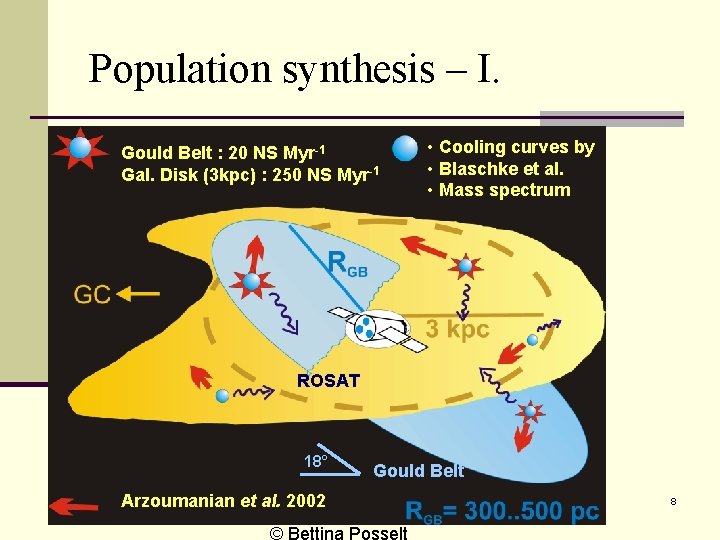
Population synthesis – I. Gould Belt : 20 NS Myr-1 Gal. Disk (3 kpc) : 250 NS Myr-1 • Cooling curves by • Blaschke et al. • Mass spectrum ROSAT 18° Gould Belt Arzoumanian et al. 2002 © Bettina Posselt 8

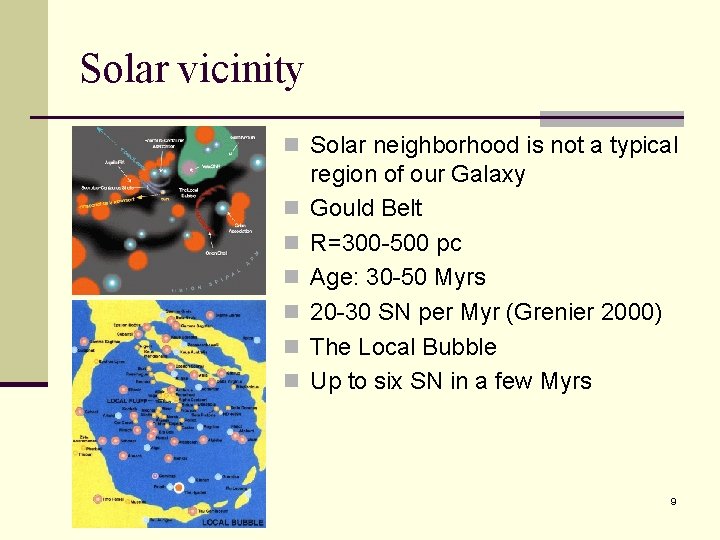
Solar vicinity n Solar neighborhood is not a typical n n n region of our Galaxy Gould Belt R=300 -500 pc Age: 30 -50 Myrs 20 -30 SN per Myr (Grenier 2000) The Local Bubble Up to six SN in a few Myrs 9

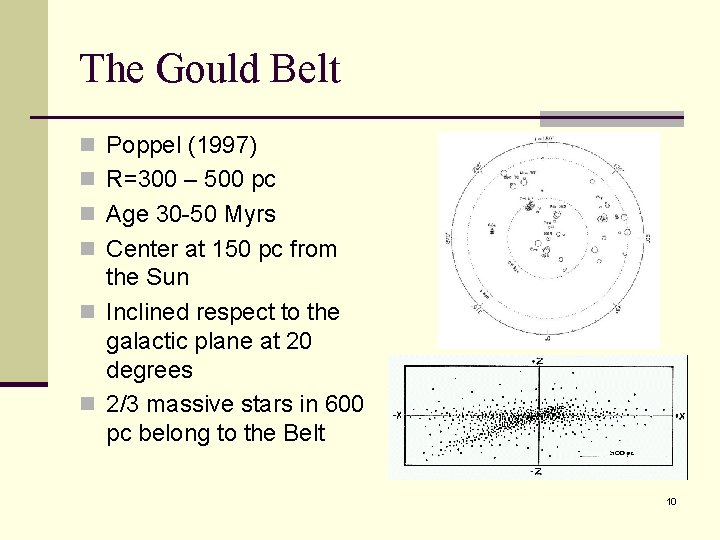
The Gould Belt n Poppel (1997) n R=300 – 500 pc n Age 30 -50 Myrs n Center at 150 pc from the Sun n Inclined respect to the galactic plane at 20 degrees n 2/3 massive stars in 600 pc belong to the Belt 10

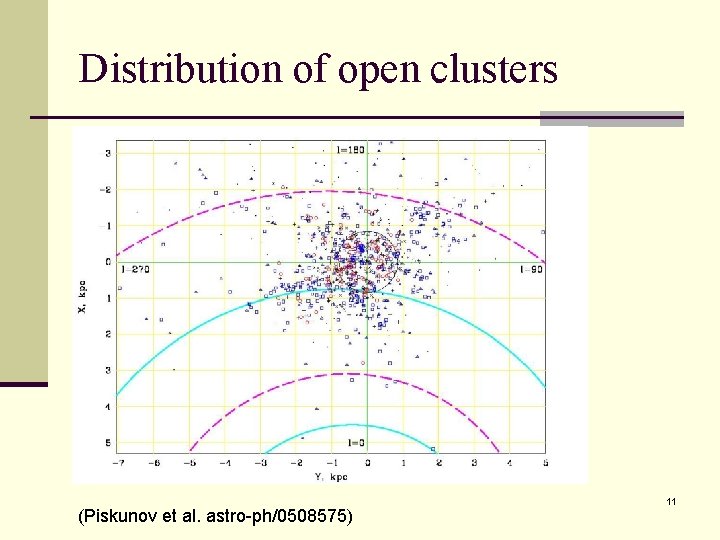
Distribution of open clusters (Piskunov et al. astro-ph/0508575) 11

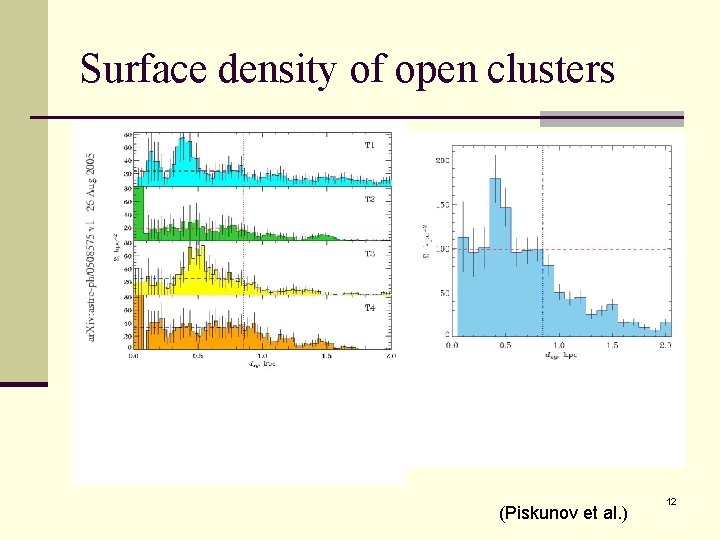
Surface density of open clusters (Piskunov et al. ) 12

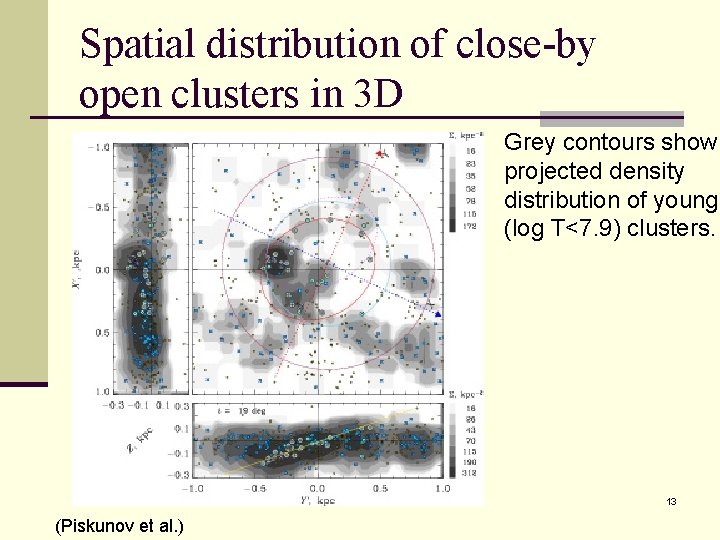
Spatial distribution of close-by open clusters in 3 D Grey contours show projected density distribution of young (log T<7. 9) clusters. 13 (Piskunov et al. )

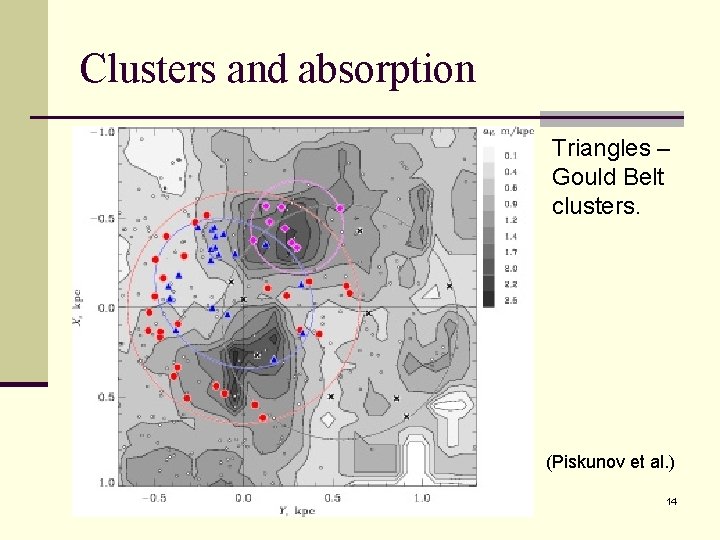
Clusters and absorption Triangles – Gould Belt clusters. (Piskunov et al. ) 14

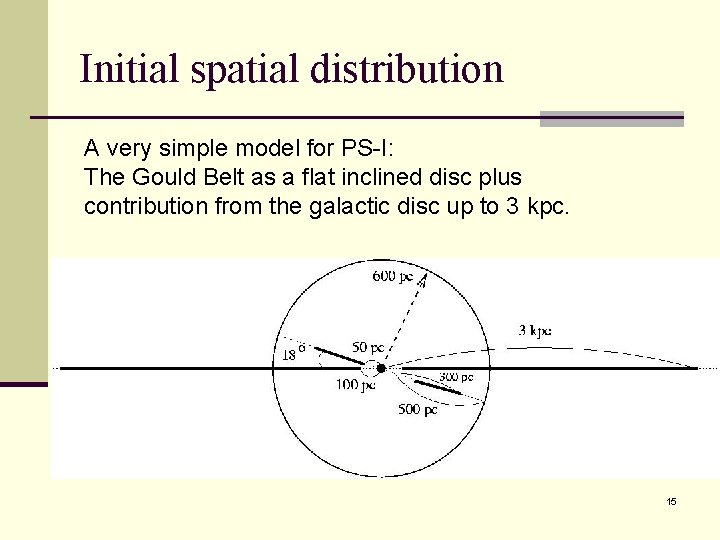
Initial spatial distribution A very simple model for PS-I: The Gould Belt as a flat inclined disc plus contribution from the galactic disc up to 3 kpc. 15

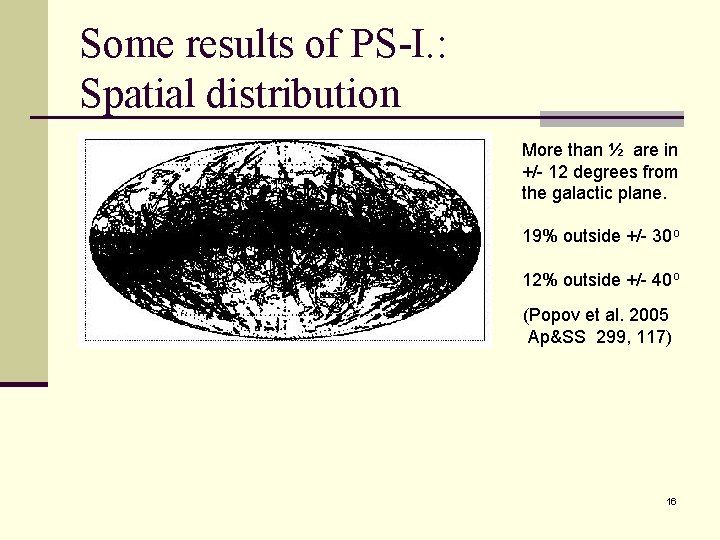
Some results of PS-I. : Spatial distribution More than ½ are in +/- 12 degrees from the galactic plane. 19% outside +/- 30 o 12% outside +/- 40 o (Popov et al. 2005 Ap&SS 299, 117) 16

Mass spectrum of NSs n Mass spectrum of local young NSs can be different from the general one (in the Galaxy) n Hipparcos data on near-by massive stars n Progenitor vs NS mass: Timmes et al. (1996); Woosley et al. (2002) (masses of secondary objects in NS+NS) astro-ph/0305599 17

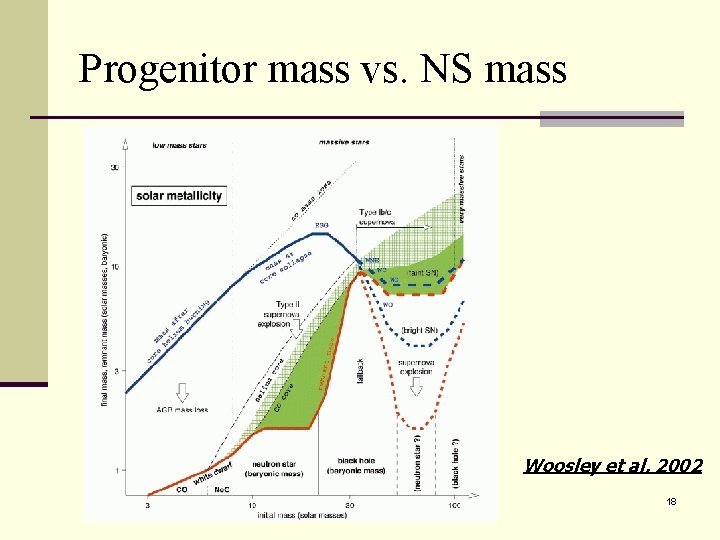
Progenitor mass vs. NS mass Woosley et al. 2002 18

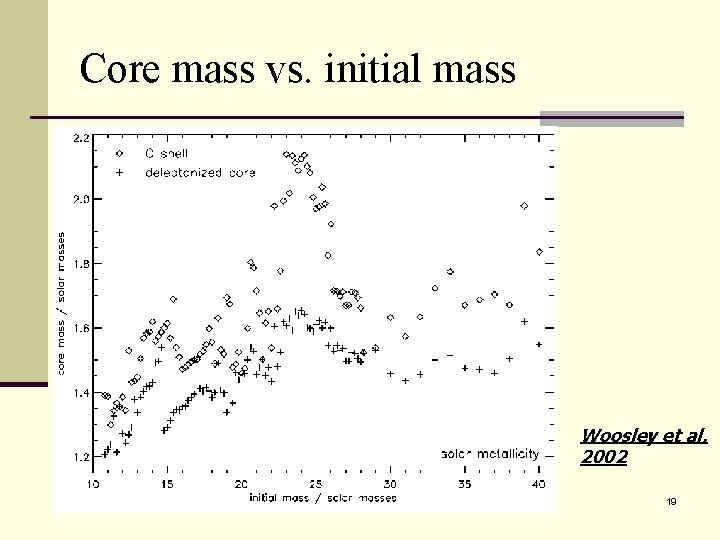
Core mass vs. initial mass Woosley et al. 2002 19

Two tests Age – Temperature & Log N – Log S 20

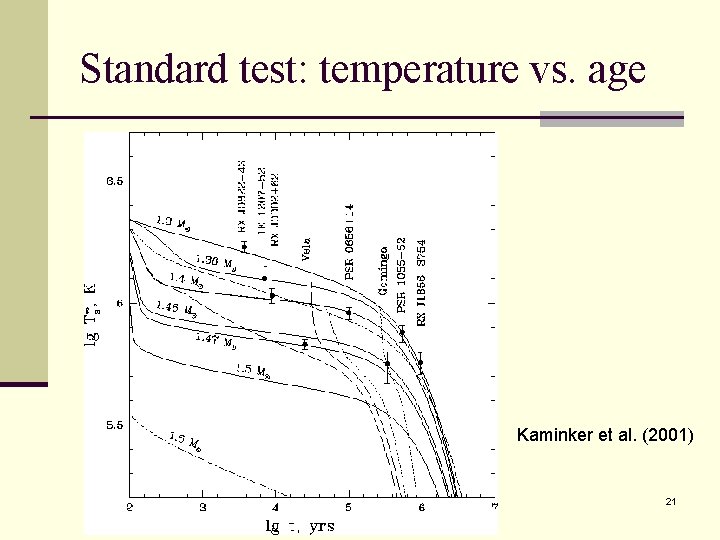
Standard test: temperature vs. age Kaminker et al. (2001) 21

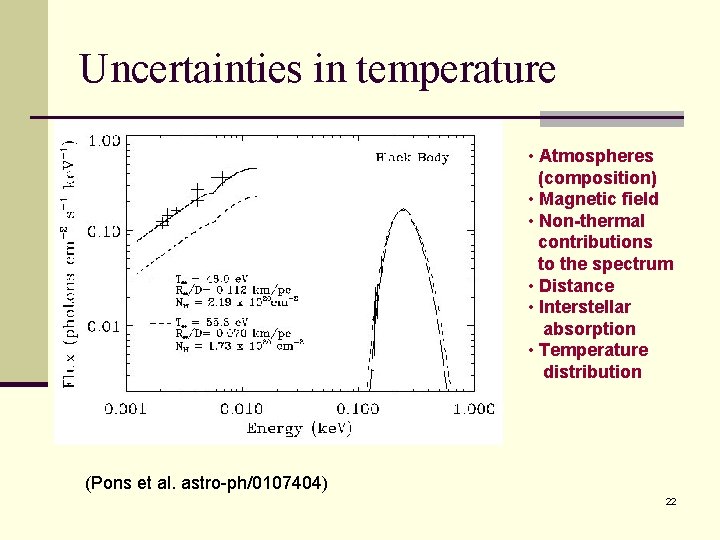
Uncertainties in temperature • Atmospheres (composition) • Magnetic field • Non-thermal contributions to the spectrum • Distance • Interstellar absorption • Temperature distribution (Pons et al. astro-ph/0107404) 22

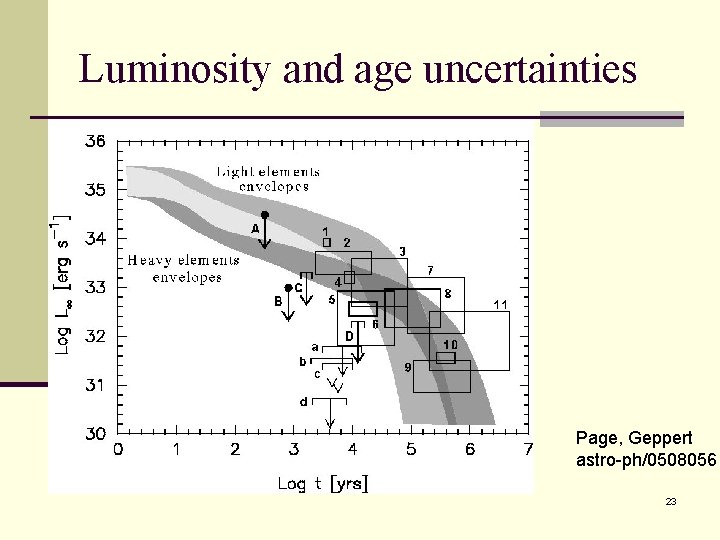
Luminosity and age uncertainties Page, Geppert astro-ph/0508056 23

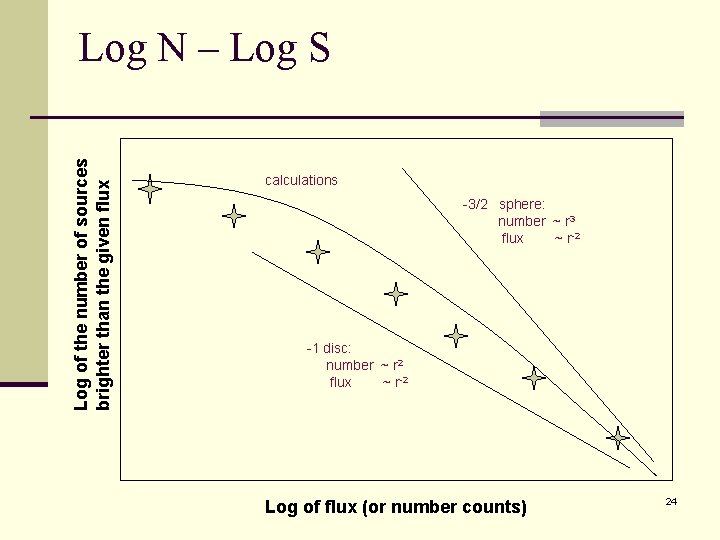
Log of the number of sources brighter than the given flux Log N – Log S calculations -3/2 sphere: number ~ r 3 flux ~ r-2 -1 disc: number ~ r 2 flux ~ r-2 Log of flux (or number counts) 24

Log N – Log S as an additional test n Standard test: Age – Temperature n Sensitive to ages <105 years n Uncertain age and temperature n Non-uniform sample n Log N – Log S n Sensitive to ages >105 years (when applied to close-by NSs) n Definite N (number) and S (flux) n Uniform sample n Two test are perfect together!!! astro-ph/0411618 25

List of models (Blaschke et al. 2004) Blaschke et al. used 16 sets of cooling curves. They were different in three main respects: 1. Absence or presence of pion condensate 2. Different gaps for superfluid protons and neutrons 3. Different Ts-Tin Pions Crust n Model I. n n n n Yes Model II. No Model III. Yes Model IV. No Model V. Yes Model VI. No Model VII. Yes Model VIII. Yes Model IX. No C D C C D E C C C Gaps A B B B’ B’’ A 26

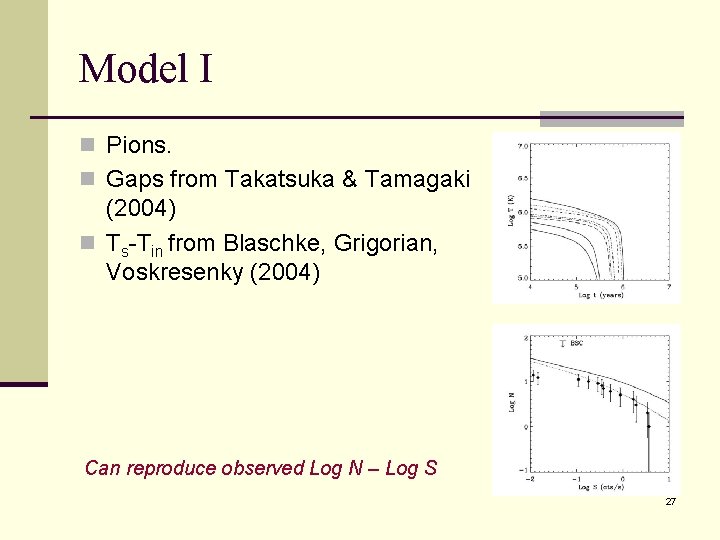
Model I n Pions. n Gaps from Takatsuka & Tamagaki (2004) n Ts-Tin from Blaschke, Grigorian, Voskresenky (2004) Can reproduce observed Log N – Log S 27

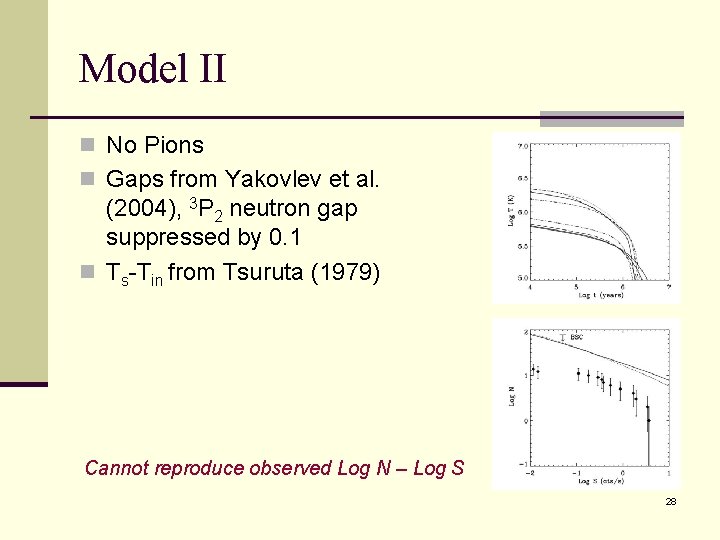
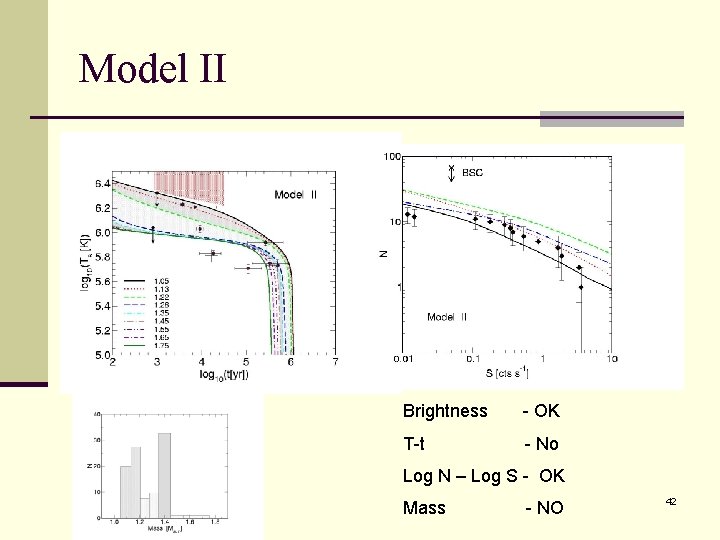
Model II n No Pions n Gaps from Yakovlev et al. (2004), 3 P 2 neutron gap suppressed by 0. 1 n Ts-Tin from Tsuruta (1979) Cannot reproduce observed Log N – Log S 28

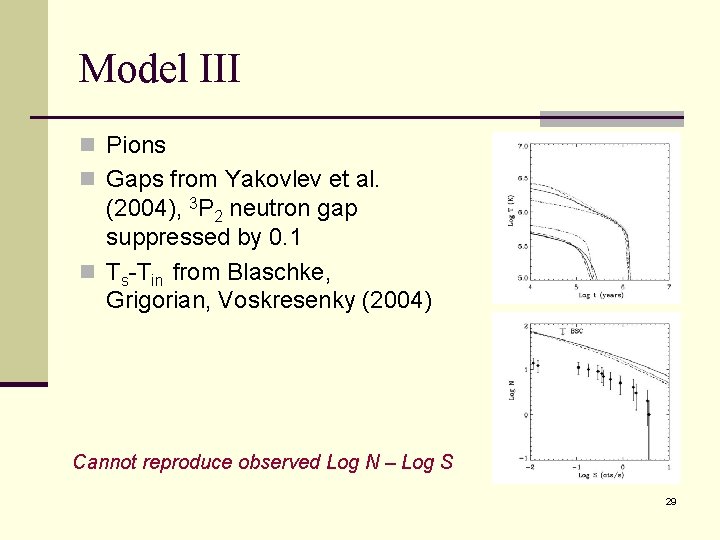
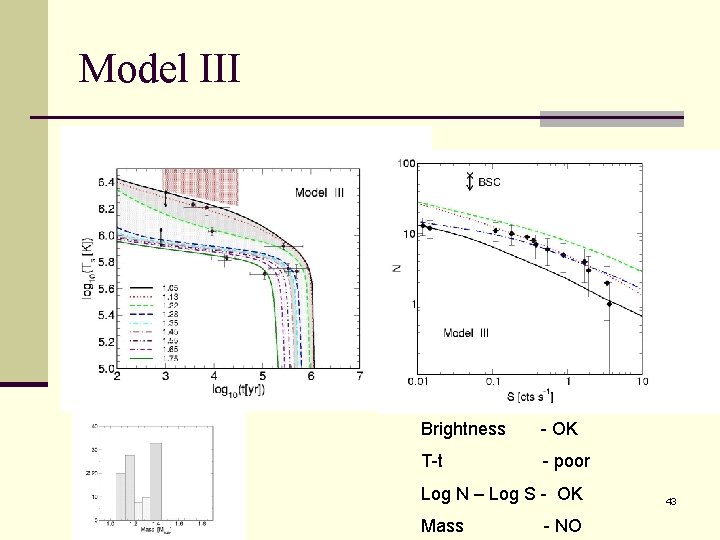
Model III n Pions n Gaps from Yakovlev et al. (2004), 3 P 2 neutron gap suppressed by 0. 1 n Ts-Tin from Blaschke, Grigorian, Voskresenky (2004) Cannot reproduce observed Log N – Log S 29

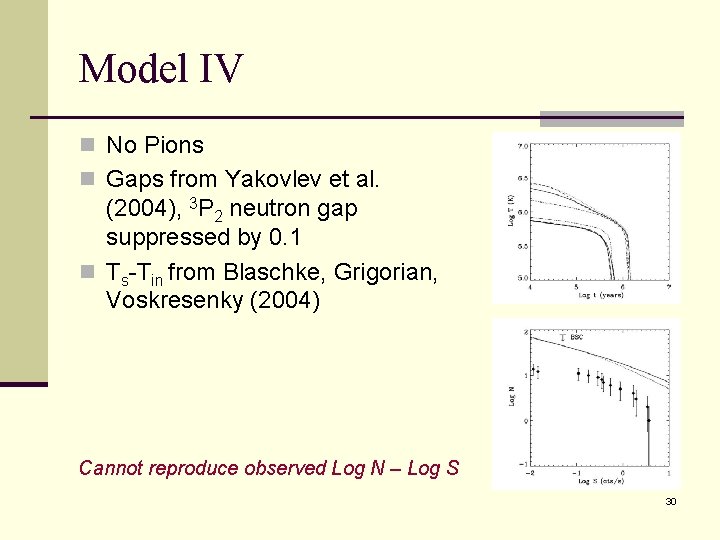
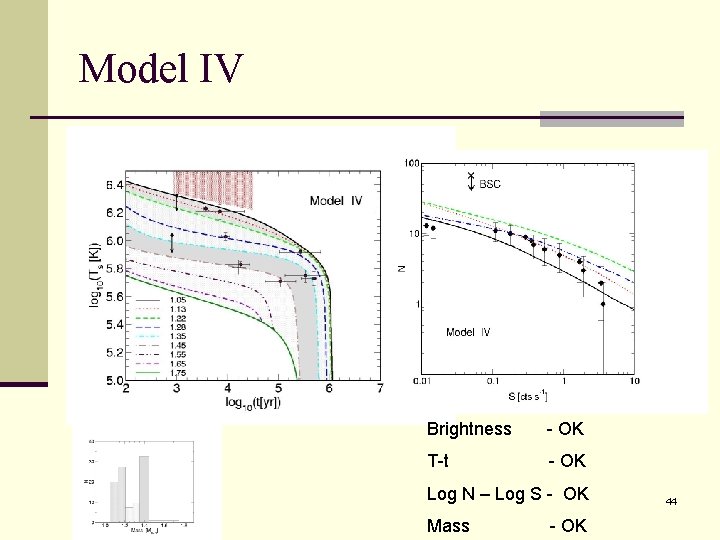
Model IV n No Pions n Gaps from Yakovlev et al. (2004), 3 P 2 neutron gap suppressed by 0. 1 n Ts-Tin from Blaschke, Grigorian, Voskresenky (2004) Cannot reproduce observed Log N – Log S 30

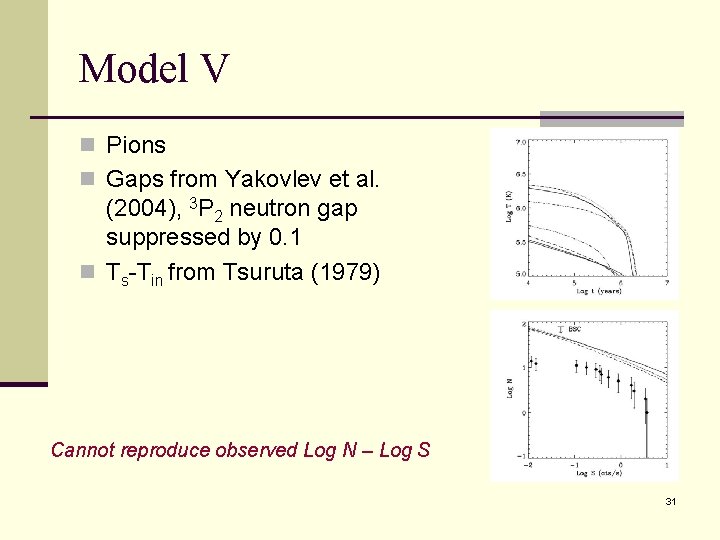
Model V n Pions n Gaps from Yakovlev et al. (2004), 3 P 2 neutron gap suppressed by 0. 1 n Ts-Tin from Tsuruta (1979) Cannot reproduce observed Log N – Log S 31

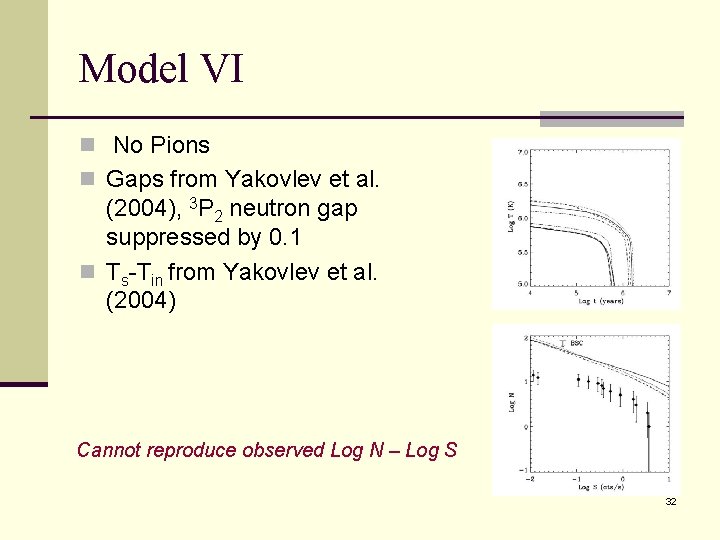
Model VI n No Pions n Gaps from Yakovlev et al. (2004), 3 P 2 neutron gap suppressed by 0. 1 n Ts-Tin from Yakovlev et al. (2004) Cannot reproduce observed Log N – Log S 32

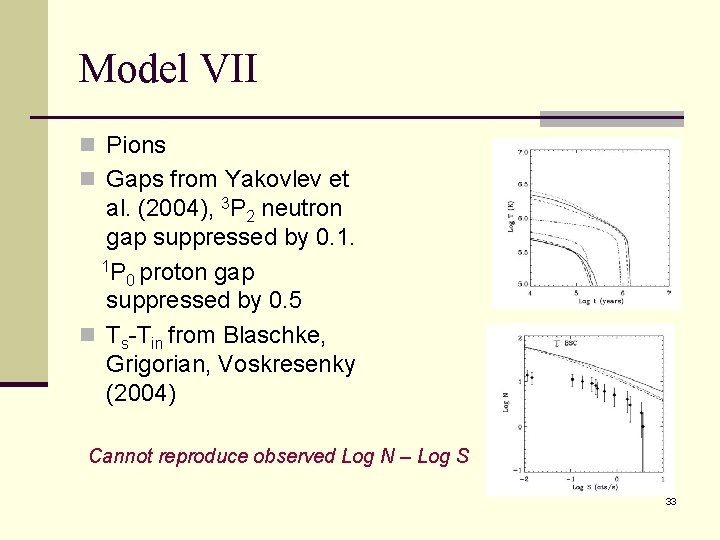
Model VII n Pions n Gaps from Yakovlev et al. (2004), 3 P 2 neutron gap suppressed by 0. 1. 1 P proton gap 0 suppressed by 0. 5 n Ts-Tin from Blaschke, Grigorian, Voskresenky (2004) Cannot reproduce observed Log N – Log S 33

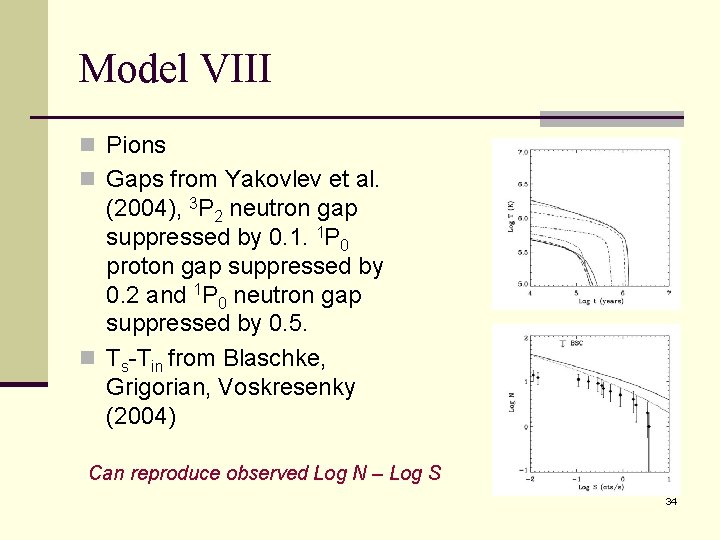
Model VIII n Pions n Gaps from Yakovlev et al. (2004), 3 P 2 neutron gap suppressed by 0. 1. 1 P 0 proton gap suppressed by 0. 2 and 1 P 0 neutron gap suppressed by 0. 5. n Ts-Tin from Blaschke, Grigorian, Voskresenky (2004) Can reproduce observed Log N – Log S 34

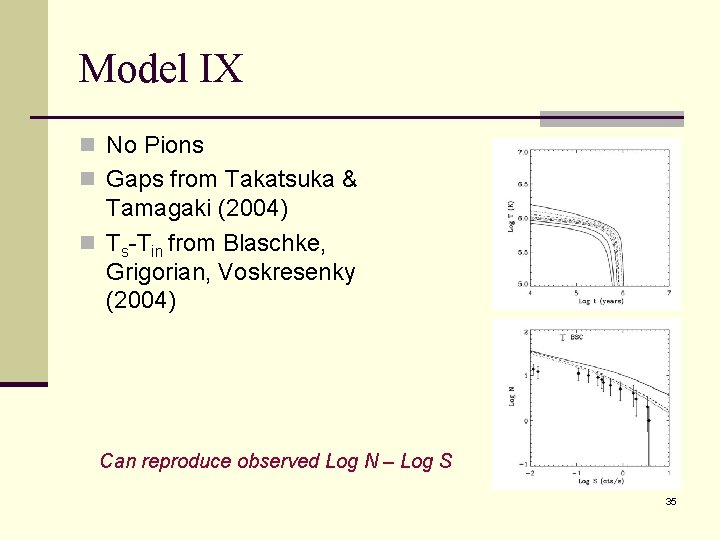
Model IX n No Pions n Gaps from Takatsuka & Tamagaki (2004) n Ts-Tin from Blaschke, Grigorian, Voskresenky (2004) Can reproduce observed Log N – Log S 35

HOORAY!!!! Log N – Log S can select models!!!!! Only three (or even one!) passed the second test! ……. still………… is it possible just to update the temperature-age test? ? ? May be Log N – Log S is not necessary? Let’s try!!!! 36

Brightness constraint n Effects of the crust (envelope) n Fitting the crust it is possible to fulfill the T-t test … n …but not the second test: Log N – Log S !!! (H. Grigorian astro-ph/0507052) 37

Sensitivity of Log N – Log S n Log N – Log S is very sensitive to gaps n Log N – Log S is not sensitive to the crust if it is applied to relatively old objects (>104 -5 yrs) n Log N – Log S is not very sensitive to presence or absence of pions We conclude that the two test complement each other 38

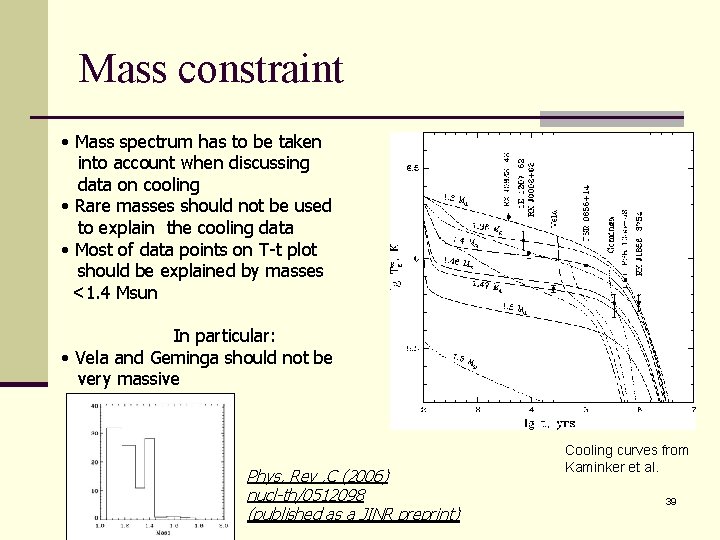
Mass constraint • Mass spectrum has to be taken into account when discussing data on cooling • Rare masses should not be used to explain the cooling data • Most of data points on T-t plot should be explained by masses <1. 4 Msun In particular: • Vela and Geminga should not be very massive Phys. Rev. C (2006) nucl-th/0512098 (published as a JINR preprint) Cooling curves from Kaminker et al. 39

Another attempt to test a set of models: hybrid stars We studied several models for hybrid stars applying all possible tests: - T-t - Log N – Log S - Brightness constraint - Mass constraint We also tried to present examples when a model successfully passes the Log N – Log S test, but fails to pass the standard T-t test or fails to fulfill the mass constraint. nucl-th/0512098 40

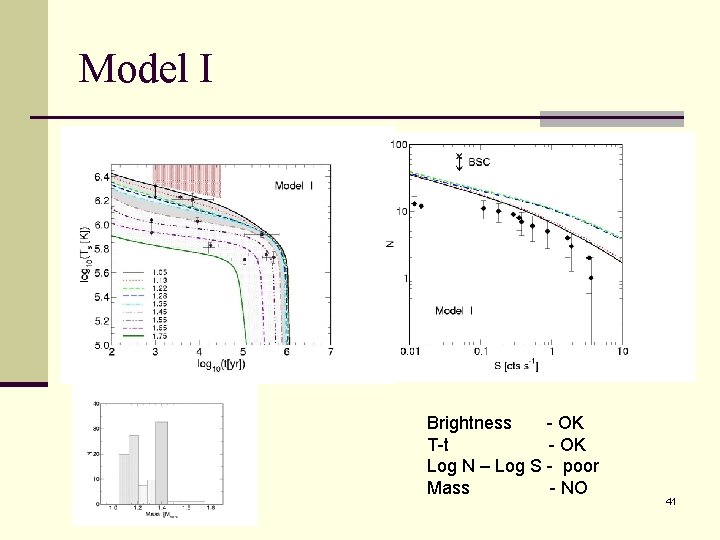
Model I Brightness - OK T-t - OK Log N – Log S - poor Mass - NO 41

Model II Brightness - OK T-t - No Log N – Log S - OK Mass - NO 42

Model III Brightness - OK T-t - poor Log N – Log S - OK Mass - NO 43

Model IV Brightness - OK T-t - OK Log N – Log S - OK Mass - OK 44

Resume for Hy. Ss One model among four was able to pass all tests. 45

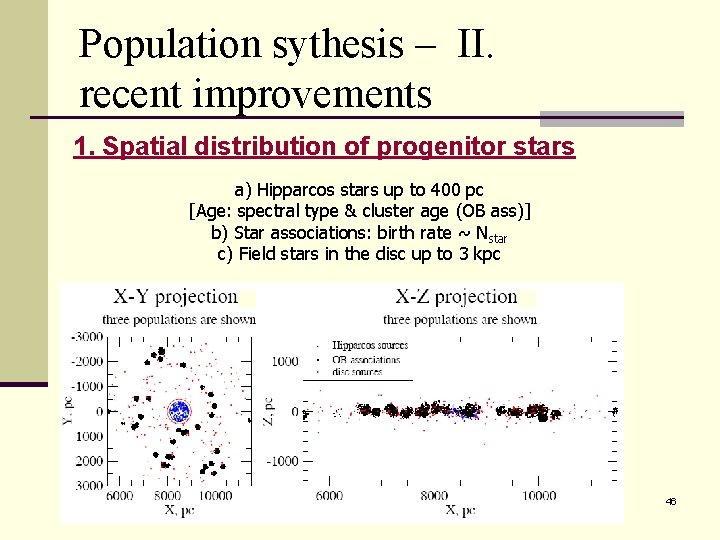
Population sythesis – II. recent improvements 1. Spatial distribution of progenitor stars a) Hipparcos stars up to 400 pc [Age: spectral type & cluster age (OB ass)] b) Star associations: birth rate ~ Nstar c) Field stars in the disc up to 3 kpc 46

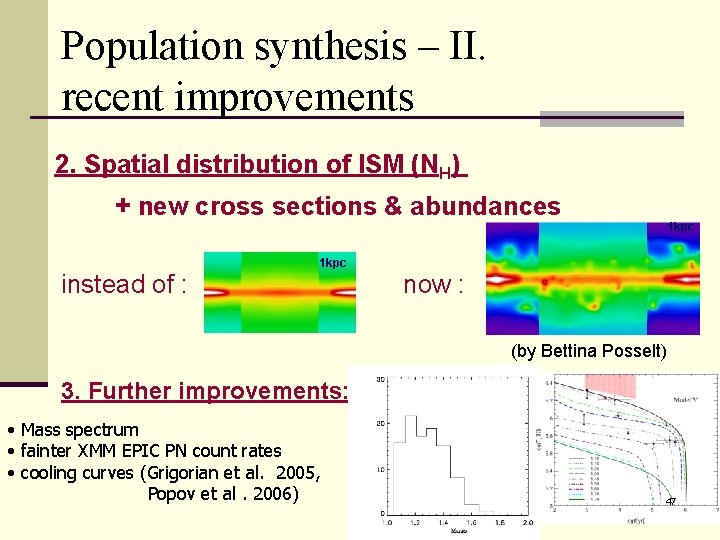
Population synthesis – II. recent improvements 2. Spatial distribution of ISM (NH) + new cross sections & abundances 1 kpc instead of : 1 kpc now : (by Bettina Posselt) 3. Further improvements: • Mass spectrum • fainter XMM EPIC PN count rates • cooling curves (Grigorian et al. 2005, Popov et al. 2006) 47

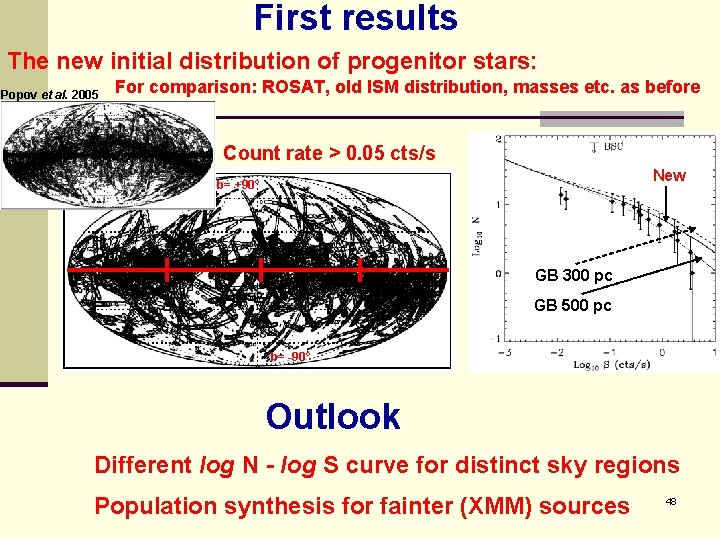
First results The new initial distribution of progenitor stars: Popov et al. 2005 For comparison: ROSAT, old ISM distribution, masses etc. as before Count rate > 0. 05 cts/s New b= +90° GB 300 pc GB 500 pc b= -90° Outlook Different log N - log S curve for distinct sky regions Population synthesis for fainter (XMM) sources 48

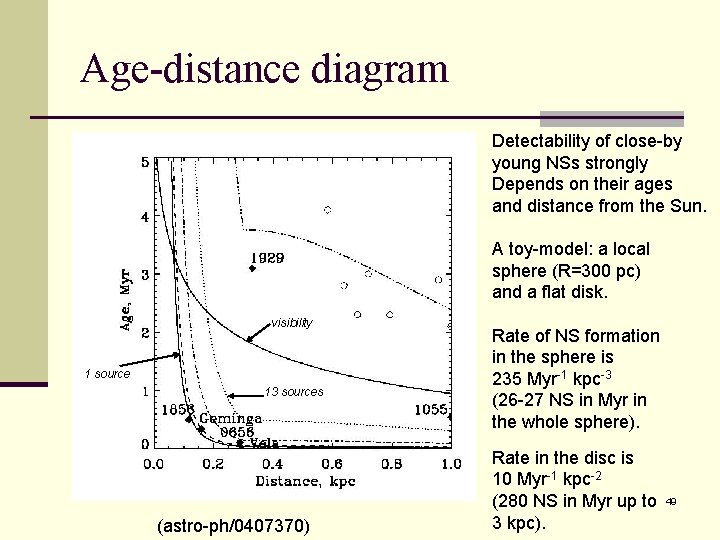
Age-distance diagram Detectability of close-by young NSs strongly Depends on their ages and distance from the Sun. A toy-model: a local sphere (R=300 pc) and a flat disk. visibility 1 source 13 sources (astro-ph/0407370) Rate of NS formation in the sphere is 235 Myr-1 kpc-3 (26 -27 NS in Myr in the whole sphere). Rate in the disc is 10 Myr-1 kpc-2 (280 NS in Myr up to 3 kpc). 49

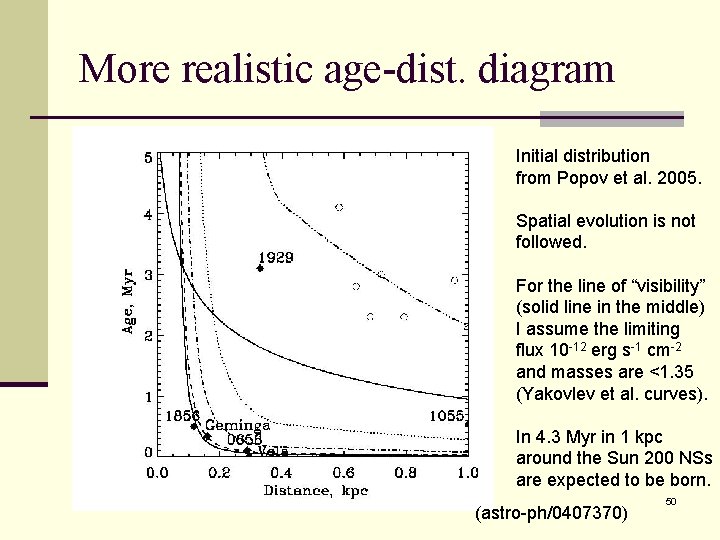
More realistic age-dist. diagram Initial distribution from Popov et al. 2005. Spatial evolution is not followed. For the line of “visibility” (solid line in the middle) I assume the limiting flux 10 -12 erg s-1 cm-2 and masses are <1. 35 (Yakovlev et al. curves). In 4. 3 Myr in 1 kpc around the Sun 200 NSs are expected to be born. (astro-ph/0407370) 50

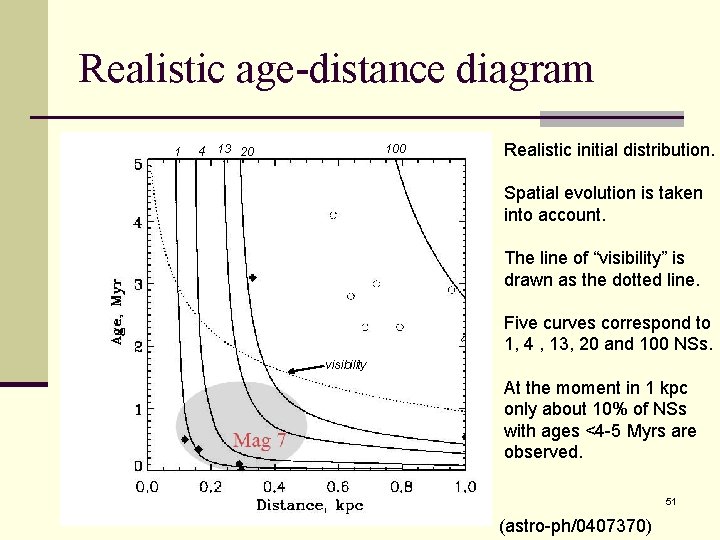
Realistic age-distance diagram 1 4 13 20 100 Realistic initial distribution. Spatial evolution is taken into account. The line of “visibility” is drawn as the dotted line. Five curves correspond to 1, 4 , 13, 20 and 100 NSs. visibility At the moment in 1 kpc only about 10% of NSs with ages <4 -5 Myrs are observed. 51 (astro-ph/0407370)

Resume n We live in a very interesting region of the Milky Way! n Log N – Log S test can include NSs with n n unknown ages, so additional sources (like the Magnificent Seven) can be used to test cooling curves. Two tests (Log. N–Log. S and Age-Temperature) are perfect together. Additional considerations (brightness and mass constraints) have to be taken into account. More detailed PS models are welcomed. Age-distance diagram can be used as an additional tool. 52

THAT’S ALL. THANK YOU! 53

Radio detection Malofeev et al. (2005) reported detection of 1 RXS J 1308. 6+212708 (RBS 1223) in the low-frequency band (60 -110 MHz) with the radio telescope in Pushchino. In 2006 Malofeev et al. reported radio detection of another one. (back) 54

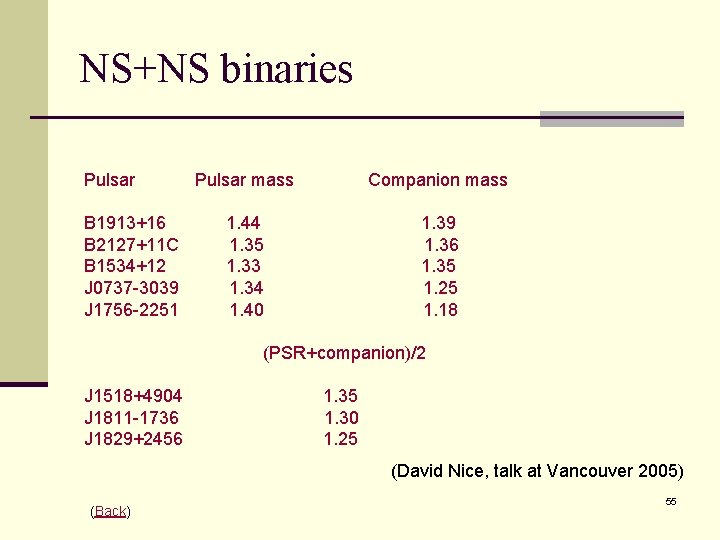
NS+NS binaries Pulsar B 1913+16 B 2127+11 C B 1534+12 J 0737 -3039 J 1756 -2251 Pulsar mass Companion mass 1. 44 1. 35 1. 33 1. 34 1. 40 1. 39 1. 36 1. 35 1. 25 1. 18 (PSR+companion)/2 J 1518+4904 J 1811 -1736 J 1829+2456 1. 35 1. 30 1. 25 (David Nice, talk at Vancouver 2005) (Back) 55