Population Balance Techniques in Chemical Engineering by Richard

Population Balance Techniques in Chemical Engineering by Richard Gilbert & Nihat M. Gürmen September 29, 1999 Department of Chemical Engineering University of South Florida Tampa, USA R. Gilbert & N. Gürmen, v. 1. 0, Tampa 1999

Part I -- Overview R. Gilbert & N. Gürmen, v. 1. 0, Tampa 1999

What is the Population Balance Technique (PBT)? PBT is a mathematical framework for an accounting procedure for particles of certain types you are interested in. The technique is very useful where identity of individual particles is modified or destroyed by coalescence or breakage. R. Gilbert & N. Gürmen, v. 1. 0, Tampa 1999

(Dis)advantage of PBT Advantage • Analysis of complex dispersed phase system Disadvantage • Difficult integro-partial differential equations R. Gilbert & N. Gürmen, v. 1. 0, Tampa 1999

Application Areas • colloidal systems • crystallization • fluidization • microbial growths • demographic analysis R. Gilbert & N. Gürmen, v. 1. 0, Tampa 1999

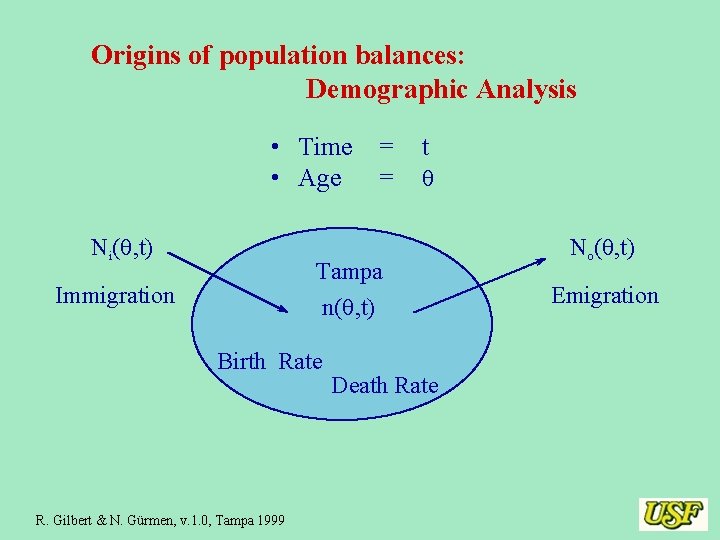
Origins of population balances: Demographic Analysis • Time = • Age = Ni(q, t) t q Tampa n(q, t) Immigration Birth Rate R. Gilbert & N. Gürmen, v. 1. 0, Tampa 1999 Death Rate No(q, t) Emigration

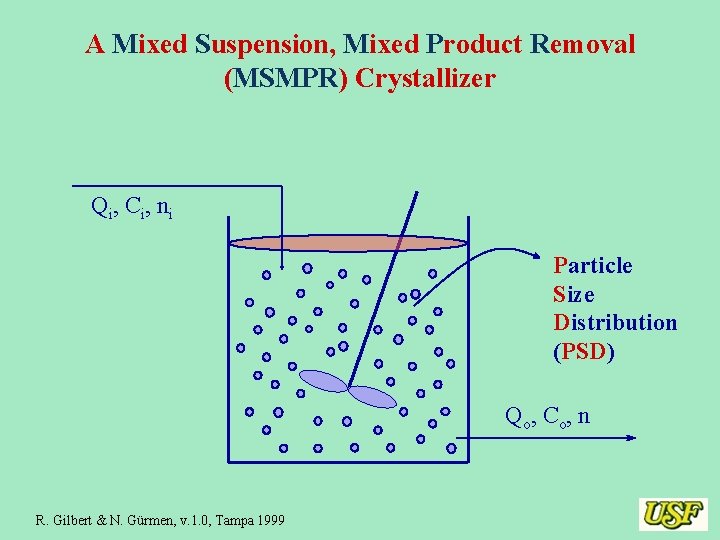
A Mixed Suspension, Mixed Product Removal (MSMPR) Crystallizer Qi, Ci, ni Particle Size Distribution (PSD) Qo, Co, n R. Gilbert & N. Gürmen, v. 1. 0, Tampa 1999

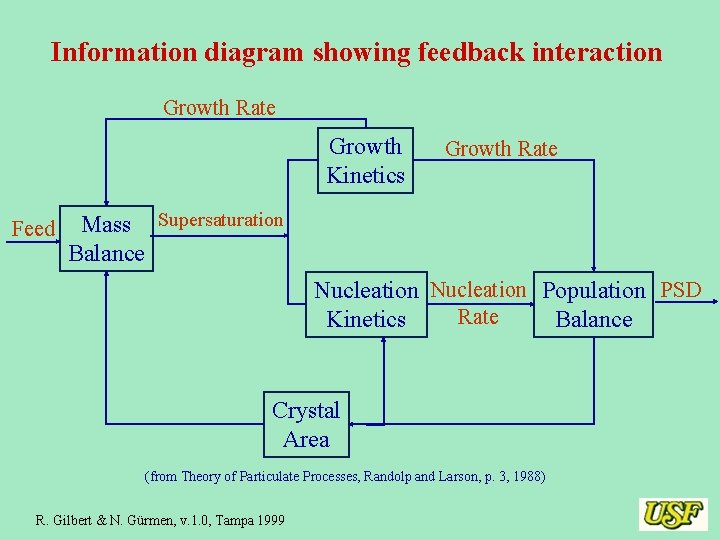
Information diagram showing feedback interaction Growth Rate Growth Kinetics Feed Growth Rate Mass Supersaturation Balance Nucleation Population PSD Rate Kinetics Balance Crystal Area (from Theory of Particulate Processes, Randolp and Larson, p. 3, 1988) R. Gilbert & N. Gürmen, v. 1. 0, Tampa 1999

Part II -- Mathematical Background R. Gilbert & N. Gürmen, v. 1. 0, Tampa 1999

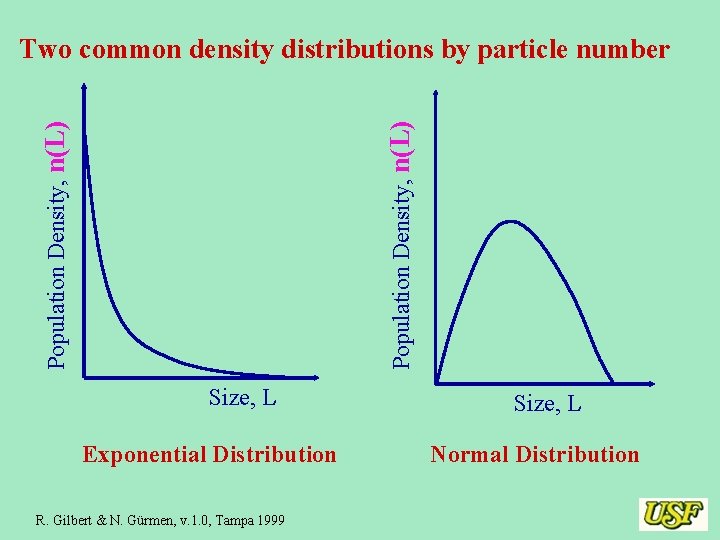
Population Density, n(L) Two common density distributions by particle number Size, L Exponential Distribution R. Gilbert & N. Gürmen, v. 1. 0, Tampa 1999 Size, L Normal Distribution

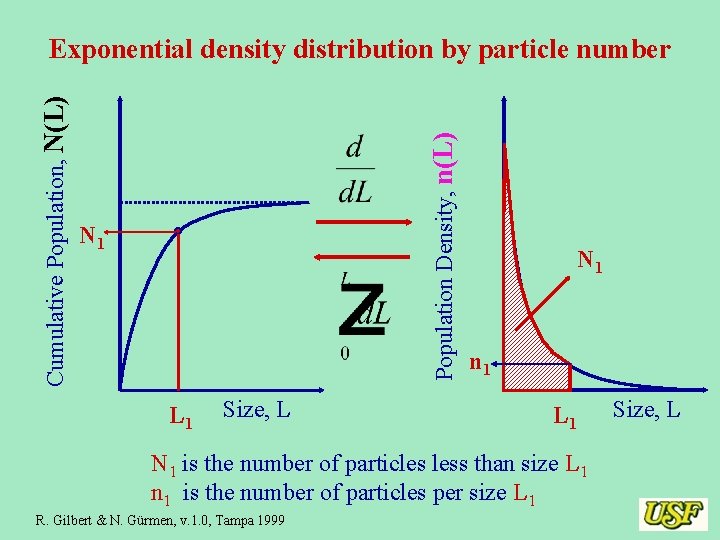
Population Density, n(L) Cumulative Population, N(L) Exponential density distribution by particle number N 1 L 1 Size, L N 1 n 1 L 1 N 1 is the number of particles less than size L 1 n 1 is the number of particles per size L 1 R. Gilbert & N. Gürmen, v. 1. 0, Tampa 1999 Size, L

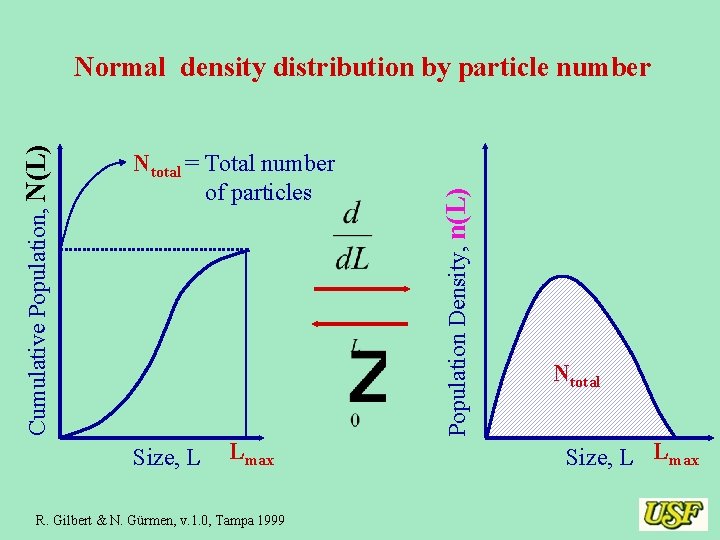
Ntotal = Total number of particles Size, L Lmax R. Gilbert & N. Gürmen, v. 1. 0, Tampa 1999 Population Density, n(L) Cumulative Population, N(L) Normal density distribution by particle number Ntotal Size, L Lmax

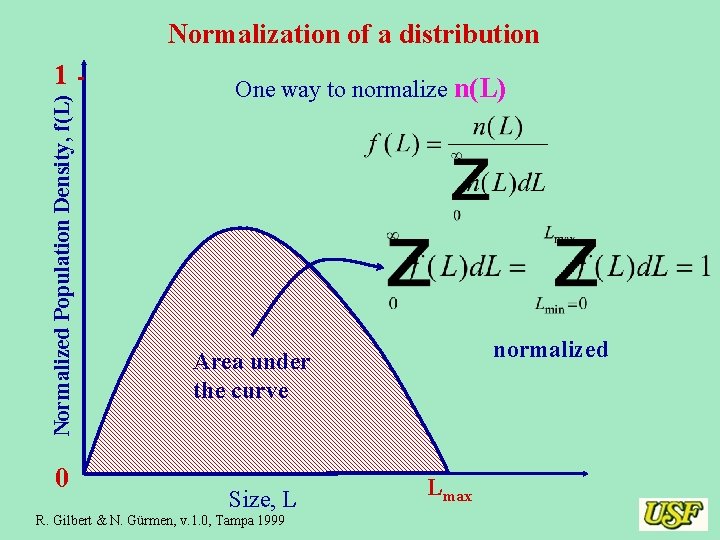
Normalization of a distribution Normalized Population Density, f(L) 1 0 One way to normalize n(L) normalized Area under the curve Size, L R. Gilbert & N. Gürmen, v. 1. 0, Tampa 1999 Lmax

Average properties of a distribution The two important parameters of a particle size distribution are * How large are the particles? mean size, * How much variation do they have with respect to the mean size? coefficient of variation, c. v. where 2 (variance) is R. Gilbert & N. Gürmen, v. 1. 0, Tampa 1999

Moments of a distribution j-th moment, mj, of a distribution f(L) about L 1 Mean, = the first moment about zero Variance, 2 = the second moment about the mean R. Gilbert & N. Gürmen, v. 1. 0, Tampa 1999

Further average properties: Skewness and Kurtosis j-th moment, j, of a distribution f(L) about mean Skewness, 1 = measure of the symmetry about the mean (zero for symmetric distributions) Kurtosis, 2 = measure of the shape of tails of a distribution R. Gilbert & N. Gürmen, v. 1. 0, Tampa 1999

Part III -- Formulation of Population Balance Technique R. Gilbert & N. Gürmen, v. 1. 0, Tampa 1999

Basic Assumptions of PBT (Population Balance Technique) • Particles are numerous enough to approximate a continuum • Each particle has identical trajectory in particle phase space S spanned by the chosen independent variables • Systems can be micro- or macrodistributed Check these Assumptions R. Gilbert & N. Gürmen, v. 1. 0, Tampa 1999

Basic Definitions Number density function n(S, t) is defined in an (m+3)-dimensional space S consisted of 3 external (spatial) coordinates m internal coordinates (size, age, etc. ) Total number of particles is given by Space S R. Gilbert & N. Gürmen, v. 1. 0, Tampa 1999

The particle number continuity equation R 1 S R. Gilbert & N. Gürmen, v. 1. 0, Tampa 1999 a subregion R 1 from the Lagrangian viewpoint

Convenient variable and operator definitions is the set of internal and external coordinates spanning the phase space R 1 R. Gilbert & N. Gürmen, v. 1. 0, Tampa 1999 where

Applying the product rule of differentiation to the LHS R. Gilbert & N. Gürmen, v. 1. 0, Tampa 1999

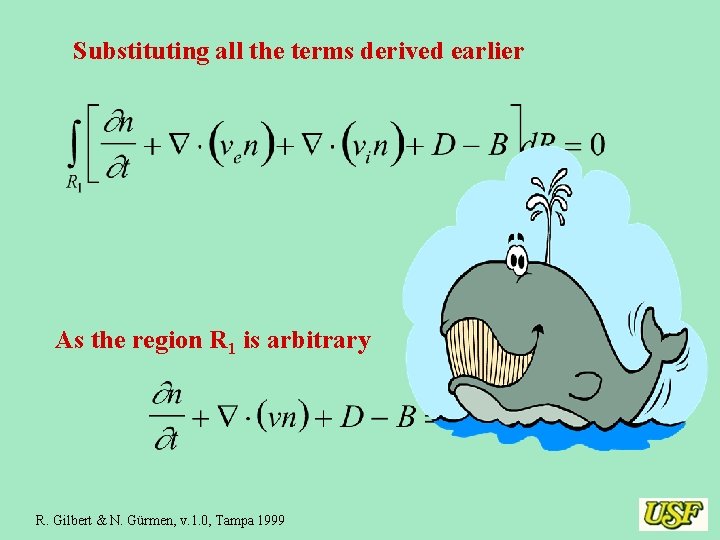
Substituting all the terms derived earlier As the region R 1 is arbitrary R. Gilbert & N. Gürmen, v. 1. 0, Tampa 1999

In terms of m+3 coordinates Micro-distributed Population Balance Equation Averaging the equation in the external coordinates Macro-distributed Population Balance Equation R. Gilbert & N. Gürmen, v. 1. 0, Tampa 1999

B - D terms represent the rate of coalescence conventionally collision integrals are used for B and D the rate at which a bubble of volume u coalesces with a bubble of volume v-u to make a new bubble of volume v is a death function consistent with the above birth function would be R. Gilbert & N. Gürmen, v. 1. 0, Tampa 1999

Coagulation kernel, C(x, y) : the rate at which bubbles of volumes x and y collide and coalesce. in the modeling of aerosols two of the functions used for C(x, y) are where Ka is the coalescence rate constant 1) Brownian motion 2) Shear flow R. Gilbert & N. Gürmen, v. 1. 0, Tampa 1999

Simplifications for a Solvable System • dynamic system => t • spatially distributed => x, y, z • single internal variable, size => L Growth rate G is at most linearly dependent with particle size => R. Gilbert & N. Gürmen, v. 1. 0, Tampa 1999

Moment Transformation Defining the jth moment of the number density function as Averaging PB in in the L dimension R. Gilbert & N. Gürmen, v. 1. 0, Tampa 1999

Microdistributed form of moment transformation j = 0, 1, 2, . . . ³ k Macrodistributed form of moment transformation j = 0, 1, 2, . . . ³ k R. Gilbert & N. Gürmen, v. 1. 0, Tampa 1999

If Assumptions Do Not Allow Moment Transformations You have to use other methods of solving PDEs like • method of lines • finite element methods difficult if both of your variables go to infinity R. Gilbert & N. Gürmen, v. 1. 0, Tampa 1999

Part IV -- Examples R. Gilbert & N. Gürmen, v. 1. 0, Tampa 1999

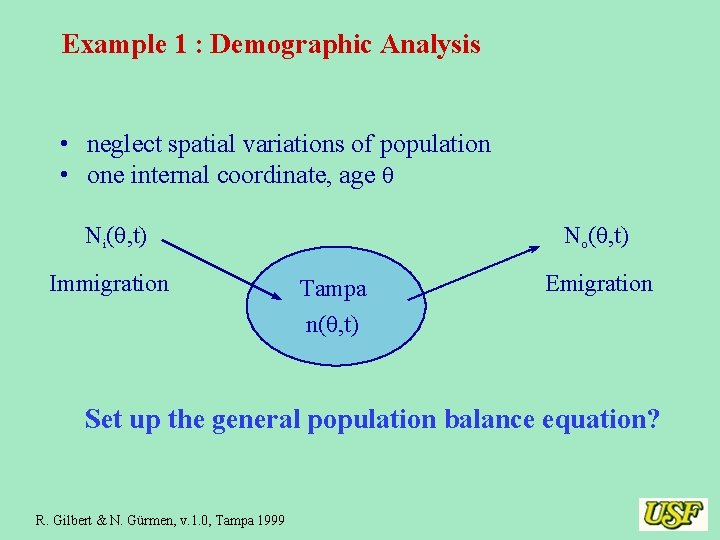
Example 1 : Demographic Analysis • neglect spatial variations of population • one internal coordinate, age q Ni(q, t) Immigration No(q, t) Tampa n(q, t) Emigration Set up the general population balance equation? R. Gilbert & N. Gürmen, v. 1. 0, Tampa 1999

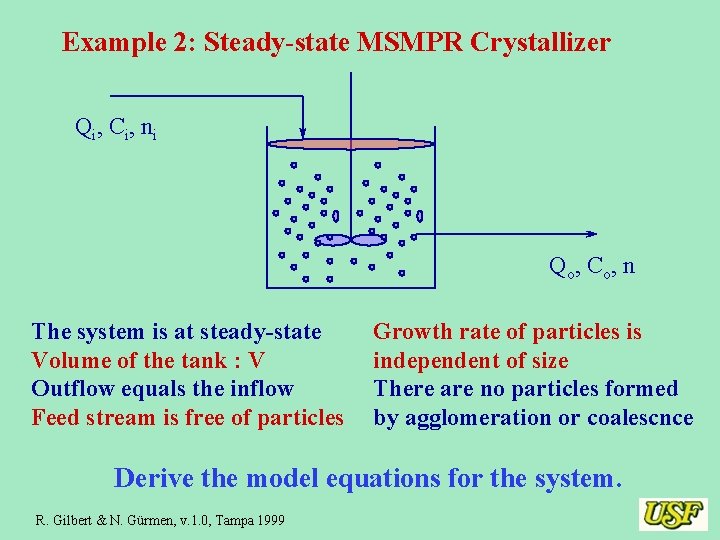
Example 2: Steady-state MSMPR Crystallizer Qi, Ci, ni Qo, Co, n The system is at steady-state Volume of the tank : V Outflow equals the inflow Feed stream is free of particles Growth rate of particles is independent of size There are no particles formed by agglomeration or coalescnce Derive the model equations for the system. R. Gilbert & N. Gürmen, v. 1. 0, Tampa 1999

References BOOK • Randolph A. D. and M. A. Larson, Theory of Particulate Processes, 2 nd edition, 1988, Academic Press PAPERS • Hounslow M. J. , R. L. Ryall, and V. R. Marhsall, A discretized population balance for nucleation, growth, and aggregation, AICh. E Journal, 34: 11, p. 1821 -1832, 1988 • Hulburt H. M. and T. Akiyama, Liouville equations for agglomeration and dispersion processes, I&EC Fundamentals, 8: 2, p. 319 -324, 1969 • Ramkrishna D. , The prospects of population balances, Chemical Engineering Education, p. 14 -17, 43, 1978 R. Gilbert & N. Gürmen, v. 1. 0, Tampa 1999

THE END R. Gilbert & N. Gürmen, v. 1. 0, Tampa 1999