Ponavljanje gradiva 7 razreda U 7 razredu smo







































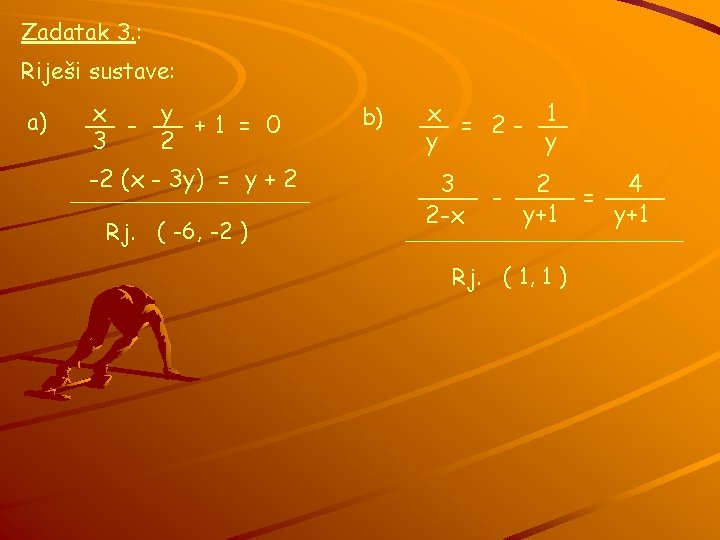














- Slides: 72

Ponavljanje gradiva 7. razreda

U 7. razredu smo učili: - koordinatni sustav u ravnini - o proporcionalnim i obrnuto proporcionalnim veličinama - postotke i jednostavni kamatni račun - statistiku i vjerojatnost - o mnogokutima - o sličnim trokutima - o krugu i kružnici - kako riješiti sustav jednadžbi - o linearnim funkcijama i jednadžbi pravca. Sjećaš li se toga? Ponovimo. . . (Za ponavljanje određenog poglavlja, samo kliknite gore na naziv. )

1. Koordinatni sustav u ravnini

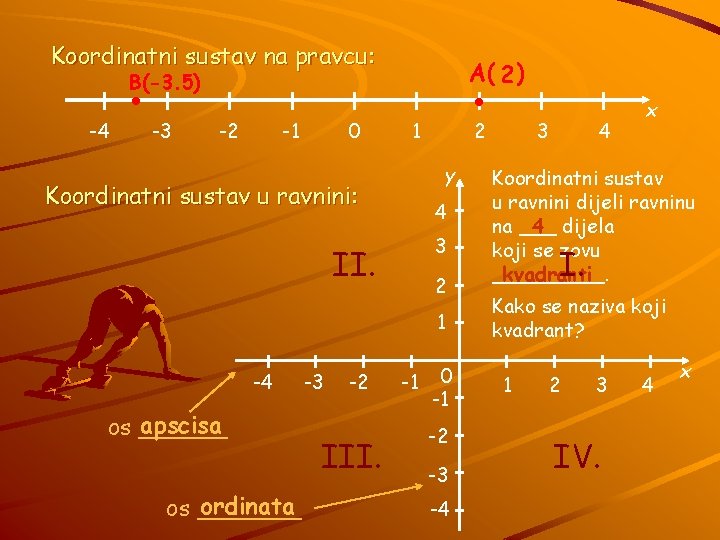
. . Koordinatni sustav na pravcu: jedinična dužina A( 2 ? ) B(-3. 5) -4 -3 -2 0 -1 1 2 3 y Gdje je točka 4 B(-3. 5)? Gdje je točka 3 M(-3, -2. 5)? Koordinatni sustav u ravnini: . C(-4, 2 ? ) 2 1 -4 -3 . -2 4 x -1 0 -1 -2 M(-3, -2. 5) -3 -4 . D( 2, 0 ? ) . 1 2 K( 0, -4 ? ) 3 4 x

. . Koordinatni sustav na pravcu: A( 2 ) B(-3. 5) -4 -3 -2 0 -1 1 2 y Koordinatni sustav u ravnini: 4 3 II. 2 1 -4 apscisa os ______ ordinata os _______ -3 -2 III. -1 0 -1 -2 -3 -4 3 4 x Koordinatni sustav u ravnini dijeli ravninu 4 dijela na ___ koji se zovu kvadranti _____. I. Kako se naziva koji kvadrant? 1 2 3 IV. 4 x

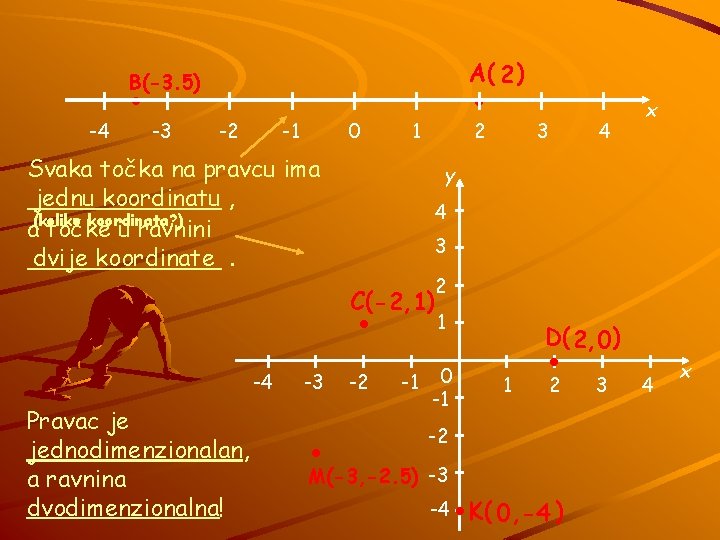
. . A( 2 ) B(-3. 5) -4 -3 -2 0 -1 Svaka točka na pravcu ima jednu koordinatu , _______ koordinata? ) a(koliko točke u ravnini dvije koordinate. _______ 1 2 Pravac je jednodimenzionalan, a ravnina dvodimenzionalna! -3 . 4 y 4 3 . C(-2, 1) -4 3 x -2 -1 2 1 0 -1 -2 M(-3, -2. 5) -3 -4 . D( 2, 0 ) . 1 2 K( 0, -4 ) 3 4 x

2. Proporcionalnost i obrnuta proporcionalnost

Proporcionalne veličine su veličine za koje vrijedi: koliko puta se poveća (smanji) jedna veličina, toliko puta se poveća (smanji) i druga. Proporcionalne veličine imaju konstantan _____ omjer, x: y = konst. Prisjetimo se omjera! Primjer: Da bi majstor dobio određenu nijansu zelene boje, žutu i plavu boju treba izmiješati u omjeru 5: 2. Što to znači? To znači da na svakih 5 dl žute boje treba staviti 2 dl plave. Koliko plave boje treba staviti A na 8 dldlplave? 45 žute? 18 20 dl plave žute na 10 dl žute? 4 dl plave

Reci nekoliko omjera koji su jednaki zadanom omjeru: 8 : 10 = 4 : 5 = 16 : 20 = 80 : 100. . . Dakle, što možemo napraviti s oba člana omjera, pa da dobijemo omjer jednak početnom? Oba člana omjera možemo pomnožiti ili podijeliti s istim brojem. Time ćemo dobiti omjer jednak početnom. Kako se naziva jednakost dvaju omjera, npr. 3 : 7 = 6 : 14 ? RAZMJER ili PROPORCIJA

Kako naći nepoznati član razmjera? Npr. Množimo vanjski član s 8 : x = 6 : 3 6 x = 24 x = 4 / : 6 vanjskim, a unutrašnji s unutrašnjim. (Krenimo s onim parom u kojem je x!) Pogledaj ponovo zadani razmjer, 8 : x = 6 : 3. Jesi li u ovom slučaju logički mogao naći x? Da. Naime, na desnoj strani jednakosti je prvi član (6) dva puta veći od drugoga (od 3). Onda i na lijevoj strani prvi član (8) mora biti dva puta veći od drugoga (od x), pa je x=4.

Kako naći nepoznati član razmjera? Npr. 8 : x = 6 : 3 6 x = 24 x = 4 / : 6 Možeš li i ovaj razmjer riješiti logički: 21 : x = 7 : 4 ? Da. Naime, prvi član na lijevoj strani (21) je tri puta veći od prvog člana na desnoj strani (od 7). Onda i drugi član na lijevoj strani (x) mora biti tri puta veći od drugog člana na desnoj strani (od 4), pa je x=12.

Zadatak: Sa 6 litara benzina Fiat Punto može prijeći 100 km (u prosjeku). U rezervoar stane 40 litara. Koliko kilometara Punto može prijeći sa punim rezervoarom? Rješenje: Koje veličine ovdje imamo? Kakve su to veličine? . . . 6 litara benzina 40 litara benzina 100 km x km 6 : 40 = 100 : x 6 x = 4000 x ≈ 666. 7 / : 6 Fiat Punto sa punim rezervoarom u prosjeku može prijeći oko 667 km.

Obrnuto proporcionalne veličine su veličine za koje vrijedi: koliko puta se poveća (smanji) jedna veličina, toliko puta se smanji (poveća) druga. Obrnuto proporcionalne veličine imaju konstantan _______ umnožak , x∙y = konst. Zadatak: Mali Mario jako voli sladoled. Od djeda je dobio džeparac. Ako će kupovati sladolede za 8 kuna, moći će ih kupiti 3. Ako ih za iste novce želi kupiti dvostruko više, kakva bi im trebala biti cijena? Cijena bi im trebala biti dva puta manja, dakle 4 kune. Kakve su veličine - broj sladoleda i cijena? To su obrnuto proprcionalne veličine.

Zadatak: Stočari Joža i Štef kupili su jednako mnogo hrane za krave. Gazda Joža će s njom svojih 20 krava moći hraniti 15 dana. Koliko će dana gazda Štef s tom hranom moći hraniti svojih 30 krava? Rješenje: Koje veličine ovdje imamo? Kakve su to veličine? . . . 20 krava 30 krava 15 dana x dana 20 : 30 = x : 15 30 x = 300 x = 10 / : 30 Gazda Štef će svoje krave tom hranom moći hraniti 10 dana.

3. Postoci

Primjer: Morska voda sadrži 3 -4 % soli. Što to znači? To znači da 100 kg morske vode sadrži 3 -4 kg soli. A u nekoliko puta većoj (manjoj) količini morske vode ima točno toliko puta više (manje) soli. Dakle, postoci nam govore koliko je nečega u skupini od 100 ___. S nekim jednostavnijim postocima lako računamo i napamet. Prisjetimo ih se! 1 50% = pola = __ = 0. 5 2 1 25% = četvrt = __ = 0. 25 4 3 75% = tri četvrt = __ = 0. 75 4

Primjer: Morska voda sadrži 3 -4 % soli. Što to znači? To znači da 100 kg morske vode sadrži 3 -4 kg soli. A u nekoliko puta većoj (manjoj) količini morske vode ima točno toliko puta više (manje) soli. Dakle, postoci nam govore koliko je nečega u skupini od 100 ___. S nekim jednostavnijim postocima lako računamo i napamet. Prisjetimo ih se! 100% = cijela cjelina = 1 dva puta veće od 200% = = 2 promatrane cjeline pet puta veće od 500% = = 5 promatrane cjeline

Zadatak A: Vlado ima plaću 4100 kuna. Ako Anina plaća čini 200% 150% 100% 25 50 % Vladine plaće, 2050 4100 6150 1025 8200 kn. njezina je plaća _____ Zadatak B: Na parkiralištu je 60 automobila. Od toga je 30 60 15 6 crvenih automobila. 100 50 25 10 %. Tada je crvenih automobila ____ Zadatak C: U jednoj kutiji je 30 cijelih čaša, 50% 10% pakovanja. a to je 75% 60 čaša. 40 Tada je u tom pakovanju ____ 300

A kako postupamo sa "složenijim" postocima? Pretvorimo u razlomke: 7 147 ___ 7%= 147 % = 100 6. 8 ____ 68 ___ 6. 8 % = = 1000 Pretvorimo u decimalne brojeve: 7 % = 0. 07 (Točku ulijevo!) 147 pomaknemo % = 1. 47 dva mjesta 6. 8 % = 0. 068 Pretvorimo u postotke: 4. 7 = 470 % 0. 91 = 91 % 0. 3 = 30 % 3 __ (Točku mjesta = 3 pomaknemo : 5 = 0. 6 dva = 60 % udesno!) 5 9 __ = 9 : 4 = 2. 25 = 225 % 4 6 = 600 % 1 __ = 50 % 2

U postotnom računu imamo tri osnovna tipa zadataka: I. ____ 15. 9 % od 82 je 13 Prvo razlomkom 13 Traži se izrazimo postotak. __ 0. 159 % koji = dio 13: 82 od pretvorimo 82=čini 13! to=u 15. 9 Pa postotak! 82 II. 27 % od 40 je _____ 10. 8 27 "od" znači "puta" ___ ∙ 40 = 0. 27∙ 40 = 10. 8 100 III. 61 % od 114. 8 _____ je 70 / znači "puta" = 70 0. 61 ∙ x"od" : 0. 61 x ≈ 114. 8 Pri rješavanju tekstualnih zadataka, prvo iz teksta zadatka složimo izraz poput gornjih, a zatim ga riješimo.

Zadatak: U hotelu Dupin je 420 gostiju. 40% gostiju su Hrvati. a) Koliko je Hrvata u tom hotelu? 40 % od 420 je _____ 168 40 ___ ∙ 420 = 168 100 U hotelu Dupin je 168 Hrvata. b) Od svih gostiju, 250 je žena, a ostalo su muškarci. Koliki je postotak žena? 60 % od 420 je 250 ____ 250 ___ = 250 : 420 ≈ 0. 6 = 60 % 420 A postotak muškaraca? 100 % - 60 % = 40 % Žene čine 60%, a muškarci 40% gostiju hotela Dupin.

Zadatak: U hotelu Dupin je 420 gostiju. 40% gostiju su Hrvati. a) Koliko je Hrvata u tom hotelu? 40 % od 420 je _____ 168 40 ___ ∙ 420 = 168 100 U hotelu Dupin je 168 Hrvata. c) 8% Čeških gostiju sudjelovalo je na plesnom natjecanju. Oni su činili 5 parova (10 natjecatelja). Koliko je bilo Čeških gostiju? 125 je 10 8 % od _____ 0. 08 ∙ x = 10 x = 125 / : 0. 08 Bilo je 125 Čeških gostiju.

4. Statistika i vjerojatnost

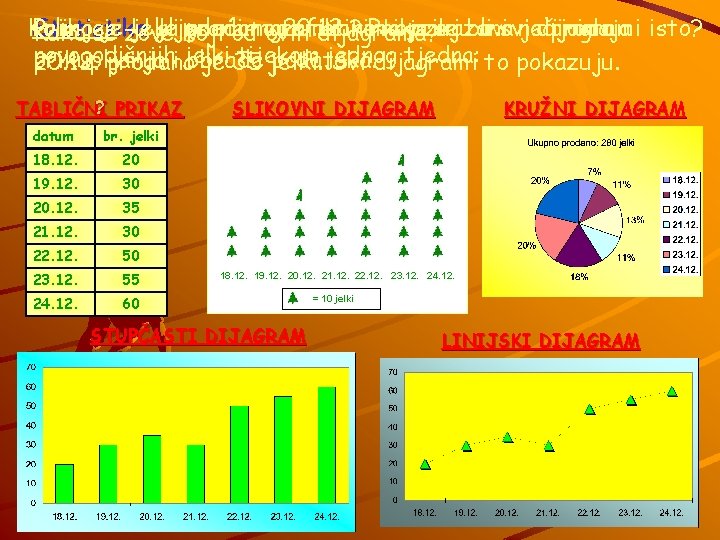
Koliko Statistika Primjer: je zove jelki U je sljedećim grana prodano grafikonima 20. 12. ? Prikazuju koja prikazana se bavi li svi načinima jedijagrami prodaja isto? Kako se koji odmatematike ovih dijagrama? novogodišnjih tijekom jednog tjedna: to pokazuju. prikupljanja i jelki obrade podataka. 20. 12. prodano je 35 jelki. Svi dijagrami ? PRIKAZ TABLIČNI datum br. jelki 18. 12. 20 19. 12. 30 20. 12. 35 21. 12. 30 22. 12. 50 23. 12. 55 24. 12. 60 SLIKOVNI DIJAGRAM KRUŽNI DIJAGRAM 18. 12. 19. 12. 20. 12. 21. 12. 22. 12. 23. 12. 24. 12. STUPČASTI DIJAGRAM = 10 jelki LINIJSKI DIJAGRAM

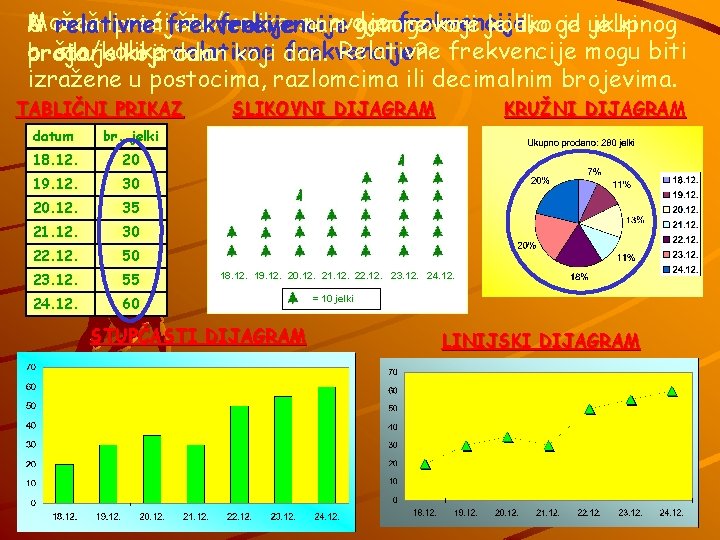
Možeš liprimjeru rećifrekvencije što/kolike su ovdje U ovom A relativne frekvencije nam govore namfrekvencije, govore koji je koliko dio od je ukupnog jelki Relativne frekvencije mogu biti a što/kolike relativne frekvencije? prodano broja jelki koji prodan dan. koji dan. izražene u postocima, razlomcima ili decimalnim brojevima. TABLIČNI PRIKAZ datum br. jelki 18. 12. 20 19. 12. 30 20. 12. 35 21. 12. 30 22. 12. 50 23. 12. 55 24. 12. 60 SLIKOVNI DIJAGRAM KRUŽNI DIJAGRAM 18. 12. 19. 12. 20. 12. 21. 12. 22. 12. 23. 12. 24. 12. STUPČASTI DIJAGRAM = 10 jelki LINIJSKI DIJAGRAM

Zadatak: Izračunaj koliko je prosječno po danu prodano jelki. Kako računamo prosjek? datum br. jelki 18. 12. 20 19. 12. 30 20. 12. 35 21. 12. 30 22. 12. 50 23. 12. 55 24. 12. 60 Prosječnu vrijednost računamo tako da zbrojimo sve vrijednosti, a zatim dobiveni rezultat podijelimo s brojem koliko smo vrijednosti zbrojili. Ovdje ćemo računati: 20 + 35 + 30 + 55 + 60 = 280 : 7 = 40 U prosjeku je po danu prodano 40 jelki.

Vjerojatnost. . . U matematici, vjerojatnost nekog događaja je broj između 0 i 1. Vjerojatnost 1 opisuje siguran događaj. Vjerojatnost 0 opisuje nemoguć događaj. Vjerojatnost 0. 5 opisuje na pola vjerojatan događaj. Ostali brojevi između 0 i 1 opisuju ostale manje ili više vjerojatne događaje. Za vjerojatnost koristimo oznaku P.

Zadatak: U akvariju su ribice. Nestašni mačak Garfild pokušava ih uloviti. Sve su ribice jednako brze. Kolika je vjerojatnost da će Garfild prvo uloviti: 2 1 P(crvena) = ___ = __ 10 5 Općenito: 4 2 ___ __ P(zlatna) = = ? te boje broj ribica 5____________ 10 P(neka boja) = 1 ___ P(ljubičasta) = 10 3 ___ P(prugasta) = 10 ukupan broj ? svih ribica

Zadatak: Mario zna da će mu baka doći u posjetu idući tjedan, ali nema pojma koji bi to dan moglo biti. Kolika je vjerojatnost da će on od prve pogoditi koji će to dan biti? 1 __ P(pogodak) = 7 Kolika je vjerojatnost da on od prve neće pogoditi? 6 P(promašaj) = __ 7 (Na koja dva načina to možemo izračunati? )

Zadatak: U nedjelju će se igrati nogometna utakmica između NK Vesela kopačka i NK Vatreni. Ako je vjerojatnost da pobijedi Vesela kopačka 0. 4, kolika je vjerojatnost da pobijede Vatreni? P(Vatreni) = 0. 6 Zadatak: Na utrci konja vjerojatnost da pobijedi konj Vihor je 70 %. Kolika je vjerojatnost da on ne pobijedi? P(ne Vihor) = 30 %

5. Mnogokuti i krug

Mnogokut je dio ravnine omeđen dužinama koje se ne sijeku. U mnogokute spadaju: - trokuti - četverokuti - peterokuti - šesterokuti, sedmerokuti. . . Za mnogokut ćemo reći da je pravilan ako su mu sve stranice jednakih duljina i svi kutovi jednakih veličina. Koji od likova na gornjim slikama su pravilni? Kako inače nazivamo pravilni trokut? - jednakostraničan trokut A pravilni četverokut? - kvadrat

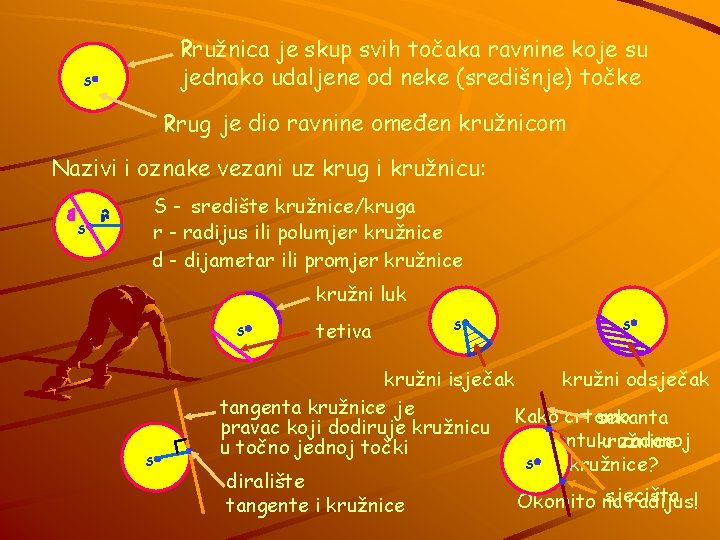
? kružnica je skup svih točaka ravnine koje su jednako udaljene od neke (središnje) točke S ? krug je dio ravnine omeđen kružnicom Nazivi i oznake vezani uz krug i kružnicu: d ? S ? r S - središte kružnice/kruga r - radijus ili polumjer kružnice d - dijametar ili promjer kružnice kružni luk S S tetiva S S kružni isječak kružni odsječak tangenta kružnice je Kako crtamo sekanta pravac koji dodiruje kružnicu tangentukružnice u zadanoj u točno jednoj točki S točki kružnice? diralište sjecišta Okomito na radijus! tangente i kružnice

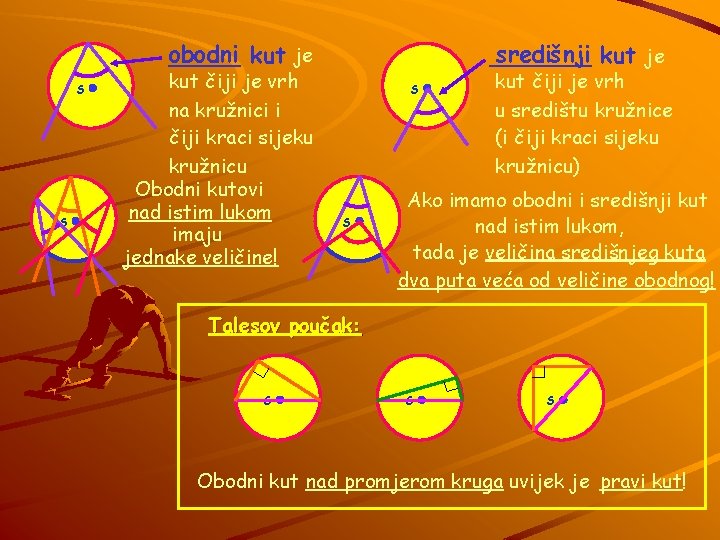
obodni kut je _____ S S kut čiji je vrh na kružnici i čiji kraci sijeku kružnicu Obodni kutovi nad istim lukom imaju jednake veličine! središnji kut je _______ S S kut čiji je vrh u središtu kružnice (i čiji kraci sijeku kružnicu) Ako imamo obodni i središnji kut nad istim lukom, tada je veličina središnjeg kuta dva puta veća od veličine obodnog! Talesov poučak: S S S Obodni kut nad promjerom kruga uvijek je pravi kut!

Opseg (bilo kojeg lika) je duljina njegovog ruba, a površina je veličina njegove unutrašnjosti. Za opseg koristimo m, dm, cm, mm. . . , (koje jedinice? ) a za mjerne površinu m 2, dm 2, cm 2, mm 2. . . Opseg mnogokuta računamo tako da zbrojimo duljine svih njegovih stranica. c c Npr. b b O = a + 2 b + 2 c a Opseg pravilnog sedmerokuta: O = 7 a Opseg pravilnog n-terokuta: O = n∙a S r Opseg kruga: Površina kruga: O = 2 rΠ P = r 2 Π Π ≈ 3. 14 ( r 2 = r∙r )

jednakokračan raznostraničan pravokutan jednakostraničan Ponovimo formule za opsege i površine trokuta i četverokuta. . . trokut Koje vrste trokuta poznajemo (podjela s obzirom na stranice)? c b a ? a a v? c b ? b v? a va c va a O = 3 a P = O = a + 2 b b O= a+b+c P = P = P = a - osnovica b - kraci P = a, b - katete c - hipotenuza Što P je =va? Koji trokut ima "drugačiju" formulu za površinu?

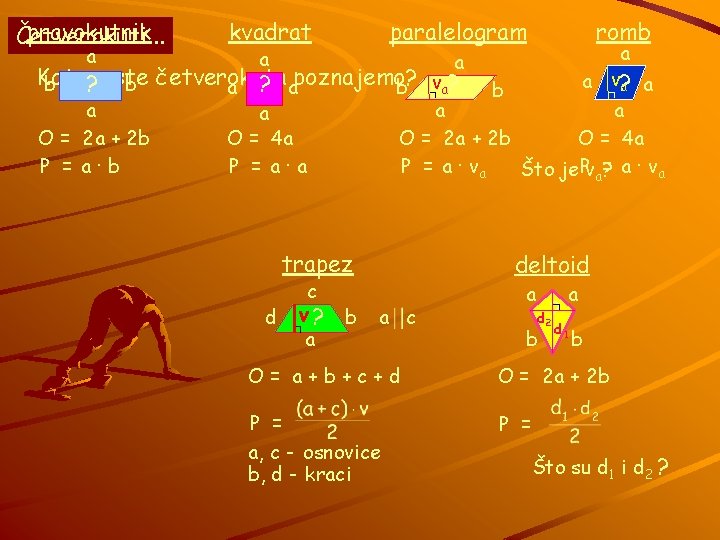
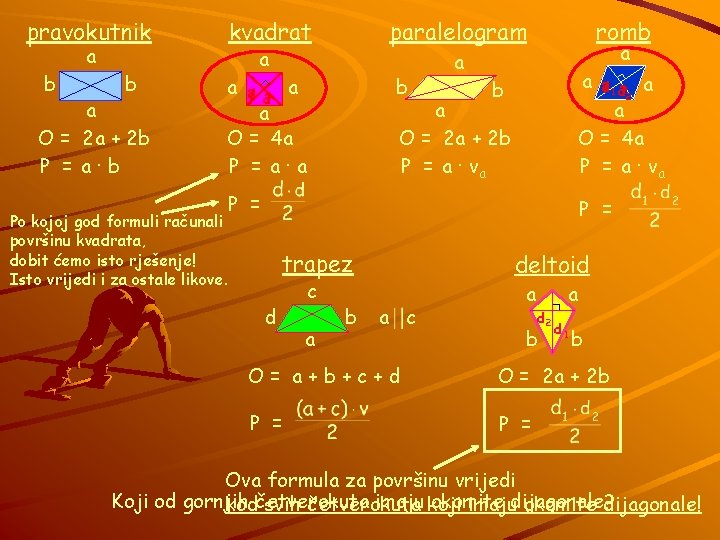
pravokutnik Četverokuti. . . kvadrat paralelogram romb a Koje a v? a a b ? vrste b četverokuta a ? apoznajemo? b va? b a a O = 2 a + 2 b O = 4 a P = a∙b P = a∙a P = a ∙ va Što je Pva? a a a trapez d c v? a b deltoid a c a ? d 2 b a d 1 b O= a+b+c+d O = 2 a + 2 b P = a, c - osnovice b, d - kraci P = Što su d 1 i d 2 ?

pravokutnik kvadrat paralelogram a b b a O = 2 a + 2 b P = a∙b a d ? d? a a romb a a a b a O = 2 a + 2 b P = a ∙ va O = 4 a P = a∙a d ? 1 d? 2 a a O = 4 a P = a ∙ va P = Po kojoj god formuli računali površinu kvadrata, dobit ćemo isto rješenje! Isto vrijedi i za ostale likove. trapez d c a b deltoid a c a ? d 2 b a d 1 b O= a+b+c+d O = 2 a + 2 b P = Ova formula za površinu vrijedi Koji od gornjih imaju koji okomite kodčetverokuta svih četverokuta imajudijagonale? okomite dijagonale!

Izračunaj opseg i površinu ovog lika: ? l O = duljina ruba P 2 O= 7+6+7+l O ≈ 7 + 6 + 7 + 9. 42 ? P 1 7 7 O ≈ 29. 42 cm 6 cm P = P 1 + P 2 P ≈ 42 + 14. 13 P ≈ 56. 13 cm 2 l duljina polukružnice = l rΠ = l 3Π = l ≈3 ∙ 3. 14 l ≈9. 42 cm P 1 = a ∙ b P 1 = 6 ∙ 7 P 1 = 42 cm 2 P 2 = površina polukruga P 2 = P 2 ≈ 14. 13 cm 2

U ovoj cjelini uvježbali smo i kako transformirati formule. Npr. Nađi formulu za va ako je P = . Prvo P = prepišemo∙ 2 zadanu formulu. Riješimo 2 P = a ∙ se va razlomka! Sad sjetimo za a ∙ vse : ašto tražimo formulu! Za va. a = 2 P Onda va mora biti na lijevoj strani! Ako Ponovo sezamijenimo sjetimo za strane. . . što tražimo formulu! Za va. vnije, = a Onda va mora biti sam na lijevoj strani. Riješimo se onoga što smeta na lijevoj strani!

Zbroj kutova: - trokuta je 180˚ - četverokuta je 360˚ - n-terokuta je Kn = (n-2)∙ 180˚ Zadatak: Koliki je (jedan) kut pravilnog deseterokuta? Kako to možemo izračunati? Pravilni deseterokut ima 10 jednakih kutova. Prvo izračunamo zbroj svih 10 kutova, a zatim veličinu jednog. zbroj svih kutova: jedan kut: K 10 = (10 -2)∙ 180˚ K 10 = 8 ∙ 180˚ K 10 = 1440˚ α = K 10: 10 α = 1440˚: 10 α = 144˚ Svaki kut pravilnog deseterokuta ima 144˚.

6. Sličnost trokuta

Za dva trokuta reći ćemo da su slična ako su im: 1. odgovarajuće stranice proporcionalne 2. odgovarajući kutovi jednaki. B c β D A α b γ a δ f C E ε e φ d F ∆ ABC ~ ∆ DEF ako: 1. a : d = b : e = c : f 2. α = δ , β = ε , γ = φ Ako želimo provjeriti jesu li dva trokuta slična, moramo li provjeravati i proporcionalnost svih stranica i jednakosti svih kutova? Ne. O tome nam govore poučci o sličnosti! Koje poučke o sličnosti trokuta znaš?

S-S-S poučak Ako ? dva trokuta imaju proporcionalne stranice, tada su oni slični (tj. tada su im i odgovarajući kutovi jednaki). S-K-S poučak Ako? dva trokuta imaju dvije proporcionalne stranice i ako se podudaraju u kutu između njih, tada su ti trokuti slični (tj. tada su im sve stranice proporcionalne i podudaraju se u sva tri kuta). K-K (-K) poučak Ako ? se dva trokuta podudaraju u kutovima, tada su ti trokuti slični (tj. tada su im i stranice proporcionalne). Dovoljno je provjeriti podudaranje u samo dva kuta.

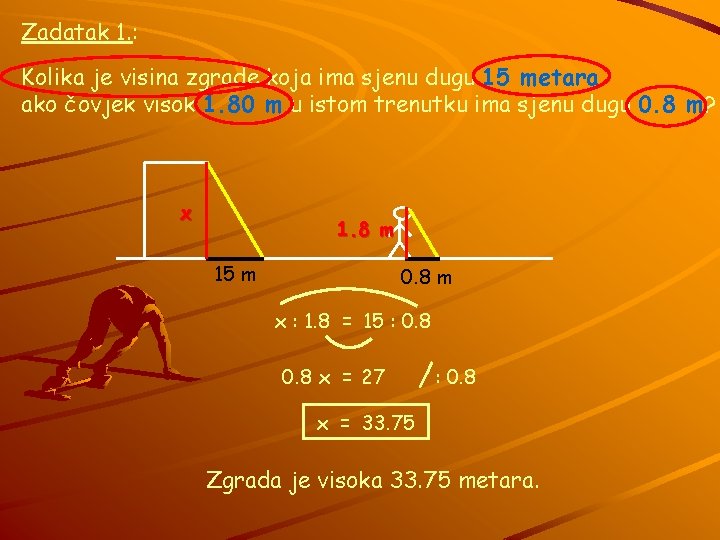
Zadatak 1. : Kolika je visina zgrade koja ima sjenu dugu 15 metara ako čovjek visok 1. 80 m u istom trenutku ima sjenu dugu 0. 8 m? x 1. 8 m 15 m 0. 8 m x : 1. 8 = 15 : 0. 8 x = 27 /: 0. 8 x = 33. 75 Zgrada je visoka 33. 75 metara.

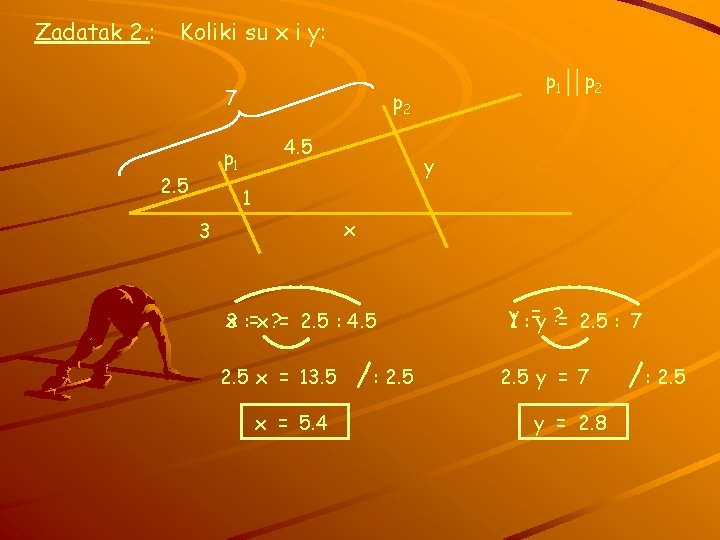
Zadatak 2. : Koliki su x i y: 7 p 2 4. 5 p 1 2. 5 p 1 p 2 y 1 x 3 : =x ? = 2. 5 : 4. 5 2. 5 x = 13. 5 x = 5. 4 /: 2. 5 y 1 : =y ? = 2. 5 : 7 2. 5 y = 7 y = 2. 8 /: 2. 5

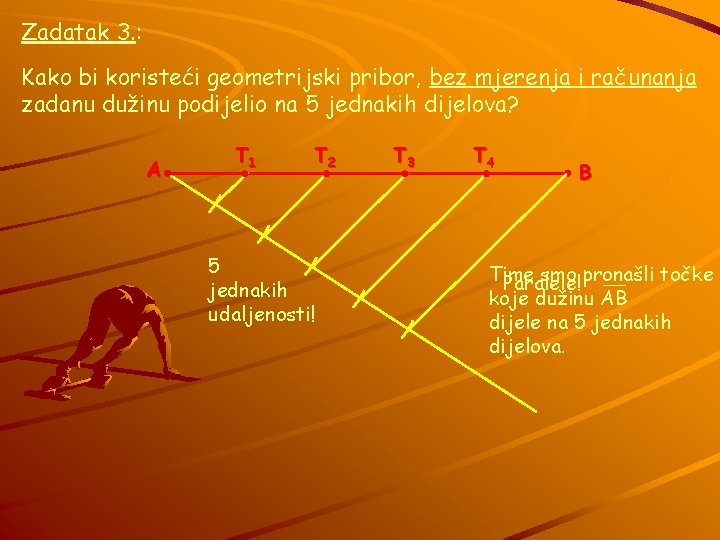
Zadatak 3. : Kako bi koristeći geometrijski pribor, bez mjerenja i računanja zadanu dužinu podijelio na 5 jednakih dijelova? A T 1 T 2 5 jednakih udaljenosti! T 3 T 4 B Time smo pronašli točke Paralele! koje dužinu AB dijele na 5 jednakih dijelova.

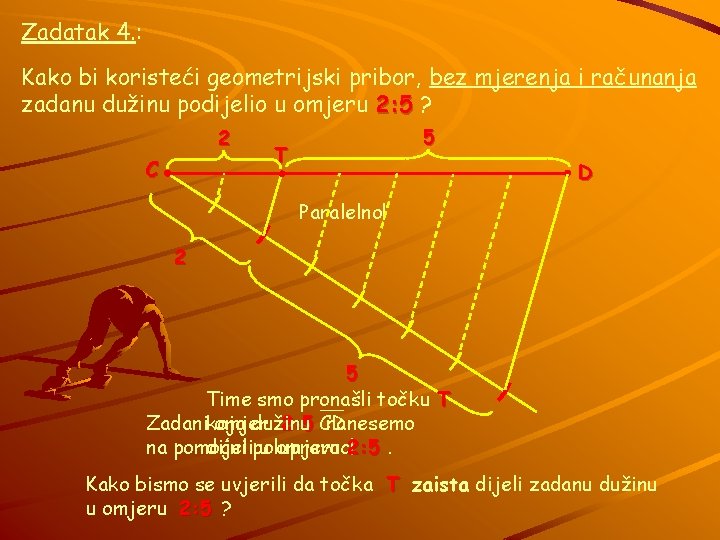
Zadatak 4. : Kako bi koristeći geometrijski pribor, bez mjerenja i računanja zadanu dužinu podijelio u omjeru 2: 5 ? 2 C 5 T D Paralelno! 2 5 Time smo pronašli točku T dužinu Zadanikoja omjer 2: 5 CD nanesemo dijelipolupravac! u omjeru 2: 5. na pomoćni Kako bismo se uvjerili da točka T zaista dijeli zadanu dužinu u omjeru 2: 5 ?

7. Sustav dviju jednadžbi s dvije nepoznanice

Primjer sustava: x + y = 3 3 x - y = 5 x = 2, y = 1 Rj. ( 2, 1 ) Riješiti sustav znači naći brojeve koje u obje jednadžbe možemo uvrstiti umjesto x i y, pa da dobijemo jednakosti. Možeš li napamet (pogađajući) naći rješenje gornjeg sustava?

Sustave možemo rješavati raznim metodama: - pogađanjem (ako je sustav jednostavan) - metodom supstitucije (substituere (lat. ) - zamijeniti) - metodom suprotnih koeficijenata - grafičkom metodom - metodom komparacije. . .

Zadatak 1. : Sljedeće sustave riješi metodom supstitucije (u bilježnicu) : a) 3 x - y = 3 x + 2 y = 8 b) 6 x - 2 y = 2 3 x - 4 y = 22 Rj. ( 2, 3 ) Rj. ( -2, -7 ) Zadatak 2. : Sljedeće sustave riješi metodom suprotnih koeficijenata: a) -3 x - 2 y = 14 3 x - 6 y = 66 Rj. ( 2, -10 ) b) 6 x - 5 y = -16 -4 x - 3 y = -2 Rj. ( -1, 2 )
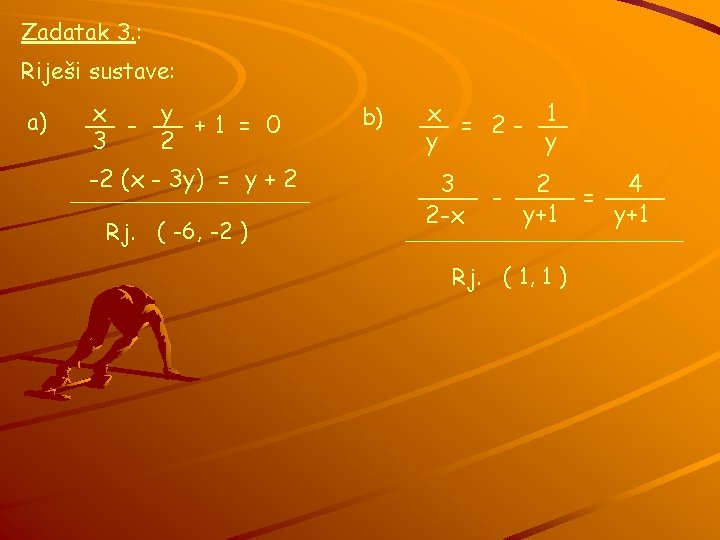
Zadatak 3. : Riješi sustave: a) x y __ - __ + 1 = 0 3 2 -2 (x - 3 y) = y + 2 Rj. ( -6, -2 ) b) x 1 __ = 2 - __ y y 2 4 3 ____ - ____ = ____ y+1 2 -x Rj. ( 1, 1 )

8. Linearna funkcija i jednadžba pravca

Funkcija je pravilo po kojem svakom elementu jednog skupa pridružujemo točno jedan element nekog drugog ili tog istog skupa. Kako čitamo ovo: f(2) = 5 → ef od 2 jednako je 5 Što to znači? To znači da funkcija f broju 2 pridružuje broj 5. 2 ↦ 5 Kako čitamo ovo: g(x) = 2·x → ge od x jednako je 2 puta x Što to znači? Kakva pridruživanja vrši funkcija g? Funkcija g svakom broju x pridružuje 2·x, tj. dvostruki broj.

Zadatak: Zadana je funkcija f(x) = 2 x-7. Izračunajmo što ta funkcija pridružuje brojevima -1 i 3. f (-1) = 2 ∙ (-1) - 7 f (3) = 2 ∙ 3 - 7 f (-1) = -2 - 7 f (3) = 6 - 7 Time smo izračunali f (-1) = -9 f (3) = -1 da ova funkcija broju -1 pridružuje broj -9.

Linearna funkcija je funkcija oblika f(x) = ax + b , pri čemu su a i b racionalni brojevi, a ≠ 0. Za svaku od sljedećih funkcija reci da li je linearna: g(x) = 2 x - 7 → je, a = 2 , b = -7 h(x) = -x + 5 → je, a = -1 , b = 5 f(x) = x → je, a = 1 , b = 0 f(x) = x ∙ x → nije 5 k(x) = 4 x - __ x → nije 8 __ → je, a = -0. 3 , b = f(x) = -0. 3 x + 9 9

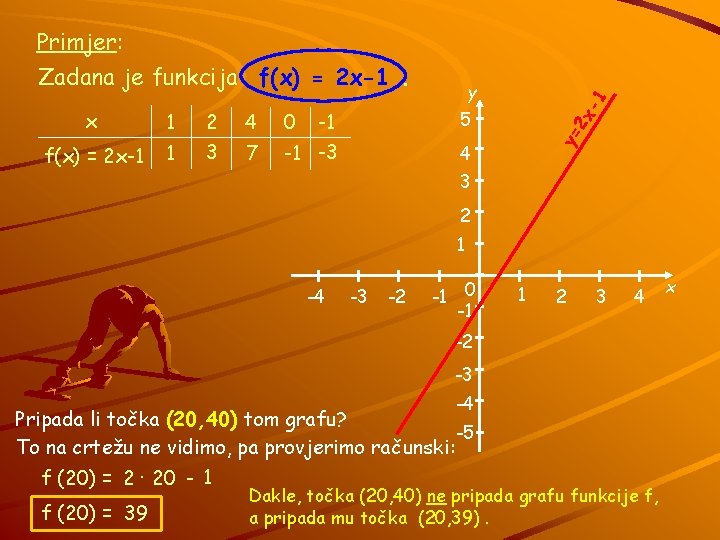
Primjer: Zadana je funkcija f(x) = 2 x-1. Ako xželimo prikazati 1 2 4 što 0 ta-1 funkcija pridružuje nekim brojevima, to možemo učiniti -1 -3 ? pomoću tablice: f(x) = 2 x-1 ? 3 ? 7 ? Kako bismo u koordinatnom sustavu predočili ta ista pridruživanja?

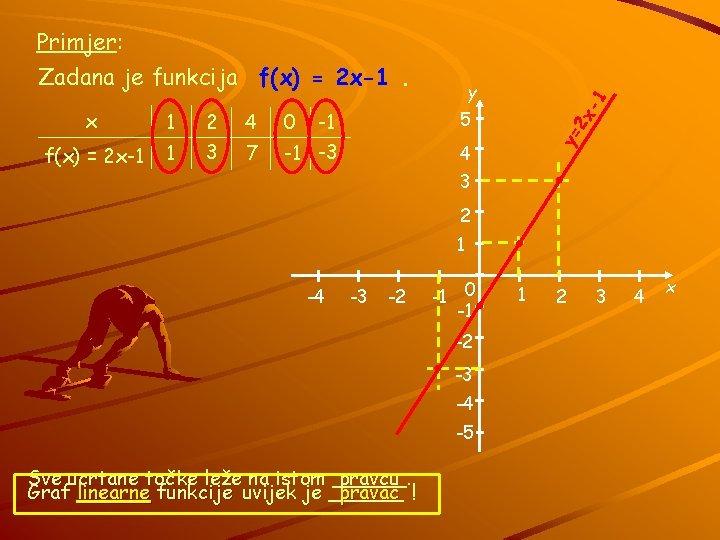
Primjer: Zadana je funkcija f(x) = 2 x-1. 2 4 0 -1 5 f(x) = 2 x-1 1 3 7 -1 -3 4 2 x 1 y= x -1 y 3 2 1 -4 -3 -2 -1 0 -1 -2 -3 -4 -5 Sve ucrtane točke leže na istom ______. pravcu Graf linearne funkcije uvijek je ______ pravac ! 1 2 3 4 x

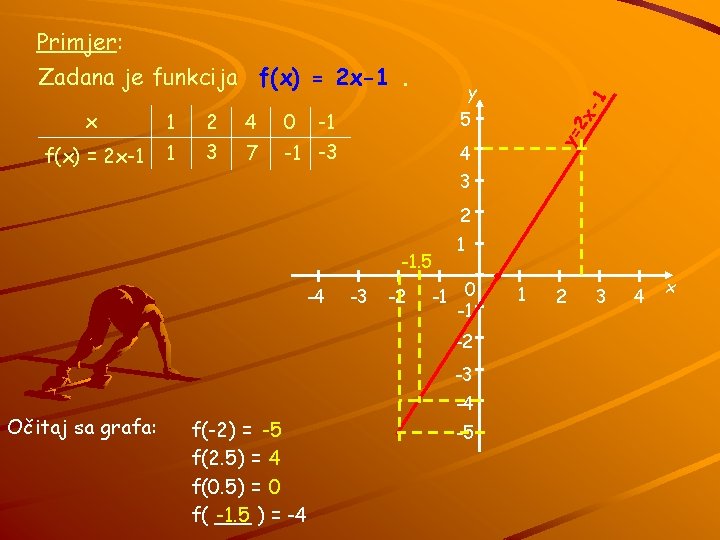
Primjer: Zadana je funkcija f(x) = 2 x-1. 2 4 0 -1 5 f(x) = 2 x-1 1 3 7 -1 -3 4 2 x 1 y= x -1 y 3 2 -1. 5 -4 -3 -2 1 -1 0 -1 -2 -3 Očitaj sa grafa: -4 f(-2) = -5 f(2. 5) = 4 f(0. 5) = 0 f( ___ -1. 5 ) = -4 -5 1 2 3 4 x

Primjer: Zadana je funkcija f(x) = 2 x-1. 2 4 0 -1 5 f(x) = 2 x-1 1 3 7 -1 -3 4 2 x 1 y= x -1 y 3 2 1 -4 -3 -2 -1 0 -1 1 2 3 4 -2 -3 -4 Pripada li točka (20, 40) tom grafu? -5 To na crtežu ne vidimo, pa provjerimo računski: f (20) = 2 ∙ 20 - 1 f (20) = 39 Dakle, točka (20, 40) ne pripada grafu funkcije f, a pripada mu točka (20, 39). x

Nultočka funkcije je broj kojem funkcija pridružuje vrijednost nula. 2 x 5 y= Pogledamo u kojoj točki graf sijeće os x. Dakle, f(0. 5) = 0, Toj točki funkcija f pridružuje nulu! pa je 0. 5 nultočka funkcije f. -1 Kolika je nultočka funkcije f iz prošlog primjera? Možemo li je očitati sa grafa? y 4 3 2 1 -4 -3 -2 -1 0 -1 -2 -3 -4 -5 0. 5 1 2 3 4 x

Nultočka funkcije je broj kojem funkcija pridružuje vrijednost nula. A kako bismo računski našli nultočku iste funkcije, f(x) = 2 x-1 ? Pošto je nultočka vrijednost kojoj funkcija pridružuje nulu, krenimo od: f(x) = 0 2 x - 1 = 0 2 x = 1 /: 2 Nađimo x koji to zadovoljava! x = 0. 5 Došli smo do istog rješenja kao i kad smo očitavali sa grafa, nultočka je broj 0. 5.

Koeficijenti linearne funkcije: f(x) = a x + b koeficijent ? smjera ili nagib - govori nam da li funkcija raste ili pada ? odsječak na osi y - govori nam u kojoj točki graf funkcije sijeće os y Ako je a > 0, tada funkcija _____. raste Ako je a < 0, tada funkcija _____. pada Ako je a = 0, tada funkcija niti ne raste niti ne pada, njezin je graf vodoravan.

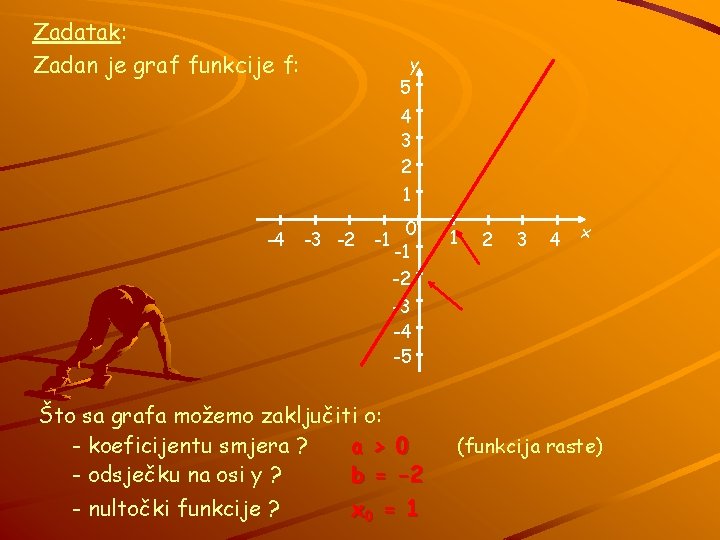
Zadatak: Zadan je graf funkcije f: y 5 4 3 2 1 -4 -3 -2 -1 0 -1 -2 1 2 3 4 x -3 -4 -5 Što sa grafa možemo zaključiti o: - koeficijentu smjera ? a > 0 - odsječku na osi y ? b = -2 - nultočki funkcije ? x 0 = 1 (funkcija raste)

Umjesto f(x) možemo pisati y , npr. y = -2 x + 1. Ako u koordinatnom sustavu nađemo sve točke (x, y) koje to pravcu zadovoljavaju, one će ležati na istom ______. jednadžba pravca Stoga kažemo da je y = -2 x + 1 _______. Kako nacrtati taj pravac? y 5 4 3 2 x 1 2 y = -2 x+1 -1 ? -3 ? 1 -4 -3 -2 -1 0 -1 -2 2 3 4 y= +1 2 x -3 -4 -5 1 x

Ako dva pravca imaju jednake koeficijente smjera, smjera tada su paralelni ti pravci _______. Npr. koji su od ovih pravaca paralelni: y = 3 x - 4 y = 2 x - 4 y = 3 x + 1 y = -2 x - 4

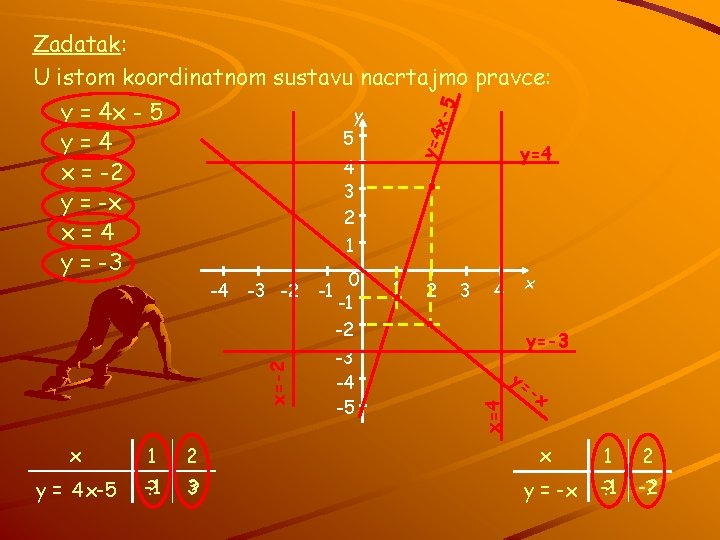
y = 4 x - 5 y=4 x = -2 y = -x x=4 y = -3 x-5 Zadatak: U istom koordinatnom sustavu nacrtajmo pravce: y=4 y 5 4 3 2 y=4 1 -1 0 -1 -2 -3 -4 -5 1 2 3 4 x y=-3 y= x=4 -3 -2 x=-2 -4 -x x 1 2 y = 4 x-5 -1 ? 3 ? y = -x -1 ? -2 ?

Zadatak: x y Nađi jednadžbu pravca koji prolazi točkom (2, -4) i ima koeficijent smjera -1. y = ax + b a, b = ? a = -1 b = -2 y = -x - 2 y = -1 x + b y = -x + b b=? -4 = -2 + b Izračunajmo b! -2 + b = -4 + 2 b = -2

Time smo došli do kraja ponavljanja gradiva 7. razreda. Gradiva je puno, no ako si u 7. razredu redovito radio, vjerujem da si se brzo podsjetio svega što si zaboravio. Puno sreće i uspjeha u 8. razredu!!!

Prezentaciju napravila: Antonija Horvatek rujan 2007.

Ovaj materijal možete koristiti u nastavi, tj. u radu s učenicima. U istu svrhu dozvoljeno je mijenjati ga i prilagoditi svojim potrebama. Za svako korištenje materijala koje nije rad s učenicima, npr. za objavljivanje materijala ili dijelova materijala u časopisima, udžbenicima, na CD-ima. . . , za korištenje na predavanjima, radionicama. . . , potrebno je tražiti i dobiti dozvolu autorice, te vezano uz objavu materijala navesti ime autorice (ako dozvolu dobijete). Ukoliko na bilo koji način koristite moje materijale, bit će mi drago ako dobijem povratnu informaciju, Vaše primjedbe, komentare. . . Antonija Horvatek Matematika na dlanu http: //www. antonija-horvatek. from. hr/
 Kemijske jednadžbe
Kemijske jednadžbe Kviz vjeronauk 5 razred
Kviz vjeronauk 5 razred Rečenični dijelovi 7 razred
Rečenični dijelovi 7 razred Ponavljanje gradiva 4 razreda priroda i društvo
Ponavljanje gradiva 4 razreda priroda i društvo Antonija horvatek 7 razred
Antonija horvatek 7 razred Ponavljanje gradiva 2 razreda vjeronauk
Ponavljanje gradiva 2 razreda vjeronauk Analiza recenice primeri
Analiza recenice primeri Izzi pridruži se razredu
Izzi pridruži se razredu Izzi pridruži se razredu
Izzi pridruži se razredu Petoletka znacenje
Petoletka znacenje Kalendar 2. razred
Kalendar 2. razred Sociometrija u razredu
Sociometrija u razredu Rastanak s razredom
Rastanak s razredom Uredba o varstvu dokumentarnega in arhivskega gradiva
Uredba o varstvu dokumentarnega in arhivskega gradiva Predsjednik razreda
Predsjednik razreda Vrste prezenta
Vrste prezenta Dnevni red roditeljskog sastanka
Dnevni red roditeljskog sastanka Padeži hrvatski
Padeži hrvatski Papirna gradiva
Papirna gradiva Zbirni popis gradiva primjer
Zbirni popis gradiva primjer Razredna pravila
Razredna pravila Vrste nezavisno složenih rečenica
Vrste nezavisno složenih rečenica Ispred nase kucice tekst
Ispred nase kucice tekst Velika nam djela učini gospodin opet smo radosni
Velika nam djela učini gospodin opet smo radosni Velika nam djela učini gospodin opet smo radosni note
Velika nam djela učini gospodin opet smo radosni note Velika nam djela učini gospodin opet smo radosni note
Velika nam djela učini gospodin opet smo radosni note Optimize service management
Optimize service management Tisuću zrnaca skupa
Tisuću zrnaca skupa 1 doc smo
1 doc smo Prinosimo kruh tekst
Prinosimo kruh tekst Yer reaksiyon ortezi
Yer reaksiyon ortezi Iako mnogi jedno smo tijelo
Iako mnogi jedno smo tijelo Valentina zemlić
Valentina zemlić O-ran osc
O-ran osc Smo proposal pdf
Smo proposal pdf Smo cro
Smo cro Ufr slhs
Ufr slhs Velika nam djela učini gospodin opet smo radosni
Velika nam djela učini gospodin opet smo radosni Ufr slhs
Ufr slhs Njegov smo narod i ovce paše njegove
Njegov smo narod i ovce paše njegove Obilježja dramskog teksta
Obilježja dramskog teksta Tri praščića lektira
Tri praščića lektira Bijeli jelen pitanja za ponavljanje
Bijeli jelen pitanja za ponavljanje Zimi uz jadransko more dozrijevaju
Zimi uz jadransko more dozrijevaju Hiperbola stilsko izražajno sredstvo
Hiperbola stilsko izražajno sredstvo Znakovi za nabrajanje u recenici
Znakovi za nabrajanje u recenici Upravni i neupravni govor ponavljanje
Upravni i neupravni govor ponavljanje Potencije zadaci za ponavljanje
Potencije zadaci za ponavljanje Racionalni brojevi 7 razred
Racionalni brojevi 7 razred Drugi svjetski rat ponavljanje
Drugi svjetski rat ponavljanje Zapadna europa ponavljanje
Zapadna europa ponavljanje Gorski krajevi rh ponavljanje
Gorski krajevi rh ponavljanje Ioni i ionski spojevi
Ioni i ionski spojevi Ponavljanje upravnog postupka
Ponavljanje upravnog postupka Ponavljanje stihova u pjesmi
Ponavljanje stihova u pjesmi Padeži ponavljanje
Padeži ponavljanje Zagorski vinograd
Zagorski vinograd Razlomci 5 razred
Razlomci 5 razred Epika 5 razred test
Epika 5 razred test Fizika 8 valovi
Fizika 8 valovi Pjesnicki jezik
Pjesnicki jezik Cijeli brojevi ponavljanje
Cijeli brojevi ponavljanje Družba pere kvržice kviz
Družba pere kvržice kviz E lektire bijeli jelen
E lektire bijeli jelen Pjeni se more analiza pjesme
Pjeni se more analiza pjesme Tri sedmine
Tri sedmine Test iz književnosti 6 razred
Test iz književnosti 6 razred Koji mjeseci pripadaju zimi
Koji mjeseci pripadaju zimi Nominativ
Nominativ Eufonija stilska figura
Eufonija stilska figura Ponavljanje besed
Ponavljanje besed Tijela pravilnog oblika
Tijela pravilnog oblika

























































































