Polynomials Properties Functions Find x Definitions 100 100

Polynomials Properties Functions Find x Definitions 100 100 100 200 200 200 300 300 300 400 400 400 500 500 500 600 600 600 700 800 700 800 900 1000 900 1000

Polynomials for 100 The expression 2 x² - x² is equivalent to Answer: x²

Polynomials for 200 What is the sum of 3 x² + x + 8 and x² - 9 ? Answer: 4 x² + x - 1

Polynomials for 300 What is the answer when (x² - 5 x - 2) is subtracted from (-6 x² - 7 x - 3) ? Answer: -7 x² -2 x - 1

Polynomials for 400 What is the difference between a binomial and a trinomial? Answer: A binomial has two terms and the trinomial has three terms.

Polynomials for 500 Which expression is equivalent to -3 x(x - 4) - 2 x(x + 3)? Answer: -5 x² + 6 x

Polynomials for 600 What is (5 x – 4 y) – (5 x + 4 y) equivalent to? Answer: -8 y

Polynomials for 700 What is the answer when (x² - 5 x - 2) is subtracted from (-6 x² - 7 x - 3) ? Answer: -7 x² -2 x - 1

Polynomials for 800 When (c + 8) and (c - 5) are multiplied, what type of polynomial do we get as the product? What is its degree? Answer: The product is a trinomial (c² + 3 c – 40) of degree two.

Polynomials for 900 • What is the difference when 5 g² - 4 g + 11 is subtracted from 9 g² - 4 g? • What do we call an expression like this? Answer: 4 g² - 11 and we call it a binomial (two terms).

Polynomials for 1000 • 3 x² 4 x 2 6 x³ 9 x² 8 x² 12 x 4 x 6 Answer: 6 x³ + 17 x² + 16 x + 6

Properties for 100 ab + cd cd + ab Which property is illustrated above? Answer: Commutative for addition

Properties for 200 • Answer: The Distributive Property

Properties for 300 Name the property illustrated below Answer: The Distributive Property

Properties for 400 If M, P and Q represent integers, M +(P + Q) = (M + P) + Q is an example of which property? Answer: The Associative Property

Properties for 500 Indicate if the following equation is sure to have a solution set of all real numbers. Explain your answer. �� + �� = �� + �� Answer: Yes, the two expressions are algebraically equivalent by application of the Commutative Property.

Properties for 600 The statement 2 + 0 = 2 is an example of the use of which property of real numbers? 1) associative 2) additive identity 3) additive inverse 4) distributive Answer: 2) The Additive Identity Property

Properties for 700 While solving the equation 4(x + 2) = 2, Kim wrote 4 x + 2 = 28. Which property did she use? 1) distributive 2) associative 3) commutative 4) None of the above Answer: 4) None of the above since the statement is false.

Properties for 800 Identify the property illustrated by each statement: a) 4 (m + 2) = 4 m + 8 b) 3(4 x) = (4 x)3 c) ¼(4) = 1 d) -8 (1) = -8 Answer: a) The Distributive Property b) The Commutative Property for Multiplication c) The Inverse for Multiplication d) The Identity for Multiplication

Properties for 900 Indicate the properties illustrated in the following statements: 1) a + (-a) = 0 2) a (0) = 0 Answer: 1) The Additive Inverse Property 2) The Zero Property

Properties for 1000 Identify the two properties used to obtain each of the two indicated steps Answer: The Distributive and Associative Properties.

Functions for 100 What type of function is y = x² + 51 x ? Answer: This an example of a quadratic function because its highest degree is 2.

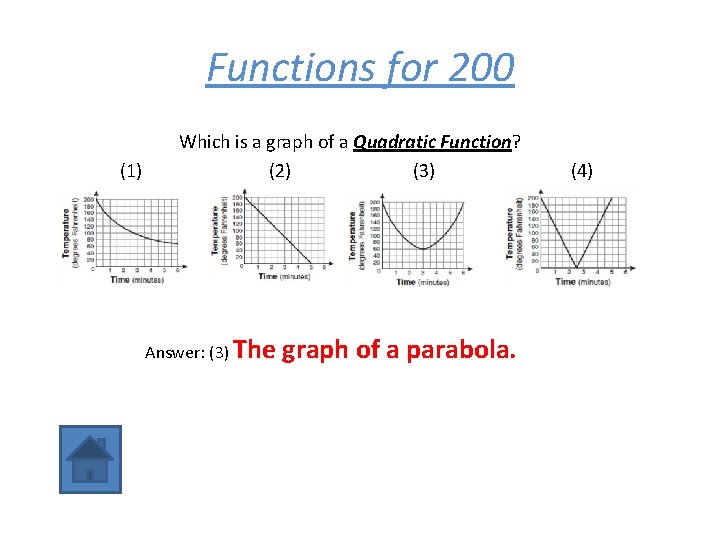
Functions for 200 (1) Which is a graph of a Quadratic Function? (2) (3) Answer: (3) The graph of a parabola. (4)

Functions for 300 Compare the rates of change for A and B. B A Profit Year Which one has a greater change? Answer: The rate of change for B.

Functions for 400 This table gives data from a plant growth experiment. Time (weeks) Height (cm) 3 4. 6 4 5. 8 7 9. 4 What is the rate of growth of the plant? Answer: The rate of growth is 1. 2 cm per week.

Functions for 500 Organize the following function in ascending order: m(x) = x² + 11 x³ - 5 + 20 x. Answer: m(x) = -5 + 20 x + x² + 11 x³

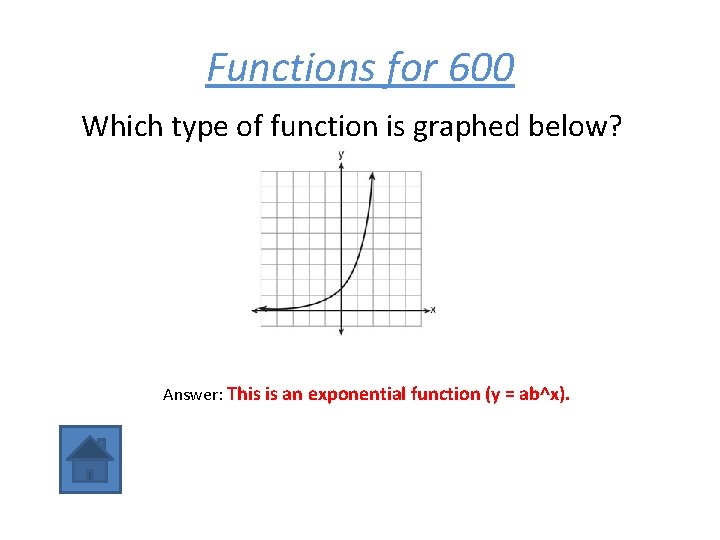
Functions for 600 Which type of function is graphed below? Answer: This is an exponential function (y = ab^x).

Functions for 700 In a linear equation, the independent variable increases at a constant rate while the dependent variable decreases at a constant rate. What type of slope does this line have? Answer: The slope of this line is negative.

Functions for 800 Organize the following function in descending order and determine its degree: m(x) = x² + 11 x³ - 5 + 20 x. Answer: m(x) = 11 x³ + x² + 20 x – 5 and third degree (cubic).

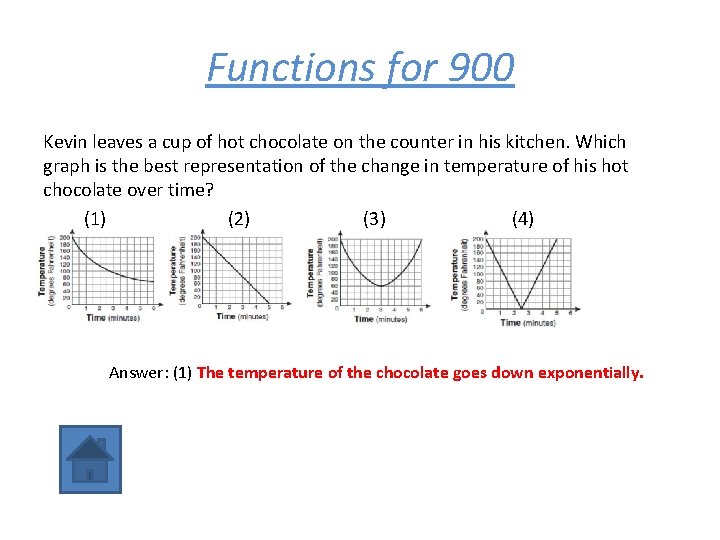
Functions for 900 Kevin leaves a cup of hot chocolate on the counter in his kitchen. Which graph is the best representation of the change in temperature of his hot chocolate over time? (1) (2) (3) (4) Answer: (1) The temperature of the chocolate goes down exponentially.

Functions for 1000 Amy tossed a ball in the air in such a way that the path of the ball was modeled by the equation y = −x² + 6 x. In the equation, y represents the height of the ball in feet and x is the time in seconds. At what time, x, is the ball at its highest point? Answer: At x = 3 sec, the ball is at its highest point.

Find x for 100 2 x + 4 = -6 x = ____ Answer: x = -5

Find x for 200 Is a TRUE or FALSE numerical sentence when x = -5? ( Answer: x³ - 125) = 0 This is a FALSE numerical sentence when x = -5. -125 – 125 ‡ 0

Find x for 300 The average of �� and x is −�� if x = _____. Answer: x = -23

Find x for 400 �� + �� ² = −�� Answer: x = -13

Find x for 500 1___ = _1_ x– 2 4 Answer: x=6

Find x for 600 Consider the equation �� + x = ����. Complete the table below: THE NUMBER SENTENCE TRUTH VALUE Let x = 0 Let x = -7 Let x = 5 Let x = 1 + √ 9 THE NUMBER SENTENCE TRUTH VALUE Let x = 0 �� + 0 = ���� FALSE Let x = -7 �� + (-7) = ���� FALSE Let x = 5 �� + 5 = ���� TRUE Let x = 1 + √ 9 �� + 4 = ���� FALSE

Find x for 700 Consider the algebraic equations �� +�� = �� and (�� +�� )² =����. a) Are these true numerical sentences if �� = �� ? b) Find another value for x besides 3 that would make the second a true numerical sentence. Answer: a) Yes, x = 3 is a solution to both equations. b) x = -5

Find x for 800 a) Determine whether the following number sentence is TRUE or FALSE. 3² X 4² = 12² b) Solve for x: _x²_ = 4² 3² Answer: a) True sentence b) x = 12

Find x for 900 Solve for x: -2 + x = 3. Present the solution set in words, in set notation and also graphically. In words: -2 + x = 3 has the solution x = 5 In set notation: The solution set is { 5 }. In a graphical Representation:

Find x for 1000 Determine the values for x that would make this statement true and provide a graphical representation on a number line. x² = ���� Answer: x = -5 and x = 5

Definitions for 100 Coefficient Answer: A Coefficient is a number used to multiply a variable example, 4 x means 4 times x, so 4 is a coefficient). (In the

Definitions for 200 Operator Answer: An Operator is a symbol (such as +, ×, -, etc) that represents an operation.

Definitions for 300 Variable A symbol for a number we do not know yet. It is usually a letter like x or y. Example: in 4 x - 7 = 5, x is the variable. If it is not a variable it is called a Constant. Answer:

Definitions for 400 Term Answer: A Term is either a single number or a variable, or numbers and variables multiplied together. Examples: 5 4 x -7 5

Definitions for 500 Like Terms Answer: Terms with the same variables (letters) and Exponents (powers).

Definitions for 600 Constant Answer: A Constant is a fixed value. In Algebra, a constant is a number on its own, or sometimes a letter such as a, b or c to stand for a fixed number. Example: in “ 4 x - 7 = 5", 7 and 5 are constants.

Definitions for 700 Algebraic Expression Answer: An algebraic expression is a mathematical phrase that can contain ordinary numbers, variables (like x or y) and operators (like add, subtract, multiply, and divide). Examples: 23 3 p 4 m²³ a+1 a² - b -5 m³ + 2 n³+ 1

Definitions for 800 Algebraic Equation An equation is a math sentence that says that 2 things are equal. An equation always has an equal (=) sign. The thing or things that are on the left side of the equal sign are equal to the things on the right side of the equal sign. Here a few equations: x = 5 m – 9 = 14 p² = 16 x + y = 12 a² + b² = c² Answer:

Definitions for 900 Identify the expressions and the equations (1) 14 x³ + 19 y² - 5 z (3) -2 y² + 19 y = 5 Answer: (2) 14 m + 19 = 2 m + 10 (4) 5 w Expressions = 1 and 4 Equations = 2 and 3

Definitions for 1000 4 x³y²z Name the coefficient, variables and exponents Answer: Coefficient = 4 Variables = x, y, and z Exponents = 3, 2, and 1