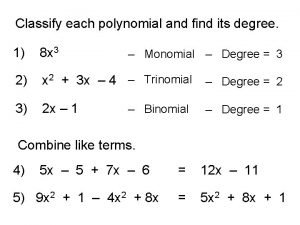Polynomials P 4 Naming Polynomials Terms Degree 1

Polynomials P 4

Naming Polynomials # Terms Degree 1 – Monomial 1 – Linear 2 – Binomial 2 – Quadratic 3 – Trinomial 3 – Cubic 4+ - Polynomial 4 + - 4 th degree, etc. Practice: • If a does not equal 0, the degree of axn is n. • Degree of polynomials is the greatest degree of all its terms • The degree of a nonzero constant is 0. • The constant 0 has no defined degree. 3 x 4 = 4 th degree monomial 5 xy 2= Cubic monomial 3 xy +3 x +4 = Quadratic Trinomial 3 x 4 +5 xy + 6 x + 2= 4 th degree polynomial 3 x 2 +6 x = Quadratic binomial 3 x 3+6 x 2+2 x = Cubic Trinomial

Definition of a Polynomial in x • A polynomial in x is an algebraic expression of the form anxn + an-1 xn-1 + an-2 xn-2 + … + a 1 n + a 0 where an, an-1, an-2, …, a 1 and a 0 are real numbers, an ≠ 0, and n is a non-negative integer. The polynomial is of degree n, an is the leading coefficient, and a 0 is the constant term.

Definition of a Polynomial in x • A polynomial in x is an algebraic expression of the form anxn + an-1 xn-1 + an-2 xn-2 + … + a 1 n + a 0 where an, an-1, an-2, …, a 1 and a 0 are real numbers, an ≠ 0, and n is a non-negative integer. The polynomial is of degree n, an is the leading coefficient, and a 0 is the constant term. Identify the …degree? …leading coefficient? …. and constant term? 3 x 8 + 5 x 4 + 2

Standard Form of a Polynomial Write in order of descending powers of the variable So… 3 x + 5 x 8 - 9 x 3 + 10 should be written 5 x 8 - 9 x 3 +3 x +10

Adding and Subtracting Polynomials (Ex#1) Perform the indicated operations and simplify: (-9 x 3 + 7 x 2 – 5 x + 3) + (13 x 3 + 2 x 2 – 8 x – 6) Solution (-9 x 3 + 7 x 2 – 5 x + 3) + (13 x 3 + 2 x 2 – 8 x – 6) = (-9 x 3 + 13 x 3) + (7 x 2 + 2 x 2) + (-5 x – 8 x) + (3 – 6) = 4 x 3 + 9 x 2 – (-13 x) + (-3) = 4 x 3 + 9 x 2 + 13 x – 3 Group like terms. Combine like terms.

Multiplying Polynomials (Ex #2) The product of two monomials is obtained by using properties of exponents. For example, (-8 x 6)(5 x 3) = -8· 5 x 6+3 = -40 x 9 Multiply coefficients and add exponents. Furthermore, we can use the distributive property to multiply a monomial and a polynomial that is not a monomial. For example, 3 x 4(2 x 3 – 7 x + 3) = 3 x 4 · 2 x 3 – 3 x 4 · 7 x + 3 x 4 · 3 = 6 x 7 – 21 x 5 + 9 x 4. monomial trinomial

Multiplying Polynomials when Neither is a Monomial (Ex #3) • Multiply each term of one polynomial by each term of the other polynomial. Then combine like terms.

Using the FOIL Method to Multiply Binomials last first (ax + b)(cx + d) = ax · cx + ax · d + b · cx + b · d Product of inner outer First terms Outside terms Inside terms Last terms

Ex #3 Multiply: (3 x + 4)(5 x – 3).

Text Example Multiply: (3 x + 4)(5 x – 3). Solution last first F O I L (3 x + 4)(5 x – 3) = 3 x· 5 x + 3 x(-3) + 4(5 x) + 4(-3) = 15 x 2 – 9 x + 20 x – 12 inner = 15 x 2 + 11 x – 12 Combine like terms. outer

The Product of the Sum and Difference of Two Terms (ex #4) DIFFERENCE OF SQUARES • The product of the sum and the difference of the same two terms is the square of the first term minus the square of the second term.

The Square of a Binomial Sum (Ex #5) PERFECT SQUARE TRINOMIAL • The square of a binomial sum is first term squared plus 2 times the product of the terms plus last term squared.

The Square of a Binomial Difference • The square of a binomial difference is first term squared minus 2 times the product of the terms plus last term squared.

Special Products Let A and B represent real numbers, variables, or algebraic expressions. Special Product Example Sum and Difference of Two Terms (A + B)(A – B) = A 2 – B 2 (2 x + 3)(2 x – 3) = (2 x) 2 – 32 = 4 x 2 – 9 Squaring a Binomial (A + B)2 = A 2 + 2 AB + B 2 (A – B)2 = A 2 – 2 AB + B 2 (y + 5) 2 = y 2 + 2·y· 5 + 52 = y 2 + 10 y + 25 (3 x – 4) 2 = (3 x)2 – 2· 3 x· 4 + 42 = 9 x 2 – 24 x + 16 Cubing a Binomial (A + B)3 = A 3 + 3 A 2 B + 3 AB 2 + B 3 (A – B)3 = A 3 – 3 A 2 B – 3 AB 2 + B 3 (x + 4)3 = x 3 + 3·x 2· 4 + 3·x· 42 + 43 = x 3 + 12 x 2 + 48 x + 64 (x – 2)3 = x 3 – 3·x 2· 2 – 3·x· 22 + 23 = x 3 – 6 x 2 – 12 x + 8

Text Example Multiply: a. (x + 4 y)(3 x – 5 y) b. (5 x + 3 y) 2 Solution We will perform the multiplication in part (a) using the FOIL method. We will multiply in part (b) using the formula for the square of a binomial, (A + B) 2. a. (x + 4 y)(3 x – 5 y) Multiply these binomials using the FOIL method. F O I L = (x)(3 x) + (x)(-5 y) + (4 y)(3 x) + (4 y)(-5 y) = 3 x 2 – 5 xy + 12 xy – 20 y 2 = 3 x 2 + 7 xy – 20 y 2 Combine like terms. • (5 x + 3 y) 2 = (5 x) 2 + 2(5 x)(3 y) + (3 y) 2 = 25 x 2 + 30 xy + 9 y 2 (A + B) 2 = A 2 + 2 AB + B 2

Example • Multiply: (3 x + 4)2. Solution: ( 3 x + 4 )2 =(3 x)2 + (2)(3 x) (4) + 42 =9 x 2 + 24 x + 16

Polynomials