Polynomials Investigating Graphs and Transformations 1517 6 5






- Slides: 9

Polynomials Investigating Graphs and Transformations 1/5/17

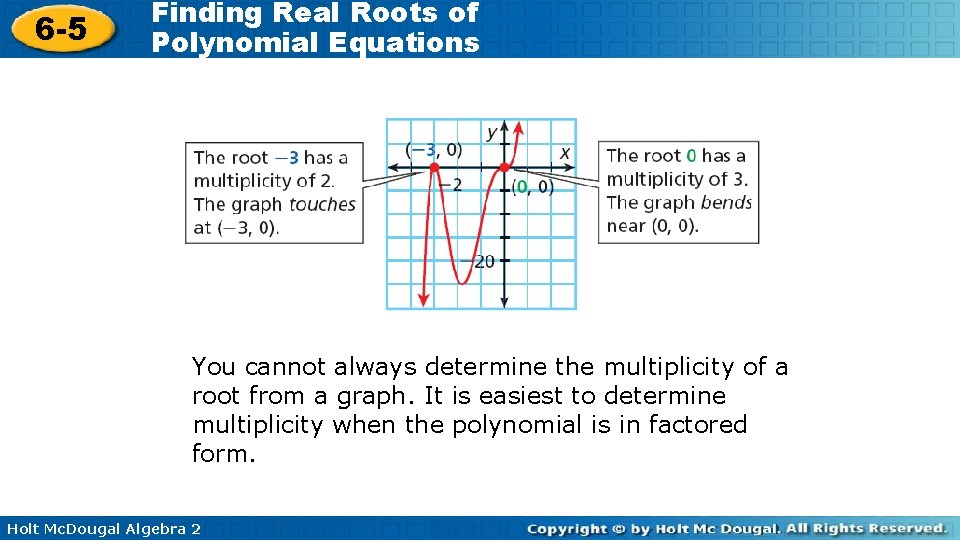
6 -5 Finding Real Roots of Polynomial Equations Sometimes a polynomial equation has a factor that appears more than once. This creates a multiple root. In 3 x 5 + 18 x 4 + 27 x 3 = 0 has two multiple roots, 0 and – 3. For example, the root 0 is a factor three times because 3 x 3 = 0. The multiplicity of root r is the number of times that x – r is a factor of P(x). When a real root has even multiplicity, the graph of y = P(x) touches the x-axis but does not cross it. When a real root has odd multiplicity greater than 1, the graph “bends” as it crosses the x-axis. Holt Mc. Dougal Algebra 2

6 -5 Finding Real Roots of Polynomial Equations You cannot always determine the multiplicity of a root from a graph. It is easiest to determine multiplicity when the polynomial is in factored form. Holt Mc. Dougal Algebra 2

6 -6 Fundamental Theorem of Algebra You have learned several important properties about real roots of polynomial equations. You can use this information to write polynomial function when given in zeros. Holt Mc. Dougal Algebra 2

6 -6 Fundamental Theorem of Algebra Notice that the degree of the function in Example 1 is the same as the number of zeros. This is true for all polynomial functions. However, all of the zeros are not necessarily real zeros. Polynomials functions, like quadratic functions, may have complex zeros that are not real numbers. Holt Mc. Dougal Algebra 2

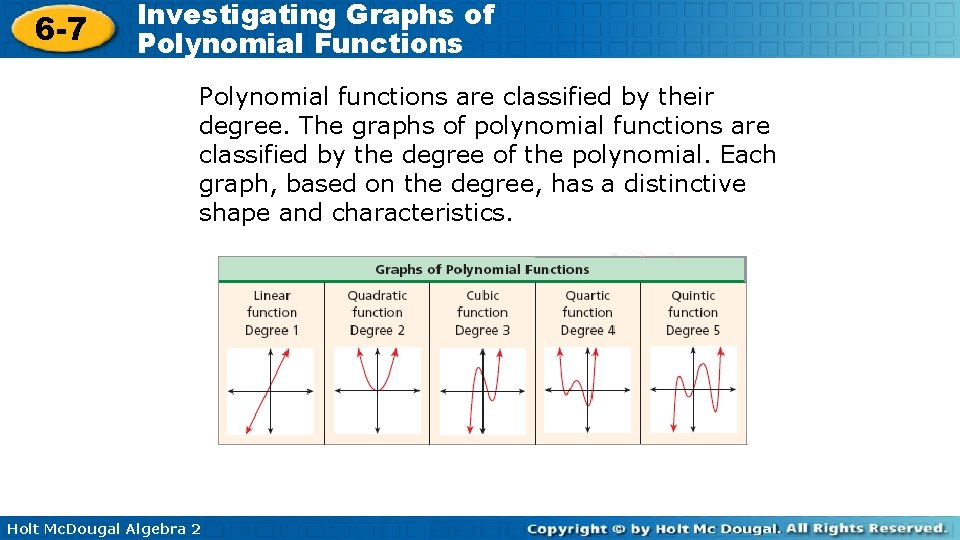
6 -7 Investigating Graphs of Polynomial Functions Polynomial functions are classified by their degree. The graphs of polynomial functions are classified by the degree of the polynomial. Each graph, based on the degree, has a distinctive shape and characteristics. Holt Mc. Dougal Algebra 2

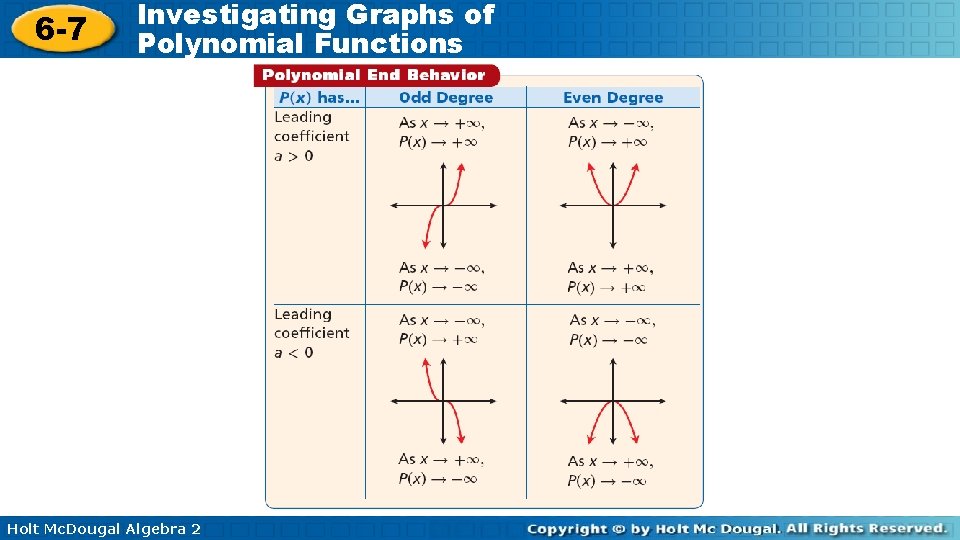
6 -7 Investigating Graphs of Polynomial Functions End behavior is a description of the values of the function as x approaches infinity (x +∞) or negative infinity (x –∞). The degree and leading coefficient of a polynomial function determine its end behavior. It is helpful when you are graphing a polynomial function to know about the end behavior of the function. Holt Mc. Dougal Algebra 2

6 -7 Investigating Graphs of Polynomial Functions Holt Mc. Dougal Algebra 2

6 -8 Transforming Polynomial Functions You can perform the same transformations on polynomial functions that you performed on quadratic and linear functions. Holt Mc. Dougal Algebra 2
 Investigating polynomials
Investigating polynomials Investigating graphs of polynomial functions
Investigating graphs of polynomial functions Investigating graphs of polynomial functions
Investigating graphs of polynomial functions 6-7 investigating graphs of polynomial functions
6-7 investigating graphs of polynomial functions 6-7 investigating graphs of polynomial functions
6-7 investigating graphs of polynomial functions Branches of catholic church
Branches of catholic church Primera de corintios 1517
Primera de corintios 1517 The medieval church (590-1517 ce)
The medieval church (590-1517 ce) Calvinism map
Calvinism map Dell inspiron 1517
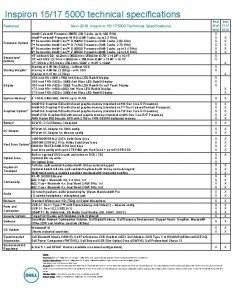
Dell inspiron 1517