Polynomials Functions Polynomial Expressions A polynomial is an

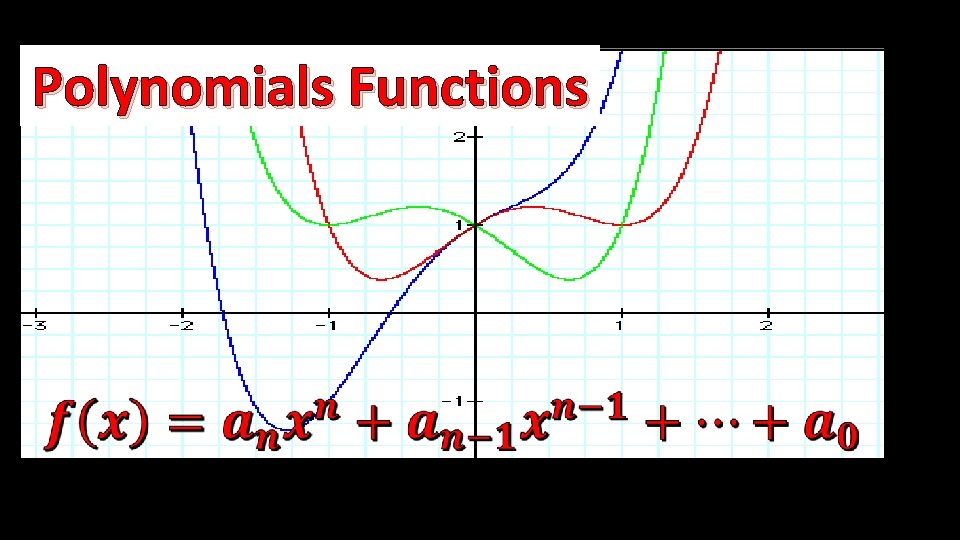
Polynomials Functions

Polynomial Expressions A polynomial is an algebraic expression that is the sum of terms involving variables that has whole number exponents In standard form, it is written in descending order of the degrees.

Standard Form of Polynomial Functions

Examples of Polynomials Monomial (1 term) 2 Binomial ( 2 terms) Trinomial (3 terms) Polynomials with 4 terms

NOT Examples of Polynomials

Factored Form of Polynomials • Polynomials may be written in factored form to explicitly show roots of the polynomials, A. K. A. the xintercepts of the polynomial function. f(x)=a(x-x 1)(x-x 2)(x-x 3) where x 1, x 2, and x 3 are the x-intercepts of the function

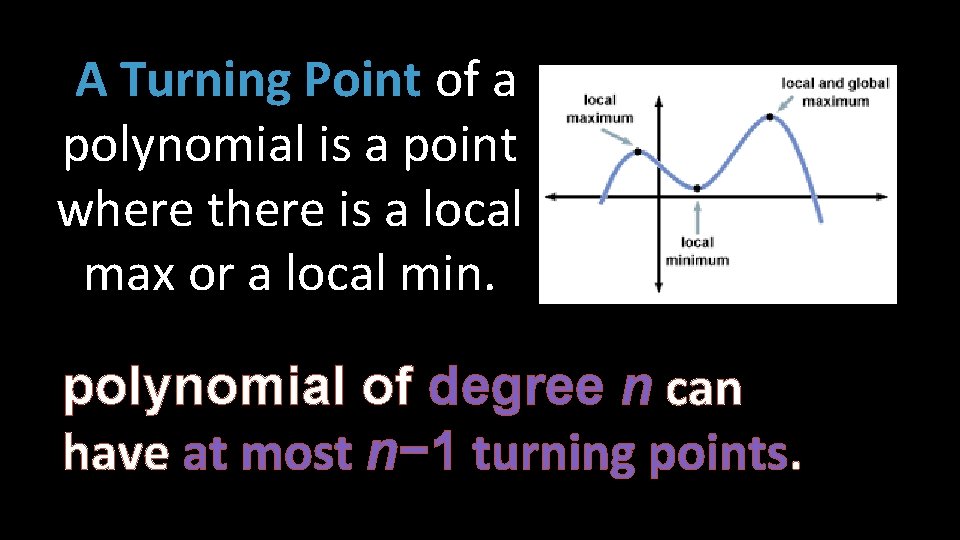
A Turning Point of a polynomial is a point where there is a local max or a local min. polynomial of degree n can have at most n− 1 turning points.

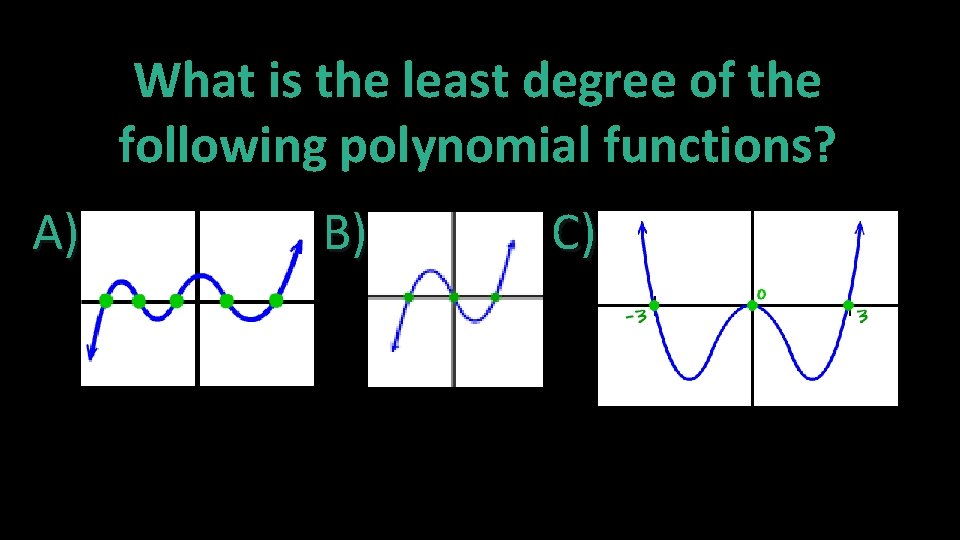
What is the least degree of the following polynomial functions? A) B) C)

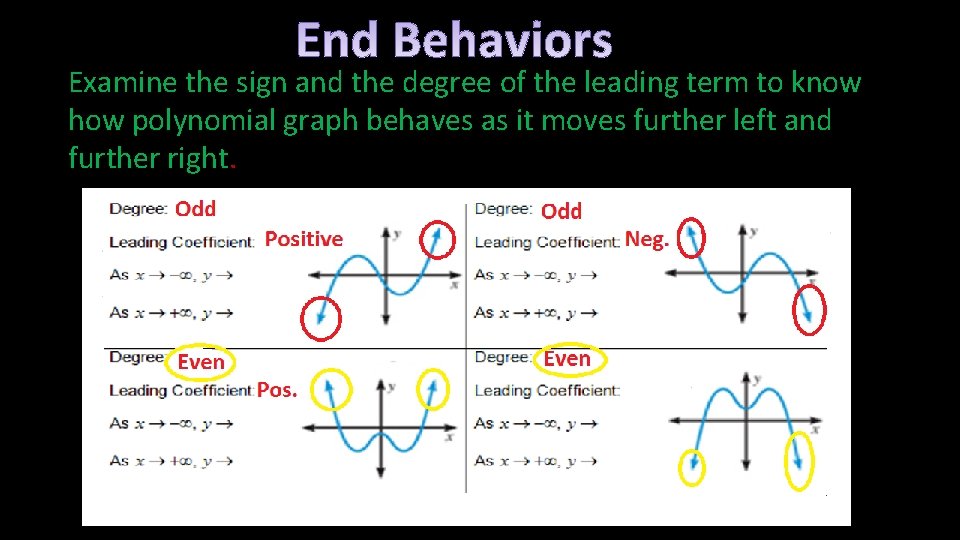
Examine the sign and the degree of the leading term to know how polynomial graph behaves as it moves further left and further right.

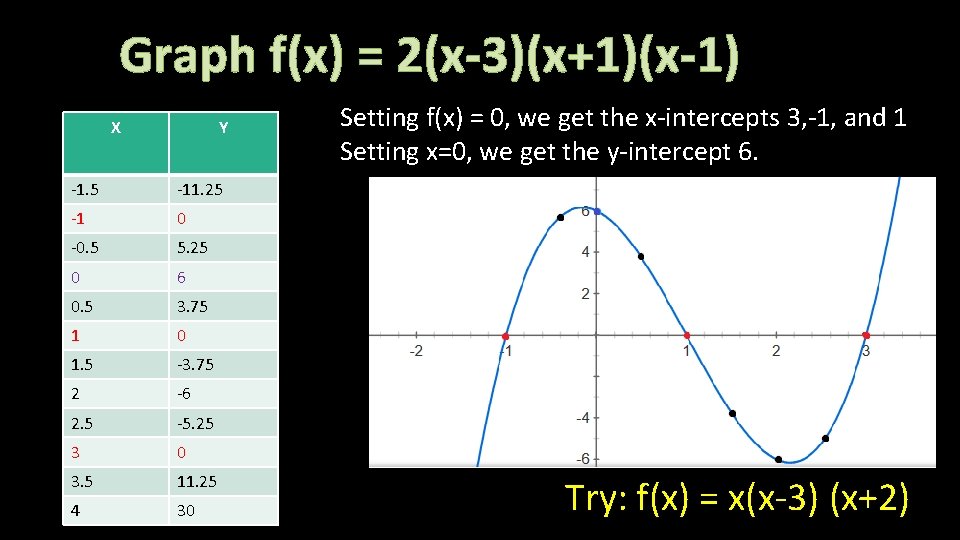
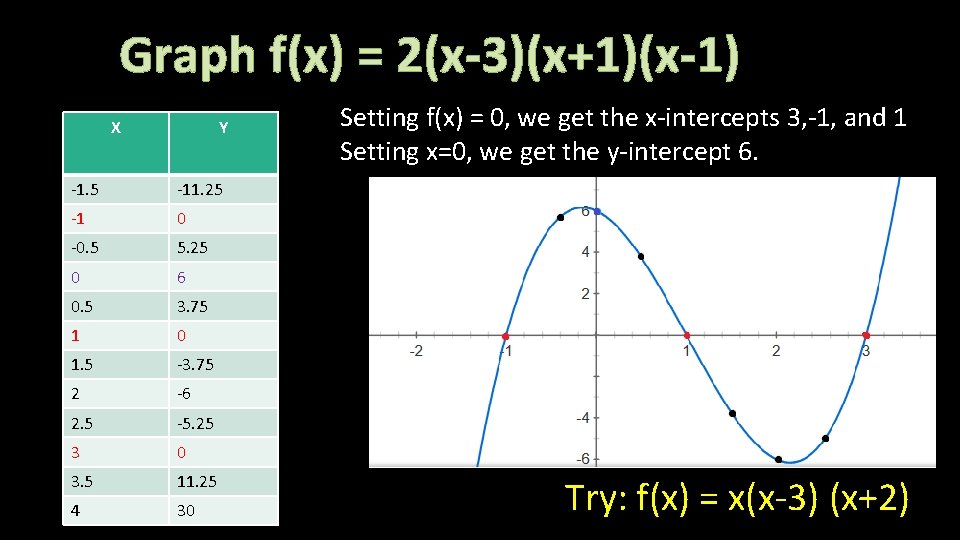
Graphing Factored Form Directions: 1) Find the x-intercepts by putting f(x)= 0 2) Find the y-intercept by putting x=0 3) Choose multiple x-values to find interpolating points 4) Plot all points and connect them with a smooth curve followed with the expected end-behaviors.

Graph f(x) = 2(x-3)(x+1)(x-1) X Y -1. 5 -11. 25 -1 0 -0. 5 5. 25 0 6 0. 5 3. 75 1 0 1. 5 -3. 75 2 -6 2. 5 -5. 25 3 0 3. 5 11. 25 4 30 Setting f(x) = 0, we get the x-intercepts 3, -1, and 1 Setting x=0, we get the y-intercept 6. Try: f(x) = x(x-3) (x+2)

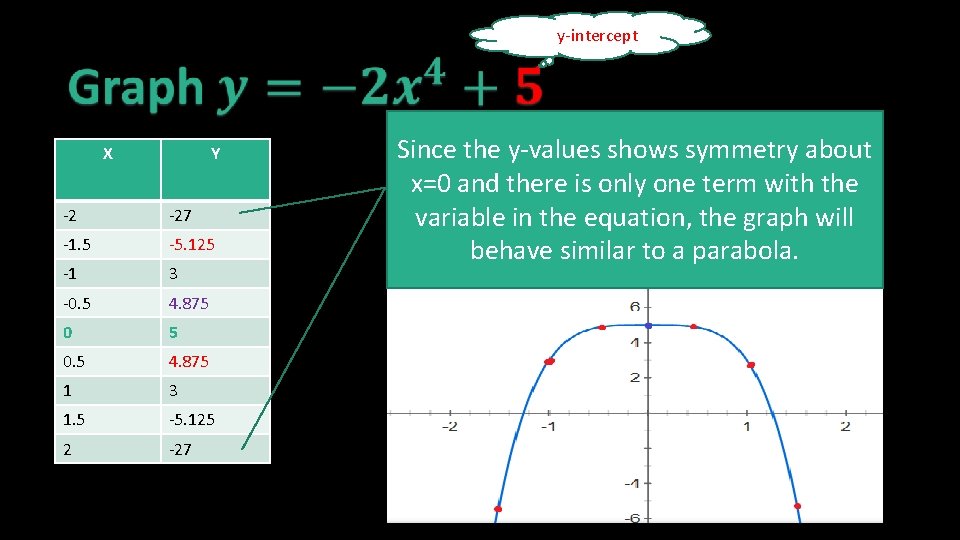
Graphing Standard Form Directions: 1) Find the y-intercept, which is the constant 2) Factor the polynomial (if possible), then find the x-intercepts 3) Choose multiple x-values to find interpolating points 4) Plot all points and connect them with a smooth curve followed with the expected end-behaviors.

The y-intercept X Y -2 -27 -1. 5 -5. 125 -1 3 -0. 5 4. 875 0 5 0. 5 4. 875 1 3 1. 5 -5. 125 2 -27 Since the y-values shows symmetry about x=0 and there is only one term with the variable in the equation, the graph will behave similar to a parabola.

Graph f(x) = 2(x-3)(x+1)(x-1) X Y -1. 5 -11. 25 -1 0 -0. 5 5. 25 0 6 0. 5 3. 75 1 0 1. 5 -3. 75 2 -6 2. 5 -5. 25 3 0 3. 5 11. 25 4 30 Setting f(x) = 0, we get the x-intercepts 3, -1, and 1 Setting x=0, we get the y-intercept 6. Try: f(x) = x(x-3) (x+2)

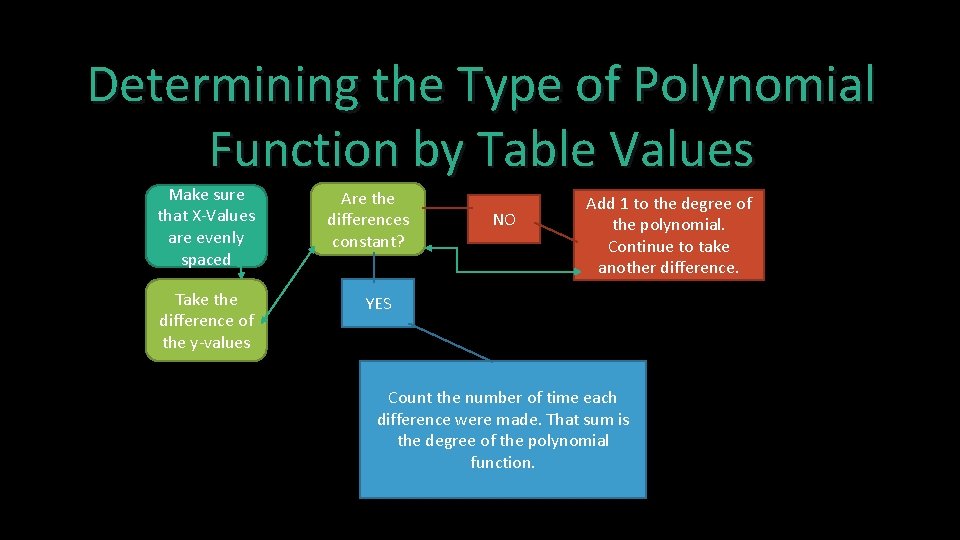
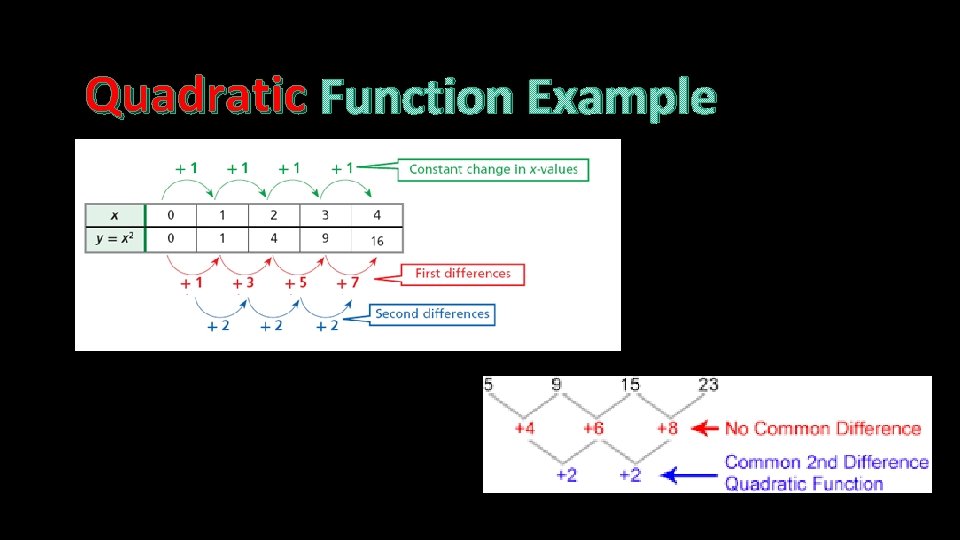
Determining the Type of Polynomial Function by Table Values Make sure that X-Values are evenly spaced Take the difference of the y-values Are the differences constant? NO Add 1 to the degree of the polynomial. Continue to take another difference. YES Count the number of time each difference were made. That sum is the degree of the polynomial function.

Quadratic Function Example

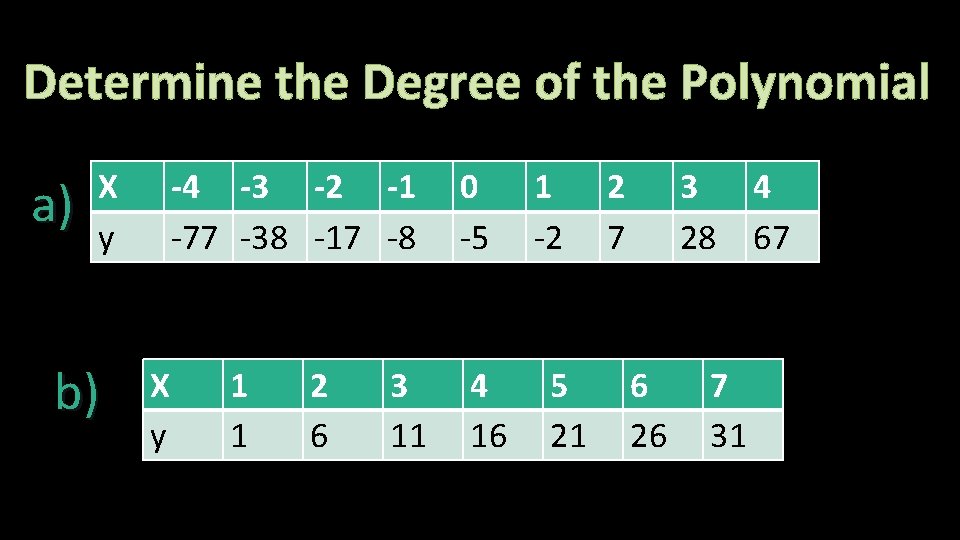
Determine the Degree of the Polynomial X a) y b) -4 -3 -2 -1 -77 -38 -17 -8 X y 1 1 2 6 3 11 0 -5 4 16 1 -2 5 21 2 7 3 28 6 26 7 31 4 67