Polynomial Multiplication with Discrete Fourier Transform Fast Fourier

Polynomial Multiplication with Discrete Fourier Transform Fast Fourier Transform 10/31/2021 FFT 1

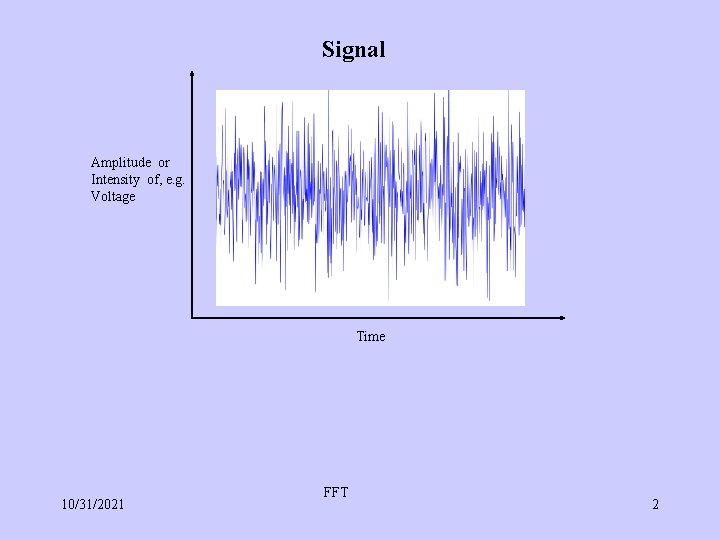
Signal Amplitude or Intensity of, e. g. Voltage Time 10/31/2021 FFT 2

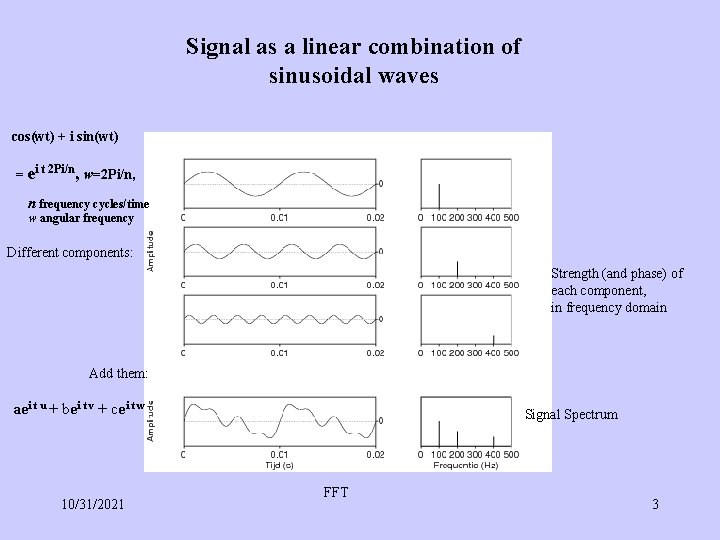
Signal as a linear combination of sinusoidal waves cos(wt) + i sin(wt) = ei t 2 Pi/n, w=2 Pi/n, n frequency cycles/time w angular frequency Different components: Strength (and phase) of each component, in frequency domain Add them: aei t u + bei t v + cei t w 10/31/2021 Signal Spectrum FFT 3

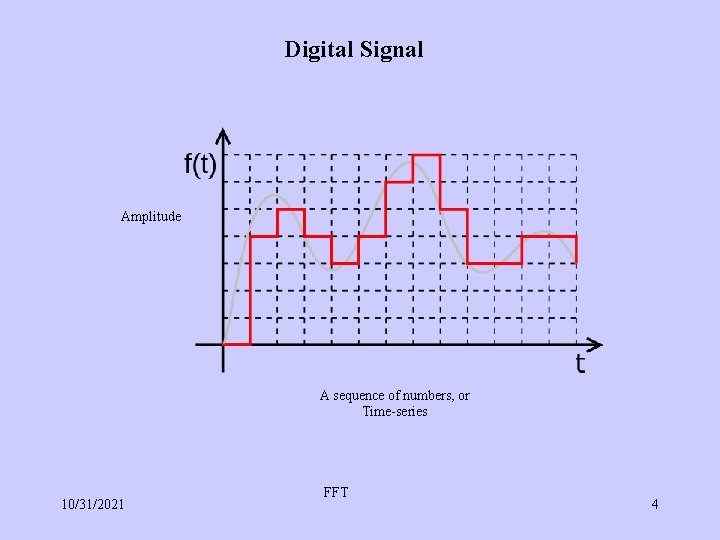
Digital Signal Amplitude A sequence of numbers, or Time-series 10/31/2021 FFT 4

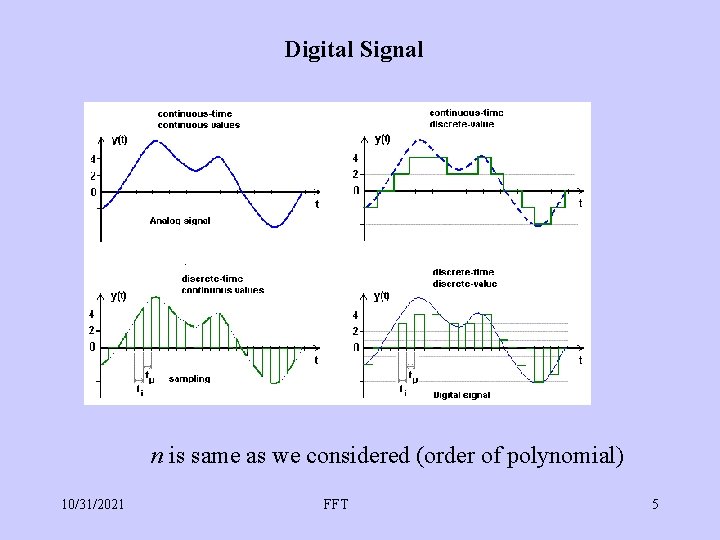
Digital Signal n is same as we considered (order of polynomial) 10/31/2021 FFT 5

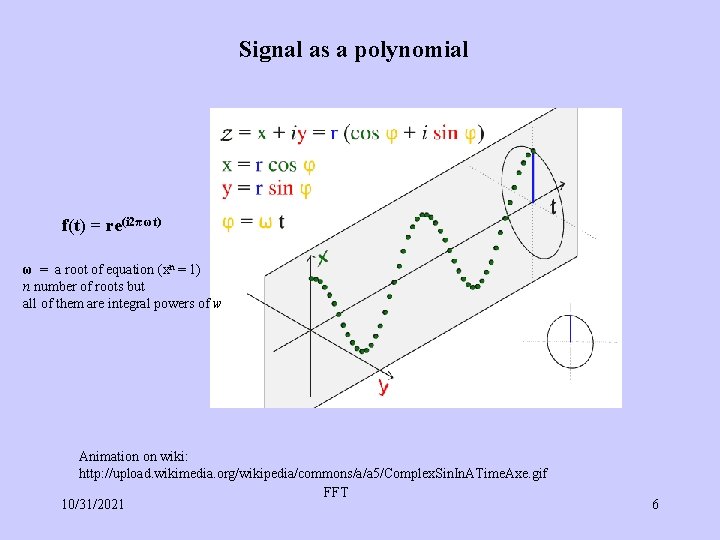
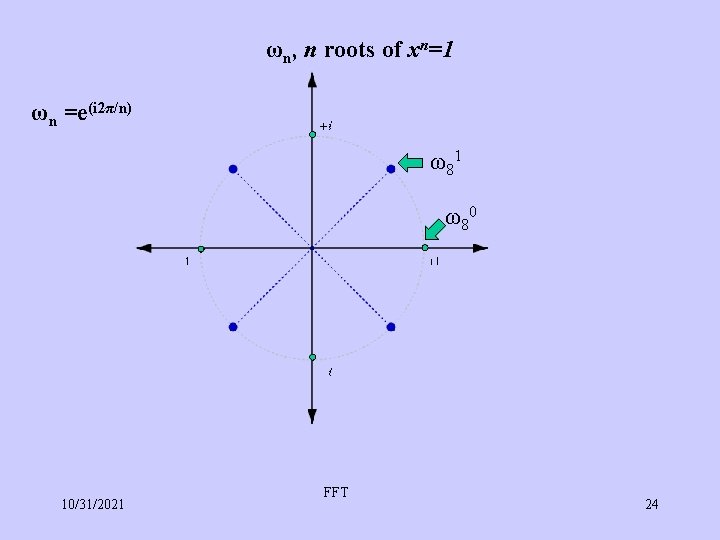
Signal as a polynomial f(t) = re(i 2π ωt) ω = a root of equation (xn = 1) n number of roots but all of them are integral powers of w Animation on wiki: http: //upload. wikimedia. org/wikipedia/commons/a/a 5/Complex. Sin. In. ATime. Axe. gif FFT 10/31/2021 6

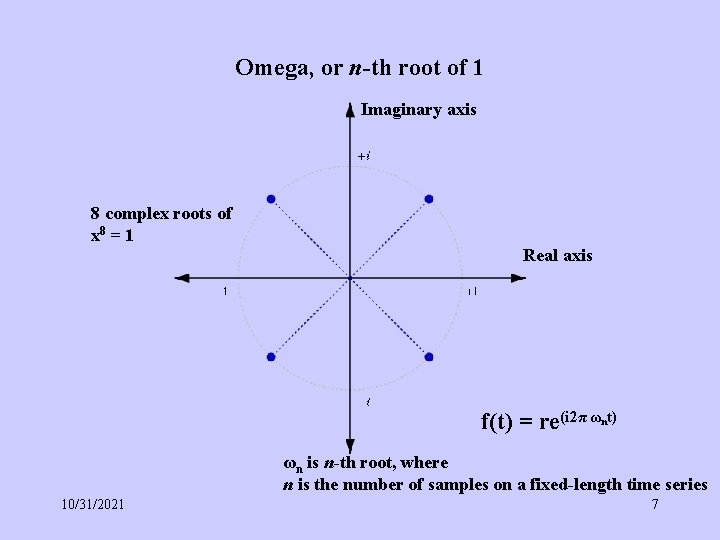
Omega, or n-th root of 1 Imaginary axis 8 complex roots of x 8 = 1 Real axis f(t) = re(i 2π ω t) n ωn is n-th root, where n is the number of samples on a fixed-length time series 10/31/2021 7

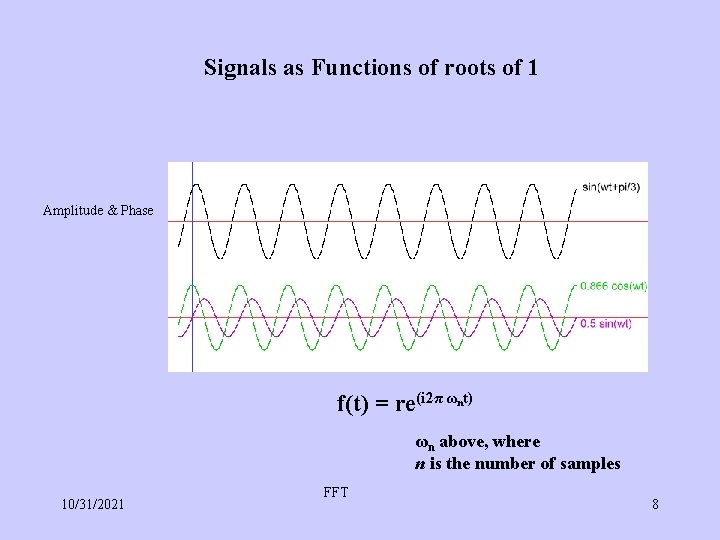
Signals as Functions of roots of 1 Amplitude & Phase f(t) = re(i 2π ω t) n ωn above, where n is the number of samples 10/31/2021 FFT 8

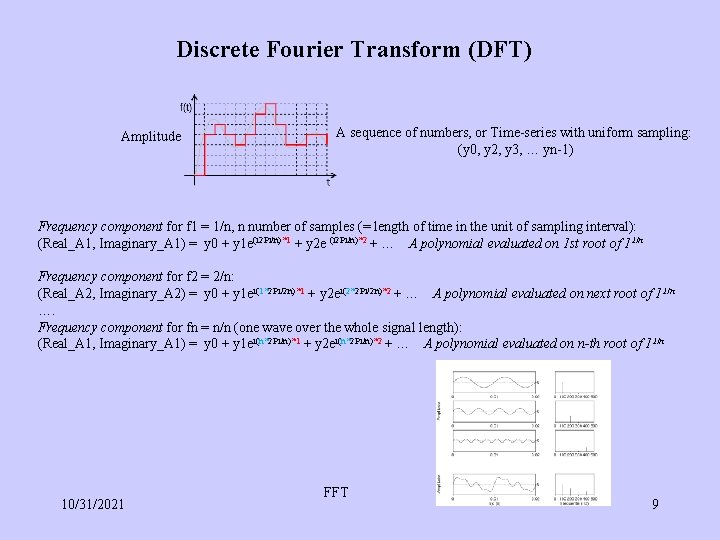
Discrete Fourier Transform (DFT) Amplitude A sequence of numbers, or Time-series with uniform sampling: (y 0, y 2, y 3, … yn-1) Frequency component for f 1 = 1/n, n number of samples (= length of time in the unit of sampling interval): (Real_A 1, Imaginary_A 1) = y 0 + y 1 e(i 2 Pi/n)*1 + y 2 e (i 2 Pi/n)*2 + … A polynomial evaluated on 1 st root of 11/n Frequency component for f 2 = 2/n: (Real_A 2, Imaginary_A 2) = y 0 + y 1 ei(1*2 Pi/2 n)*1 + y 2 ei(2*2 Pi/2 n)*2 + … A polynomial evaluated on next root of 11/n …. Frequency component for fn = n/n (one wave over the whole signal length): (Real_A 1, Imaginary_A 1) = y 0 + y 1 ei(n*2 Pi/n)*1 + y 2 ei(n*2 Pi/n)*2 + … A polynomial evaluated on n-th root of 11/n 10/31/2021 FFT 9

Discrete Fourier Transform (DFT) Frequency component for f 1 = 1/n, n number of samples (= length of time in the unit of sampling interval): (Real_A 1, Imaginary_A 1) = y 0 + y 1 e(i 2 Pi/n) + y 2 e (i 2 Pi/n)*2 + … A polynomial evaluated on 1 st root of 11/n Frequency component for f 2 = 2/n: (Real_A 2, Imaginary_A 2) = y 0 + y 1 ei(2*2 Pi/2 n) + y 2 ei(2*2 Pi/2 n)*2 + … A polynomial evaluated on next root of 11/n …. Frequency component for fn = n/n (one wave over the whole signal length): (Real_A 1, Imaginary_A 1) = y 0 + y 1 ei(n*2 Pi/n) + y 2 ei(n*2 Pi/n)*2 + … A polynomial evaluated on n-th root of 11/n • Polynomial of n-th order: each evaluation takes O(n) time • n evaluations: O(n 2) time • Naïve DFT: O(n 2) • Recursive Divide and Conquer for evaluating on all simultaneously (FFT): O(n log n) 10/31/2021 FFT 10

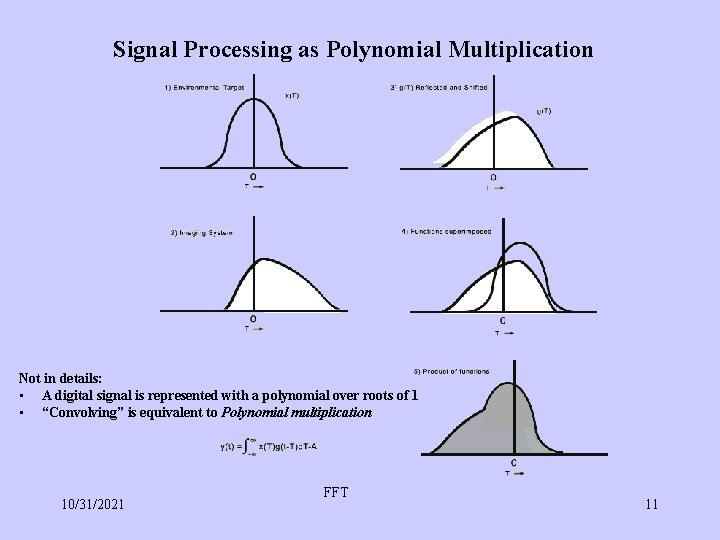
Signal Processing as Polynomial Multiplication Not in details: • A digital signal is represented with a polynomial over roots of 1 • “Convolving” is equivalent to Polynomial multiplication 10/31/2021 FFT 11

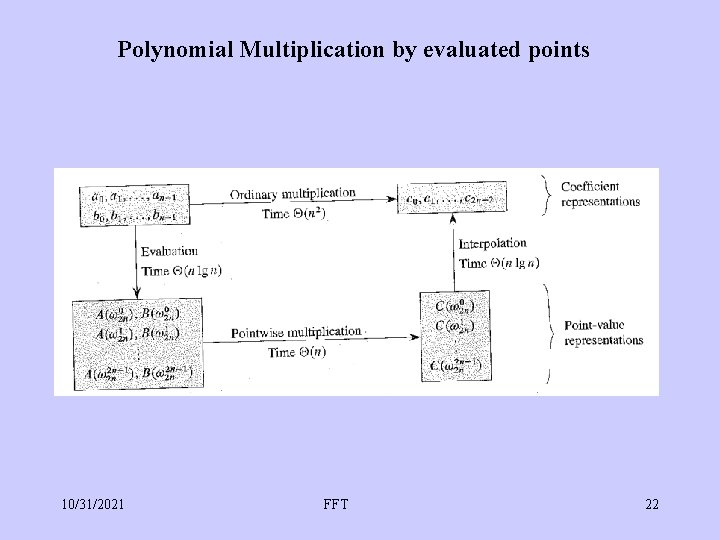
Polynomial Multiplication f(x) = A 0 + A 1 x 1 + A 2 x 2 +. . . + An-1 xn-1 2 Representations: • Coefficients (A 0, A 1, A 2, . . . , An-1) • Evaluated at n points y(x 0), y(x 1), . . . , y(xn-1) • Exchangeable: Given A's, evaluate at n points, • or, Given n points, solve for n coefficients • Traditionally: O(n 2) algorithms for each. • Divide and Conquer DFT: O(n log n) 10/31/2021 FFT 12

Polynomial Multiplication • Given A[0. . n-1] DFT evaluates ==> on wn 0, wn 1, wn 2, . . . , wnn-1, • where wn is n-th root of the equation xn = 1 • Takes O(n) for each evaluation, O(n 2) for n total points • Recursive divide conquer DFT takes O(n log n) time 10/31/2021 FFT 13

Polynomial Multiplication • Given A[0. . n-1] DFT evaluates ==> on wn 0, wn 1, wn 2, . . . , wnn-1, • where wn is n-th root of the equation xn -1 = 1 • Takes O(n) for each evaluation, O(n 2) for all • Recursive divide conquer DFT takes O(n log n) time • Why evaluate on those complex points, over n roots of 1 (DFT)? • To develop O(n log_n) FFT – for simultaneous evaluation on all of them. • Then convert it to iterative and parallelizable FFT 10/31/2021 FFT 14

Primary use of Efficient Polynomial Multiplication: Convolution of Two Signals Used for filtering Another advantage: wn = e^(i*2 pi(theta)/n) = cos(theta) + i*sin(theta), n number of samples This allows us to do Fourier analysis of a signal, e. g. for compression A[] => y() is DFT done by FFT: transforms from time series to its frequency spectrum, and y() => A[] by inverse. FFT (or IFFT): transforms a frequency spectrum to time series 10/31/2021 FFT 15

Polynomial Multiplication Standard Procedure: A(x) = a 0 + a 1 x 1 + a 2 x 2 + … an-1 xn-1 B(x) = b 0 + b 1 x 1 + b 3 x 2 + … bn-1 xn-1 A(x)*B(x) = b 0(a 0 + a 1 x 1 + a 2 x 2 + … an-1 xn-1) + b 1 x(…) + b 2(…) + Example: A(x) = 3 + 2 x – 4 x 2 B(x) = -4 –x + 2 x 2 A(x)*B(x) = 3*(-4) -x(3+2 x- 4 x 2) +2 x 2(3+2 x-4 x 2) Total: O(n 2) scalar multiplications, where n is order of the two polynomials 10/31/2021 FFT 16

Data Structure for Polynomial Coefficient representation (analytical, standard): An = (a 0, a 1, a 2, an-1) Bn = (b 0, b 1, b 3, bn-1) Multiplication: An*Bn = b 0(a 0, a 1, a 2, an-1), b 1(a 0, a 1, a 2, an-1), …, bn(a 0, a 1, a 2, an-1) Coordinate representation (discrete): Evaluate at n points, (x 0, x 1, x 2, xn-1): An = (x 0, y 0), (x 1, y 1), (x 2, y 2), … (xn-1, yn-1), Each evaluation from : O(n) Total: O(n 2) for n points evaluation Why we need n points? 10/31/2021 FFT 17

Data Structure for Polynomial Coordinate representation (discrete): Evaluate at n points, (x 0, x 1, x 2, xn-1): An = (x 0, y 0), (x 1, y 1), (x 2, y 2), … (xn-1, yn-1), Each evaluation from : O(n) Total: O(n 2) for n points evaluation Why we need n points? To recover each coefficient: n unknowns, with n equations y 0 = a 0 + a 1 x 0 + a 2 x 02 + … an-1 x 0 n-1 y 1 = a 0 + a 1 x 1 + a 2 x 12 + … an-1 x 1 n-1…. … yn-1= a 0 + a 1 xn-1 + a 2 xn-12 + … an-1 xn-1 n-1 Complexity of this conversion? 10/31/2021 FFT 18

Polynomial Multiplication Poly-multiplication in coordinate representation: Evaluate at n points: A(x) = 3 + 2 x – 4 x 2 , B(x) = -4 –x + 2 x 2 x=(1, 2, 3) A(1) = 1, A(2)=-9, A(3)=-27 B(1) = -1, B(2)=2, B(3)=11 Multiply point by point: R(1)=-1, R(2)=-18, R(3)=-297, R as resulting polynomial Solve for coefficients of R: linear algebra / simultaneous eq solving 10/31/2021 FFT 19

Polynomial Multiplication Another way: Evaluate at n points: A(x) = 3 + 2 x – 4 x 2 , B(x) = -4 –x + 2 x 2 x=(1, 2, 3) A(1) = 1, A(2)=-9, A(3)=-27 B(1) = -1, B(2)=2, B(3)=11 Multiply point by point: R(1)=-1, R(2)=-18, R(3)=-297, R as resulting polynomial Solve for coefficients of R: linear algebra / simultaneous eq solving How many terms? Coefficients? Order of R? Goes up to 4 th power of x: r 0, r 1, r 2, r 3, r 4 Can be handled by increasing power of A and B with 0 coefficients: A(x) = 3 +2 x -4 x 2 +0 x 3 +0 x 4 +0 x 5 , B(x) = … and evaluating at 6 points, not 3: so that we can recover 6 coefficients 10/31/2021 FFT 20

Polynomial Multiplication by evaluated points Evaluation at each point: O(n) multiplications at x, x 2, x 3, … Evaluation at n points: O(n 2) Multiplication for n points: O(n) Inverse matrix to solve for coefficients: O(n 2) Total poly-mult: O(n 2), no advantage over standard way 10/31/2021 FFT 21

Polynomial Multiplication by evaluated points 10/31/2021 FFT 22

DFT for Polynomial Multiplication (0) Pad each polynomial to (2 n-2)-th order by extending: an=0, an+1=0, . . . , a 2 n-1=0 (1) Evaluate each polynomial at the 2 n-th complex roots of 1: w 2 n 0=1, w 2 n 1=wn, w 2 n 2, w 2 n 3, . . . , w 2 n 2 n-1 (2) Then, element-to-element multiply values at each evaluated pts above: A(wnk)*b(wnk) =: C(wnk), for k=0 … 2 n-1 (3) Find coefficients of resulting polynomial C(x) by using w 0 through w 2 n Steps 1 & 3 each takes O(2 n log 2 n), & Step-2 takes O(2 n) Total O(n logn) 10/31/2021 FFT 23

ωn, n roots of xn=1 ωn =e(i 2π/n) ω 81 ω 80 10/31/2021 FFT 24

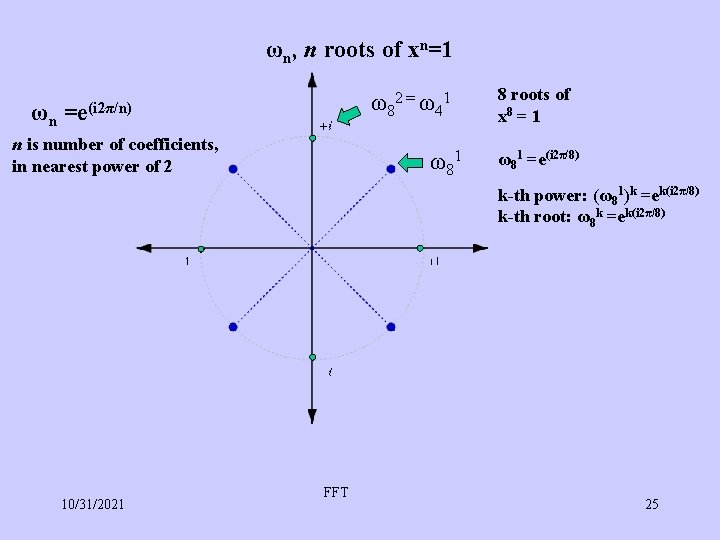
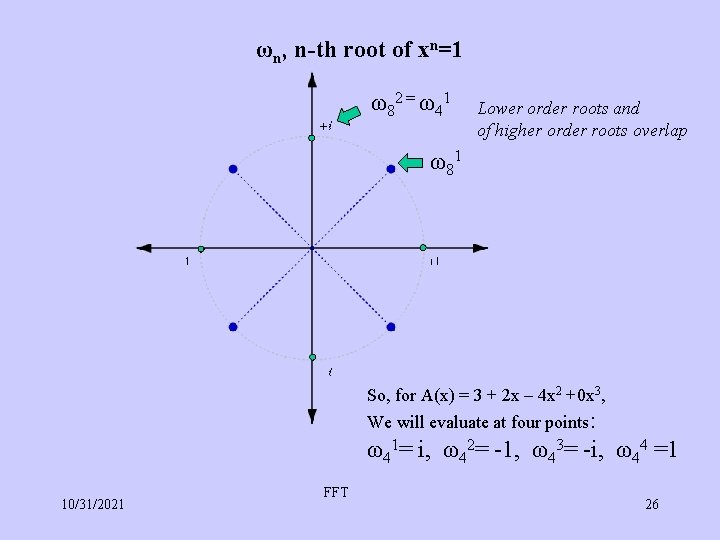
ωn, n roots of xn=1 ω82 = ω41 ωn =e(i 2π/n) n is number of coefficients, in nearest power of 2 ω 81 8 roots of x 8 = 1 ω81 =e(i 2π/8) k-th power: (ω81)k =ek(i 2π/8) k-th root: ω8 k =ek(i 2π/8) 10/31/2021 FFT 25

ωn, n-th root of xn=1 ω82 = ω41 Lower order roots and of higher order roots overlap ω 81 So, for A(x) = 3 + 2 x – 4 x 2 +0 x 3, We will evaluate at four points: ω41= i, ω42= -1, ω43= -i, ω44 =1 10/31/2021 FFT 26

Advantage of using complex roots of one: Divide and Conquer can be faster A(x) = 3 + 2 x – 4 x 2 +0 x 3 , to be evaluated at 4 points ω1 , ω2 , ω3 , ω4 Modulo nature reduces actual number of computations Specifically, rules (theorems/lemmas) used are: ωnn/2 = ω2 = -1 (second root of x 2=1, mid point of roots of any order) ωnn =1 (first root, or 0 -th root of any order) (ωnk+n/2)2 = (ωnk)2 (modulo nature) 8 8 roots of x = 1 ω81 =e(i 2π/8) k-th power: (ω81)k =ek(i 2π/8) k-th root: ω8 k =ek(i 2π/8) 10/31/2021 FFT 27

D&C Polynomial Evaluation A 8(x) = a 0 + a 1 x + a 2 x 2 + a 3 x 3 + a 4 x 4 + a 5 x 5 + a 6 x 6 + a 7 x 7 = (a 0 + a 2 x 2 + a 4 x 4 + a 6 x 6) + x(a 1 + a 3 x 2 + a 5 x 4 + a 7 x 6) = [(a 0 + a 4 x 4) + x 2(a 2 + a 6 x 4)] + x[(a 1 + a 5 x 4) + x 2(a 3 + a 7 x 4)] A polynomial may be written as, A(x) = A 0(x 2) + x. A 1(x 2) where, A 0(z) = a 0 + a 2 z + a 4 z 2 + … + an-2 zn/2 -1 A 1(z) = a 1 + a 3 z + a 5 z 2 + … + an-1 zn/2 -1 Presuming, n = 2 k, the rewriting may recursively go on until k=0. Hence, divide and conquer 10/31/2021 FFT 28

D&C Polynomial Evaluation A 8(x) = a 0 + a 1 x + a 2 x 2 + a 3 x 3 + a 4 x 4 + a 5 x 5 + a 6 x 6 + a 7 x 7 = (a 0 + a 2 x 2 + a 4 x 4 + a 6 x 6) + x(a 1 + a 3 x 2 + a 5 x 4 + a 7 x 6) A 4(x 2) + x A’ 4(x 2) = [(a 0 + a 4 x 4) + x 2(a 2 + a 6 x 4)] + x[(a 1 + a 5 x 4) + x 2(a 3 + a 7 x 4)] A 2((x 2)2) + (x 2)A’ 2((x 2)2) + … Divide and conquer can be now used for evaluating at a value of x. Higher order polynomials from lower order ones, with appropriate coefficients. Now evaluate at all n roots of 1 (DFT): x = ωn 0 through ωnn-1 Fast Fourier Transformation (FFT) combines these computations using modulo properties of roots of 1 10/31/2021 FFT 29

Discrete Fourier Transformation: D&C Polynomial Evaluation T(n) = 2 T(n/2) + n/2 , for the loop (10): O(n) By Master’s theorem: T(n) = O(n log_n) 10/31/2021 FFT 30

Reshuffling of coefficients for recursive calls 10/31/2021 FFT 31

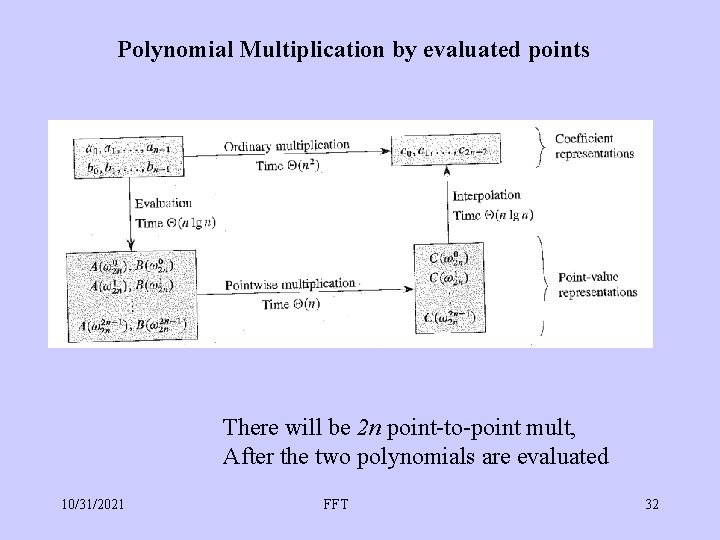
Polynomial Multiplication by evaluated points There will be 2 n point-to-point mult, After the two polynomials are evaluated 10/31/2021 FFT 32

Computing the coefficients from points : interpolation DFT: Y = VA Inverse DFT: Solving simultaneous equations Needs inversion of V matrix: Usually, O(n 2) operation 10/31/2021 FFT 33

Computing the coefficients from points : interpolation ç A polynomial evaluation at ωn-1 Use the same DFT with ωn-1 O(n logn) 10/31/2021 FFT 34

Computing the coefficients from points : interpolation Solving simultaneous equations to find coefficients vector A: A = V-1 Y: but V-1 kj = 1/(n* Vjk) Use ωn =e(-i 2π/n) in line 4 of DFT, and divide the final returned vector by n 10/31/2021 FFT 35

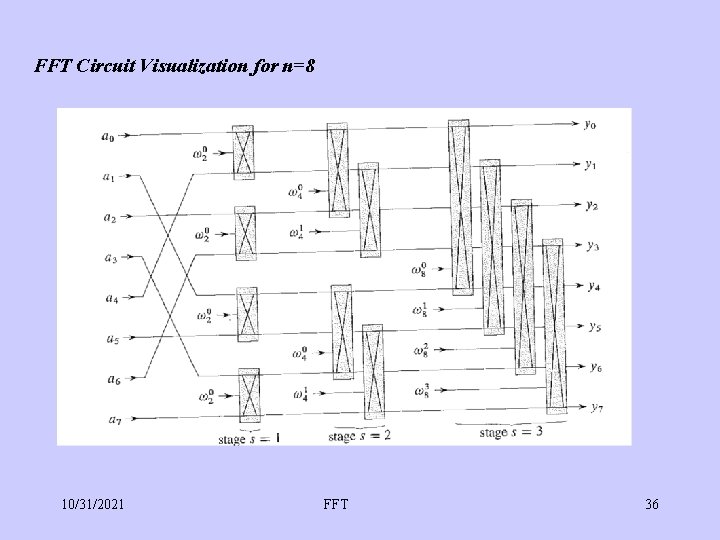
FFT Circuit Visualization for n=8 10/31/2021 FFT 36

Fast Fourier Transform: FFT: Iterative version of DFT BIT-REVERSE-COPY: shuffle input vector 10/31/2021 FFT 37

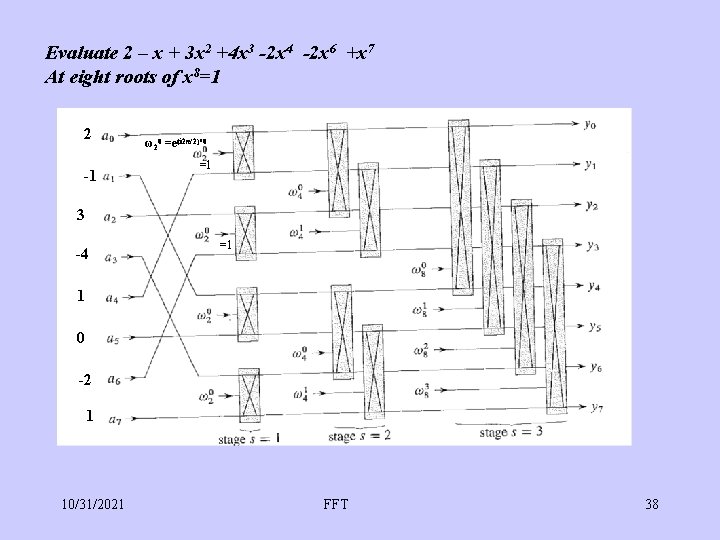
Evaluate 2 – x + 3 x 2 +4 x 3 -2 x 4 -2 x 6 +x 7 At eight roots of x 8=1 2 -1 ω20 =e(i 2π/2)*0 =1 3 -4 =1 1 0 -2 1 10/31/2021 FFT 38

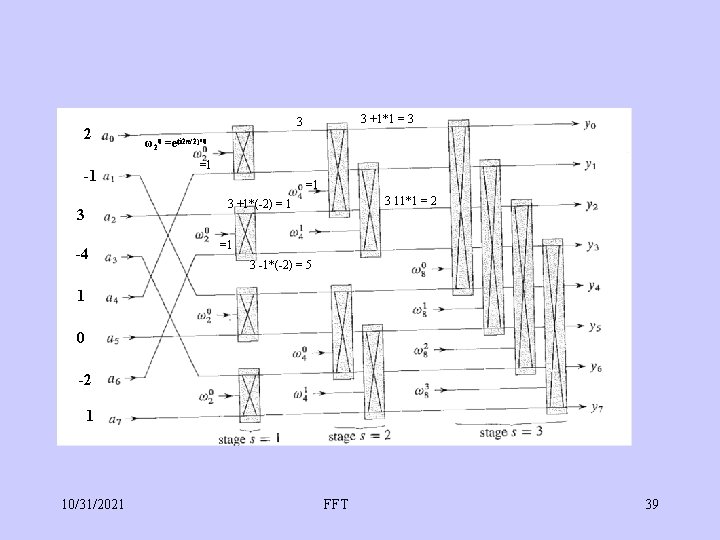
2 -1 3 +1*1 = 3 3 ω20 =e(i 2π/2)*0 =1 =1 3 11*1 = 2 3 +1*(-2) = 1 3 -4 =1 3 -1*(-2) = 5 1 0 -2 1 10/31/2021 FFT 39

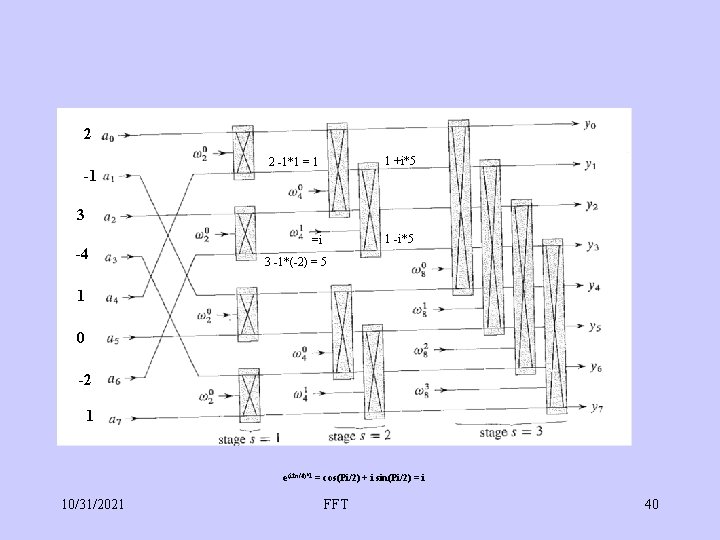
2 -1*1 = 1 1 +i*5 =i 1 -i*5 3 -4 3 -1*(-2) = 5 1 0 -2 1 e(i 2π/4)*1 = cos(Pi/2) + i sin(Pi/2) = i 10/31/2021 FFT 40

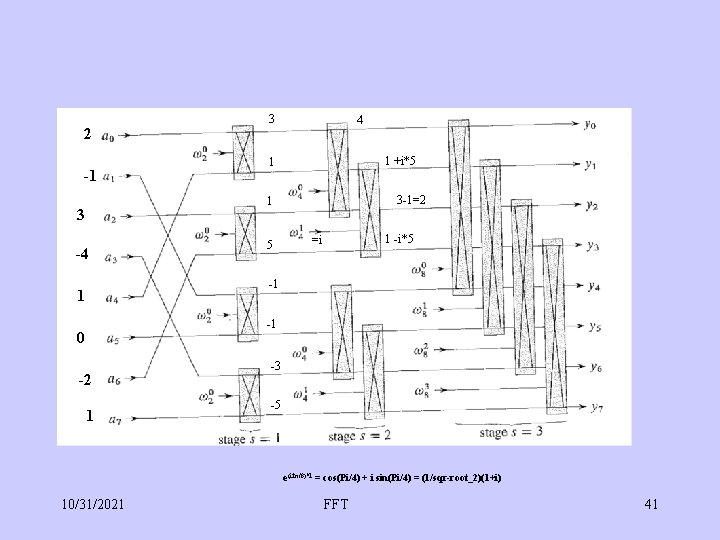
2 -1 3 4 1 +i*5 1 3 -1=2 1 3 -4 5 1 -i*5 =i -1 1 -1 0 -2 1 -3 -5 e(i 2π/8)*1 = cos(Pi/4) + i sin(Pi/4) = (1/sqr-root_2)(1+i) 10/31/2021 FFT 41