polynomial function degree coefficient a n lead undefined






















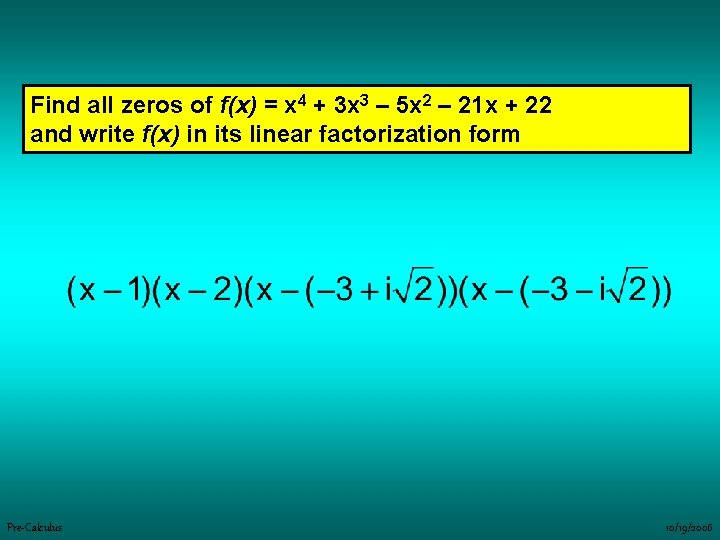

- Slides: 25

polynomial function degree coefficient a n lead undefined zero function f(x) = 0 constant function f(x) = 5 0 linear function f(x) = 2 x + 5 1 quadratic function f(x) = x 2 + 2 x + 5 2 slope Pre-Calculus linear constant non-zero 10/19/2006

roots or solutions x = -1 or 3. 5 vertex: (h, k) complete the square vertex: (– 4, – 1) axis of symmetry: x = – 4 Pre-Calculus 10/19/2006

vertex: (1, 5) x – intercepts: Pre-Calculus vertex: 10/19/2006

power varies as constant of variation or proportion is proportional to power function power: – 4 constant of variation: 2 not a power function: power isn’t a constant power function independent variable: r power: 2 constant of variation: power is 1, constant of variation is 2 power is 2, constant of variation is 1 direct variation Pre-Calculus 10/19/2006

d=k. F d=kt 2 non-negative integer monomial degree: 0 lead coefficient: 4 not monomial power is ½ (not an integer) Pre-Calculus monomial degree: 3 lead coefficient: 13 not monomial power is a variable 10/19/2006

vertical stretch / shrink reflection across the x-axis domain range continuity increasing decreasing symmetry boundedness extrema asymptotes end behavior Pre-Calculus 10/19/2006

dividend quotient Pre-Calculus divisor remainder 10/19/2006

k=3 k = – 2 k=5 (3)2 – 4(3) – 5 = 9 – 12 – 5 = – 8 (– 2)2 – 4(– 2) – 5 = 4 + 8 – 5 = 7 (5)2 – 4(5) – 5 = 25 – 20 – 5 = 0 divides evenly zero x - intercept solution Pre-Calculus root 10/19/2006

so factors are: x + 4, x – 3, x + 1 3(x + 4)(x – 3)(x + 1) = 3 x 3 + 6 x 2 – 33 x – 36 so factors are: x + 3, x + 2, x – 5 2(x + 3)(x + 2)(x – 5) = 2 x 3 – 38 x – 60 Pre-Calculus 10/19/2006

f(x) = x 2 – 16 (x + 4)(x – 4) = 0 x = 4, x = – 4 rational zeros Pre-Calculus 10/19/2006

Use the rational zeros theorem to find the rational zeros of f(x) = 2 x 3 + 3 x 2 – 8 x + 3 p = integer factors of the constant q = integer factors of the lead coefficient potential: Pre-Calculus 10/19/2006

Pre-Calculus 10/19/2006

complex (real and non-real) zeros * non-real zeros are not x – intercepts zeros: 3 i, – 5 x-intercepts: – 5 complex conjugate (a + bi and a – bi) Pre-Calculus 10/19/2006

x 4 – 14 x 3 + 78 x 2 – 206 x + 221 Pre-Calculus 10/19/2006

denominator the x – axis ( y = 0 ) the line y = an / bm there is no quotient output input Pre-Calculus 10/19/2006

vertical asymptote: x – intercept none horizontal asymptote: y – intercept y=0 (0, 4) vertical asymptote: x – intercept x = – 1 horizontal asymptote: none (0, 0) (1, 0) y – intercept (0, 0) slant asymptote: y = x – 2 Pre-Calculus 10/19/2006

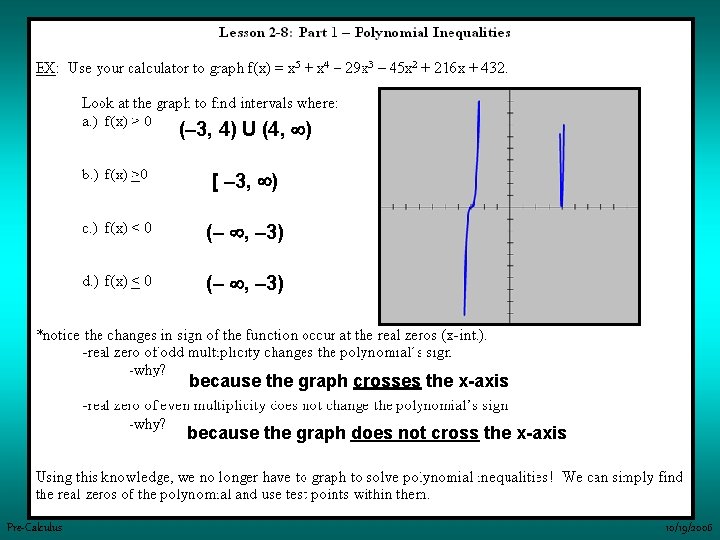
(– 3, 4) U (4, ) [ – 3, ) (– , – 3) because the graph crosses the x-axis because the graph does not cross the x-axis Pre-Calculus 10/19/2006

1, – 3, 2 + – – 3 + + 1 2 (– , – 3) U (1, 2) U (2, ) (– 3, 1) Pre-Calculus 10/19/2006

Write a standard form polynomial function of degree 4 whose zeros include 1 + 2 i and 3 – i. Pre-Calculus quiz 10/19/2006

Solve the following inequality using a sign chart: x 3 + 2 x 2 – 11 x – 12 < 0 Pre-Calculus quiz 10/19/2006

Write the following polynomial function in standard form. Then identify the zeros and the x – intercepts. f(x) = (x – 3 i) (x + 4) zeros: x – intercepts: Pre-Calculus quiz 10/19/2006

Without graphing, using a sign chart, find the values of x that cause f(x) = (x – 2) (x + 6) (x + 1) to be: a. ) zero ( f(x) = 0 ) b. ) positive ( f(x) > 0 ) c. ) negative ( f(x) < 0 ) a. ) 2, – 1 , – 6 b. ) (– 6, – 1) U (2, ) c. ) (– , – 6) U (-1, 2) Pre-Calculus quiz 10/19/2006

Use the quadratic equation to find the zeros of f(x) = 5 x 2 – 2 x + 5. Your answer must be in exact simplified form. Pre-Calculus quiz 10/19/2006
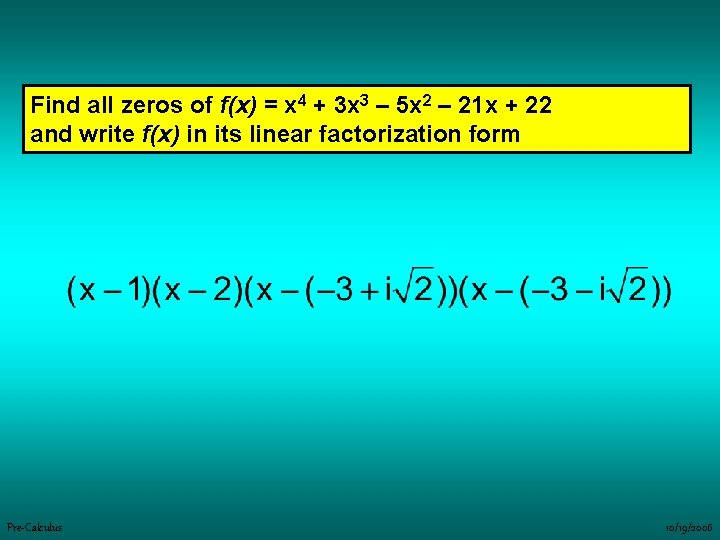
Find all zeros of f(x) = x 4 + 3 x 3 – 5 x 2 – 21 x + 22 and write f(x) in its linear factorization form Pre-Calculus 10/19/2006

2 i is a zero of f(x) = 2 x 4 – x 3 + 7 x 2 – 4 x – 4. Find all remaining zeros and write f(x) in its linear factorization form. Pre-Calculus quiz 10/19/2006