Polynomial and Rational Functions Lesson 2 3 Animated

Polynomial and Rational Functions Lesson 2. 3

Animated Cartoons Note how mathematics are referenced in the creation of cartoons

Animated Cartoons We need a way to take a number of points and make a smooth curve This lesson studies polynomials

Polynomials General polynomial formula • a 0, a 1, … , an are constant coefficients • n is the degree of the polynomial • Standard form is for descending powers of x • anxn is said to be the “leading term” Note that each term is a power function

Family of Polynomials Constant polynomial functions • f(x) = a Linear polynomial functions • f(x) = m x + b Quadratic polynomial functions • f(x) = a x 2 + b x + c

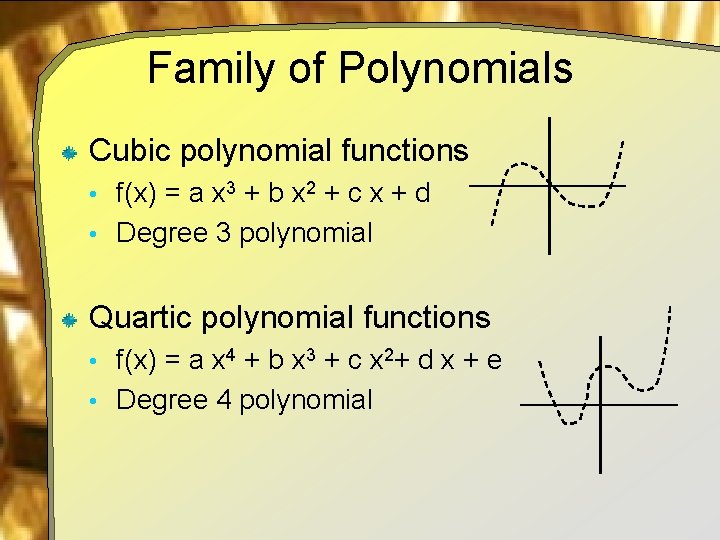
Family of Polynomials Cubic polynomial functions • f(x) = a x 3 + b x 2 + c x + d • Degree 3 polynomial Quartic polynomial functions • f(x) = a x 4 + b x 3 + c x 2+ d x + e • Degree 4 polynomial

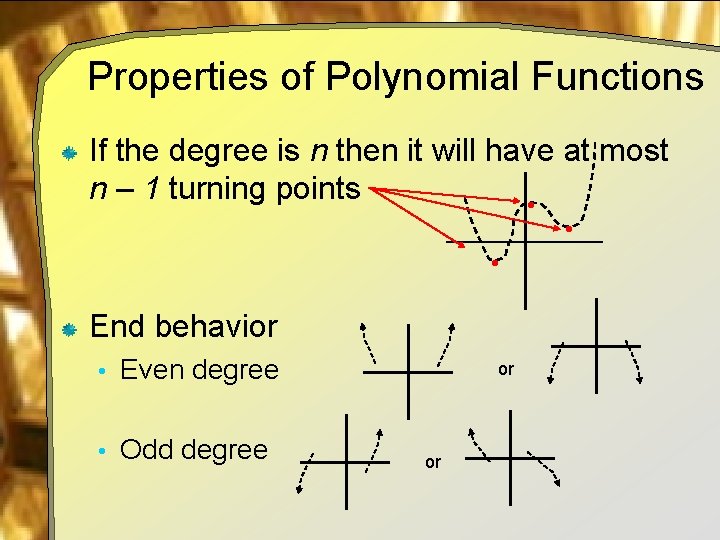
Properties of Polynomial Functions If the degree is n then it will have at most n – 1 turning points • • • End behavior • Even degree • Odd degree or or

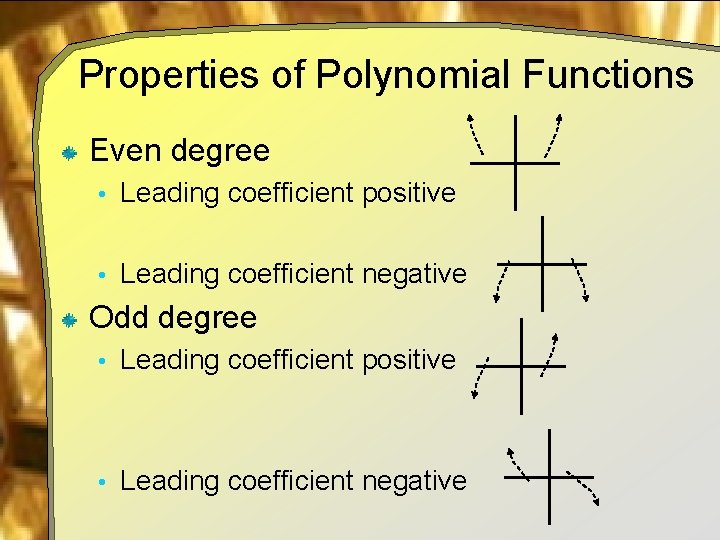
Properties of Polynomial Functions Even degree • Leading coefficient positive • Leading coefficient negative Odd degree • Leading coefficient positive • Leading coefficient negative

Rational Function: Definition Consider a function which is the quotient of two polynomials Both polynomials Example:

Long Run Behavior Given The long run (end) behavior is determined by the quotient of the leading terms • Leading term dominates for large values of x for polynomial • Leading terms dominate for the quotient for extreme x

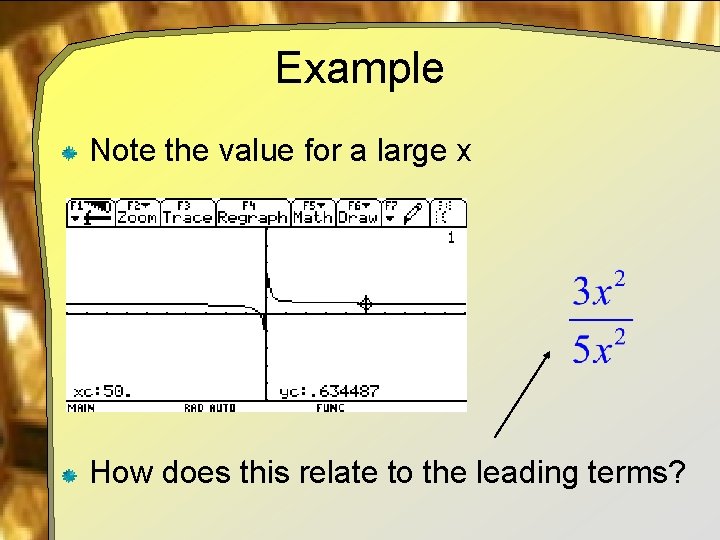
Example Given Graph on calculator • Set window for -100 < x < 100, -5 < y < 5

Example Note the value for a large x How does this relate to the leading terms?

Try This One Consider Which terms dominate as x gets large What happens to as x gets large? Note: • Degree of denominator > degree numerator • Previous example they were equal

When Numerator Has Larger Degree Try As x gets large, r(x) also gets large But it is asymptotic to the line

Summarize Given a rational function with leading terms When m = n • Horizontal asymptote at When m > n • Horizontal asymptote at 0 When n – m = 1 • Diagonal asymptote

Vertical Asymptotes A vertical asymptote happens when the function R(x) is not defined • This happens when the denominator is zero Thus we look for the roots of the denominator Where does this happen for r(x)?

Vertical Asymptotes Finding the roots of the denominator View the graph to verify

Assignment Lesson 2. 3 Page 91 Exercises 3 – 59 EOO