Polynome und schnelle Fourier Transformation Mohsen Taheri FU





























- Slides: 30

Polynome und schnelle Fourier. Transformation Mohsen Taheri FU Berlin – So. Se 2012

Polynome � Ein Polynom ist eine Funktion � Koeffizienten: � Ein Polynom hat Grad k wenn der höchste Koeffizient mit einem Wert ungleich 0 � Länge = jede ganze Zahl großer als Grad eines Polynoms 2 Polynome und FFT

Addition von Polynomen � Seien und � Polynome � Addition � hat der Länge n von A(x) und B(x) ist auch Länge n � und � Beispiel � Laufzeit: 3 Polynome und FFT

Multiplikation von Polynomen � Seien und � Polynome der Länge n � Multiplikation von A(x) und B(x) ist � Wobei � Länge(C) = Länge(A) + Länge(B) � Beispiel � Laufzeit: 4 Polynome und FFT

Darstellung von Polynomen � Koeffizienten-Darstellung � Point-Value-Darstellung 5 Polynome und FFT

Koeffizienten-Darstellung � Das Polynom Koeffizienten � als ein Vektor der Addition: � Laufzeit � Multiplikation � (wie vorhin): wobei � Laufzeit 6 Polynome und FFT

Point-Value-Darstellung � Polynom Länge n in Point-Value- Darstellung: � eine Menge von Punkten � alle sind disjunkt � für alle : � Auswertung 7 durch Horne-Schema (in Polynome und FFT )

Addition in Point-Value-Darstellung �A : �B : � Addition: � Laufzeit: 8 Polynome und FFT

Multiplikation in Point-Value-Darstellung � Problem: Länge(A. B)=Länge(A)+Länge(B) � Lösung: Extended Point-Value � 2 n Punkte statt n Punkte � A: � B: � Multiplikation: � C: � Laufzeit 9 : Polynome und FFT

Evaluation � Evaluation: Transform von Koeffizienten-Vektor zur Point-Value-Darstellung � Evaluating: Die Auswertung eines Polynoms unter einen bestimmten Wert von x � Mit Hilfe von Horne-Schema in � Evaluation 10 insgesamt in Polynome und FFT

Interpolation � Interpolation: Transform von Point-Value. Darstellung zur Koeffizienten-Darstellung � Lagranges Formel 11 Polynome und FFT

Theorem 1: Eindeutigkeit von Interpolation der Polynomen � Für alle Menge von n Punkten � mit disjunkt � gibt es eindeutiges Polynom A(x) der Länge n, so dass � für alle � 12 Polynome und FFT

DFT � effiziente Methode für Evaluation und Interpolation � Diskrete Fourier Transform � Das Polynom Einheitswurzeln auswerten in n komplexe n-te � � Eingabe: Koeffizienten-Vektor � Ausgabe: Vektor � Auswertung der Polynom in n Komplexe n-te Einheitswurzeln 13 Polynome und FFT

Komplexe Einheitswurzeln � komplexe Einheitswurzel: eine komplexe Zahl � wobei � Es gibt genau n komplexe n-te Einheitswurzeln: � für � Die k=0, 1, … , n-1: Zahl � alle �n 14 : primitive n-te Einheitswurzel anderen Zahlen sind die Potenzen dieser Zahl komplexe n-te Einheitswurzeln sind dann: Polynome und FFT

Komplexe Einheitswurzeln - Eigenschaften � Additive � Die Gruppe n Zahlen Struktur wie die additive Gruppe � Beweis: 15 haben die gleiche Polynome und FFT

Komplexe Einheitswurzeln - Eigenschaften � Cancellation Lemma � Für jede ganze Zahl � Beweis: gilt: . � Korollar: � Für 16 alle ganze Zahlen n>0 gilt: Polynome und FFT

Komplexe Einheitswurzeln - Eigenschaften � Halving Lemma: � wenn n>0 gerade Zahl � die Quadrate der n komplexen n -te Einheitswurzeln sind die n/2 komplexe (n/2)-te Einheitswurzeln: 17 Polynome und FFT

Komplexe Einheitswurzeln - Eigenschaften � Halving Lemma: � Beweis: Da n gerade ist, nehmen wir an n=2 m � Zu zeigen: � Nach Cancellation Lemma: � da , ist dann , also □ 18 Polynome und FFT

Komplexe Einheitswurzeln - Eigenschaften � Summation Lemma: � Für jede ganze Zahl n≥ 1 und für k≠ 0 und nicht dividierbar durch n, gilt: 19 Polynome und FFT

FFT � Evaluation � unter eines Polynoms in Verwendung der Eigenschaften der Einheitswurzeln � Diese Methode heißt Fast Fourier Transform(FFT). � Annahme n ist ein 2 er Potenz ( ) � Divide-and-Conquer 20 Polynome und FFT

FFT � das Polynom A(x) in gerade und ungerade indizierte Koeffizienten teilen � zwei neue Polynome der Länge n/2 � Das 21 Polynom wird so berechnet: Polynome und FFT

FFT � das Problem von Auswerten des Polynoms in n Punkten ( ) reduziert zu: � 1. zwei Polynome Punkten ( der Länge n/2 in ) auswerten � 2. das Resultat mit Hilfe der Abgleichung zusammen addieren 22 Polynome und FFT

FFT � Nach Halving Lemma: � die Anzahl der Elemente der Liste nicht n, sondern n/2. � Die zwei Subprobleme haben genau die gleiche Struktur wie das ursprüngliche Problem und sind halb so groß. 23 Polynome und FFT

Rekursiv FFT RECURSIVE-FFT(a) 1. n = a. length() 2. if n==1 3. return a Eingabe: Ausgabe: 4. 5. 6. 7. 8. 9. 10. for k=0 to n/2 -1 11. 12. 13. 14. 24 return y Polynome und FFT

Rekursiv FFT � Zeilen 11 -12 kombinieren das Ergebnis der rekursiven Berechnung � Zeile 11 für � Zeile 12 für � zusammengefügt 25 wird Vektor y berechnet Polynome und FFT

Rekursiv FFT - Laufzeit � jeder rekursiver Aufruf kostet � n = Länge des Eingabevektors � Laufzeit: 26 Polynome und FFT

Interpolation in Einheitswurzeln � umgekehrtes � Polynom Verfahren vom Point-Value zurück zu Koeffizienten � Berechnung von DTF als eine Matrizenmultiplikation � Vandermonde-Matrix � wir 27 brauchen die Inverse-Matrix Polynome und FFT

Inverse von Vandermonde-Matrix � Theorem: Für j, k=0, 1, …, n-1 sind die (j, k)Einträge von die Zahlen � Beweis: � z. z. : , wobei die n×n Identitätsmatrix � betrachte die (j, j')Einträge von � Falls j=j‘ : j≠j‘ : � -(n-1) ≤ j-j' ≤ n-1 j-j' ist nicht durch n dividierbar � Summation Lemma : 28 Polynome und FFT

Interpolation in Einheitswurzeln : (j, k)Einträge der � II : �I � Vergleiche sind: mit Polynom in Einheitswurzeln � leichte Modifikation in Algorithmus berechnet die Interpolation � tausche a und y � ersetze durch � dividiere jedes Element durch n � Also 29 die Interpolation auch in berechenbar Polynome und FFT

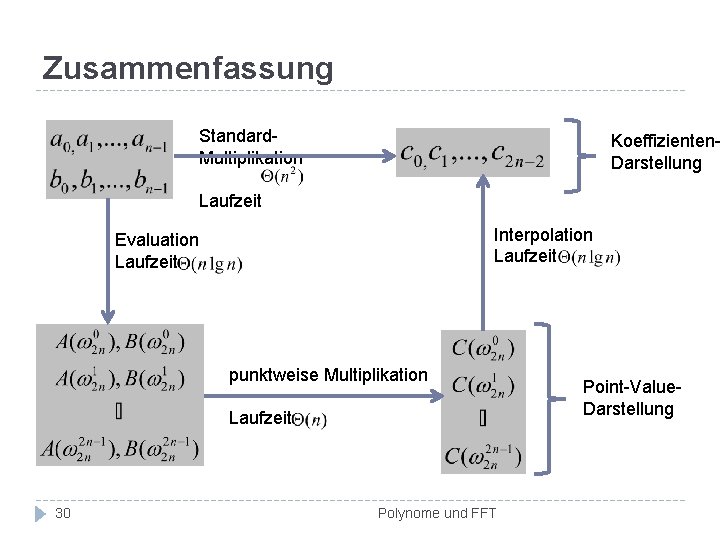
Zusammenfassung Standard. Multiplikation Koeffizienten. Darstellung Laufzeit Interpolation Laufzeit Evaluation Laufzeit punktweise Multiplikation Laufzeit 30 Polynome und FFT Point-Value. Darstellung
 Koeffizient mathe
Koeffizient mathe Monome constant
Monome constant Polynome faktorisieren
Polynome faktorisieren Polynome caractéristique
Polynome caractéristique Mohsen sadatsafavi
Mohsen sadatsafavi Mohsen ghaffari
Mohsen ghaffari Mohsen khakzad
Mohsen khakzad Mohsen kahani
Mohsen kahani Dr ala mohsen
Dr ala mohsen Ashraf game
Ashraf game Mohsen beheshti
Mohsen beheshti Mohsen amini salehi
Mohsen amini salehi Mohsen eskala
Mohsen eskala Saad mohsen ٨- احذر احذر
Saad mohsen ٨- احذر احذر Engineering research methods
Engineering research methods Mohsen afsharchi
Mohsen afsharchi Transformata laplace calculator
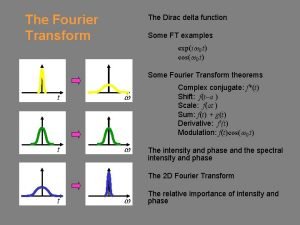
Transformata laplace calculator Linearity property of fourier transform
Linearity property of fourier transform Fourier transform of the dirac delta function
Fourier transform of the dirac delta function Fourier series pairs
Fourier series pairs Fourier sor
Fourier sor Função par e impar
Função par e impar Fast fourier
Fast fourier Ley de fourier
Ley de fourier R fft
R fft Transformée de fourier cosinus
Transformée de fourier cosinus Fourier image processing
Fourier image processing Fourier transform spherical coordinates
Fourier transform spherical coordinates Aperiodic signal
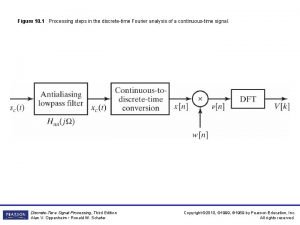
Aperiodic signal Fourier analysis of discrete time signals
Fourier analysis of discrete time signals Half range cosine series
Half range cosine series