Polyhedron A 3 dimensional object formed by polygonal

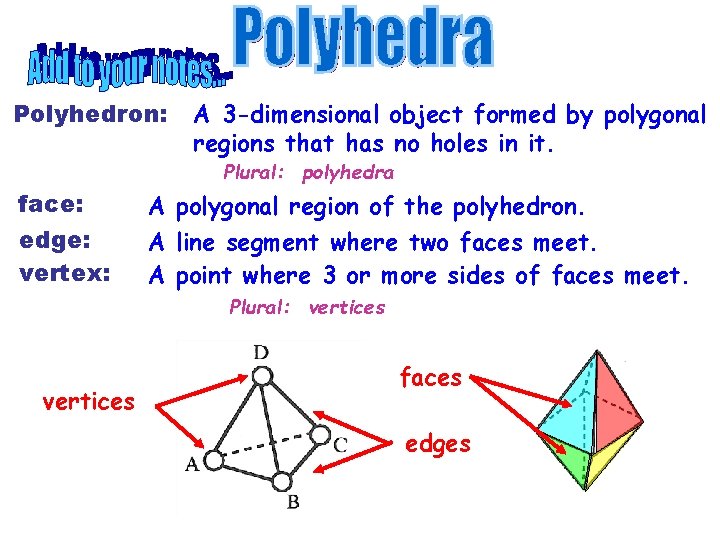
Polyhedron: A 3 -dimensional object formed by polygonal regions that has no holes in it. Plural: polyhedra face: edge: vertex: A polygonal region of the polyhedron. A line segment where two faces meet. A point where 3 or more sides of faces meet. Plural: vertices faces edges

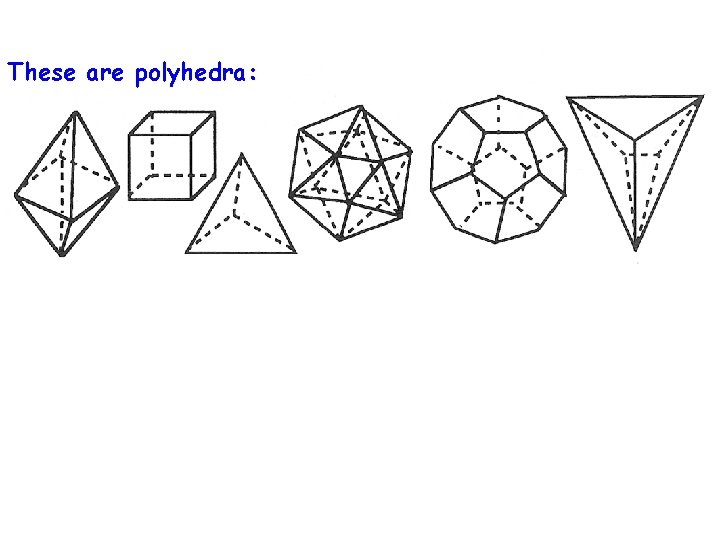
These are polyhedra: These are NOT polyhedra:

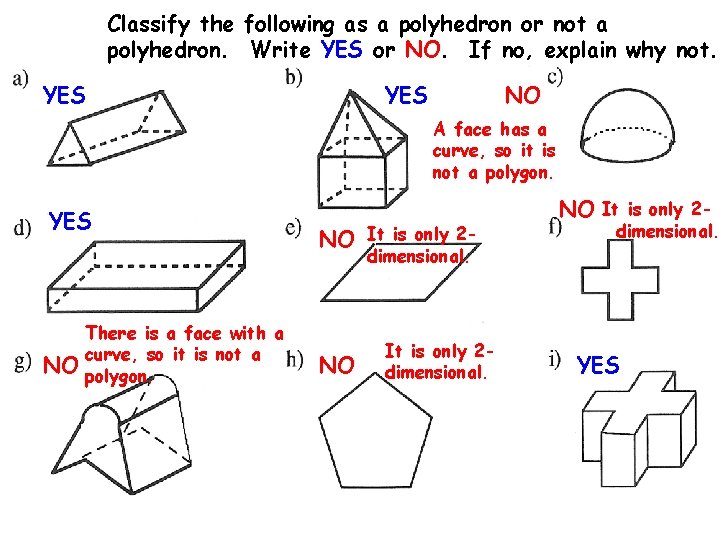
Classify the following as a polyhedron or not a polyhedron. Write YES or NO. If no, explain why not. YES NO A face has a curve, so it is not a polygon. YES NO It is only 2 dimensional. NO There is a face with a curve, so it is not a polygon. NO It is only 2 dimensional. NO It is only 2 - dimensional. YES

Polyhedra are classified by the number of faces they have. Here are some of their names: 4 faces tetrahedron 9 faces nonahedron 5 faces pentahedron 10 faces decahedron 6 faces hexahedron 11 faces undecahedron 7 faces heptahedron 12 faces dodecahedron 8 faces octahedron 20 faces icosahedron Be familiar with these names.

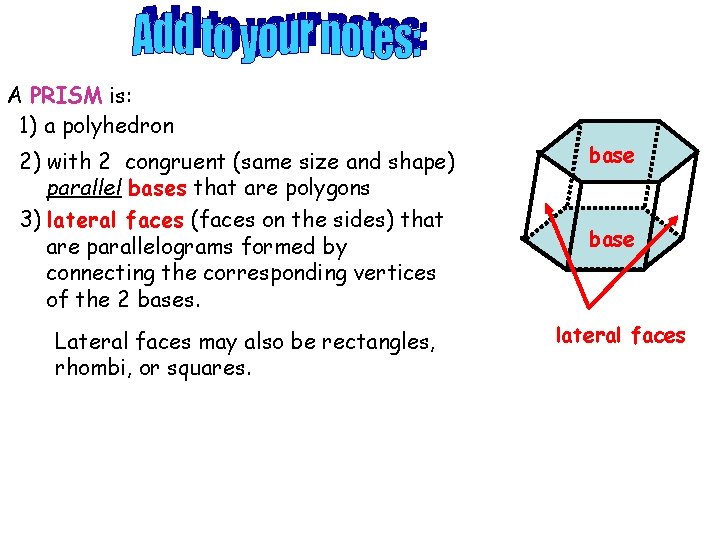
A PRISM is: 1) a polyhedron 2) with 2 congruent (same size and shape) parallel bases that are polygons 3) lateral faces (faces on the sides) that are parallelograms formed by connecting the corresponding vertices of the 2 bases. Lateral faces may also be rectangles, rhombi, or squares. base lateral faces

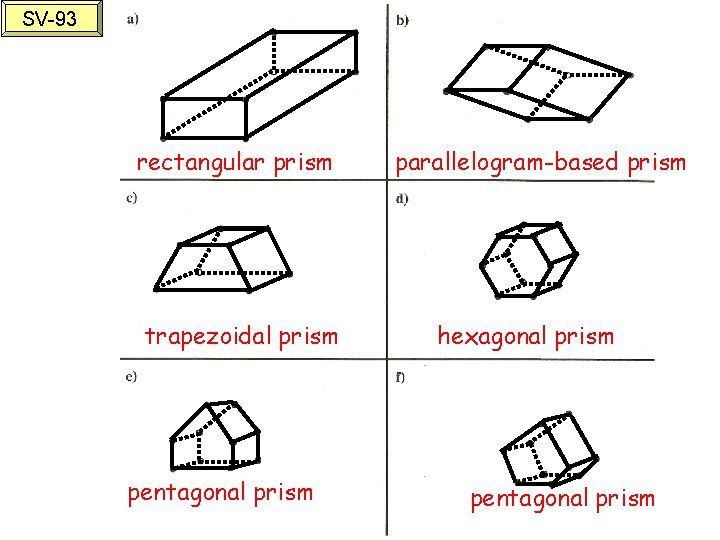
SV-93 rectangular prism trapezoidal prism pentagonal prism parallelogram-based prism hexagonal prism pentagonal prism

Total Surface Area: The sum of the areas of EACH of the faces of a polyhedron. We can set up TSA problems just like we do area subproblems! One equation…four steps: 1. Picture Equation 2. Formulas 3. Simplify 4. Solve & Answer with correct units. What type of units would be correct for Total Surface Area? units 2

Since the base of a prism remains constant (if we slice it parallel to the base, we will have a stack of “bases” that are exactly the height same), we can use this information to find its VOLUME. Volume: The amount of space that an object occupies 3 dimensional (units 3) Volume of a prism: V = (base area) ● height V = BA h *answers expressed in cubic units (u 3) You will draw a PICTURE EQUATION so that it is evident what you are using as your base.

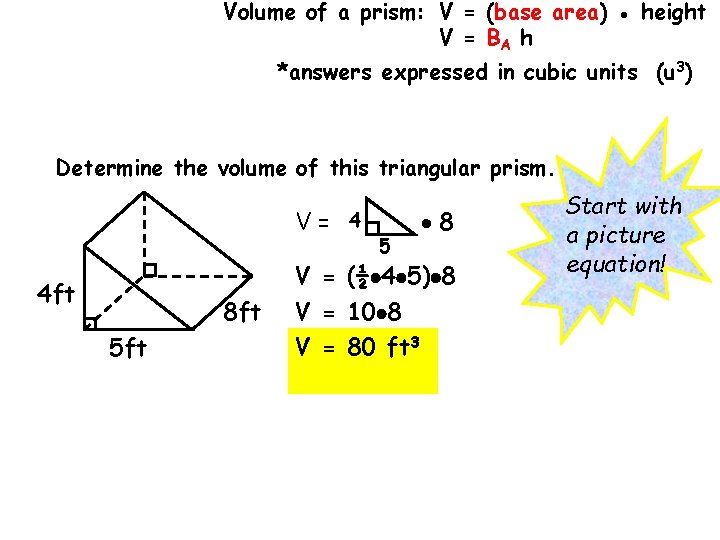
Volume of a prism: V = (base area) ● height V = BA h *answers expressed in cubic units (u 3) Determine the volume of this triangular prism. V= 4 ft 8 ft 5 ft 4 5 8 V = (½ 4 5) 8 V = 10 8 V = 80 ft 3 Start with a picture equation!

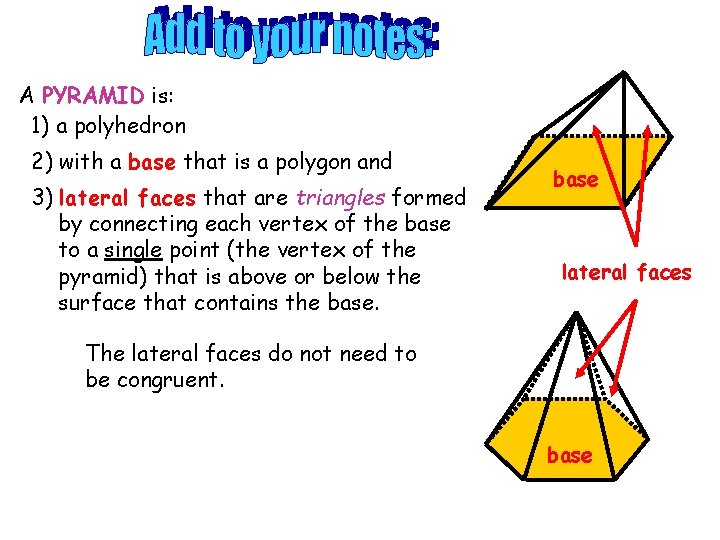
A PYRAMID is: 1) a polyhedron 2) with a base that is a polygon and 3) lateral faces that are triangles formed by connecting each vertex of the base to a single point (the vertex of the pyramid) that is above or below the surface that contains the base lateral faces The lateral faces do not need to be congruent. base

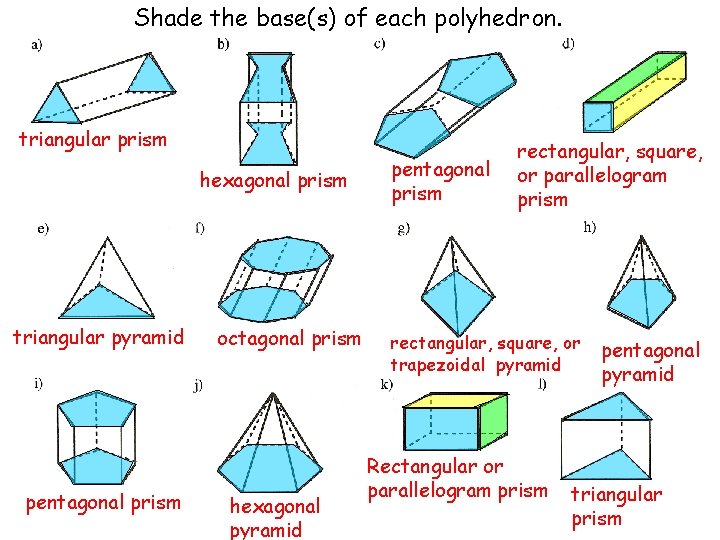
Shade the base(s) of each polyhedron. triangular prism hexagonal prism triangular pyramid pentagonal prism octagonal prism hexagonal pyramid pentagonal prism rectangular, square, or parallelogram prism rectangular, square, or trapezoidal pyramid Rectangular or parallelogram prism pentagonal pyramid triangular prism