Polygons A Polygon is a closed plane figure















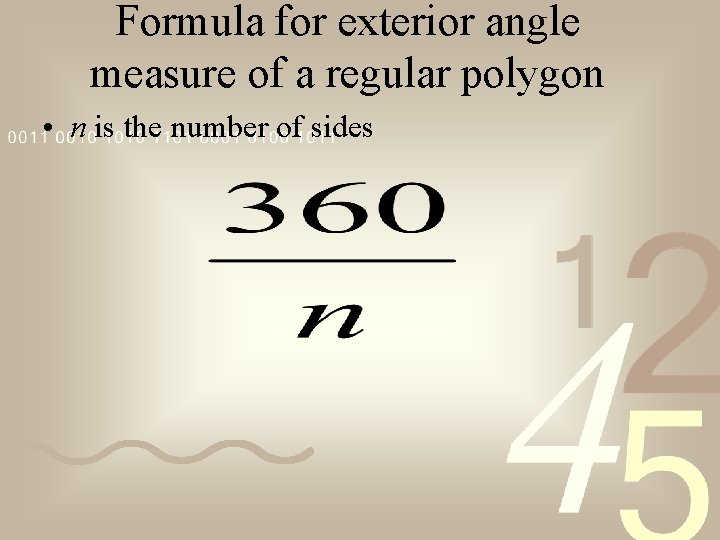




- Slides: 20

Polygons A Polygon is a closed plane figure formed by 3 or more segments Each segment intersects exactly 2 other segments only at their endpoints. No 2 segments with a common endpoint are collinear

Sides • The segments that form a polygon are called its sides. • In a polygon, no 2 segments with a common endpoint are collinear

Vertex of a Polygon • The vertex of a polygon is the intersection of 2 of its sides.

EQUIANGULAR POLYGON • An equiangular polygon is a polygon in which all angles are congruent

Equilateral Polygon • An equilateral polygon is a polygon in which all sides are congruent.

REGULAR POLYGON • If a polygon is both equiangular and equilateral, then it is called regular.

Irregular Polygon • If a polygon is not equiangular and equilateral, then it is an irregular polygon

Polygons named by number of sides 11 sided polygon - hendecagon

Diagonal of a polygon • A diagonal of a polygon is a segment that connects 2 nonconsecutive vertices.

Convex polygon • In a convex polygon, every diagonal lies inside it

Concave polygon • In a concave polygon, at least 1 diagonal can be drawn so that part of it contains points in the exterior of the polygon

Congruent polygons • If 2 polygons have the same size and shape, they are congruent

Interior and Exterior angles of polygons • At each vertex, there are 2 special angles. • An interior angle is an angle fprmed by 2 sides of a polygon with a common vertex • An exterior angles is an angle formed by 1 side of a polygon and the extension of an adjacent side E I

Formula for sum of interior angles of a polygon • n is the number of sides sum of interior angles = (n-2) o 180

Formula for interior angles measure of a regular polygon • n is the number of sides • Each interior angle =
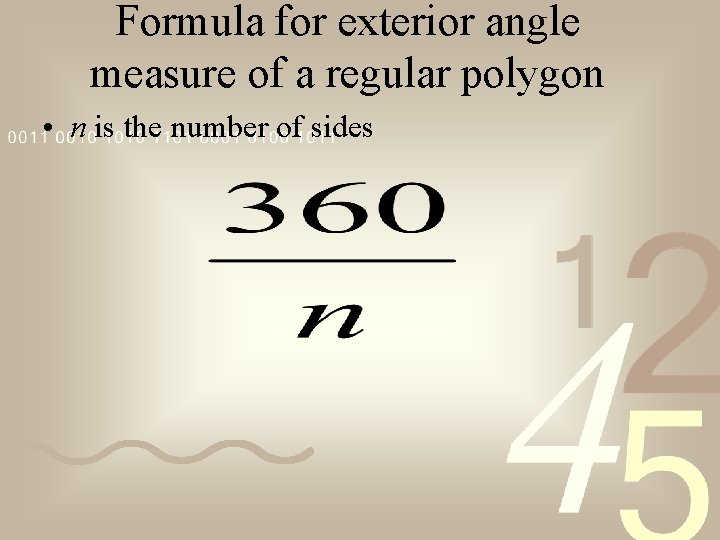
Formula for exterior angle measure of a regular polygon • n is the number of sides

Center of a regular polygon • Center is the point that is equidistant from each of the polygon's vertices

Central angle of a regular polygon • Central angle has its vertex at the center of the polygon and its sides pass through consecutive vertices

Formula for central angle measure of a regular polygon • n is the number of sides
