POLYGONS 6 3 2 3 Develop and use

• • • I can… Classify polygons by their sides Deconstruct polygons into

Polygon A polygon is a closed figure made by three or more segments called

Q: Is this a polygon? Why or why not? A: No… Polygons are closed

Q: Is this a polygon? Why or why not? A: No… It is not

Q: Is this a polygon? Why or why not? A: No… Its sides do

Regular Polygons A regular polygon is a polygon whose sides are all the same

Vertex of a Polygon • The vertices of a polygon are the points where

Triangle A three-sided polygon. The sum of the angles of a triangle is 180

Quadrilateral A four-sided polygon. The sum of the angles of a quadrilateral is 360

Pentagon A five-sided polygon. The sum of the angles of a pentagon is 540

Hexagon A six-sided polygon. The sum of the angles of a hexagon is 720

Heptagon A seven-sided polygon. The sum of the angles of a heptagon is 900

Octagon An eight-sided polygon. The sum of the angles of an octagon is 1080

Nonagon A nine-sided polygon. The sum of the angles of a nonagon is 1260

Decagon A ten-sided polygon. The sum of the angles of a decagon is 1440

Diagonals of a Regular Polygon How many diagonals can be drawn from one vertex

Diagonals of a Regular Polygon You can also multiply the number of triangles inside

Interior Angles of Polygons In an n-sided polygon in which the measure of each

Interior Angles of Polygons (n – 2) • 180 o o (8 – 2)

Find the unknown angles below. w 70 o x 100 o 75 o (4

An exterior angle of a regular polygon is formed by extending one side of

Polygons 9. 6 Notes v closed figure made by three or more segments called

Slides: 27

Download presentation

POLYGONS 6. 3. 2. 3 Develop and use formulas for the sums of the interior angles of polygons by decomposing into triangles.

• • • I can… Classify polygons by their sides Deconstruct polygons into triangles to determine the sum of the interior angles Determine missing exterior angles of a polygon Self Assessment 5 - I can do it without help & teach others. 4 - I can do this with no help, but I don’t know if I can explain it. 3 - I can do this with a little help. 2 - I can do this with a lot of help! 1 - I don’t have a clue.

Polygon A polygon is a closed figure made by three or more segments called sides. Each side intersects exactly two other sides.

Q: Is this a polygon? Why or why not? A: No… Polygons are closed figures.

Q: Is this a polygon? Why or why not? A: No… It is not made of line segments.

Q: Is this a polygon? Why or why not? A: No… Its sides do not intersect in exactly two places each.

Regular Polygons A regular polygon is a polygon whose sides are all the same length, and whose angles are all the same.

Vertex of a Polygon • The vertices of a polygon are the points where its sides intersect.

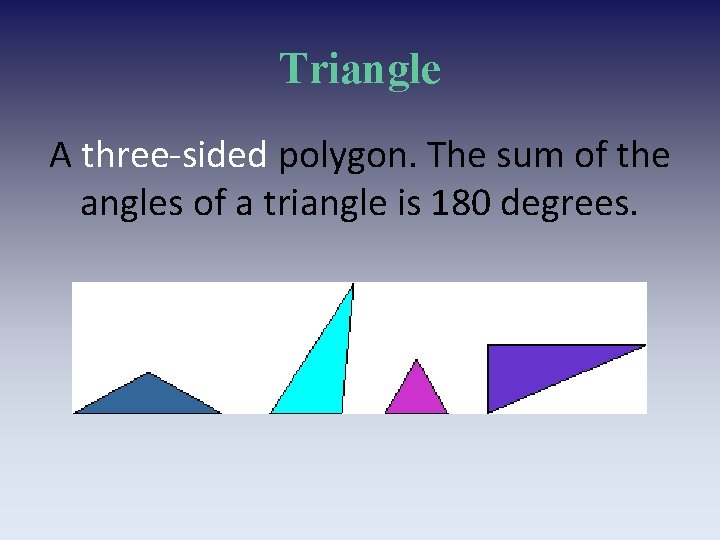
Triangle A three-sided polygon. The sum of the angles of a triangle is 180 degrees.

Quadrilateral A four-sided polygon. The sum of the angles of a quadrilateral is 360 degrees.

Pentagon A five-sided polygon. The sum of the angles of a pentagon is 540 degrees. A regular pentagon: An irregular pentagon: Regular Polygon: All sides are equal and all angles are the same

Hexagon A six-sided polygon. The sum of the angles of a hexagon is 720 degrees. A regular hexagon: An irregular hexagon:

Heptagon A seven-sided polygon. The sum of the angles of a heptagon is 900 degrees. A regular heptagon: An irregular heptagon:

Octagon An eight-sided polygon. The sum of the angles of an octagon is 1080 degrees. A regular octagon: An irregular octagon:

Nonagon A nine-sided polygon. The sum of the angles of a nonagon is 1260 degrees. A regular nonagon: An irregular nonagon:

Decagon A ten-sided polygon. The sum of the angles of a decagon is 1440 degrees. A regular decagon: An irregular decagon:

Diagonals of a Regular Polygon How many diagonals can be drawn from one vertex of a regular pentagon? How many triangles do the diagonals form?

Diagonals of a Regular Polygon You can also multiply the number of triangles inside a polygon by 180 o to find the sum of the interior angles. 3 • 180 o 540 o

Diagonals of a Regular Polygon How many diagonals can be drawn from one vertex of a regular pentagon? How many triangles do the diagonals form?

Diagonals of a Regular Polygon How many diagonals can be drawn from one vertex of a regular pentagon? How many triangles do the diagonals form? 6 • 180 o 1080 o

Interior Angles of Polygons In an n-sided polygon in which the measure of each interior angle is less than 180 o, the sum of the measures of the interior angles is (n – 2) • 180 o (n – 2) • (6 – 2) • 180 o (4) • 180 o 720 o

Interior Angles of Polygons (n – 2) • 180 o o (8 – 2) • 180 (6) • 180 o 1080 o

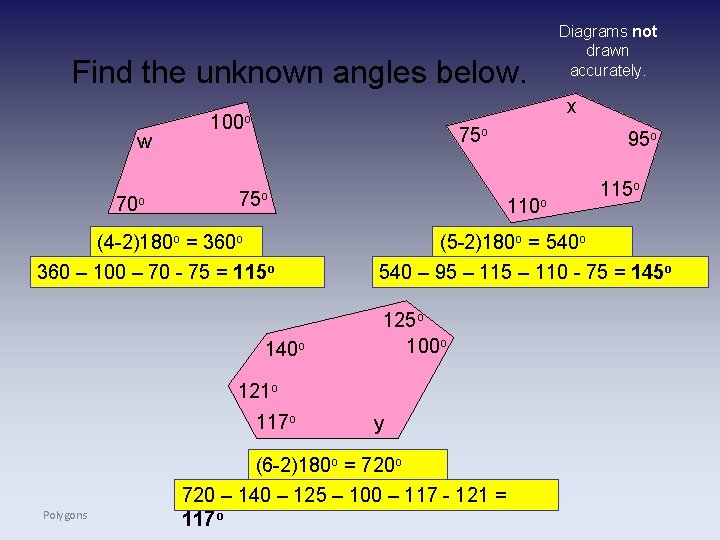
Find the unknown angles below. w 70 o x 100 o 75 o (4 -2)180 o = 360 o 360 – 100 – 70 - 75 = 115 o 140 o 117 o 95 o 110 o 115 o (5 -2)180 o = 540 o 540 – 95 – 110 - 75 = 145 o 125 o 100 o 121 o Polygons Diagrams not drawn accurately. y (6 -2)180 o = 720 o 720 – 140 – 125 – 100 – 117 - 121 = 117 o

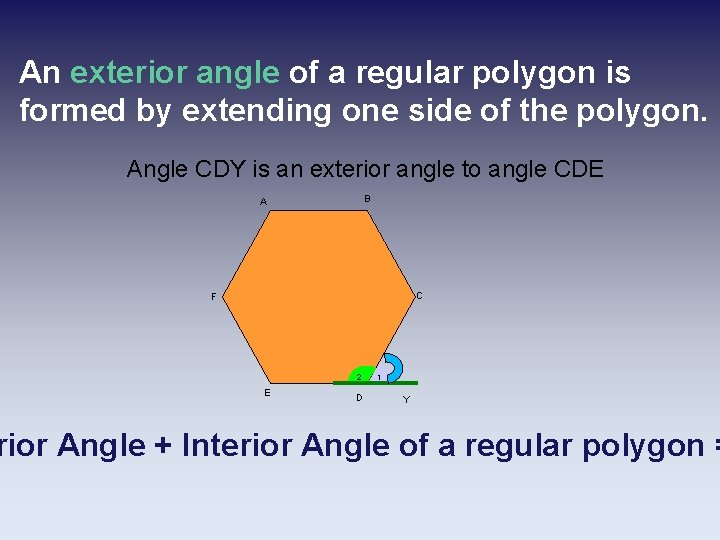
An exterior angle of a regular polygon is formed by extending one side of the polygon. Angle CDY is an exterior angle to angle CDE B A C F 2 E D 1 Y rior Angle + Interior Angle of a regular polygon =

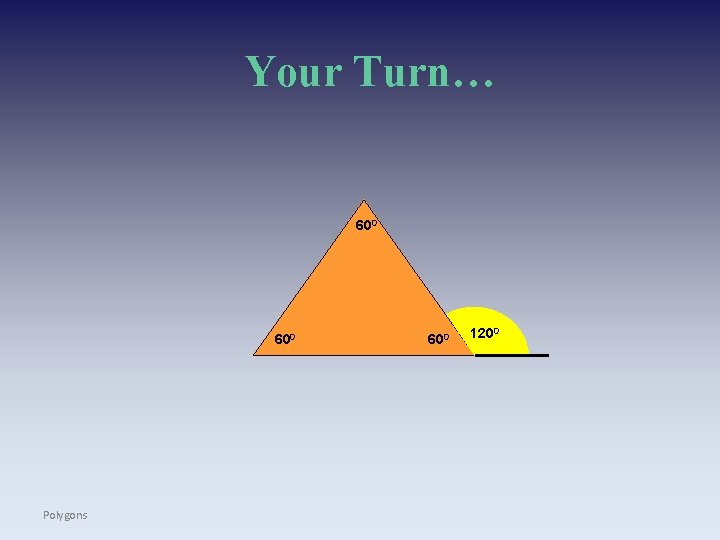
Your Turn… 600 Polygons 600 1200

Polygons 9. 6 Notes v closed figure made by three or more segments called sides. Measure of Interior Angles • Decompose polygons into triangles Number of triangles • 180 o OR (number of sides – 2) • 180 o Measure of Exterior Angles • Extend one side of polygon Exterior angle + Interior angle = 180 o