Polygone und Polyeder Regulre Polygone Oktagon Quadrat Hexagon

Polygone und Polyeder

Reguläre Polygone Oktagon Quadrat Hexagon Dreieck Pentagon

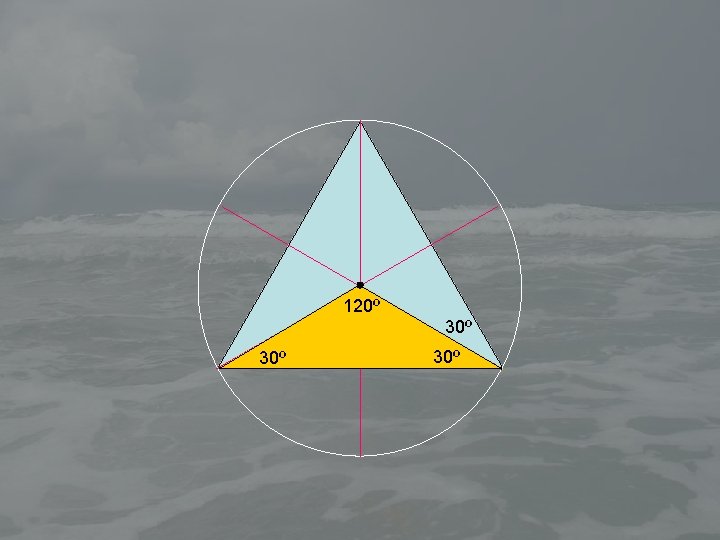
120º 30º 30º

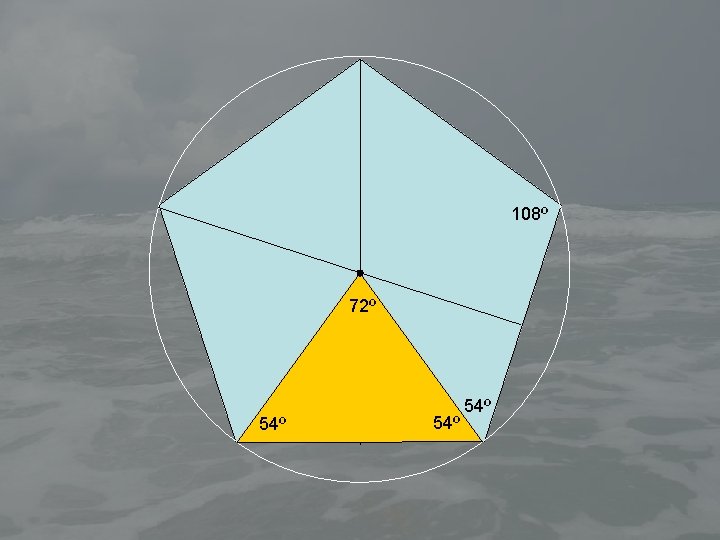
108º 72º 54º 54º

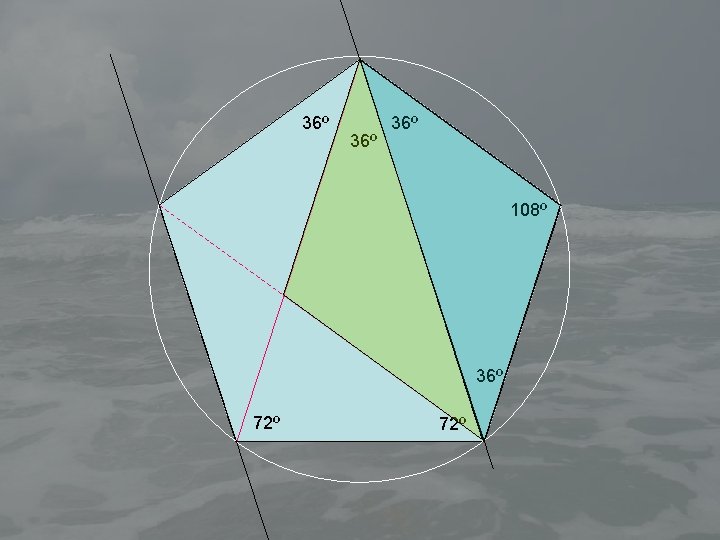
36º 36º 108º 36º 72º

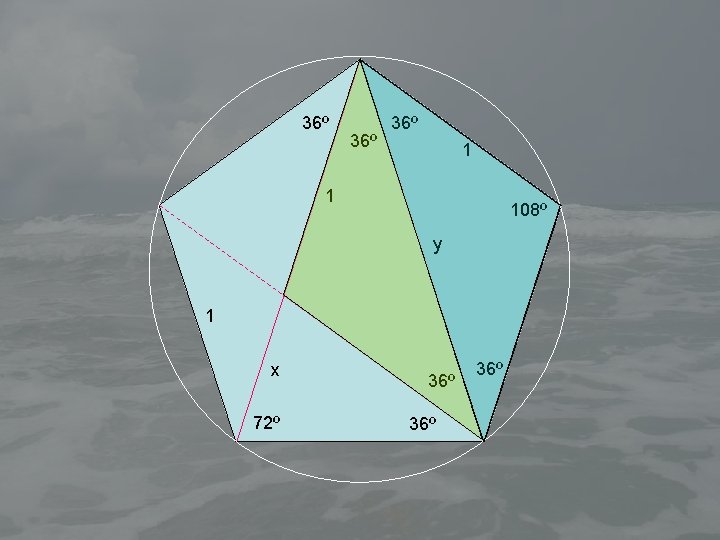
36º 36º 1 1 108º y 1 x 72º 36º 36º

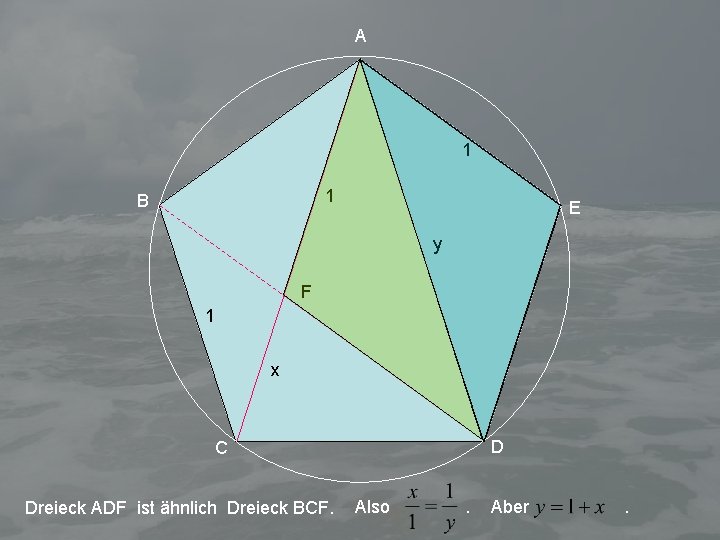
A 1 1 B E y F 1 x D C Dreieck ADF ist ähnlich Dreieck BCF. Also . Aber .

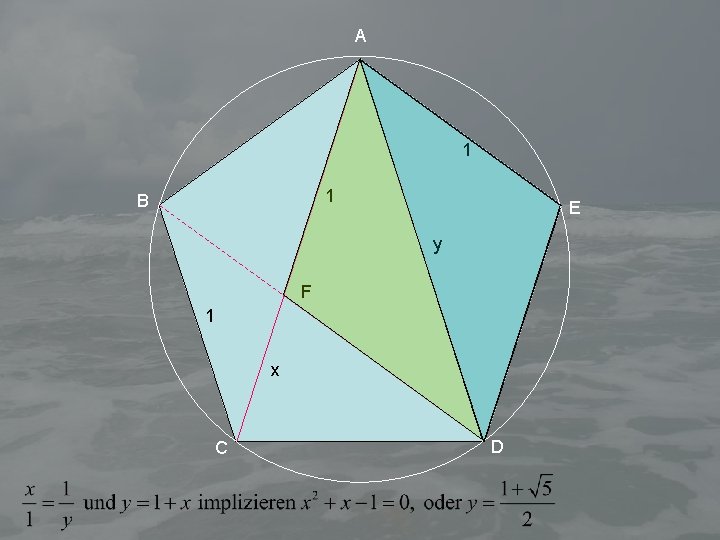
A 1 1 B E y F 1 x C D

Der Goldene Schnitt 1 x 1 -x

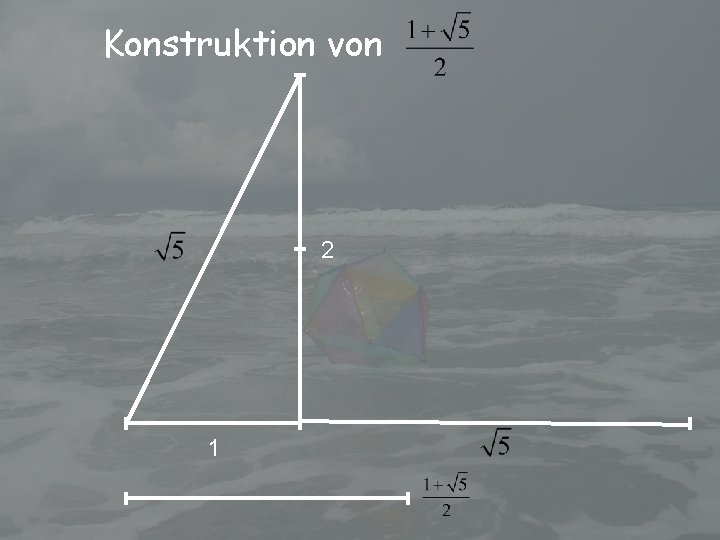
Konstruktion von 2 1

Pentagon: 1) Konstruiere das Goldene Dreieck 2) Konstruiere das Pentagon

Welche regulären Polygone können mit Zirkel und Lineal konstruiert werden? The reguläre Septagon (Heptagon) kann nicht mit Zirkel un Lineal konstruiert werden!

Platonische Körper Reguläre Polyeder, welche konvex sind und kongruente reguläre Polygone als Seitenflächen haben, und an jedem Eckpunkt treffen gleich viele Flächen zusammen. Es gibt genau fünf: Tetraeder, Cubus = Hexaeder, Oktaeder, Ikosaeder und Dodekaeder 20 12

Beispiel Oktaeder konvex Boot nicht konvex

“of a Fractal Nature” Photography by Gayla Chandler http: //www. public. asu. edu/~starlite/

Warum fünf Platonische Körper? Schritt 1: Peripheriewinkel der Seitenflächen Jede Seitenfläche ist ein reguläres Polygon Partition des Polygons in n Dreiecke Summe aller Winkel: Summe aller Winkel im Zentrum: Summe der Peripheriewinkel: Ein Peripheriewinkel:

Warum fünf Platonische Körper? Peripheriewinkel: Dreieck: Quadrat: Pentagon: Hexagon: Septagon:

Warum fünf Platonische Körper? Schritt 2: An einem Eckpunkt muss die Summe der Peripheriewinkel kleiner als sein:

Warum fünf Platonische Körper? Schritt 3: In einem Eckpunkt treffen mindestens 3 Seitenflächen zusammen. Also müssen die Peripheriewinkel kleiner als sein: . Dreiecke:

Warum fünf Platonische Körper? Schritt 3: In einem Eckpunkt treffen mindestens 3 Seitenflächen zusammen. Also müssen die Peripheriewinkel kleiner als sein: . Quadrat:

Warum fünf Platonische Körper? Schritt 3: In einem Eckpunkt treffen mindestens 3 Seitenflächen zusammen. Also müssen die Peripheriewinkel kleiner als sein: . Pentagon:

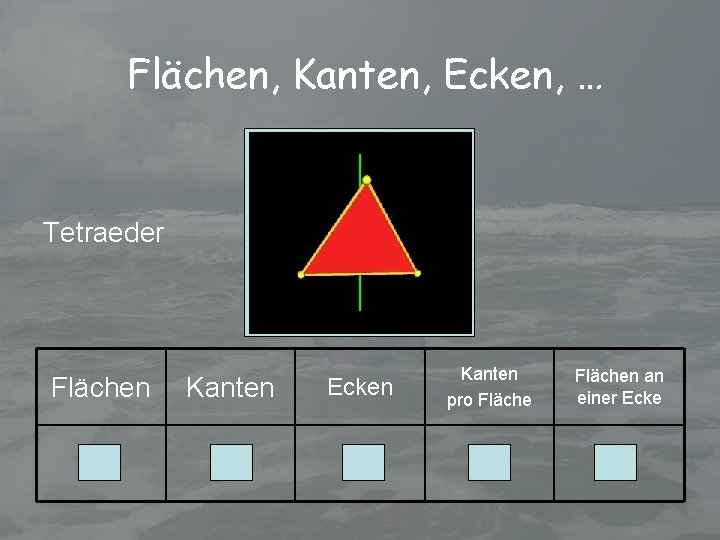
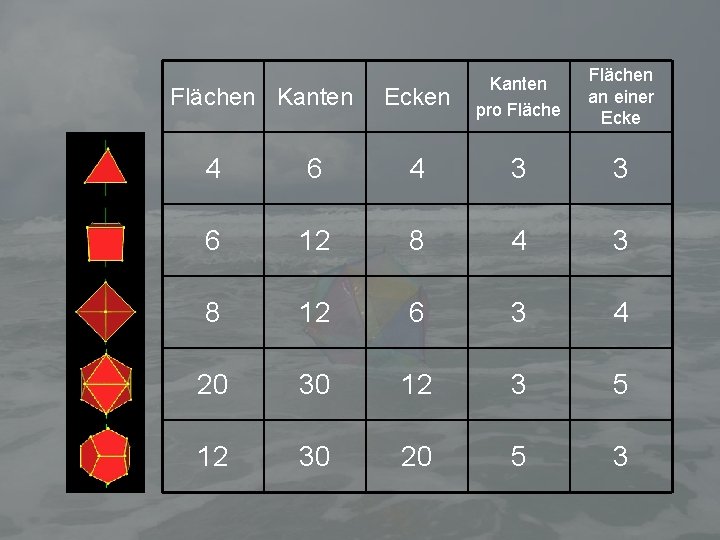
Flächen, Kanten, Ecken, … Tetraeder Flächen Kanten Ecken 4 6 4 Kanten pro Flächen an einer Ecke 3 3

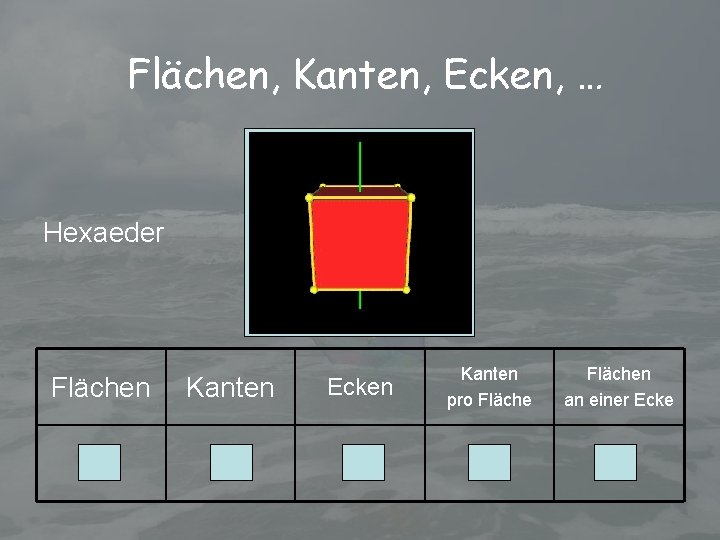
Flächen, Kanten, Ecken, … Hexaeder Flächen Kanten Ecken 6 12 8 Kanten pro Flächen an einer Ecke 4 3

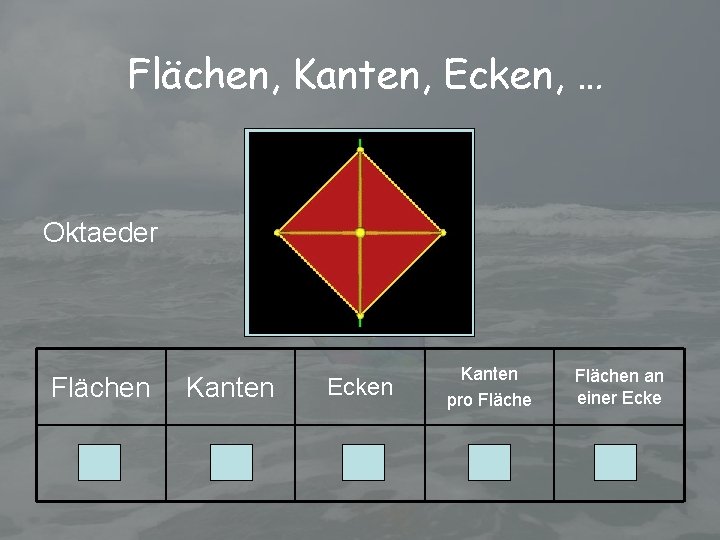
Flächen, Kanten, Ecken, … Oktaeder Flächen Kanten Ecken 8 12 6 Kanten pro Flächen an einer Ecke 3 4

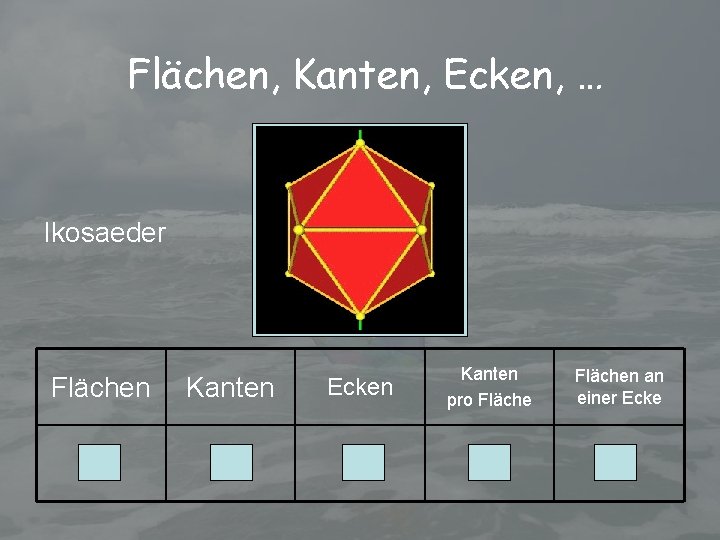
Flächen, Kanten, Ecken, … Ikosaeder Flächen Kanten Ecken 20 30 12 Kanten pro Flächen an einer Ecke 3 5

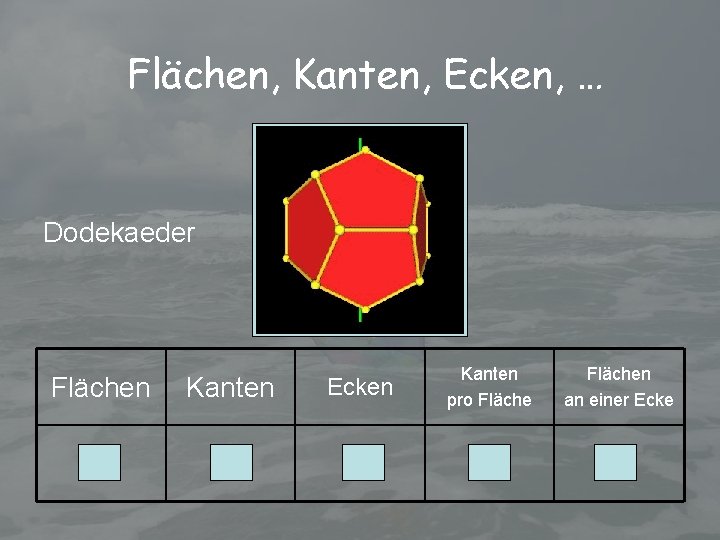
Flächen, Kanten, Ecken, … Dodekaeder Flächen Kanten Ecken 12 30 20 Kanten pro Flächen an einer Ecke 5 3

Flächen Kanten Ecken Kanten pro Flächen an einer Ecke 4 6 4 3 3 6 12 8 4 3 8 12 6 3 4 20 30 12 3 5 12 30 20 5 3

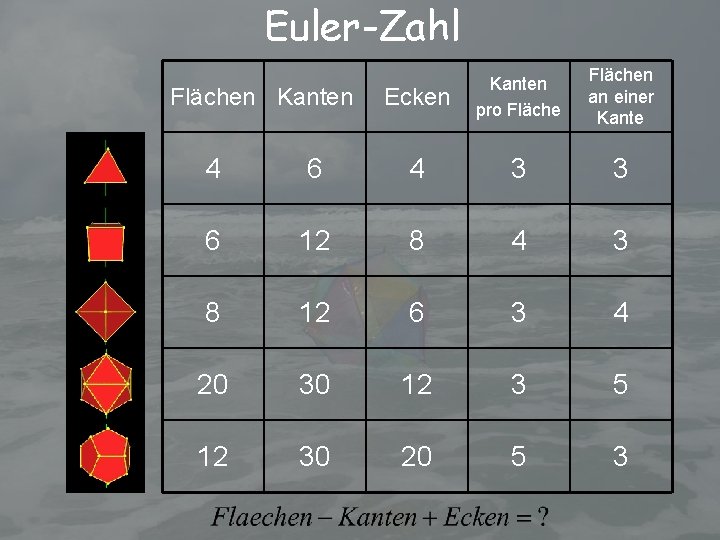
Euler-Zahl Flächen Kanten Ecken Kanten pro Flächen an einer Kante 4 6 4 3 3 6 12 8 4 3 8 12 6 3 4 20 30 12 3 5 12 30 20 5 3

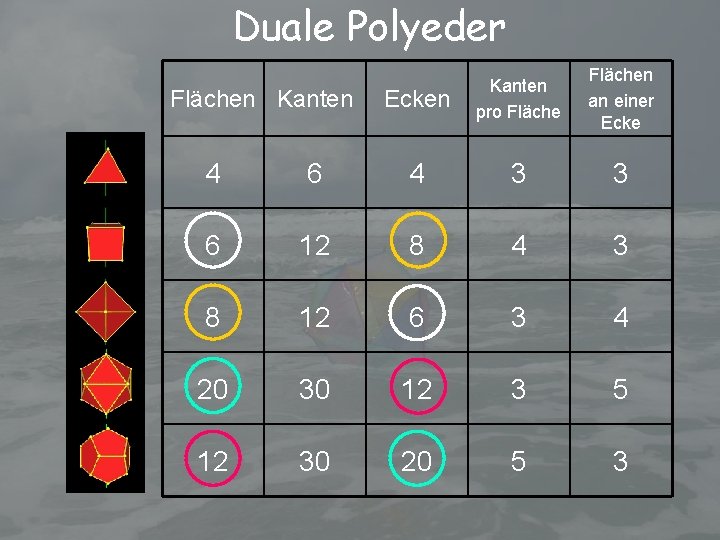
Duale Polyeder Flächen Kanten Ecken Kanten pro Flächen an einer Ecke 4 6 4 3 3 6 12 8 4 3 8 12 6 3 4 20 30 12 3 5 12 30 20 5 3

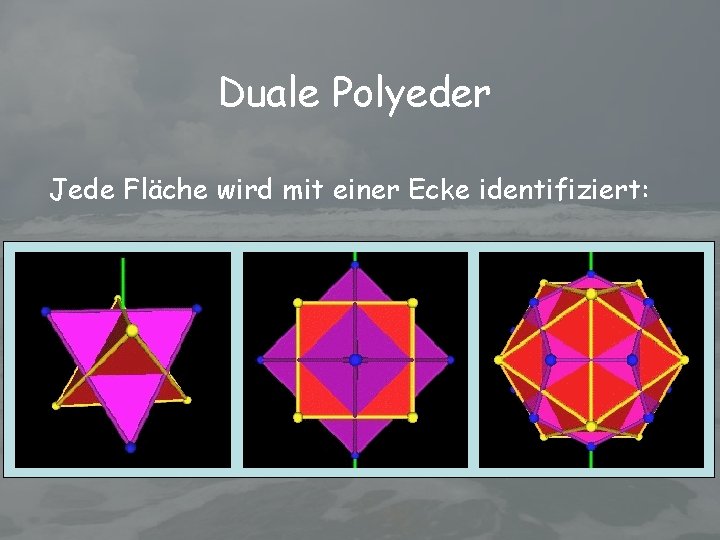
Duale Polyeder Jede Fläche wird mit einer Ecke identifiziert:

Duale Polyeder Jede Fläche wird mit einer Ecke identifiziert:

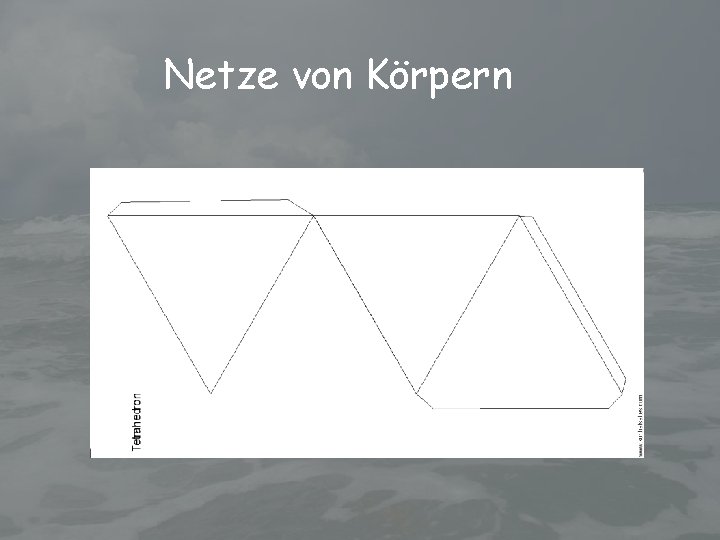
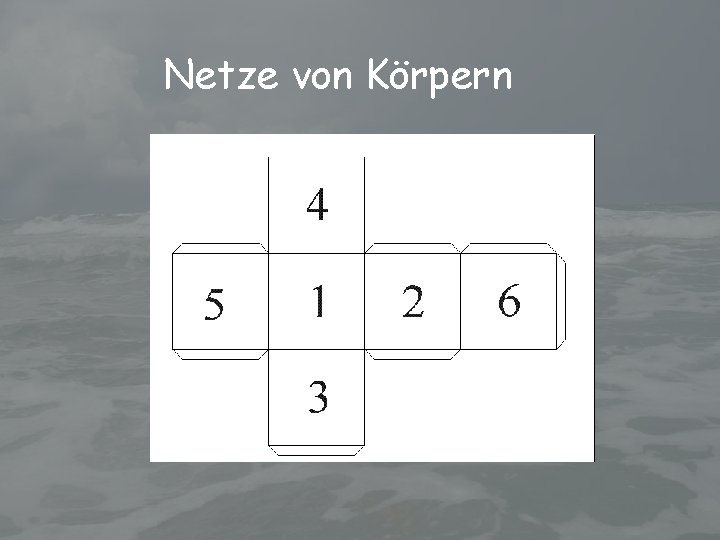
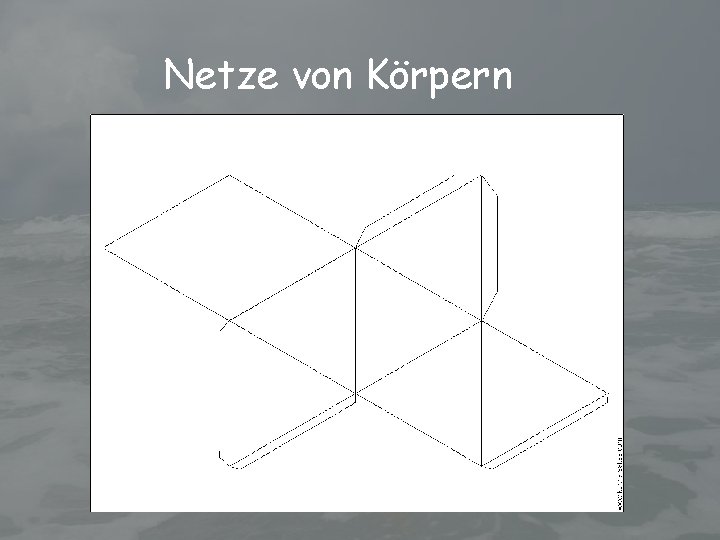
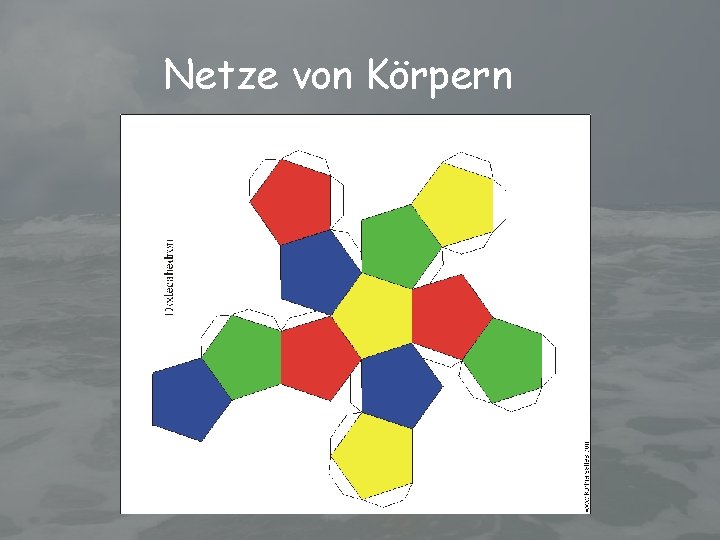
Netze von Körpern

Netze von Körpern

Netze von Körpern

Netze von Körpern

Netze von Körpern

Netze von Körpern

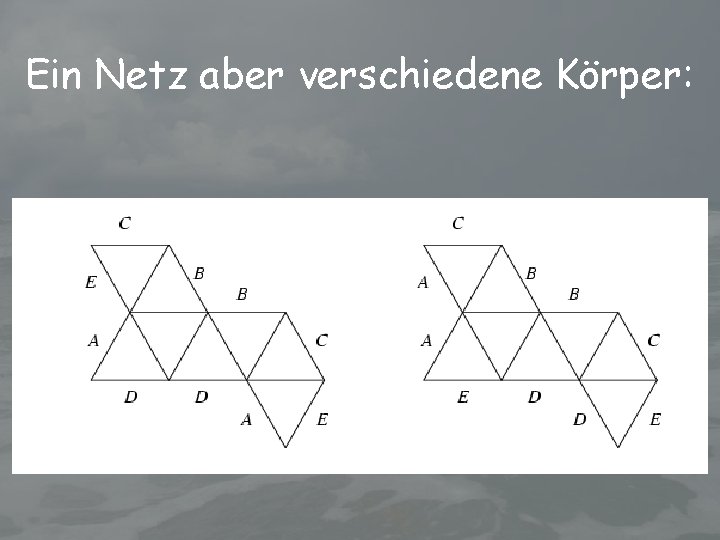
Ein Netz aber verschiedene Körper:

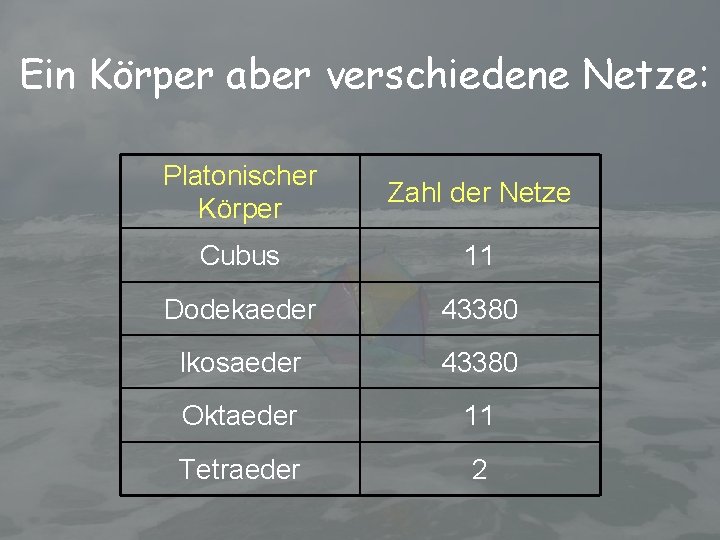
Ein Körper aber verschiedene Netze:

Ein Körper aber verschiedene Netze: Platonischer Körper Zahl der Netze Cubus 11 Dodekaeder 43380 Ikosaeder 43380 Oktaeder 11 Tetraeder 2

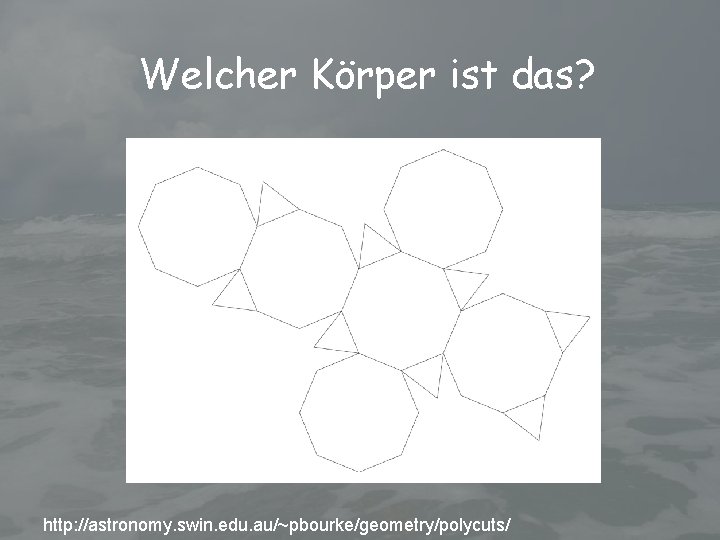
Welcher Körper ist das? http: //astronomy. swin. edu. au/~pbourke/geometry/polycuts/

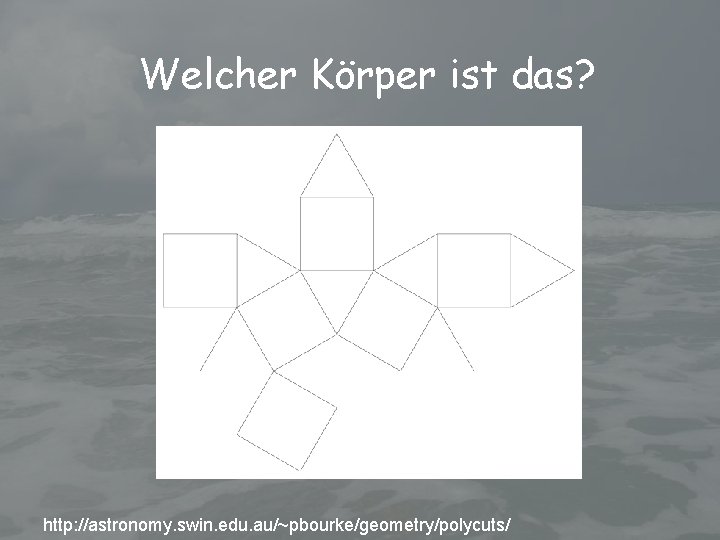
Welcher Körper ist das? http: //astronomy. swin. edu. au/~pbourke/geometry/polycuts/

Welcher Körper ist das? http: //astronomy. swin. edu. au/~pbourke/geometry/polycuts/