Polygon Scan Conversion Instructor Paul Merrell Rasterization Rasterization

Polygon Scan Conversion Instructor: Paul Merrell

Rasterization • Rasterization takes shapes like triangles and determines which pixels to fill. 2

Filling Polygons First approach: 1. Polygon Scan-Conversion • Rasterize a polygon scan line by scan line, determining which pixels to fill on each line. 3

Filling Polygons Second Approach: 2. Polygon Fill • Select a pixel inside the polygon. Grow outward until the whole polygon is filled. 4

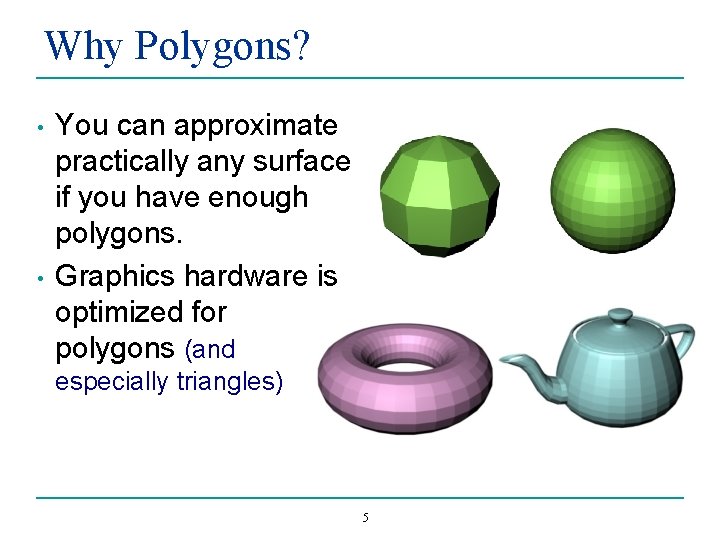
Why Polygons? • • You can approximate practically any surface if you have enough polygons. Graphics hardware is optimized for polygons (and especially triangles) 5

Coherence Scan-line Edge Span 6

Polygon Scan Conversion Intersection Points Other points in the span 7

Polygon Scan Conversion Process each scan line • 1. 2. 3. Find the intersections of the scan line with all polygon edges. Sort the intersections by x coordinate. Fill in pixels between pairs of intersections using an odd-parity rule. - - Set parity even initially. Each intersection flips the parity. Draw when parity is odd. 8

Polygon Scan-Conversion • Process for scan converting polygons • • • Process one polygon at a time. Store information about every polygon edge. Compute spans for each scan line. Draw the pixels between the spans. This can be optimized using an table that stores information about each edge. Perform scan conversion one scan line at a time. 9

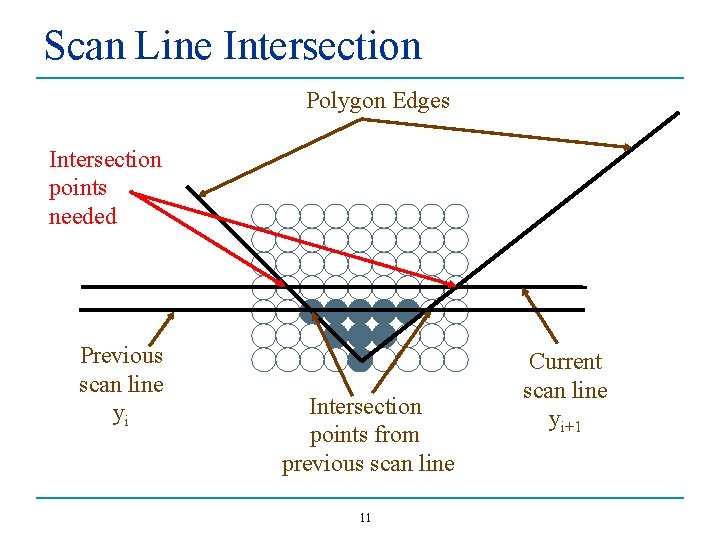
Computing Intersections • • • For each scan line, we need to know if it intersects the polygon edges. It is expensive to compute a complete line-line intersection computation for each scan line. After computing the intersection between a scan line and an edge, we can use that information in the next scan line. 10

Scan Line Intersection Polygon Edges Intersection points needed Previous scan line yi Intersection points from previous scan line 11 Current scan line yi+1

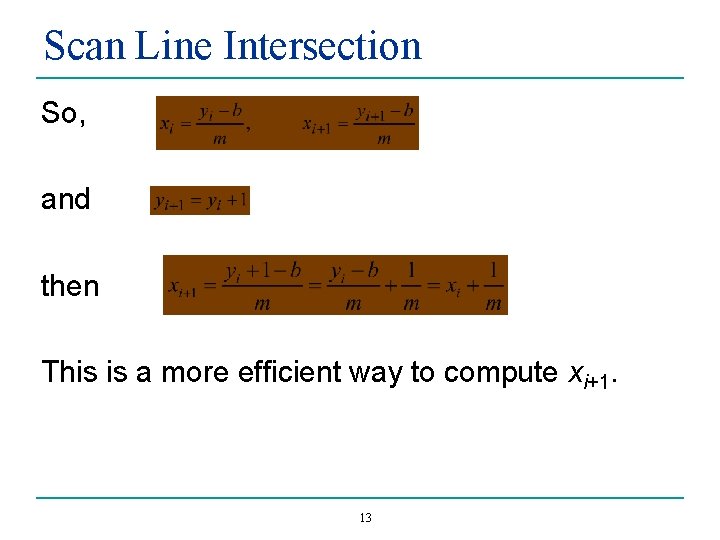
Scan Line Intersection Use edge coherence to incrementally update the x intersections. (x , y We know @ymax (x@ymin, ymin) Each new scan line is 1 greater in y We need to compute x for a given scan line, 12 max)

Scan Line Intersection So, and then This is a more efficient way to compute xi+1. 13

Edge Tables • We will use two different edge tables: • Active Edge Table (AET) • • Stores all edges that intersect the current scan line. Global Edge Table (GET) • • Stores all polygon edges. Used to update the AET. 14

Active Edge Table • • Table contains one entry per edge intersected by the current scan line. At each new scan line: • • Compute new intersections for all edges using the formula. Add any new edges intersected. Remove any edges no longer intersected. To efficiently update the AET, we will can use a global edge table (GET) 15

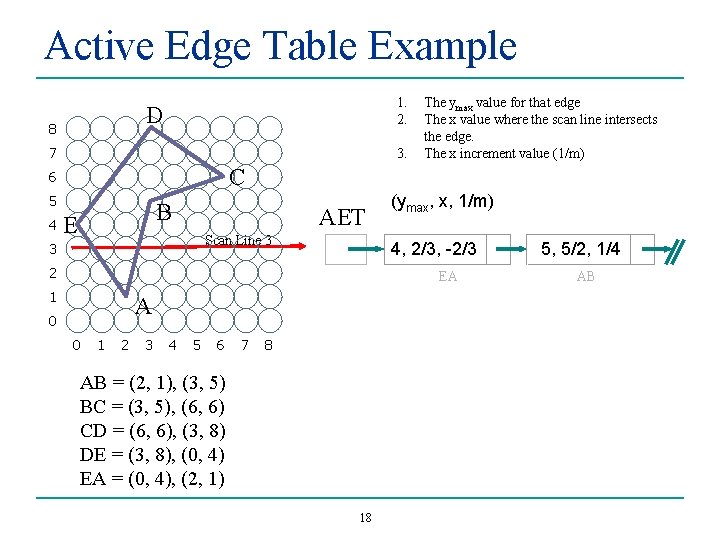
Global Edge Table Example D 8 GET 7 5 4 8 C 6 3 6 2 Indexed by 5 scan line 4 1 A 0 0 1 2 3 4 (ymax, x@ymin, 1/m) 7 B E Place entries into the GET based on the ymin values. 5 6 AB = (2, 1), (3, 5) BC = (3, 5), (6, 6) CD = (6, 6), (3, 8) DE = (3, 8), (0, 4) EA = (0, 4), (2, 1) 7 8 CD BC DE 8, 6, -3/2 6, 3, 3 8, 0, ¾ 3 2 1 0 16 AB 5, 2, ¼ EA 4, 2, -2/3

Active Edge Table Example • • The active edge table stores information about the edges that intersect the current scan line. Entries are • • The ymax value of the edge The x value where the edge intersects the current scan line. The x increment value (1/m) Entries are sorted by x values. 17

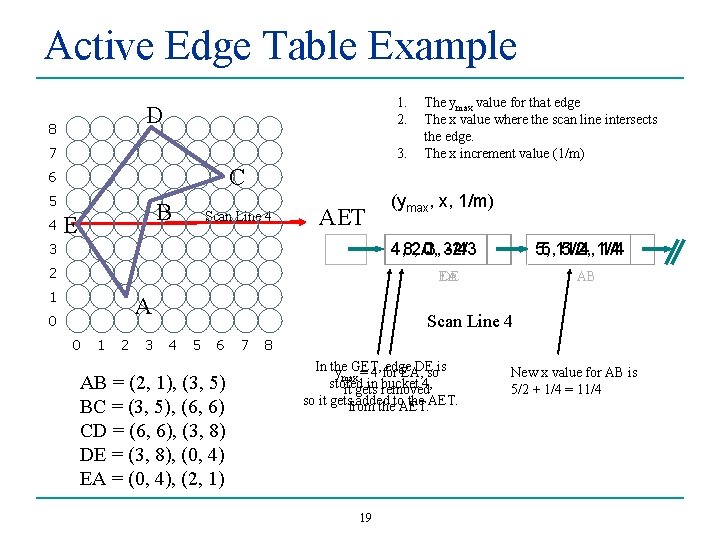
Active Edge Table Example 1. 2. D 8 7 3. C 6 5 4 The ymax value for that edge The x value where the scan line intersects the edge. The x increment value (1/m) B E AET Scan Line 3 3 (ymax, x, 1/m) 4, 2/3, -2/3 2 EA 1 A 0 0 1 2 3 4 5 6 7 8 AB = (2, 1), (3, 5) BC = (3, 5), (6, 6) CD = (6, 6), (3, 8) DE = (3, 8), (0, 4) EA = (0, 4), (2, 1) 18 5, 5/2, 1/4 AB

Active Edge Table Example 1. 2. D 8 7 3. C 6 5 4 The ymax value for that edge The x value where the scan line intersects the edge. The x increment value (1/m) B E Scan Line 4 AET (ymax, x, 1/m) 4, 8, 2/3, 0, 3/4 -2/3 3 2 5, 5, 11/4, 5/2, 1/4 EA DE 1 A 0 0 1 2 3 AB Scan Line 4 4 5 6 AB = (2, 1), (3, 5) BC = (3, 5), (6, 6) CD = (6, 6), (3, 8) DE = (3, 8), (0, 4) EA = (0, 4), (2, 1) 7 8 In the edge DEsois ymax. GET, = 4 for EA, stored in removed bucket 4, it gets so it getsfrom added the AET. theto. AET. 19 New x value for AB is 5/2 + 1/4 = 11/4

Active Edge Table Example 1. 2. D 8 7 3. C 6 5 4 The ymax value for that edge The x value where the scan line intersects the edge. The x increment value (1/m) Scan Line 5 B E AET (ymax, x, 1/m) 8, 8, 3/4, 0, 3/4 3 2 DE 1 A 0 0 1 2 3 Increment x = 0 + 3/4 4 5 6 7 8 AB = (2, 1), (3, 5) BC = (3, 5), (6, 6) CD = (6, 6), (3, 8) DE = (3, 8), (0, 4) EA = (0, 4), (2, 1) 20 5, 11/4, 6, 3, 3 1/4 AB BC Remove AB, Add BC since it is since ymax in=the 5. GET at ymin = 5.

Active Edge Table Example D 8 7 C 6 5 4 Scan Line 6 B E 3 2 1 A 0 0 1 2 3 4 5 6 7 8 AB = (2, 1), (3, 5) BC = (3, 5), (6, 6) CD = (6, 6), (3, 8) DE = (3, 8), (0, 4) EA = (0, 4), (2, 1) 21

Clipping

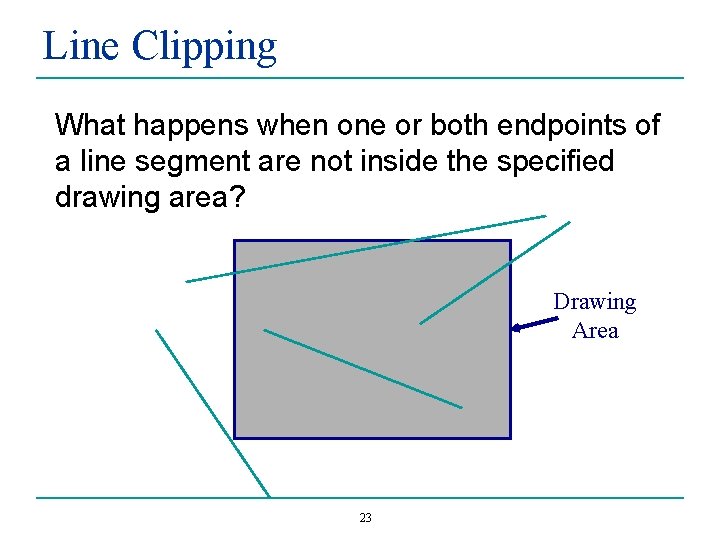
Line Clipping What happens when one or both endpoints of a line segment are not inside the specified drawing area? Drawing Area 23

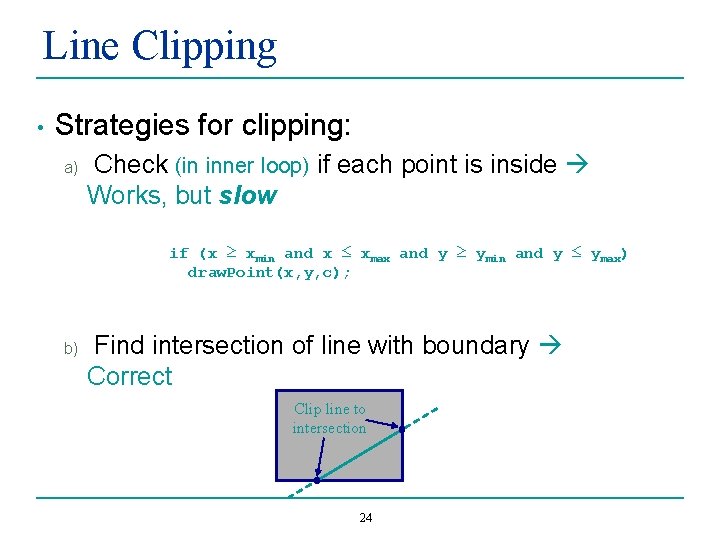
Line Clipping • Strategies for clipping: a) Check (in inner loop) if each point is inside Works, but slow if (x ≥ xmin and x ≤ xmax and y ≥ ymin and y ≤ ymax) draw. Point(x, y, c); b) Find intersection of line with boundary Correct Clip line to intersection 24

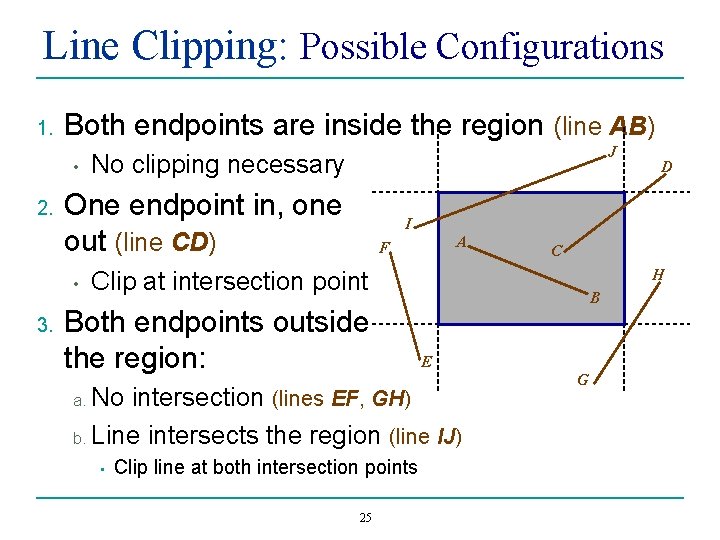
Line Clipping: Possible Configurations 1. Both endpoints are inside the region (line AB) • 2. No clipping necessary One endpoint in, one out (line CD) • 3. J I A F C H Clip at intersection point Both endpoints outside the region: B E No intersection (lines EF, GH) b. Line intersects the region (line IJ) a. • D Clip line at both intersection points 25 G

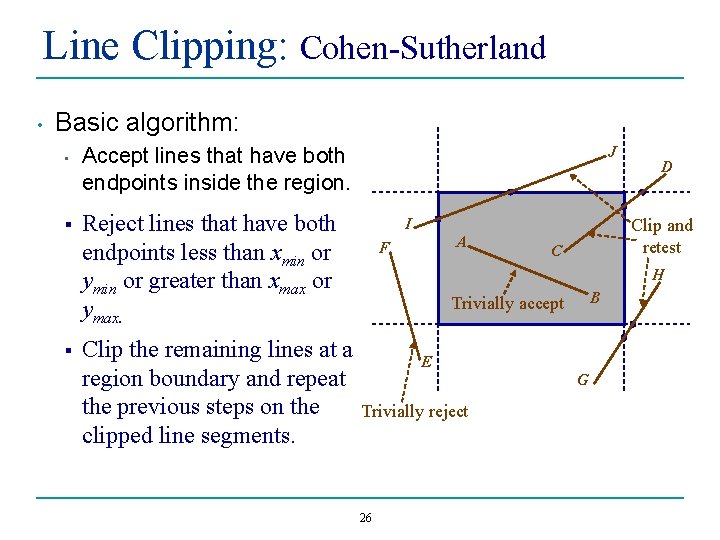
Line Clipping: Cohen-Sutherland • Basic algorithm: • § § J Accept lines that have both endpoints inside the region. Reject lines that have both endpoints less than xmin or ymin or greater than xmax or ymax. Clip the remaining lines at a region boundary and repeat the previous steps on the clipped line segments. I A F D Clip and retest C H B Trivially accept E G Trivially reject 26

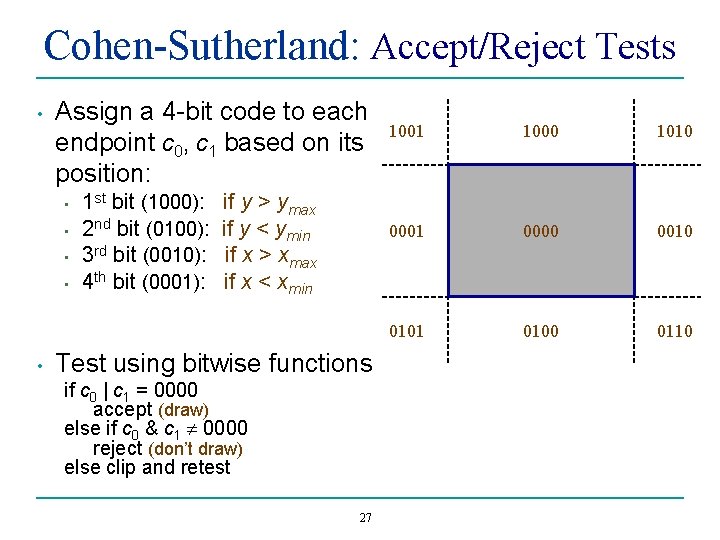
Cohen-Sutherland: Accept/Reject Tests • Assign a 4 -bit code to each endpoint c 0, c 1 based on its position: • • • 1 st bit (1000): 2 nd bit (0100): 3 rd bit (0010): 4 th bit (0001): if y > ymax if y < ymin if x > xmax if x < xmin Test using bitwise functions if c 0 | c 1 = 0000 accept (draw) else if c 0 & c 1 0000 reject (don’t draw) else clip and retest 27 1001 1000 1010 0001 0000 0010 0101 0100 0110

Cohen-Sutherland Accept/Reject • Accept/reject/redo all based on bit-wise Boolean ops. 1001 1000 1010 0001 0000 0010 0101 0100 0110 28

Polygon Clipping What about polygons? 29

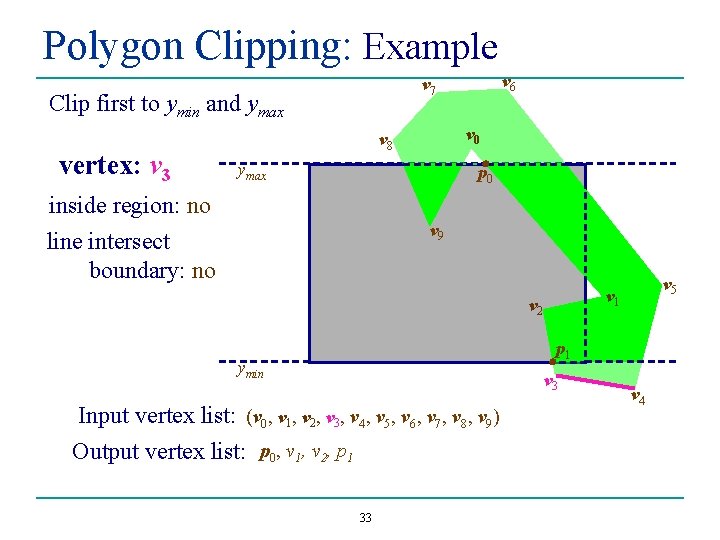
Polygon Clipping: Example Clip first to ymin and ymax vertex: v 0 v 6 v 7 v 0 v 8 ymax p 0 Inside region: No Line intersect boundary: Yes v 9 v 2 Add p 0 to output list ymin v 3 Input vertex list: (v 0, v 1, v 2, v 3, v 4, v 5, v 6, v 7, v 8, v 9) Output vertex list: p 0 30 v 5 v 1 v 4

Polygon Clipping: Example Clip first to ymin and ymax vertex: v 1 v 6 v 7 v 0 v 8 ymax p 0 inside region: yes line intersect boundary: no v 9 v 2 add v 1 to output list ymin v 3 Input vertex list: (v 0, v 1, v 2, v 3, v 4, v 5, v 6, v 7, v 8, v 9) Output vertex list: p 0 , v 1 31 v 5 v 1 v 4

Polygon Clipping: Example Clip first to ymin and ymax vertex: v 2 v 6 v 7 v 0 v 8 ymax p 0 inside region: yes line intersect boundary: yes v 9 v 2 add v 2, p 1 to output list v 5 v 1 p 1 ymin v 3 Input vertex list: (v 0, v 1, v 2, v 3, v 4, v 5, v 6, v 7, v 8, v 9) Output vertex list: p 0 , v 1 , v 2, p 1 32 v 4

Polygon Clipping: Example Clip first to ymin and ymax vertex: v 3 v 6 v 7 v 0 v 8 ymax p 0 inside region: no line intersect boundary: no v 9 v 5 v 1 v 2 p 1 ymin v 3 Input vertex list: (v 0, v 1, v 2, v 3, v 4, v 5, v 6, v 7, v 8, v 9) Output vertex list: p 0, v 1, v 2, p 1 33 v 4

Polygon Clipping: Example Clip first to ymin and ymax vertex: v 4 v 6 v 7 v 0 v 8 ymax p 0 inside region: no line intersect boundary: yes v 9 v 2 add p 2 to output list v 5 v 1 p 1 ymin v 3 Input vertex list: (v 0, v 1, v 2, v 3, v 4, v 5, v 6, v 7, v 8, v 9) Output vertex list: p 0, v 1, v 2, p 1 , p 2 34 p 2 v 4

Polygon Clipping: Example Clip first to ymin and ymax vertex: v 5 v 6 v 7 v 0 v 8 ymax p 3 p 0 inside region: yes line intersect boundary: yes v 9 v 2 add v 5, p 3 to output list v 5 v 1 p 1 ymin v 3 Input vertex list: (v 0, v 1, v 2, v 3, v 4, v 5, v 6, v 7, v 8, v 9) Output vertex list: p 0, v 1, v 2, p 1, p 2 , v 5, p 3 35 p 2 v 4

Polygon Clipping: Example Clip first to ymin and ymax vertex: v 6 v 7 v 0 v 8 ymax p 3 p 0 inside region: no line intersect boundary: no v 9 v 5 v 1 v 2 p 1 ymin v 3 Input vertex list: (v 0, v 1, v 2, v 3, v 4, v 5, v 6, v 7, v 8, v 9) Output vertex list: p 0, v 1, v 2, p 1, p 2, v 5, p 3 36 p 2 v 4

Polygon Clipping: Example Clip first to ymin and ymax vertex: v 7 v 6 v 7 v 0 v 8 ymax p 3 p 0 inside region: no line intersect boundary: no v 9 v 5 v 1 v 2 p 1 ymin v 3 Input vertex list: (v 0, v 1, v 2, v 3, v 4, v 5, v 6, v 7, v 8, v 9) Output vertex list: p 0, v 1, v 2, p 1, p 2, v 5, p 3 37 p 2 v 4

Polygon Clipping: Example Clip first to ymin and ymax vertex: v 8 v 6 v 7 v 8 ymax v 0 p 4 p 3 p 0 inside region: no line intersect boundary: yes v 9 v 2 add p 4 to output list v 5 v 1 p 1 ymin v 3 Input vertex list: (v 0, v 1, v 2, v 3, v 4, v 5, v 6, v 7, v 8, v 9) Output vertex list: p 0, v 1, v 2, p 1, p 2, v 5, p 3, p 4 38 p 2 v 4

Polygon Clipping: Example Clip first to ymin and ymax vertex: v 9 v 6 v 7 v 8 ymax inside region: yes line intersect boundary: yes p 4 p 5 v 0 p 3 p 0 v 9 v 2 add v 9, p 5 to output list v 5 v 1 p 1 ymin v 3 Input vertex list: (v 0, v 1, v 2, v 3, v 4, v 5, v 6, v 7, v 8, v 9) Output vertex list: p 0, v 1, v 2, p 1, p 2, v 5, p 3, p 4 , v 9, p 5 39 p 2 v 4

Polygon Clipping: Example This gives us a new polygon p 4 ymax p 5 p 3 p 0 v 9 v 2 p 1 ymin with vertices: (p 0, v 1, v 2, p 1, p 2, v 5, p 3, p 4, v 9, p 5) 40 v 5 v 1 p 2

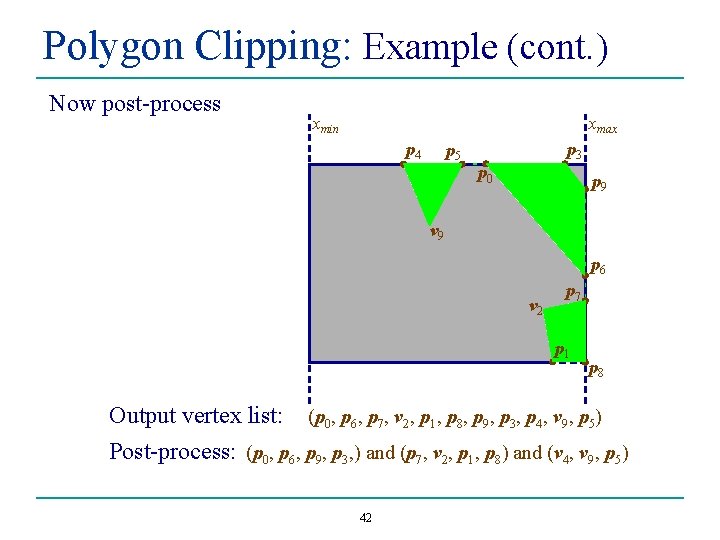
Polygon Clipping: Example (cont. ) Now clip to xmin and xmax xmin xmax p 4 p 5 p 3 p 0 p 9 v 9 p 6 v 2 p 7 p 1 Input vertex list: = (p 0, v 1, v 2, p 1, p 2, v 5, p 3, p 4, v 9, p 5) Output vertex list: (p 0, p 6, p 7, v 2, p 1, p 8, p 9, p 3, p 4, v 9, p 5) 41 v 5 v 1 p 8 p 2

Polygon Clipping: Example (cont. ) Now post-process xmin xmax p 4 p 5 p 3 p 0 p 9 v 9 p 6 v 2 p 7 pv 13 Output vertex list: p 8 (p 0, p 6, p 7, v 2, p 1, p 8, p 9, p 3, p 4, v 9, p 5) Post-process: (p 0, p 6, p 9, p 3, ) and (p 7, v 2, p 1, p 8) and (v 4, v 9, p 5) 42

Transformations

General Transformations • Want to be able to manipulate graphical objects: • • • Translation: move an object Rotation: change orientation Scale: change size Other transformations: reflection, shear, etc. A general 2 -D transformation has the form: x´ = fx(x, y) y´ = fy(x, y) where x and y are the original coordinates and x´ and y´ are the transformed coordinates. • In vector form: 44

General Transformations (cont. ) • General transforms may be non-linear: • Lines do not necessarily map to lines • Every point (along lines, inside shapes, etc. ) needs to be transformed • Non-linear Transformations are harder to deal with. • Fortunately, many important transformations are linear. • Non-Linear Example: 7 y 7 6 6 5 5 4 4 3 3 2 2 1 0 0 x 1 2 3 4 5 6 7 45 y x 1 2 3 4 5 6 7

Linear Transformations • We will use linear transformations: x´ = fx(x, y) = axx + bxy + cx y´ = fy(x, y) = ayx + byy + cy • • Linear Transforms can be written using matrix operations: Advantages: • Lines transform to lines • Only need to transform vertices. • Computationally efficient • Problem: would like to simplify further get rid of T 46

Translation Move object from one place to another: • Forward transform: x´ = x + tx y´ = y + ty or p´ = p + T where 7 y 6 5 • Inverse transform: p = p´ – T 4 3 2 1 0 0 47 x 1 2 3 4 5 6 7

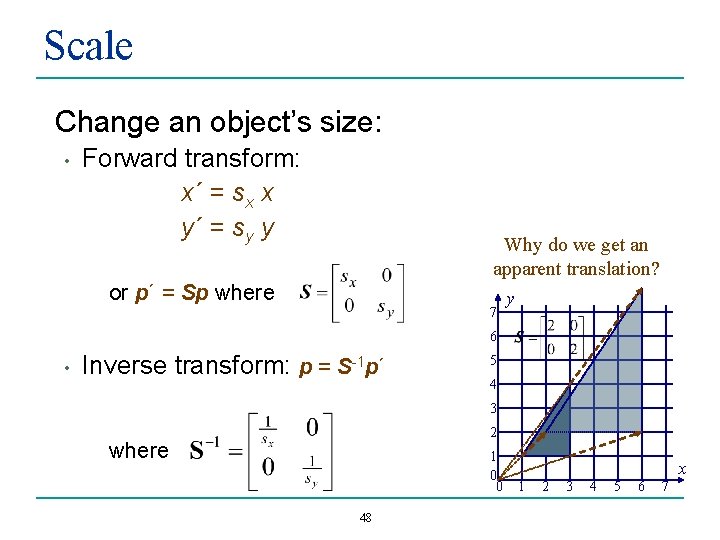
Scale Change an object’s size: • Forward transform: x´ = sx x y´ = sy y Why do we get an apparent translation? or p´ = Sp where 7 y 6 • Inverse transform: p = S-1 p´ 5 4 3 2 where 1 0 0 48 x 1 2 3 4 5 6 7

Scale • Properties of the scale: • • The scale is performed relative to the origin. A scale factor greater than one enlarges the objects and moves it away from the origin. A scale factor less than one shrinks the object and moves it towards the origin. Usually this isn’t what we want • Generally we would like to scale about the object’s center - not the coordinate origin. 49

Scale: Transforms Scale can accomplish the following transforms: • Uniform scale: sx = sy • • Non-uniform scale: sx sy • • Preserves angles, but not lengths 7 Doesn’t preserve angles or lengths 6 5 Reflection about the 4 x-axis: sx = 1, sy = – 1 y-axis: sx = – 1, sy = 1 line y = –x: sx = – 1, sy = – 1 • • • y 3 2 1 0 0 Reflection preserves angles and lengths What is the inverse matrix? A reflection matrix is its own inverse. x 1 2 3 4 y= 50 5 –x 6 7

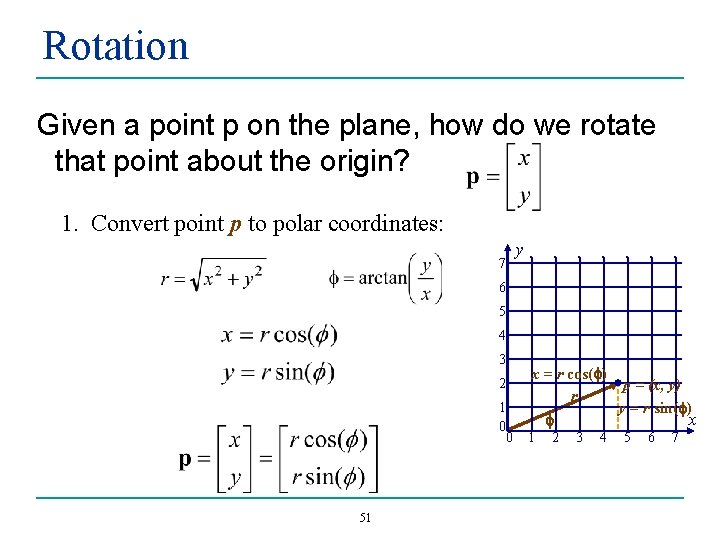
Rotation Given a point p on the plane, how do we rotate that point about the origin? 1. Convert point p to polar coordinates: 7 y 6 5 4 3 2 1 0 0 51 x = r cos(f) p = (x, y) r y = r sin(f) x f 1 2 3 4 5 6 7

Rotation (cont) Now, let’s rotate that point by q about the origin 7 2. To rotate q degrees, simply add q to f: y 6 5 p´= (x’, y’) 4 3 3. Apply the sum of angles formula 4. Substitute x and y back in: 52 2 1 0 0 r q 1 p = (x, y) r x f 2 3 4 5 6 7

Rotation (cont) So, given a point p that we wish to rotate about the origin, we simply multiply p by the rotation matrix 53

Rotating an Object Apply the rotation to each vertex of the object • Forward transform: x´ = x cos(q) – y sin(q) y´ = x sin(q) + y cos(q) or p´ = Rp where • Inverse rotation: p = 7 R-1 p´ y 6 5 4 3 q = 45° 2 1 q 0 0 1 54 x 2 3 4 5 6 7

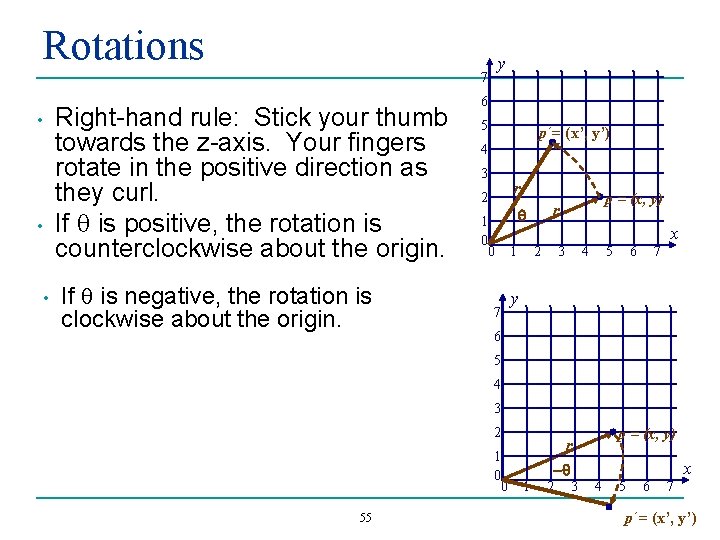
Rotations y 7 • • • Right-hand rule: Stick your thumb towards the z-axis. Your fingers rotate in the positive direction as they curl. If q is positive, the rotation is counterclockwise about the origin. If q is negative, the rotation is clockwise about the origin. 6 5 p´= (x’, y’) 4 3 r 2 1 0 0 7 q 1 p = (x, y) r x 2 3 4 5 6 7 y 6 5 4 3 2 1 0 0 55 p = (x, y) r 1 -q 2 x 3 4 5 6 7 p´= (x’, y’)

Composition • How can we do more complex transformations? • Scale an object in an arbitrary direction (other than in x and/or y) • • • Rotate an object about a point (other than the origin) Etc. Composition: combine basic transforms to achieve a more complex one • Example: Scale by ½ at a 30° angle • • Recall that a negative rotation matrix is the transpose of its corresponding positive rotation matrix. Rotate clockwise 30° (q = –p / 6): p´ = RTp Scale in x by ½: p´´ = Sp´ Rotate counter-clockwise 30° (q = p / 6): p´´´ = Rp´´ Final result: p´´´ = Rp´´ = RSp´ = RSRTp 56

Composition: Scale at Arbitrary Angle Scale object at an arbitrary angle q: 1. y 5 4 Rotate clockwise by q: p´ = 3 q = 30° RT p 2 1 0 0 x 1 2 3 4 5 y 4 2. Scale about origin: p´ = SRTp 3 2 5 3. Rotate back (counter-clockwise by q): p´ = RSRTp 4 3 q = 30° 2 1 0 0 57 1 0 0 y x 1 2 3 4

Composition and Efficiency • Multiple transformations: Multiply each point (i. e. , vertex) in an object by each basic transformation p´ = RSRTp • • • Requires multiple matrix multiplies per vertex Lots of extra computation if transforming thousands (or millions) of points. Composition: matrix multiply is associative • • Multiply matrices first to create a single matrix Multiply each point by a single matrix p´ = RSRTp = M p • Much more efficient 58

Rotation about an Arbitrary Point • • • Our rotations (so far) have been about the origin This rotation “moves” the entire object as it rotates Usually when we want to rotate an object, we want to rotate it about its center (or some other fixed point) How can we do this? Answer: Apply a sequence of transformations 59

Composition: Rotation About a Point Rotate object about an arbitrary point T: 1. y 5 4 3 Translate T to origin: p´ = p – 2 T 1 0 0 x 1 2 3 4 5 y 4 2. 3 Rotate about origin: p´ = R(p – 2 T) 5 1 0 0 y 4 3 3. Translate back: p´ = R(p – T) + T 60 2 1 0 0 x 1 2 3 4 q = 45° x 1 2 3 4

Rotation about an Arbitrary Point • Standard format for rotating about an arbitrary point: • • Translate point of rotation to the origin Rotate about the origin Translate the point back to its original position Compute the composite transformation that will accomplish this, then apply that transformation to all vertices in the object. 61

Homogeneous Coordinates • Problem: • • Rotation, scale, and shear multiply a matrix with p: p´ = Mp Translation adds a vector to p: p´ = p + T Would like to treat all transformations the same • Optimize the hardware • Compose transformations Solution: homogeneous coordinates • • Increase point’s dimensionality add a third coordinate w: Two homogeneous points (p 1 and p 2) specify the same 2 -D Cartesian point if: p 1 = cp 2 for some real-valued scalar number c 62

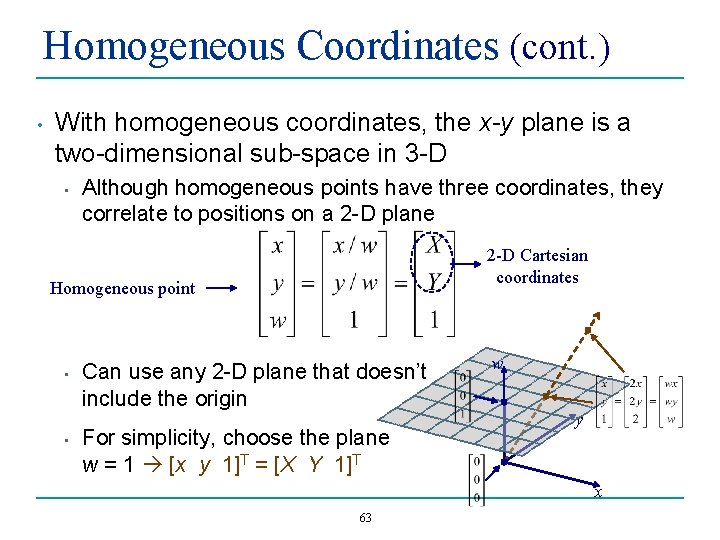
Homogeneous Coordinates (cont. ) • With homogeneous coordinates, the x-y plane is a two-dimensional sub-space in 3 -D • Although homogeneous points have three coordinates, they correlate to positions on a 2 -D plane 2 -D Cartesian coordinates Homogeneous point • • Can use any 2 -D plane that doesn’t include the origin For simplicity, choose the plane w = 1 [x y 1]T = [X Y 1]T w y x 63

Homogeneous Coordinates • For 2 D transformations, the points are now 3 vectors • And the transformation matrices are 3 x 3 matrices 64

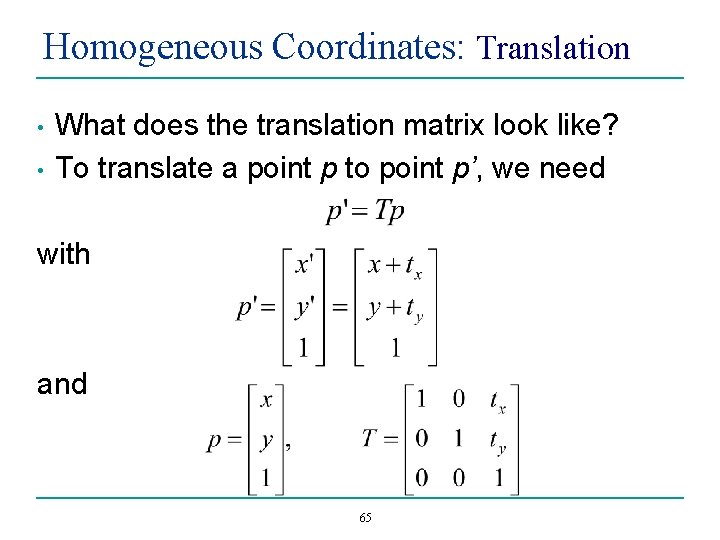
Homogeneous Coordinates: Translation • • What does the translation matrix look like? To translate a point p to point p’, we need with and 65

Homogeneous Coordinates: Scale • • What does the scale matrix look like? To scale a point p to point p’, we need with and 66

Homogeneous Coordinates: Rotation • Rotation has a similar derivation. Remember the 2 D rotation matrix: • When we move to homogeneous coordinates, we have • We apply this matrix to each vertex of a polygon to rotate the polygon as a whole 67

Composition: Rotation About a Point y arbitrary point T: Now let’s try that rotation about 5 an 1. Translate to origin: p´ = T 1 p 4 3 2 1 0 0 2. x 1 2 3 4 5 4 Rotate about origin: p´ = RT 1 p 3 2 5 1 0 0 y 4 3. 3 Translate back: p´ = T 2 RT 1 p 2 1 0 0 68 y x 1 2 3 4 q = 45° x 1 2 3 4

Composition: Rotation About a Point • So • Where M is the composite transformation matrix 69

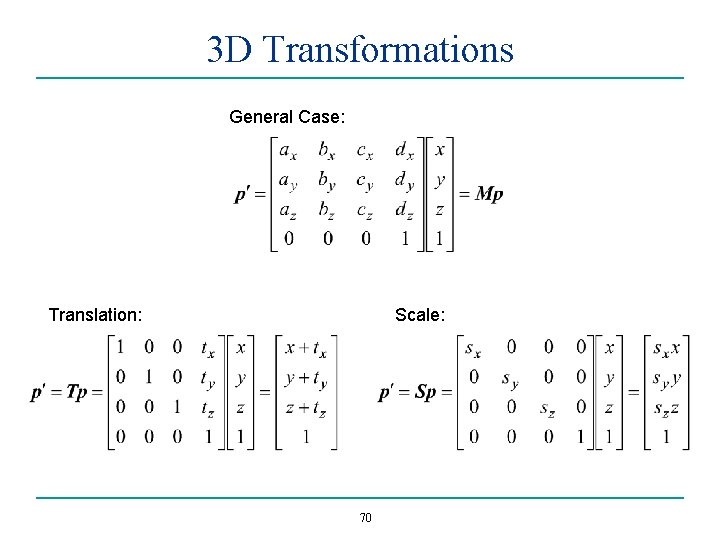
3 D Transformations General Case: Translation: Scale: 70

3 D Rotation Rotate about x-axis Rotate about y-axis Rotate about z-axis These rotations can be combined to rotate about an arbitrary axis. 71

Viewing

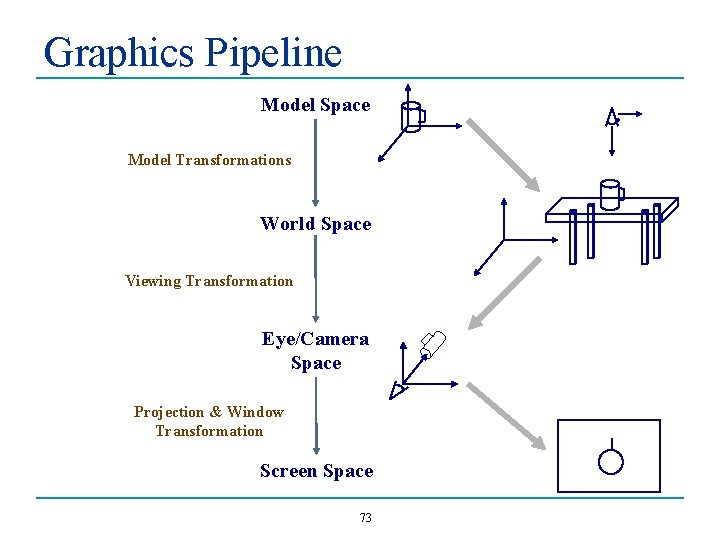
Graphics Pipeline Model Space Model Transformations World Space Viewing Transformation Eye/Camera Space Projection & Window Transformation Screen Space 73

Viewing Transformations • • Projection: take a point from m dimensions to n dimensions where n < m There are essentially two types of viewing transforms: • • Orthographic: parallel projection • Points project directly onto the view plane • In eye/camera space (after viewing transformation): drop z Perspective: convergent projection • • Points project through the origin onto the view plane In eye/camera space (after viewing transformation): divide by z 74

Projection Environment • We will use a right-handed view system y • The eye or camera position is on the +z axis, a distance d from the origin. d x • The view direction is parallel to the z axis • The view plane is in the xy plane and passes through the origin 75 z

Parallel Projection • Looking down the y axis: (x, y, z) (x’, y’, z’) x z • So z’ = 0, x’ = x 76

Parallel Projection • Thus, for parallel, orthographic projections, x’ = x, y’ = y, z’ = 0 • So, to perform a parallel projection on an object, we can use matrix multiplication What is M? i. e. , we simply drop the z coordinate 77

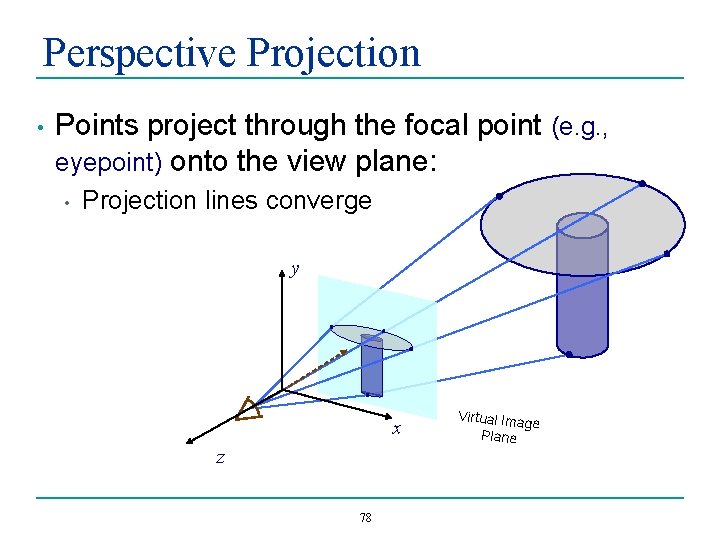
Perspective Projection • Points project through the focal point (e. g. , eyepoint) onto the view plane: • Projection lines converge y x z 78 Virtual Imag e Plane

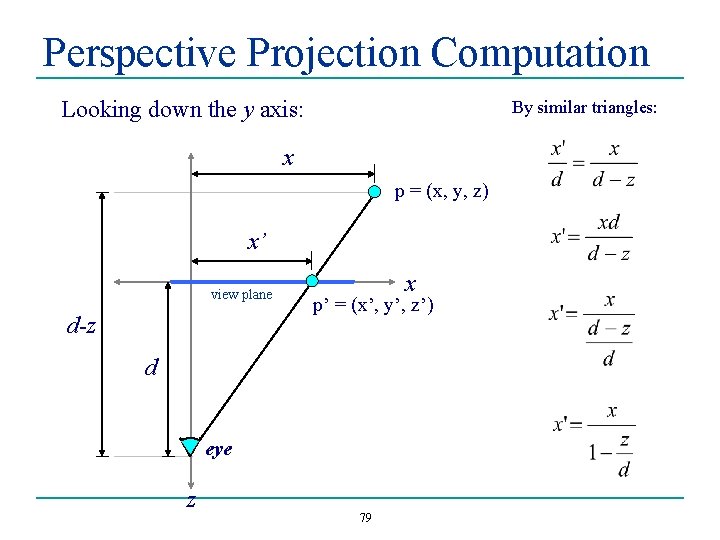
Perspective Projection Computation Looking down the y axis: By similar triangles: x p = (x, y, z) x’ view plane d-z x p’ = (x’, y’, z’) d eye z 79

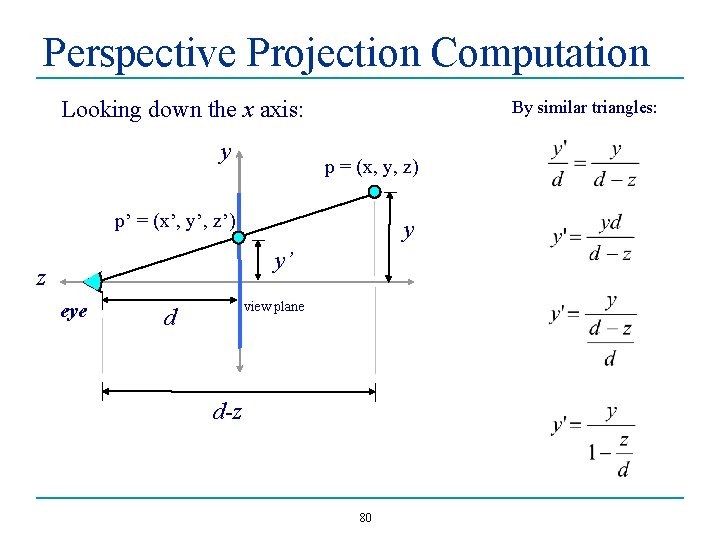
Perspective Projection Computation Looking down the x axis: y By similar triangles: p = (x, y, z) p’ = (x’, y’, z’) y y’ z eye view plane d d-z 80

Perspective Projection Computation • So, we have • what is z’? • can we put this into matrix form? 81

Perspective Projection Computation • So, the matrix that will give us the correct perspective is: This works - what is the problem with it? Answer: The entries in the matrix are point dependent! i. e. , every point will have to have a different matrix 82

Perspective Projection Computation • • Solution: use homogeneous points (remember them? ) Our Cartesian point is: • A homogeneous point that is equivalent to our desired Cartesian point is: • can we come up with a matrix that gives us what we need, but is point independent? 83

Perspective Projection Computation • We want: so, 84

Perspective Projection Computation • So, the new matrix we get is: This gives us correct results, and is point independent 85