Polygon overlay in double precision arithmetic One example

Polygon overlay in double precision arithmetic One example of why robust geometric code is hard to write Jack Snoeyink & Andrea Mantler Computer Science, UNC Chapel Hill

Outline n Motivating problems – Clipping, polygon ops, overlay, arrangement – Study precision required by algorithm n Quick summary of algorithms – Test pairs, sweep, topological sweep n A double-precision sweep algorithm – “Spaghetti” segments n Conclusions

Three problems in the plane n n n Polygon clipping (graphics) Boolean operations (CAD) Map overlay (GIS)
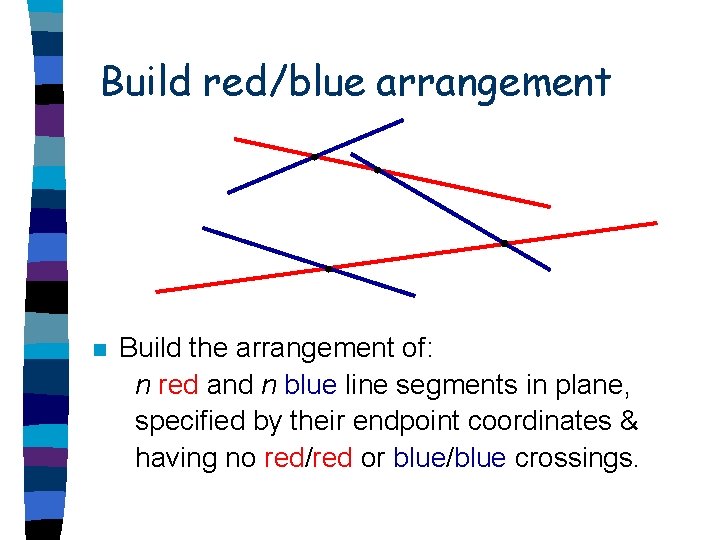
Build red/blue arrangement n Build the arrangement of: n red and n blue line segments in plane, specified by their endpoint coordinates & having no red/red or blue/blue crossings.
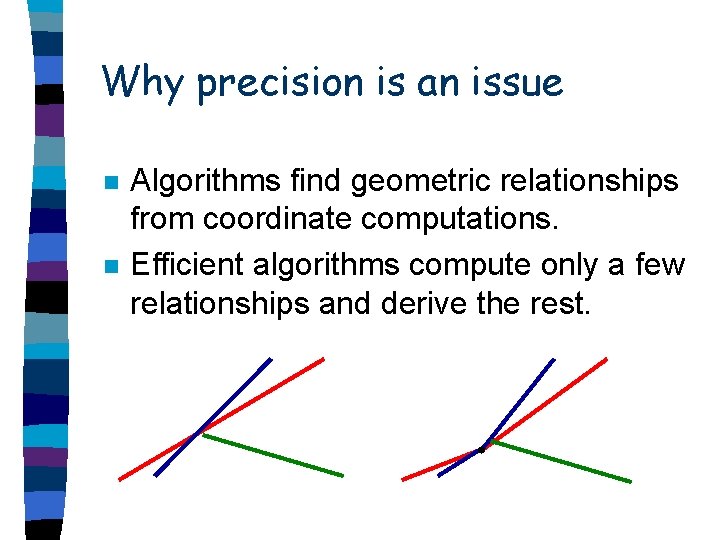
Why precision is an issue n n Algorithms find geometric relationships from coordinate computations. Efficient algorithms compute only a few relationships and derive the rest.

Assumptions & Goal n Assumptions for correctness – Solve the exact problem given by the input – Work for any distribution of the input n Goal: Input+output sensitive algorithm – Demand least precision possible – O(n log n + k) for n segs, k intersections

Algorithms to build line segment arrangements n Brute force: test all pairs Sweep the plane with a line [BO 79, C 92] Topological sweep [CE 92] Divide & Conquer [B 95] n Trapezoid sweep [C 94] n n n
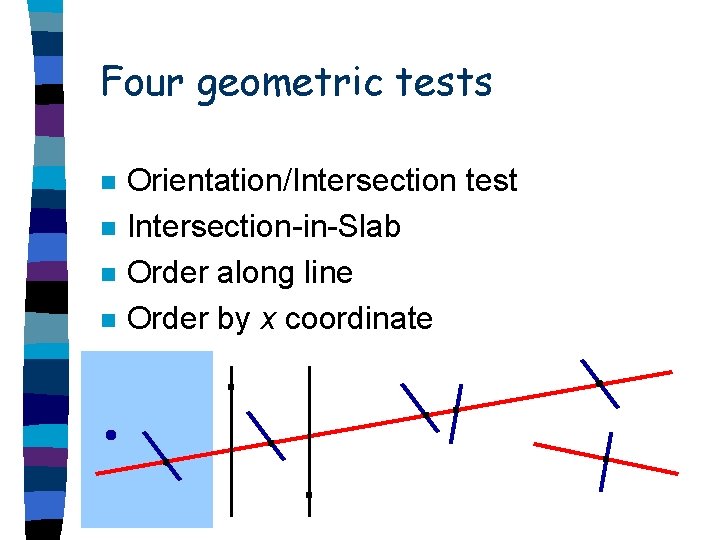
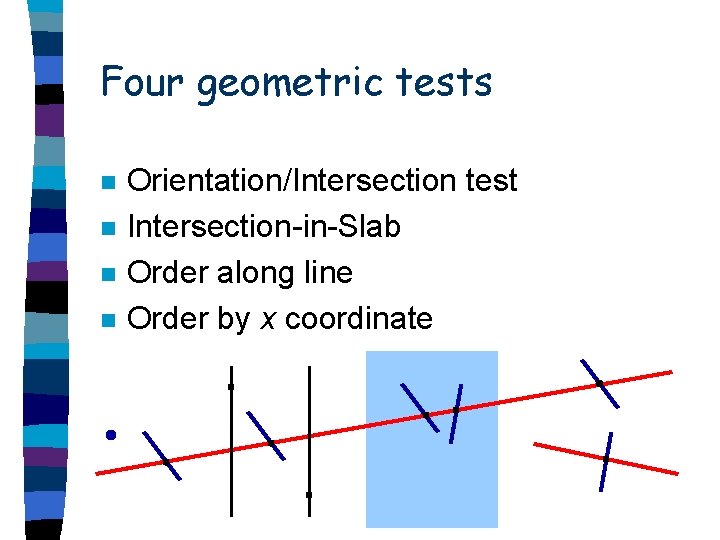
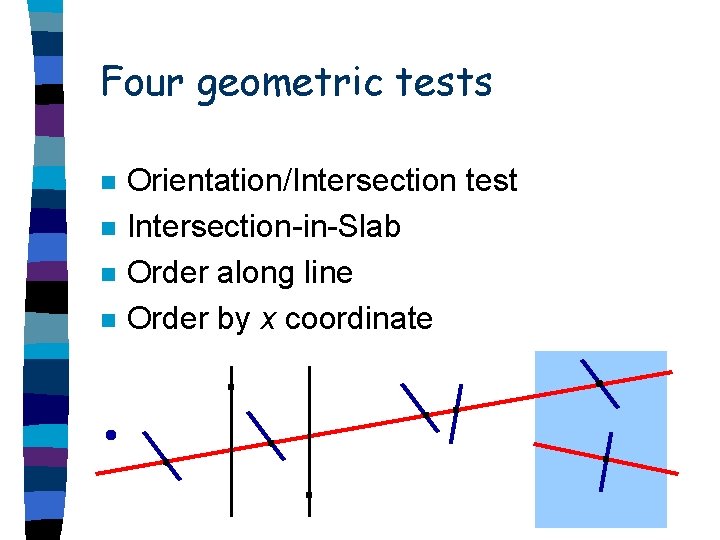
Four geometric tests n n Orientation/Intersection test Intersection-in-Slab Order along line Order by x coordinate
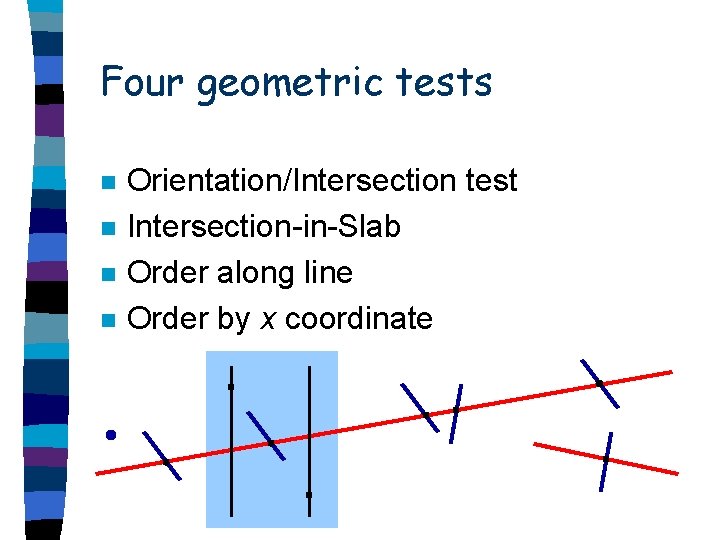
Four geometric tests n n Orientation/Intersection test Intersection-in-Slab Order along line Order by x coordinate
Four geometric tests n n Orientation/Intersection test Intersection-in-Slab Order along line Order by x coordinate
Four geometric tests n n Orientation/Intersection test Intersection-in-Slab Order along line Order by x coordinate

Algorithms to build line segment arrangements n n Brute force: test all pairs Sweep the plane with a line [BO 79, C 92] Topological sweep [CE 92] Divide & Conquer [B 95]
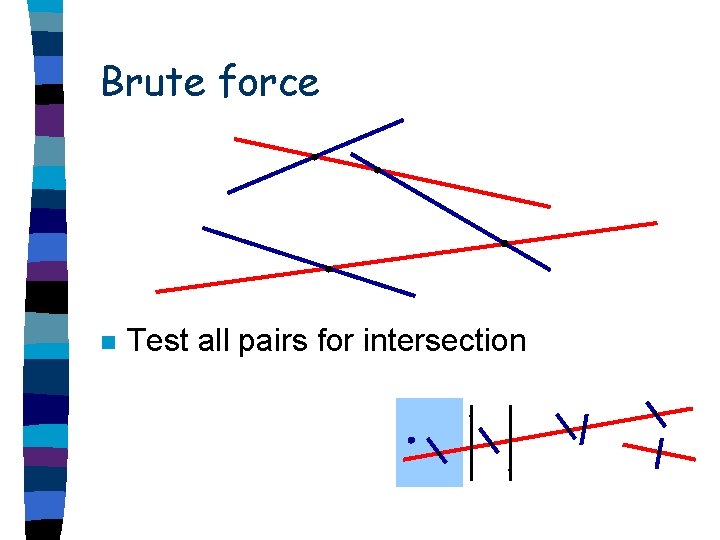
Brute force n Test all pairs for intersection
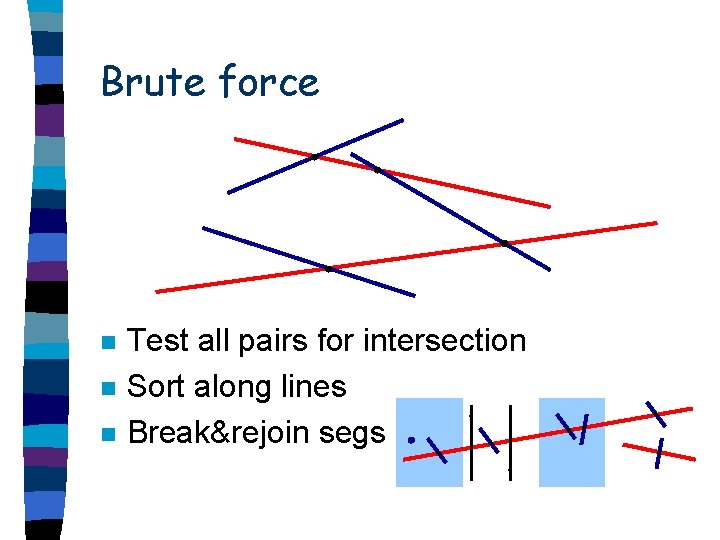
Brute force n n n Test all pairs for intersection Sort along lines Break&rejoin segs
![Plane sweep n [BO 79, C 92] Maintain order along sweep line Plane sweep n [BO 79, C 92] Maintain order along sweep line](http://slidetodoc.com/presentation_image_h2/d65e8bb0fe1712f11425e18df747d558/image-15.jpg)
Plane sweep n [BO 79, C 92] Maintain order along sweep line
![Plane sweep n [BO 79, C 92] Maintain order along sweep line Plane sweep n [BO 79, C 92] Maintain order along sweep line](http://slidetodoc.com/presentation_image_h2/d65e8bb0fe1712f11425e18df747d558/image-16.jpg)
Plane sweep n [BO 79, C 92] Maintain order along sweep line
![Plane sweep n n n [BO 79, C 92] Maintain order along sweep line Plane sweep n n n [BO 79, C 92] Maintain order along sweep line](http://slidetodoc.com/presentation_image_h2/d65e8bb0fe1712f11425e18df747d558/image-17.jpg)
Plane sweep n n n [BO 79, C 92] Maintain order along sweep line Know all intersections behind Next event queue
![Plane sweep n n n [BO 79, C 92] Maintain order along sweep line Plane sweep n n n [BO 79, C 92] Maintain order along sweep line](http://slidetodoc.com/presentation_image_h2/d65e8bb0fe1712f11425e18df747d558/image-18.jpg)
Plane sweep n n n [BO 79, C 92] Maintain order along sweep line Know all intersections behind Next event queue
![Plane sweep n n n [BO 79, C 92] Maintain order along sweep line Plane sweep n n n [BO 79, C 92] Maintain order along sweep line](http://slidetodoc.com/presentation_image_h2/d65e8bb0fe1712f11425e18df747d558/image-19.jpg)
Plane sweep n n n [BO 79, C 92] Maintain order along sweep line Know all intersections behind Next event queue
![Plane sweep n n n [BO 79, C 92] Maintain order along sweep line Plane sweep n n n [BO 79, C 92] Maintain order along sweep line](http://slidetodoc.com/presentation_image_h2/d65e8bb0fe1712f11425e18df747d558/image-20.jpg)
Plane sweep n n n [BO 79, C 92] Maintain order along sweep line Know all intersections behind Next event queue
![Plane sweep n n n [BO 79, C 92] Maintain order along sweep line Plane sweep n n n [BO 79, C 92] Maintain order along sweep line](http://slidetodoc.com/presentation_image_h2/d65e8bb0fe1712f11425e18df747d558/image-21.jpg)
Plane sweep n n n [BO 79, C 92] Maintain order along sweep line Know all intersections behind Next event queue
![Plane sweep n n n [BO 79, C 92] Maintain order along sweep line Plane sweep n n n [BO 79, C 92] Maintain order along sweep line](http://slidetodoc.com/presentation_image_h2/d65e8bb0fe1712f11425e18df747d558/image-22.jpg)
Plane sweep n n n [BO 79, C 92] Maintain order along sweep line Know all intersections behind Next event queue
![Plane sweep n n n [BO 79, C 92] Maintain order along sweep line Plane sweep n n n [BO 79, C 92] Maintain order along sweep line](http://slidetodoc.com/presentation_image_h2/d65e8bb0fe1712f11425e18df747d558/image-23.jpg)
Plane sweep n n n [BO 79, C 92] Maintain order along sweep line Know all intersections behind Next event queue
![Topological sweep n n [CE 92] Maintain order along sweep curve Know all intersections Topological sweep n n [CE 92] Maintain order along sweep curve Know all intersections](http://slidetodoc.com/presentation_image_h2/d65e8bb0fe1712f11425e18df747d558/image-24.jpg)
Topological sweep n n [CE 92] Maintain order along sweep curve Know all intersections behind
![Topological sweep n n n [CE 92] Maintain order along sweep curve Know all Topological sweep n n n [CE 92] Maintain order along sweep curve Know all](http://slidetodoc.com/presentation_image_h2/d65e8bb0fe1712f11425e18df747d558/image-25.jpg)
Topological sweep n n n [CE 92] Maintain order along sweep curve Know all intersections behind “ 20 easy pieces”
![Divide and Conquer n [B 95] Find intersections in slab with staircase Divide and Conquer n [B 95] Find intersections in slab with staircase](http://slidetodoc.com/presentation_image_h2/d65e8bb0fe1712f11425e18df747d558/image-26.jpg)
Divide and Conquer n [B 95] Find intersections in slab with staircase
![Divide and Conquer n n [B 95] Find intersections in slab with staircase Remove Divide and Conquer n n [B 95] Find intersections in slab with staircase Remove](http://slidetodoc.com/presentation_image_h2/d65e8bb0fe1712f11425e18df747d558/image-27.jpg)
Divide and Conquer n n [B 95] Find intersections in slab with staircase Remove staircase
![Divide and Conquer n n n [B 95] Find intersections in slab with staircase Divide and Conquer n n n [B 95] Find intersections in slab with staircase](http://slidetodoc.com/presentation_image_h2/d65e8bb0fe1712f11425e18df747d558/image-28.jpg)
Divide and Conquer n n n [B 95] Find intersections in slab with staircase Remove staircase Partition & repeat
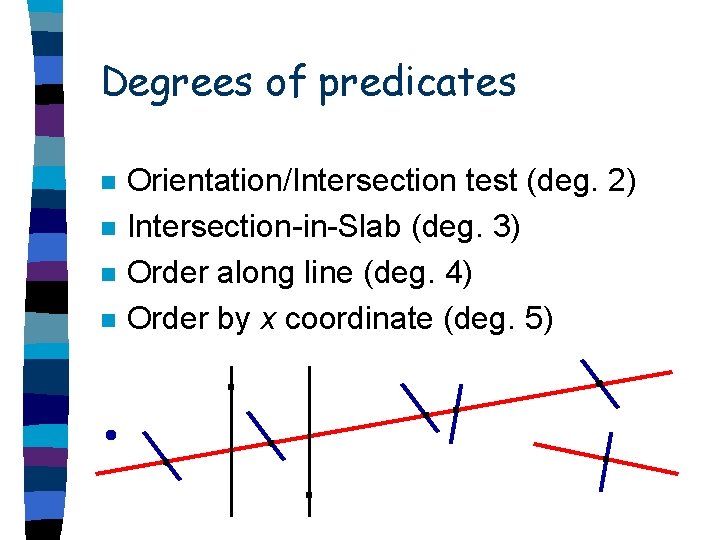
Degrees of predicates n n Orientation/Intersection test (deg. 2) Intersection-in-Slab (deg. 3) Order along line (deg. 4) Order by x coordinate (deg. 5)

Degree computations n n Point p = (1, px, py) = ((0), (1)) Line equation through points p, q:

Degree computations n n n Point p = (1, px, py) = ((0), (1)) Line equation: (2)W+(1)X+(1)Y Point at intersection of two lines:

Degree computations n n n Point p = (1, px, py) = ((0), (1)) Line equation: (2)W+(1)X+(1)Y Point at intersection ((2), (3)) ØOrientation Test: (2)(0)+(1)(1) = (2) ØIn Slab: (1) < (3)/(2) or (2)(1) < (3) = (3) ØSame Line: (2)(2) + (1)(3) = (4) Øx Order: (3)/(2) < (3)/(2) or (5)<(5) = (5)

Degree of algorithms to build line segment arrangements n n n Brute force (2/4) Sweep with a line (5) Topological sweep (4) Divide & Conquer (3/4) Trapezoid sweep (3) Restrict to double precision
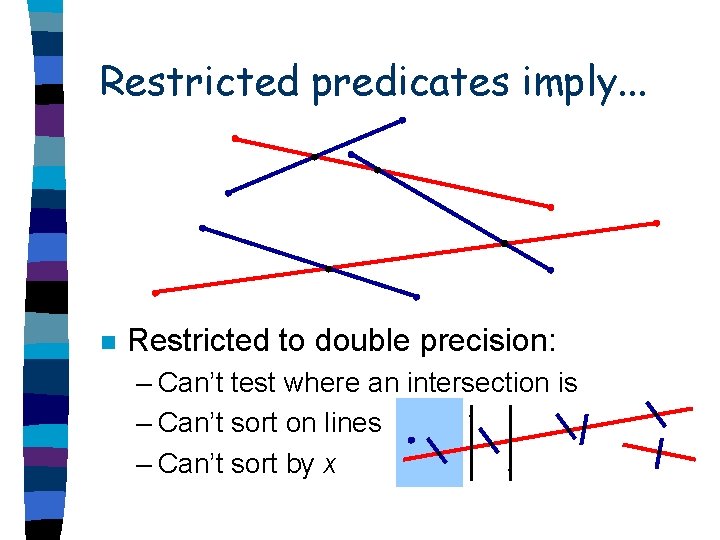
Restricted predicates imply. . . n Restricted to double precision: – Can’t test where an intersection is – Can’t sort on lines – Can’t sort by x
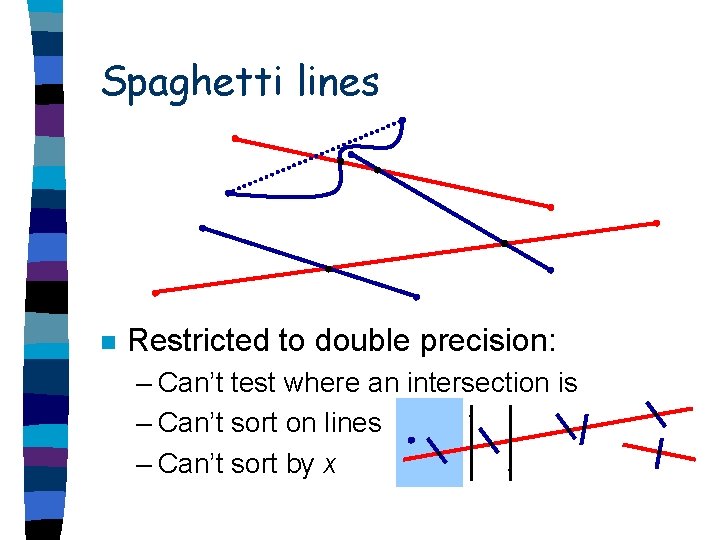
Spaghetti lines n Restricted to double precision: – Can’t test where an intersection is – Can’t sort on lines – Can’t sort by x
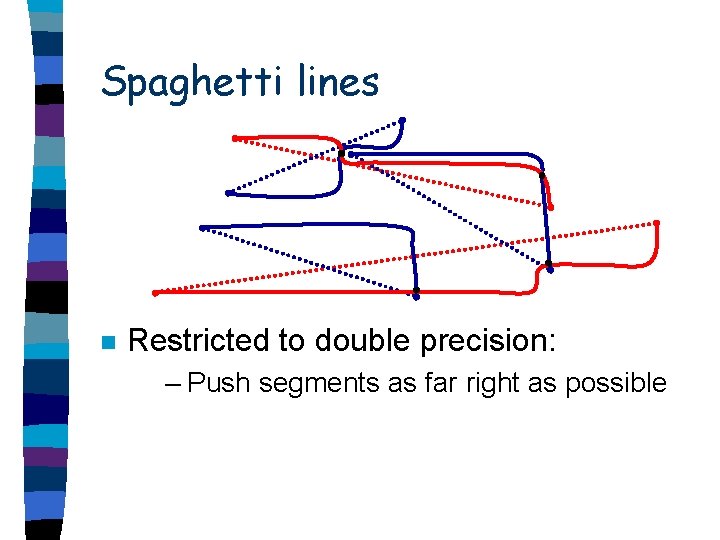
Spaghetti lines n Restricted to double precision: – Push segments as far right as possible
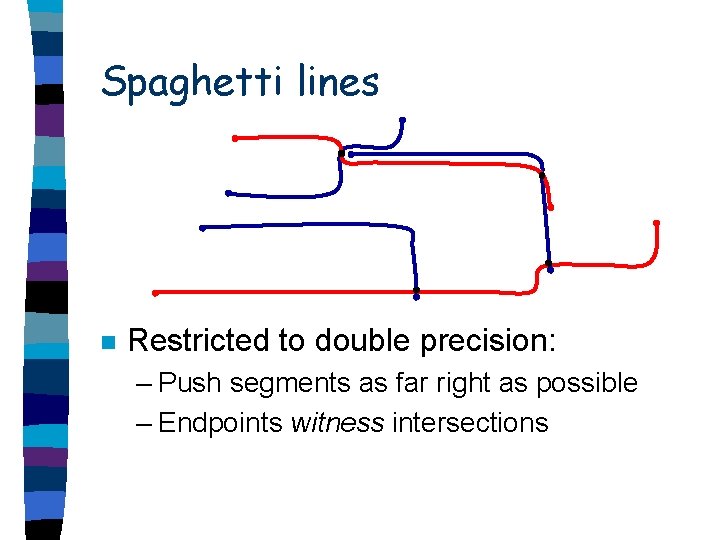
Spaghetti lines n Restricted to double precision: – Push segments as far right as possible – Endpoints witness intersections
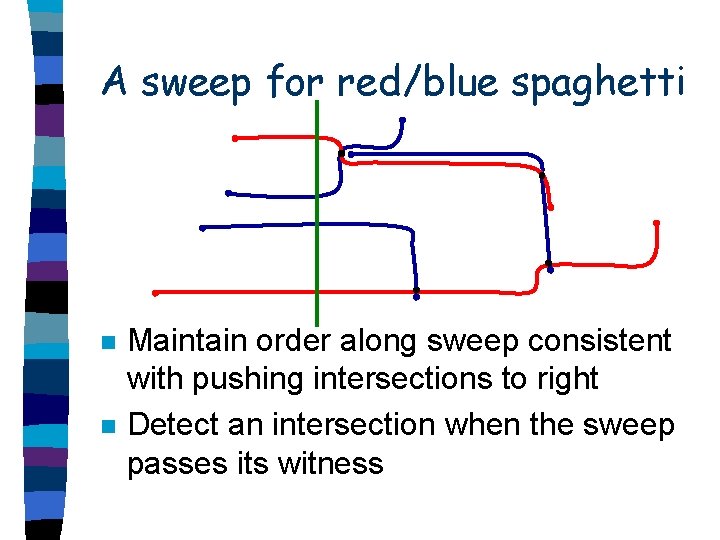
A sweep for red/blue spaghetti n n Maintain order along sweep consistent with pushing intersections to right Detect an intersection when the sweep passes its witness

Data Structures n Sweep line:
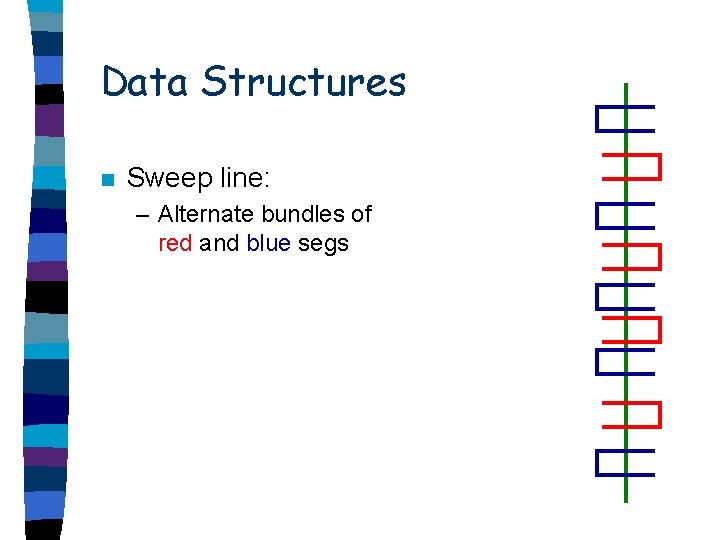
Data Structures n Sweep line: – Alternate bundles of red and blue segs
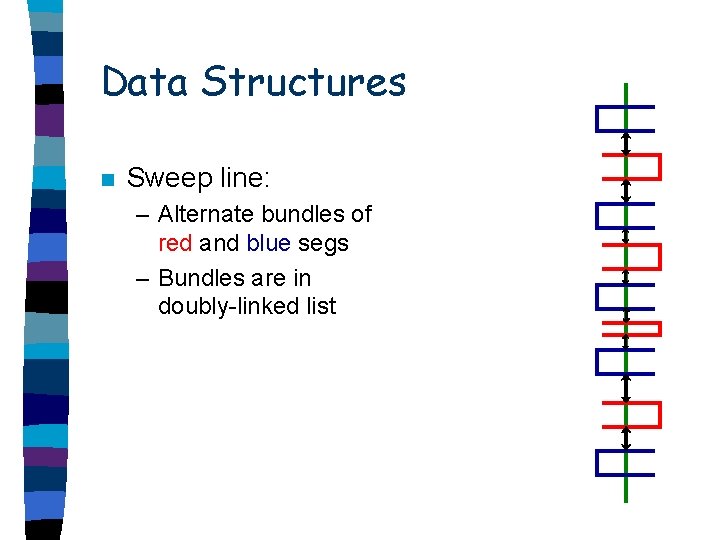
Data Structures n Sweep line: – Alternate bundles of red and blue segs – Bundles are in doubly-linked list
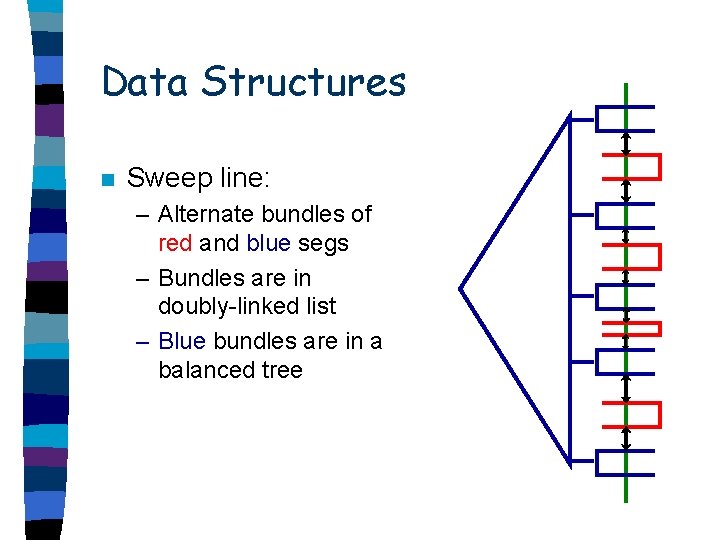
Data Structures n Sweep line: – Alternate bundles of red and blue segs – Bundles are in doubly-linked list – Blue bundles are in a balanced tree
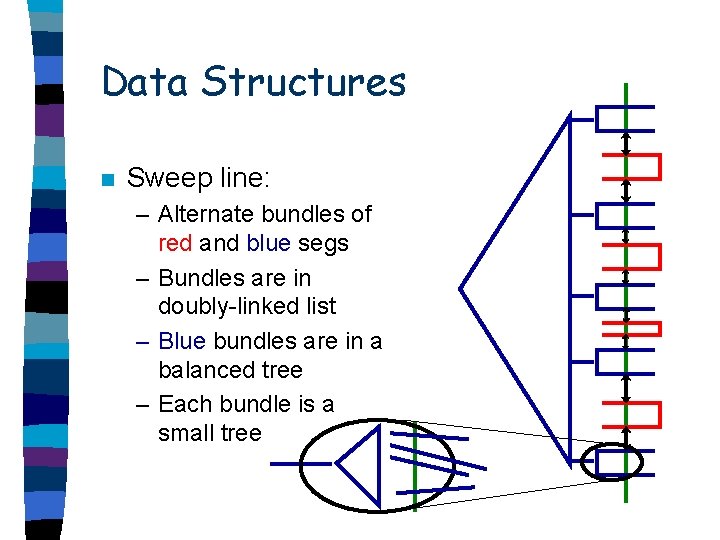
Data Structures n Sweep line: – Alternate bundles of red and blue segs – Bundles are in doubly-linked list – Blue bundles are in a balanced tree – Each bundle is a small tree
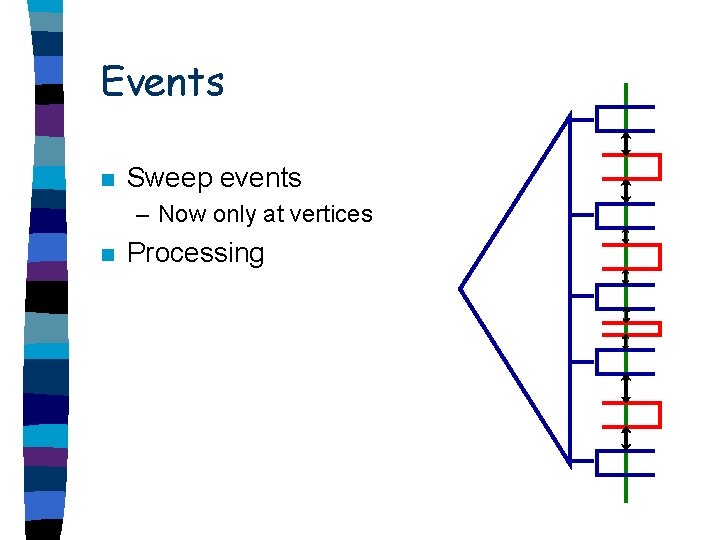
Events n Sweep events – Now only at vertices n Processing
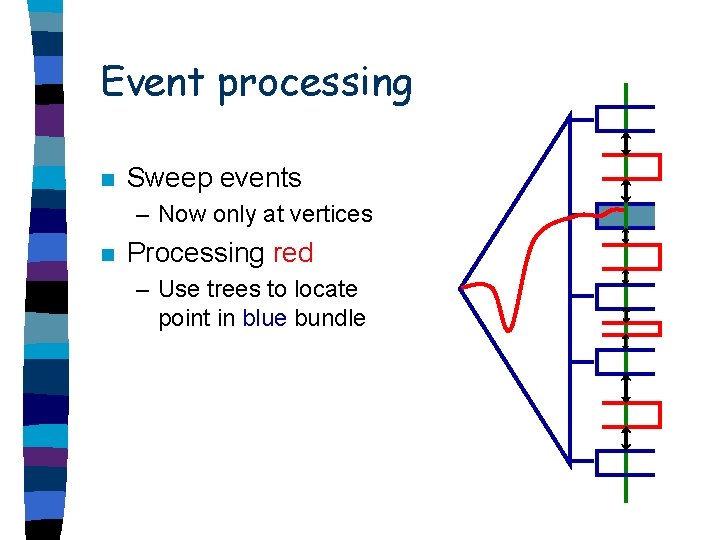
Event processing n Sweep events – Now only at vertices n Processing red – Use trees to locate point in blue bundle
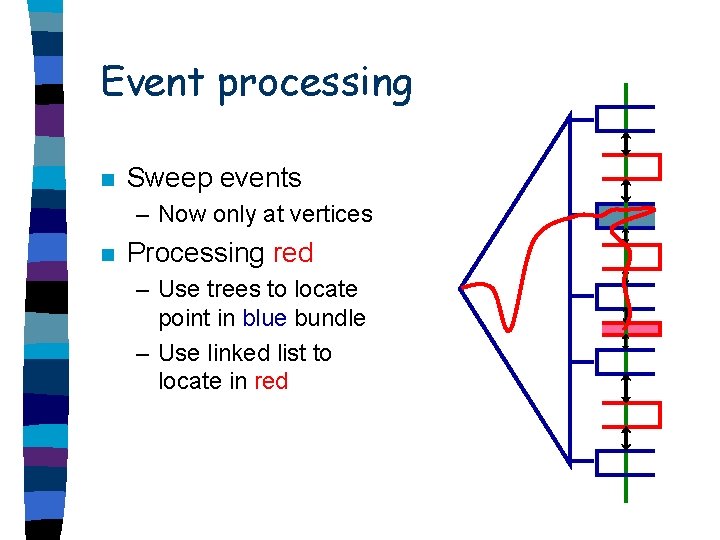
Event processing n Sweep events – Now only at vertices n Processing red – Use trees to locate point in blue bundle – Use linked list to locate in red
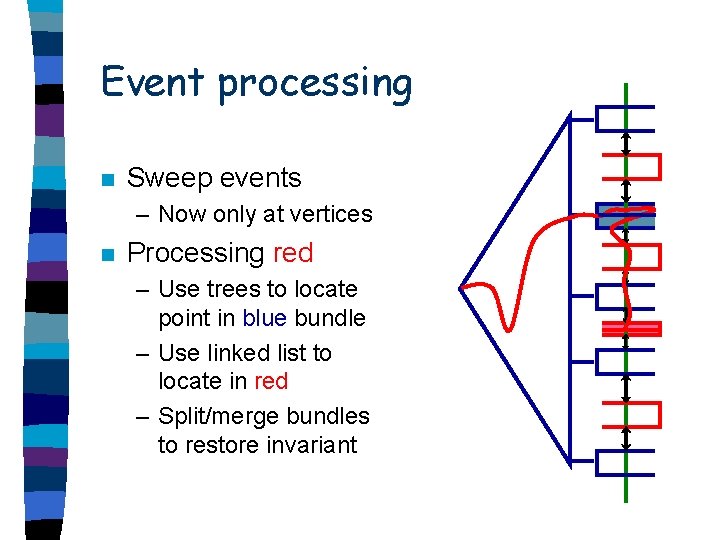
Event processing n Sweep events – Now only at vertices n Processing red – Use trees to locate point in blue bundle – Use linked list to locate in red – Split/merge bundles to restore invariant
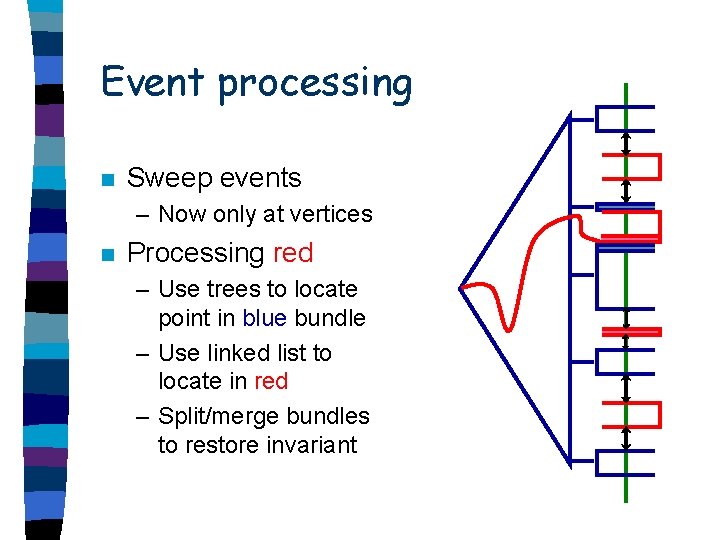
Event processing n Sweep events – Now only at vertices n Processing red – Use trees to locate point in blue bundle – Use linked list to locate in red – Split/merge bundles to restore invariant
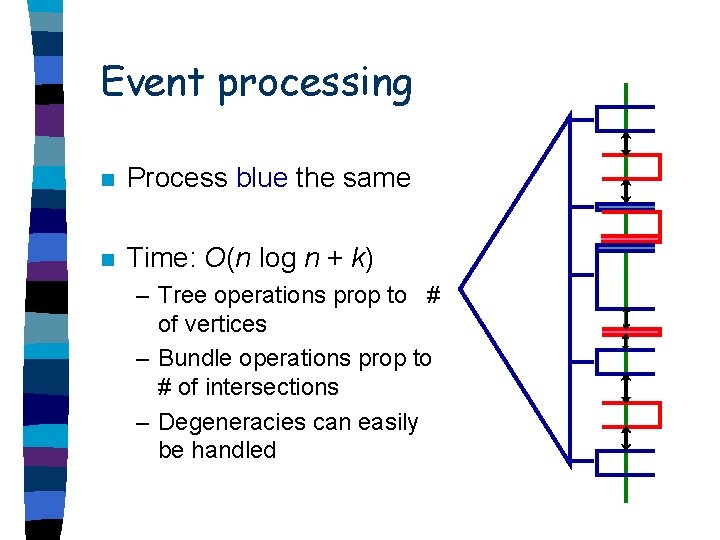
Event processing n Process blue the same n Time: O(n log n + k) – Tree operations prop to # of vertices – Bundle operations prop to # of intersections – Degeneracies can easily be handled
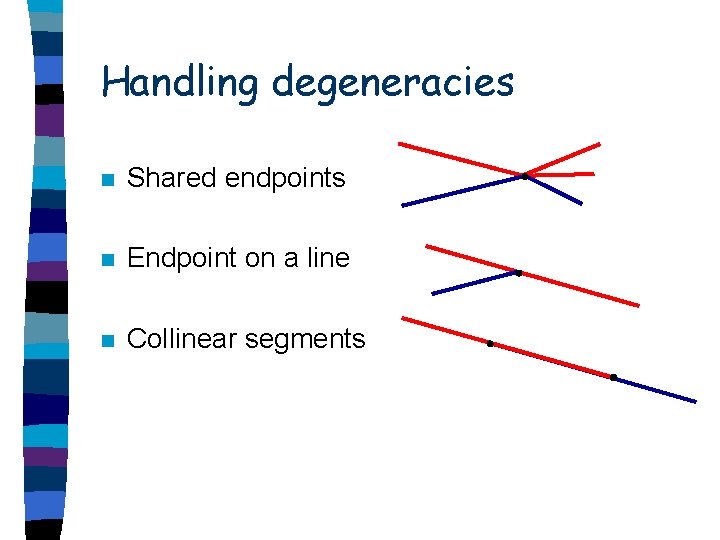
Handling degeneracies n Shared endpoints n Endpoint on a line n Collinear segments

Handling degeneracies n Shared endpoints n Endpoint on a line n Collinear segments Introduce vertices, since they are exact

Algorithm Summary n n We have an optimal algorithm to build an arrangement of red/blue segments, (and only for red/blue segments). We used only the orientation predicate. Data structuring is moderate. Can handle point/line degeneracies: breaking lines at input points is OK.
Demo applet www. cs. unc. edu/ ~snoeyink/ demos/ rbseg/
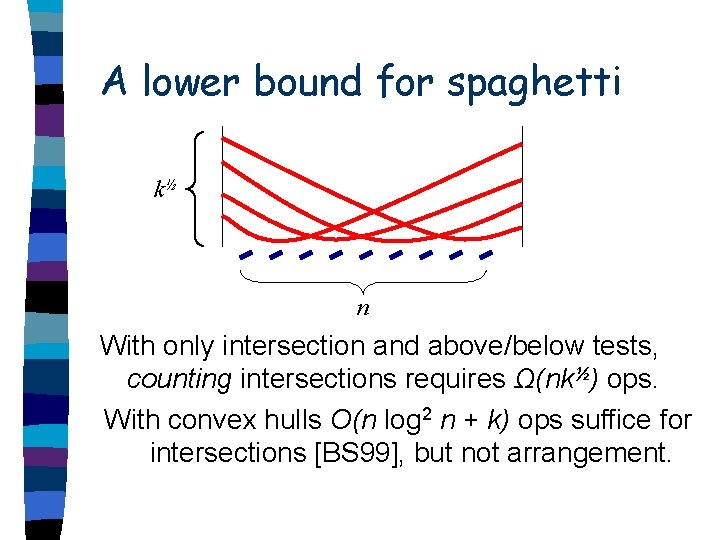
A lower bound for spaghetti k½ n With only intersection and above/below tests, counting intersections requires Ω(nk½) ops. With convex hulls O(n log 2 n + k) ops suffice for intersections [BS 99], but not arrangement.

Open question n How do we perform geometric rounding to take output back to single precision? – probably dependant on application domain – snap rounding is one idea
Fin
- Slides: 56