Politecnico di Milano Dep of Structural Engineering Center

Politecnico di Milano Dep. of Structural Engineering Center for Advanced Research and Studies in Sardinia Ludwig Maximilians University Dep. of Earth and Environmental Sciences - Geophysics THE SPECTRAL ELEMENT METHOD AS AN EFFECTIVE TOOL FOR SOLVING LARGE SCALE DYNAMIC SOIL-STRUCTURE INTERACTION PROBLEMS M. Stupazzini, C. Zambelli, L. Massidda, L. Scandella R. Paolucci, F. Maggio, C. di Prisco 20 th of April 2006 San Francisco

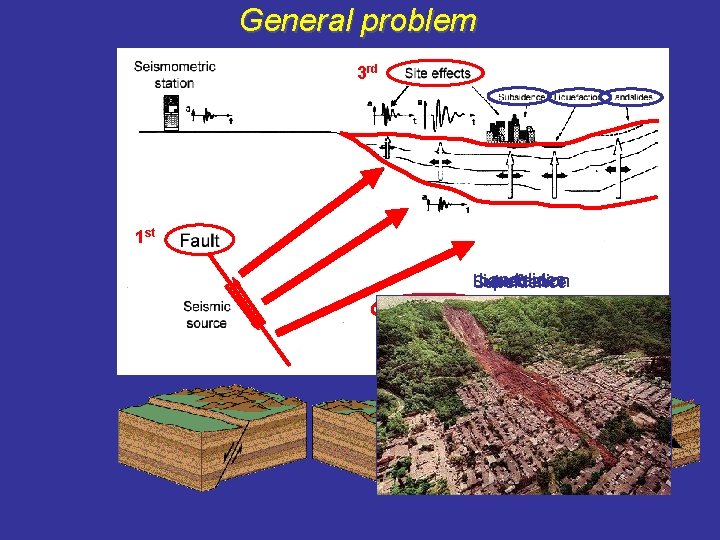
General problem 3 rd 1 st Landslides Liquefaction Subsidence 2 nd

Outlook Geo. ELSE DRM Study case

Geo. ELSE (GEO-ELasticity by Spectral Elements) • Geo. ELSE is a Spectral Elements code for the study of wave propagation phenomena in 2 D or 3 D complex domain • Developers: - CRS 4 (Center for Advanced, Research and Studies in Sardinia) - Politecnico di Milano, DIS (Department of Structural Engineering) • Native parallel implementation • Naturally oriented to large scale applications ( > at least 106 grid points)

Formulation of the elastodynamic problem Dynamic equilibrium in the weak form: where ui = unknown displacement function vi = generic admissible displacement function (test function) ti = prescribed tractions at the boundary fi = prescribed body force distribution in

Time advancing scheme Finite difference 2 nd order (LF 2 – LF 2) Courant-Friedrichs-Levy (CFL) stability condition Spatial discretization Spectral element method SEM (Faccioli et al. , 1997)

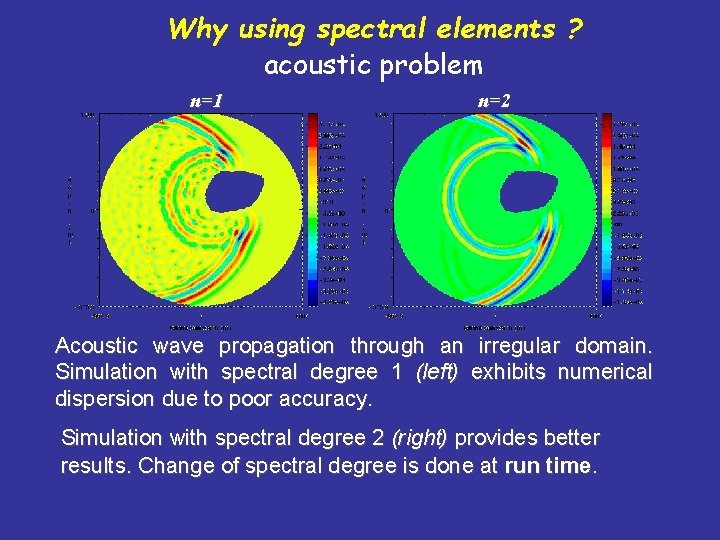
Why using spectral elements ? u Suitable for modelling a variety of physical problems (acoustic and elastic wave propagation, thermo elasticity, fluid dynamics) u Accuracy of high-order methods u Suitable for implementation in parallel architectures u Great advantages from last generation of hexahedral mesh creation program (e. g. : CUBIT, Sandia Lab. )

Why using spectral elements ? acoustic problem n=1 n=2 Acoustic wave propagation through an irregular domain. Simulation with spectral degree 1 (left) exhibits numerical dispersion due to poor accuracy. Simulation with spectral degree 2 (right) provides better results. Change of spectral degree is done at run time.

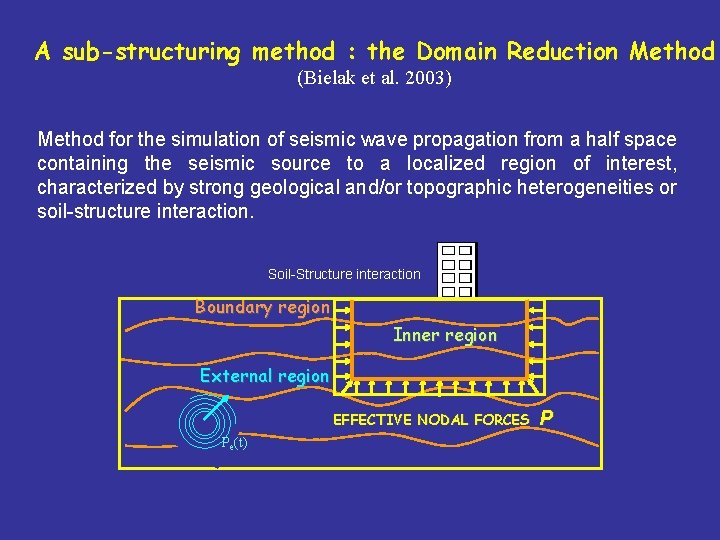
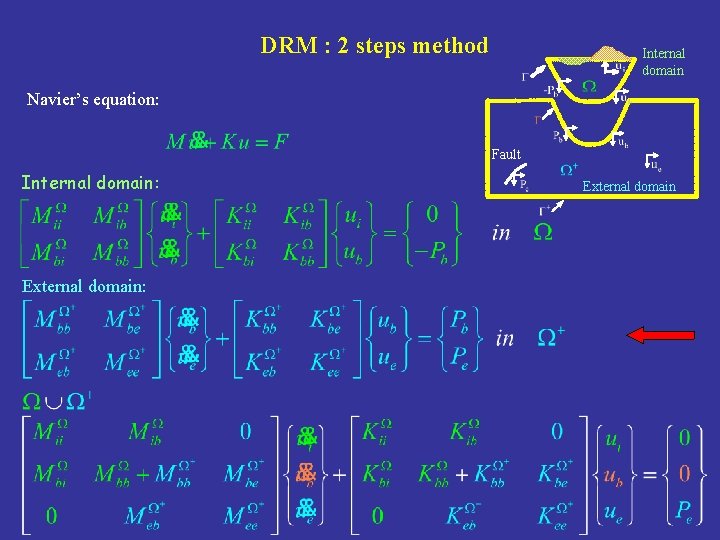
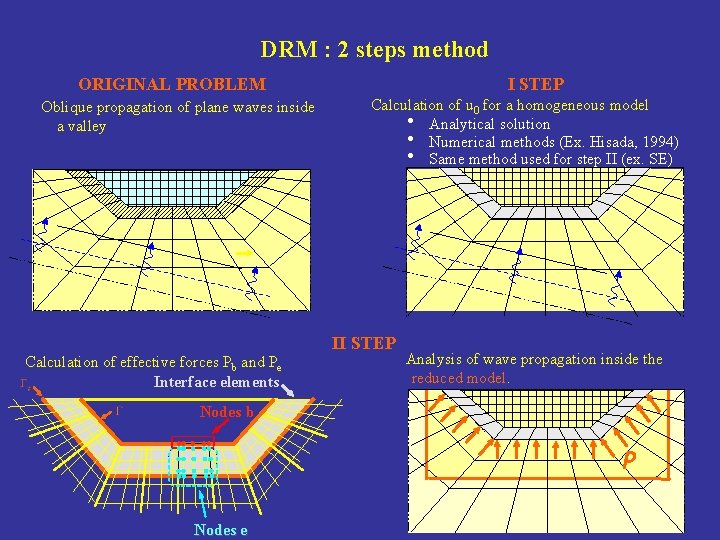
A sub-structuring method : the Domain Reduction Method (Bielak et al. 2003) Method for the simulation of seismic wave propagation from a half space containing the seismic source to a localized region of interest, characterized by strong geological and/or topographic heterogeneities or soil-structure interaction. Local geological feature interaction Soil-Structure Boundary region Inner region External region EFFECTIVE NODAL FORCES Pe(t) P

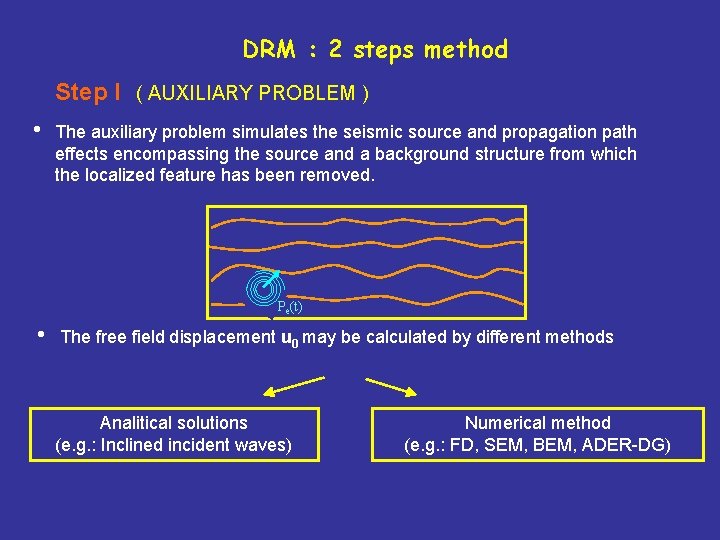
DRM : 2 steps method Step I ( AUXILIARY PROBLEM ) • The auxiliary problem simulates the seismic source and propagation path effects encompassing the source and a background structure from which the localized feature has been removed. Pe(t) • The free field displacement u 0 may be calculated by different methods Analitical solutions (e. g. : Inclined incident waves) Numerical method (e. g. : FD, SEM, BEM, ADER-DG)

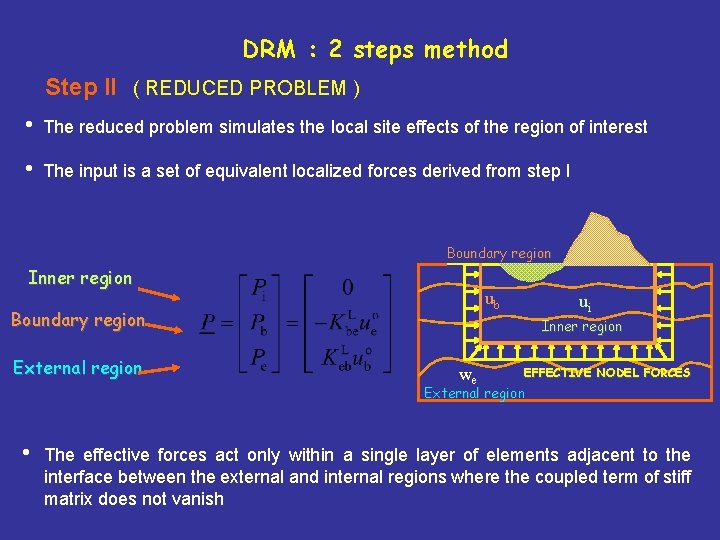
DRM : 2 steps method Step II ( REDUCED PROBLEM ) • The reduced problem simulates the local site effects of the region of interest • The input is a set of equivalent localized forces derived from step I Boundary region Inner region ub Boundary region External region ui Inner region we EFFECTIVE NODEL FORCES External region • The effective forces act only within a single layer of elements adjacent to the interface between the external and internal regions where the coupled term of stiff matrix does not vanish

Study case railway bridge

Wave propagation in 2 D “Source“ & “ Deep propagation“ zoom Fault “ Site effects “ & “ Soil Structures Interactions “ zoom

Computational comparison: Simulation # elem. Memory Dtsimulation [Mb] [sec. ] Single model 2790 15 1. 177 10 -5 # time steps Tot. CPU time [min. ] 570 620 190. 0

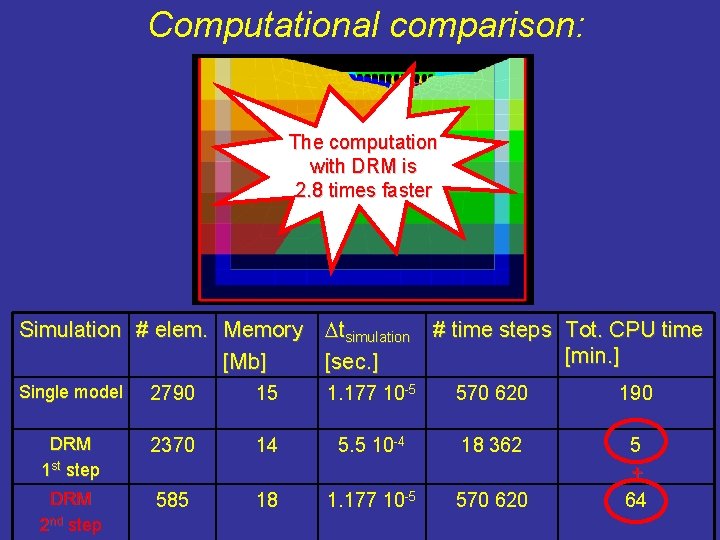
Computational comparison: Simulation # elem. Memory Dtsimulation [Mb] [sec. ] # time steps Tot. CPU time [min. ] Single model 2790 15 1. 177 10 -5 570 620 190. 0 DRM 1 st step 2370 14 5. 5 10 -4 18 362 5. 5

Computational comparison: The computation with DRM is 2. 8 times faster Simulation # elem. Memory Dtsimulation [Mb] [sec. ] # time steps Tot. CPU time [min. ] Single model 2790 15 1. 177 10 -5 570 620 190 DRM 1 st step 2370 14 5. 5 10 -4 18 362 DRM 2 nd step 585 18 1. 177 10 -5 570 620 5 + 64

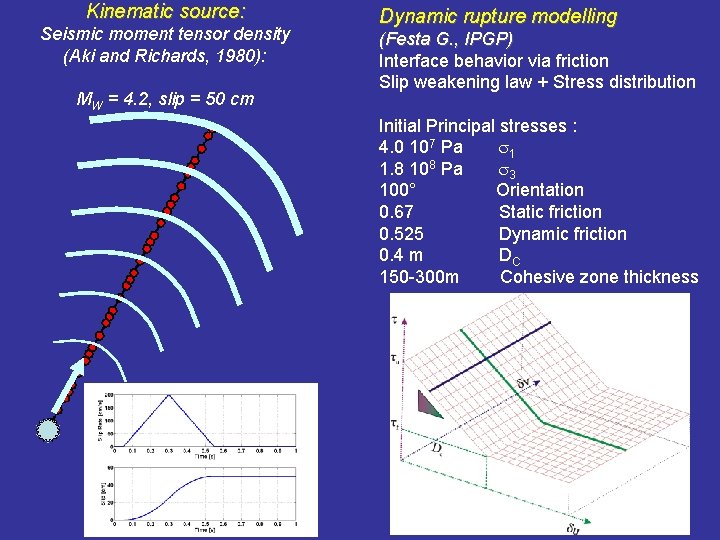
Kinematic source: Seismic moment tensor density (Aki and Richards, 1980): MW = 4. 2, slip = 50 cm Dynamic rupture modelling (Festa G. , IPGP) Interface behavior via friction Slip weakening law + Stress distribution Initial Principal stresses : 4. 0 107 Pa s 1 1. 8 108 Pa s 3 100° Orientation 0. 67 Static friction 0. 525 Dynamic friction 0. 4 m DC 150 -300 m Cohesive zone thickness

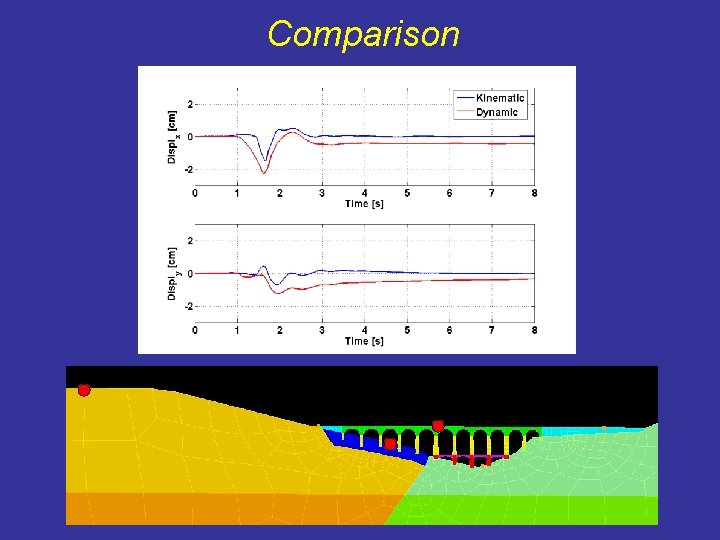
Comparison

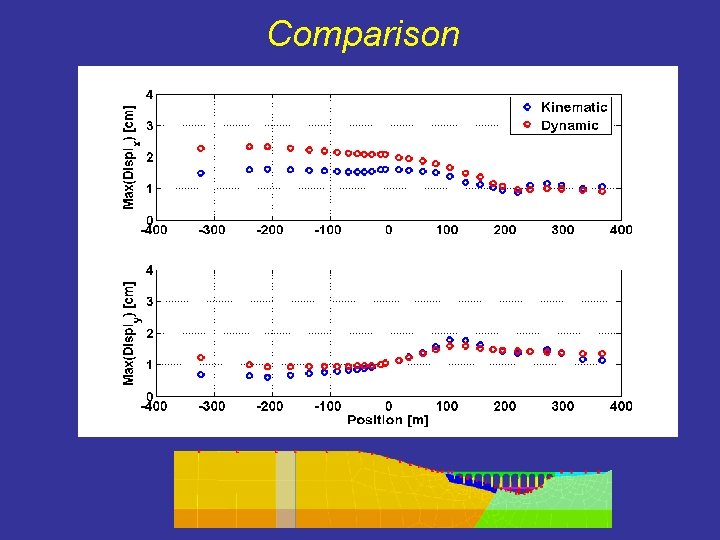
Comparison

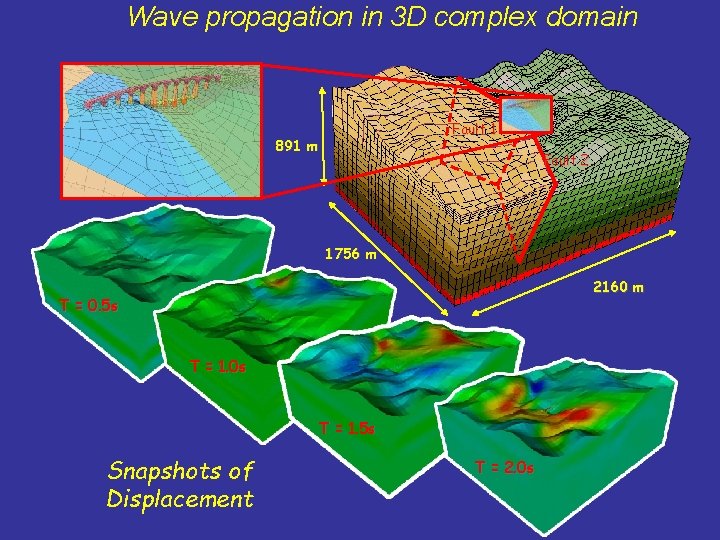
Wave propagation in 3 D complex domain Fault 1 891 m Fault 2 1756 m 2160 m T = 0. 5 s T = 1. 0 s T = 1. 5 s Snapshots of Displacement T = 2. 0 s

Conclusions • Geo. ELSE is capable to handle „source to structure“ wave propagation problem. • Thanks to DRM we acchieve: • reduced computational time • dialog between numerical codes oriented for different purposes • WEB SITE: www. stru. polimi. it/Ccosmm/ccosmm. htm www. spice-rtn. org

DRM : 2 steps method Internal domain Navier’s equation: Fault Internal domain: External domain

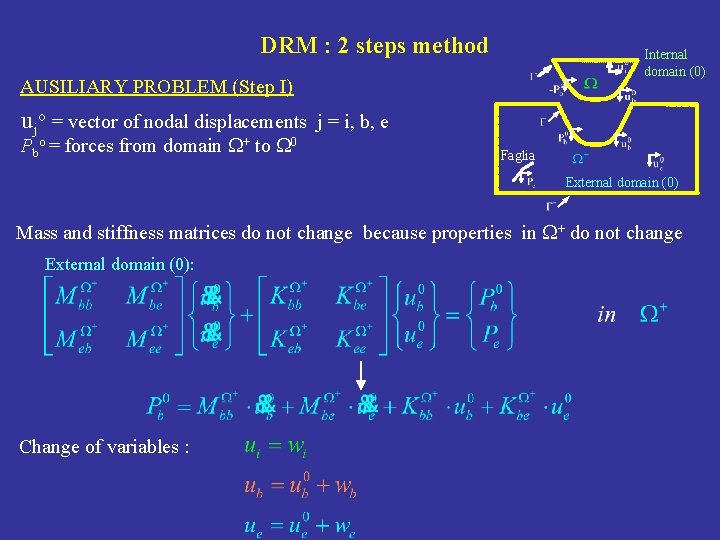
DRM : 2 steps method Internal domain (0) AUSILIARY PROBLEM (Step I) ujo = vector of nodal displacements j = i, b, e Pbo = forces from domain + to 0 Faglia External domain (0) Mass and stiffness matrices do not change because properties in + do not change External domain (0): Change of variables :

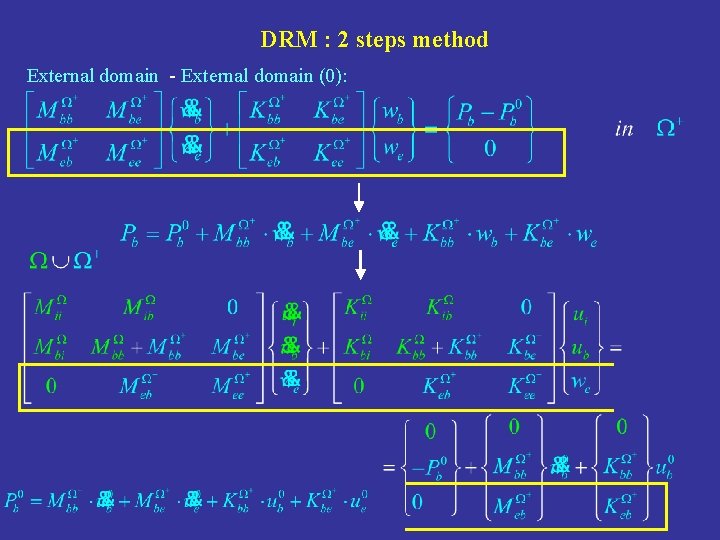
DRM : 2 steps method External domain - External domain (0): Dominio interno:

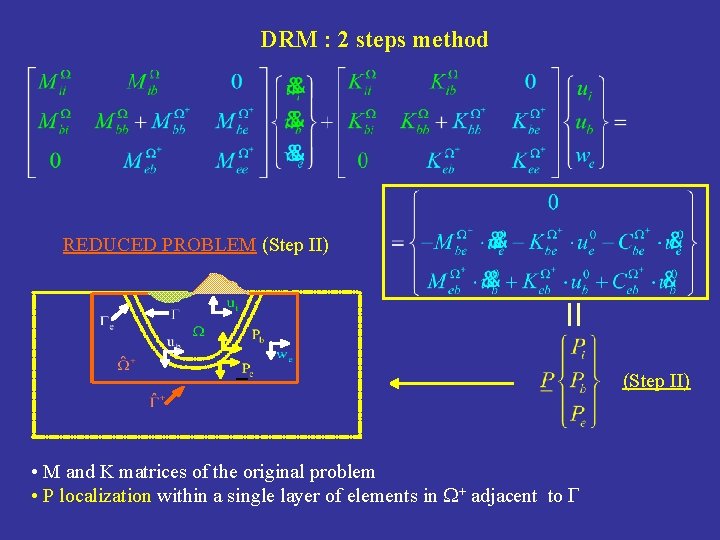
DRM : 2 steps method REDUCED PROBLEM (Step II) • M and K matrices of the original problem • P localization within a single layer of elements in + adjacent to

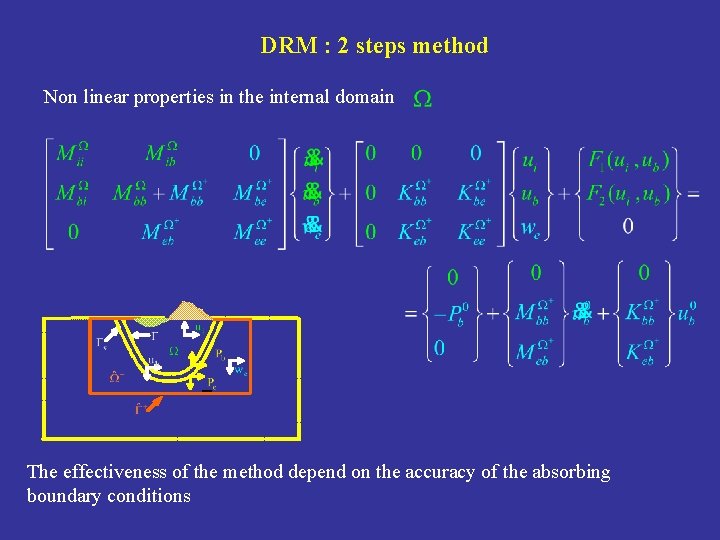
DRM : 2 steps method Non linear properties in the internal domain The effectiveness of the method depend on the accuracy of the absorbing boundary conditions

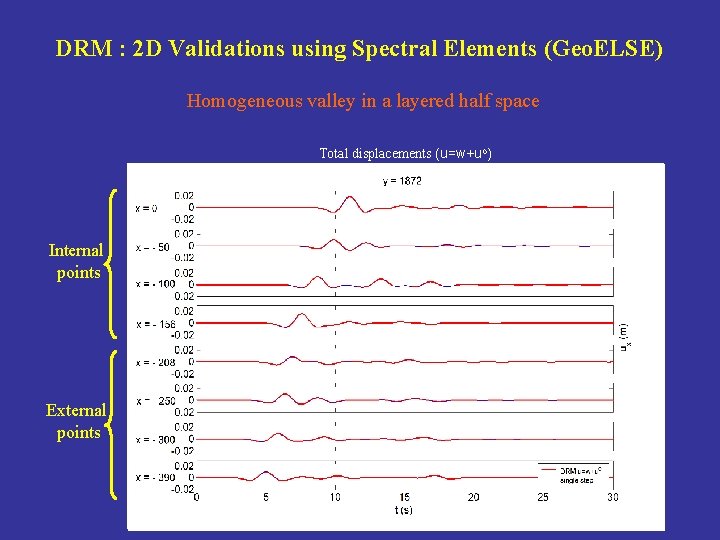
DRM : 2 D Validations using Spectral Elements (Geo. ELSE) Homogeneous valley in a layered half space Mechanical properties VS [m/s] VP [m/s] r [m/s] Valley 45 1000 50 100 1200 80 140 1600 180 1800 Half space

DRM : 2 D Validations using Spectral Elements (Geo. ELSE) Homogeneous valley in a layered half space Relative displacements (w)o) Total displacements (u=w+u Internal points External points

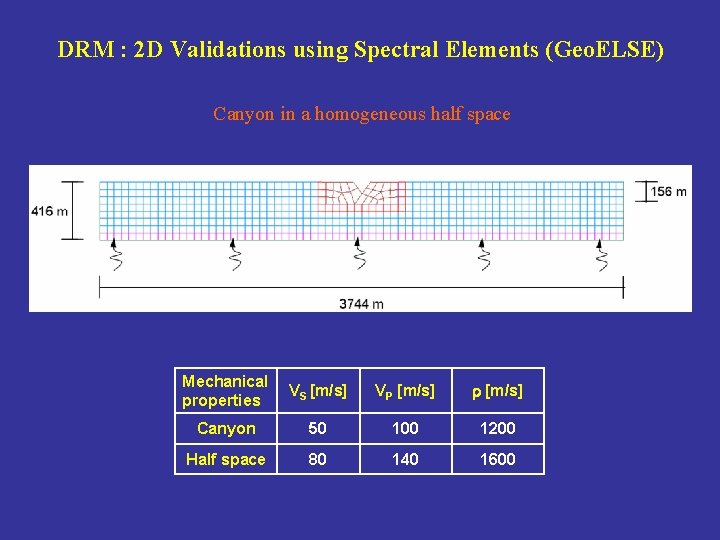
DRM : 2 D Validations using Spectral Elements (Geo. ELSE) Canyon in a homogeneous half space Mechanical properties VS [m/s] VP [m/s] r [m/s] Canyon 50 100 1200 Half space 80 140 1600

DRM : 2 D Validations using Spectral Elements (Geo. ELSE) Canyon in a homogeneous half space Relative displacements Total displacements (w) (u=w+uo) Internal points External points

DRM : 2 steps method I STEP ORIGINAL PROBLEM Oblique propagation of plane waves inside a valley Calculation of effective forces Pb and Pe Interface elements Calculation of u 0 for a homogeneous model • Analytical solution • Numerical methods (Ex. Hisada, 1994) • Same method used for step II (ex. SE) II STEP Analysis of wave propagation inside the reduced model. Nodes b P Nodes e

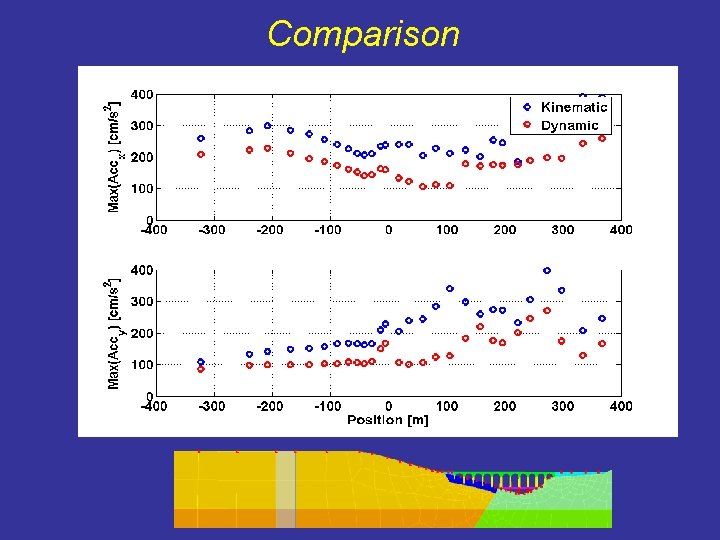
Comparison

Conclusions • Capabilities of DRM to handle „source to structure“ wave propagation problem with reduced CPU time • Dialog between numerical codes oriented for different purposes • Kinematic model are satisfactory to describe the low frequency bahaviour (e. g. : PGD and PGV) while PGA seems to be overestimated (nucleation, constant rupture velocity and instantaneous drop of the slip on the fault boundaries? ).