Politechnika Warszawska Wydzia Fizyki Przejcia fazowe w modelu

Politechnika Warszawska Wydział Fizyki Przejścia fazowe w modelu Isinga na sprzężonych sieciach złożonych Krzysztof Suchecki Janusz A. Hołyst

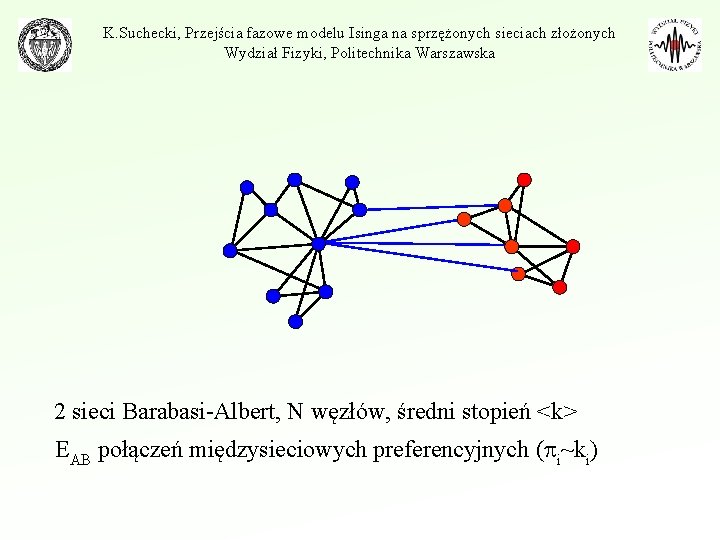
K. Suchecki, Przejścia fazowe modelu Isinga na sprzężonych sieciach złożonych Wydział Fizyki, Politechnika Warszawska 2 sieci Barabasi-Albert, N węzłów, średni stopień <k> EAB połączeń międzysieciowych preferencyjnych ( i~ki)

K. Suchecki, Przejścia fazowe modelu Isinga na sprzężonych sieciach złożonych Wydział Fizyki, Politechnika Warszawska Przybliżenie średniopolowe Zwykłe równanie samouzgodnione dla modelu Isinga Średnie połączenie i-j Samouzgodnione równanie spinu Spin ważony Samouzgodnione równanie spinu ważonego G. Bianconi, “Mean field solution of the Ising model on a Barabasi-Albert network”, Physic Letters A 303, 166 -168 (2002)

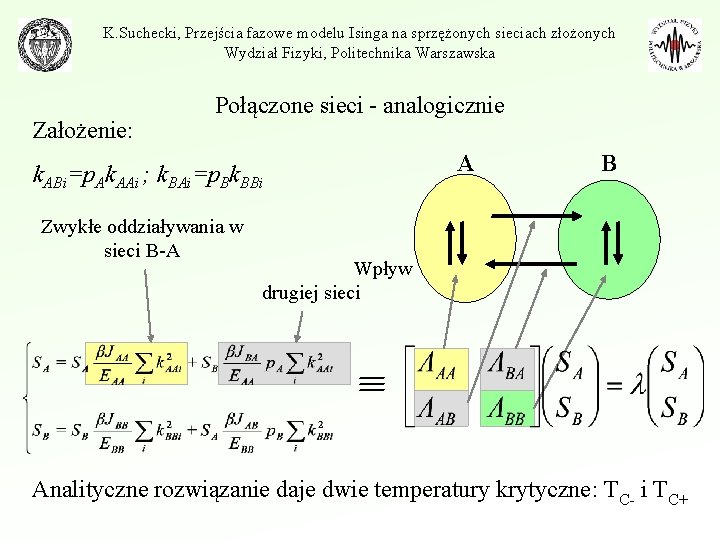
K. Suchecki, Przejścia fazowe modelu Isinga na sprzężonych sieciach złożonych Wydział Fizyki, Politechnika Warszawska Założenie: Połączone sieci - analogicznie k. ABi=p. Ak. AAi ; k. BAi=p. Bk. BBi Zwykłe oddziaływania w sieci B-A A B Wpływ drugiej sieci Analityczne rozwiązanie daje dwie temperatury krytyczne: TC- i TC+

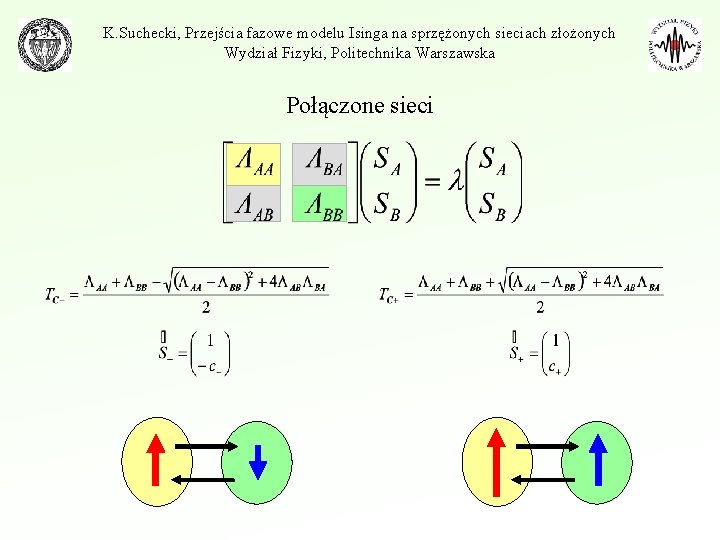
K. Suchecki, Przejścia fazowe modelu Isinga na sprzężonych sieciach złożonych Wydział Fizyki, Politechnika Warszawska Połączone sieci

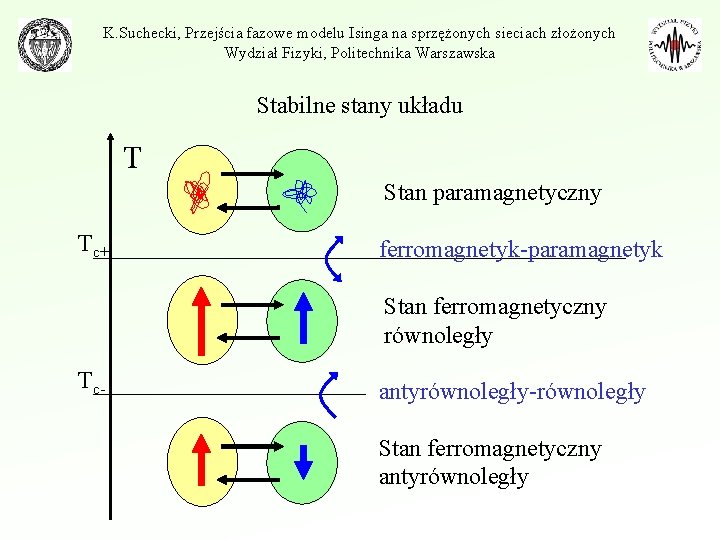
K. Suchecki, Przejścia fazowe modelu Isinga na sprzężonych sieciach złożonych Wydział Fizyki, Politechnika Warszawska Stabilne stany układu T Stan paramagnetyczny Tc+ ferromagnetyk-paramagnetyk Stan ferromagnetyczny równoległy Tc- antyrównoległy-równoległy Stan ferromagnetyczny antyrównoległy

K. Suchecki, Przejścia fazowe modelu Isinga na sprzężonych sieciach złożonych Wydział Fizyki, Politechnika Warszawska Przejścia fazowe na przykładzie sprzężonych grafów regularnych (<k>=const. ) Nie sprzężone: Tc 0 Ferromagnetyk. Paramagnetyk: Tc+ Antyrównoległy. Równoległy, przejście 1 rodzaju: Tc 1 Antyrównoległy. Równoległy: Tc-

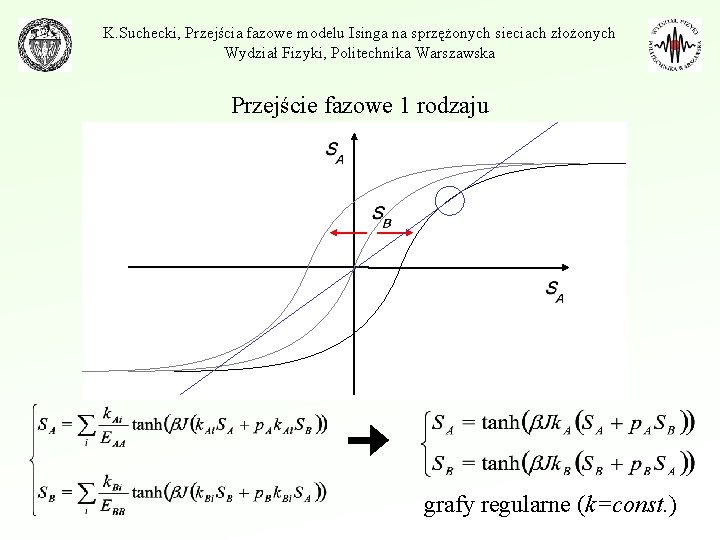
K. Suchecki, Przejścia fazowe modelu Isinga na sprzężonych sieciach złożonych Wydział Fizyki, Politechnika Warszawska Przejście fazowe 1 rodzaju grafy regularne (k=const. )

K. Suchecki, Przejścia fazowe modelu Isinga na sprzężonych sieciach złożonych Wydział Fizyki, Politechnika Warszawska Przejście fazowe 1 rodzaju Warunek niestabilności: Założenie: takie same sieci (k. A=k. B=k) Daje się wyznaczyć zależność p(T). Można odwrócić zależność graficznie, uzyskując wykres Tc 1(p).

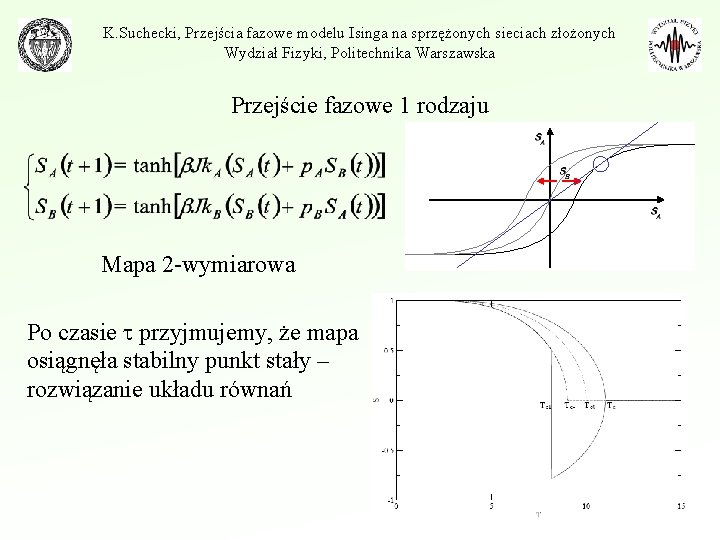
K. Suchecki, Przejścia fazowe modelu Isinga na sprzężonych sieciach złożonych Wydział Fizyki, Politechnika Warszawska Przejście fazowe 1 rodzaju Mapa 2 -wymiarowa Po czasie przyjmujemy, że mapa osiągnęła stabilny punkt stały – rozwiązanie układu równań

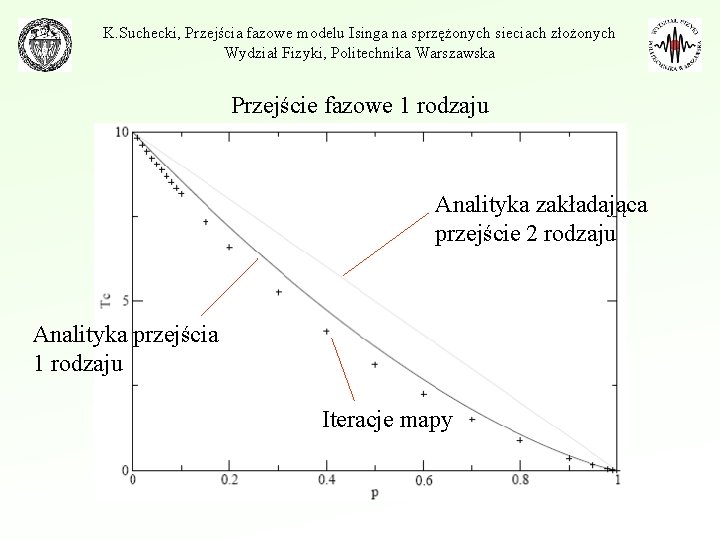
K. Suchecki, Przejścia fazowe modelu Isinga na sprzężonych sieciach złożonych Wydział Fizyki, Politechnika Warszawska Przejście fazowe 1 rodzaju Analityka zakładająca przejście 2 rodzaju Analityka przejścia 1 rodzaju Iteracje mapy

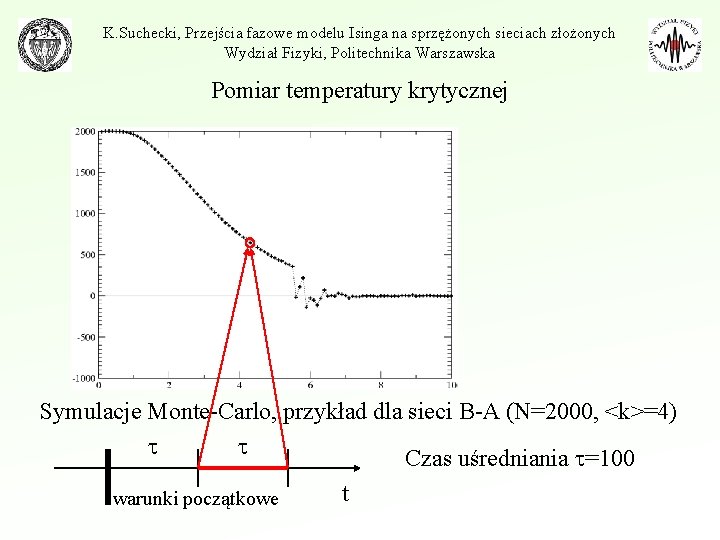
K. Suchecki, Przejścia fazowe modelu Isinga na sprzężonych sieciach złożonych Wydział Fizyki, Politechnika Warszawska Pomiar temperatury krytycznej Symulacje Monte-Carlo, przykład dla sieci B-A (N=2000, <k>=4) Czas uśredniania =100 warunki początkowe t

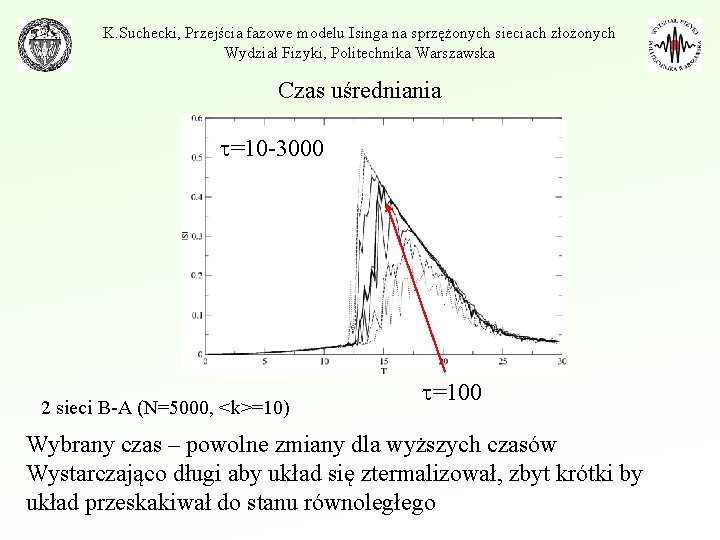
K. Suchecki, Przejścia fazowe modelu Isinga na sprzężonych sieciach złożonych Wydział Fizyki, Politechnika Warszawska Czas uśredniania =10 -3000 2 sieci B-A (N=5000, <k>=10) =100 Wybrany czas – powolne zmiany dla wyższych czasów Wystarczająco długi aby układ się ztermalizował, zbyt krótki by układ przeskakiwał do stanu równoległego

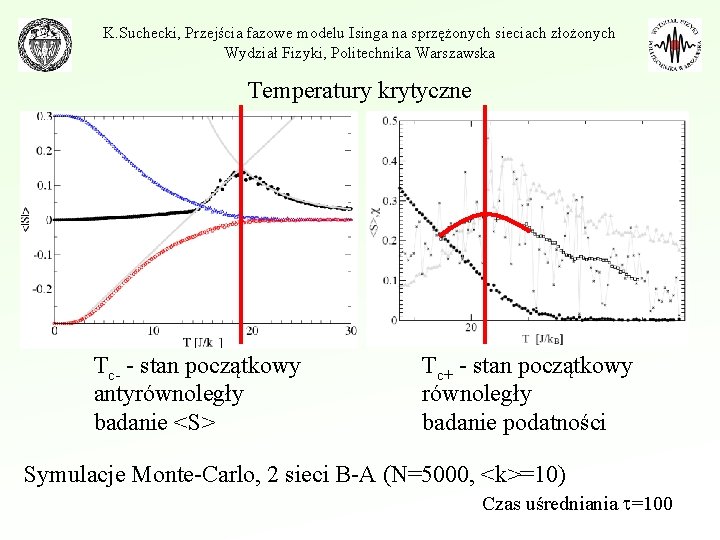
K. Suchecki, Przejścia fazowe modelu Isinga na sprzężonych sieciach złożonych Wydział Fizyki, Politechnika Warszawska Temperatury krytyczne Tc- - stan początkowy antyrównoległy badanie <S> Tc+ - stan początkowy równoległy badanie podatności Symulacje Monte-Carlo, 2 sieci B-A (N=5000, <k>=10) Czas uśredniania =100

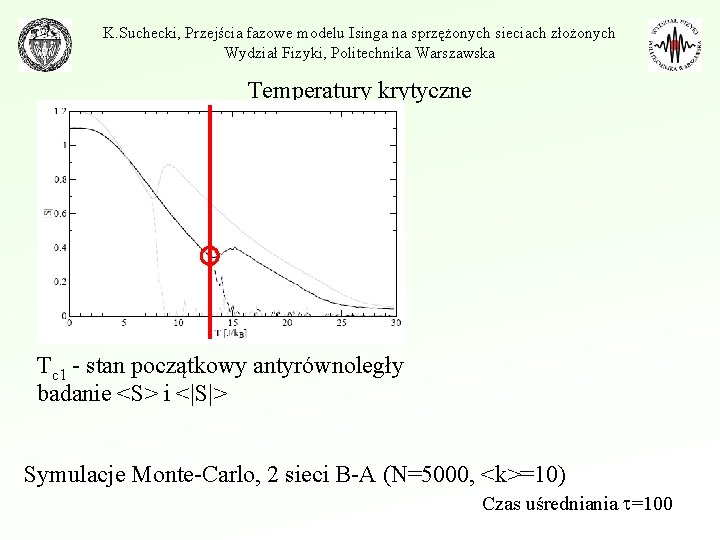
K. Suchecki, Przejścia fazowe modelu Isinga na sprzężonych sieciach złożonych Wydział Fizyki, Politechnika Warszawska Temperatury krytyczne Tc 1 - stan początkowy antyrównoległy badanie <S> i <|S|> Symulacje Monte-Carlo, 2 sieci B-A (N=5000, <k>=10) Czas uśredniania =100

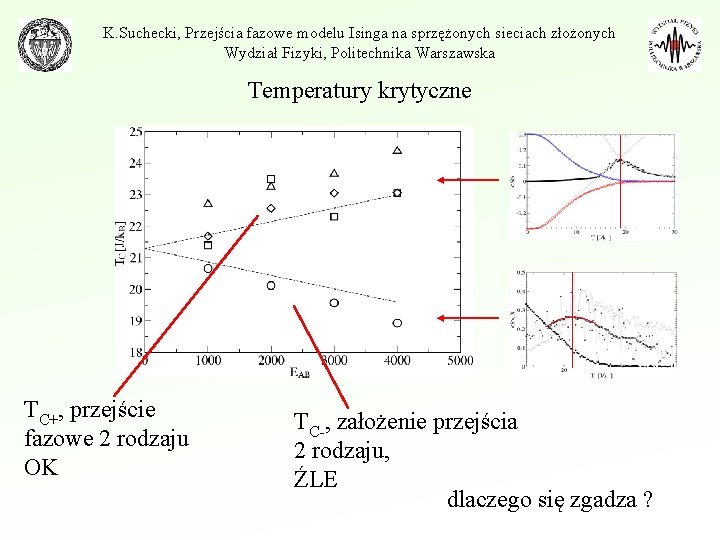
K. Suchecki, Przejścia fazowe modelu Isinga na sprzężonych sieciach złożonych Wydział Fizyki, Politechnika Warszawska Temperatury krytyczne TC+, przejście fazowe 2 rodzaju OK TC-, założenie przejścia 2 rodzaju, ŹLE dlaczego się zgadza ?

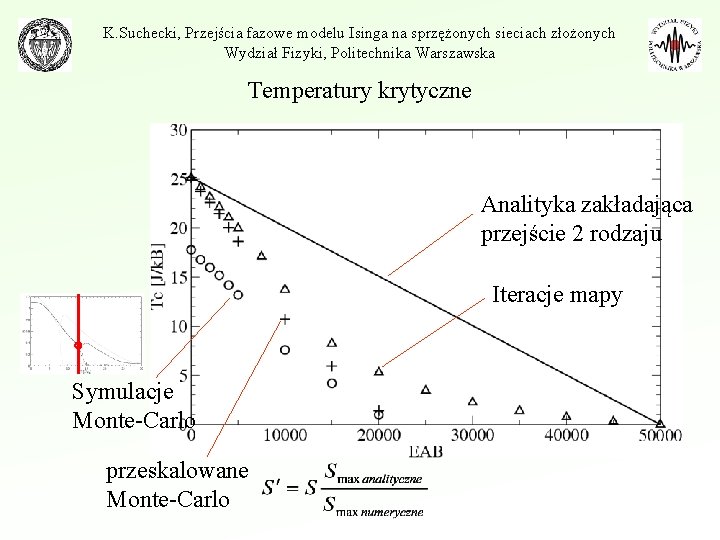
K. Suchecki, Przejścia fazowe modelu Isinga na sprzężonych sieciach złożonych Wydział Fizyki, Politechnika Warszawska Temperatury krytyczne Analityka zakładająca przejście 2 rodzaju Iteracje mapy Symulacje Monte-Carlo przeskalowane Monte-Carlo

K. Suchecki, Przejścia fazowe modelu Isinga na sprzężonych sieciach złożonych Wydział Fizyki, Politechnika Warszawska Dziękuję za uwagę K. Suchecki, J. A. Hołyst, “Ising model on two connected Barabasi-Albert networks”, Phys. Rev. E 74: 011122 (2006) K. Suchecki, J. A. Hołyst, “First order phase transition in Ising model on two connected Barabasi-Albert networks”, w przygotowaniu