Polinomial Tujuan pembelajaran 1 Menjelaskan algoritma pembagian sukubanyak

Polinomial Tujuan pembelajaran : 1. Menjelaskan algoritma pembagian sukubanyak. 2. Menentukan derajat sukubanyak hasil bagi dan sisa pembagian dalam algoritma pembagian. 3. Menentukan hasil bagi dan sisa pembagian sukubanyak oleh bentuk linear atau kuadrat. 4. Menentukan sisa pembagian sukubanyak dengan teorema sisa atau teorema faktor.

Polinomial A. Pengertian Polinomial dan Operasinya Kolah kamar mandi Andi berbentuk balok. Dengan panjang kolah adalah 2 dm lebih dari lebarnya, Sedangkan tingginya 1 dm lebih dari lebarnya. Jika kolah tersebut diisi air hingga penuh, volume Air yang mampu ditampung adalah 120 liter. Bagaimana model matematikanya? Penyelesaiannya : Misal, x = lebar kolah dan V(x) = volumenya, sehingga Panjang = x + 2 dan tinggi = x + 1 Volume = panjang x lebar x tinggi Disebut polinomial/ V(x) = (x + 2)(x)(x + 1) sukubanyak = x 3 +3 x 2 + 2 x Bentuk x 3 + 3 x 2 + 2 x

Coba : 1. (x – 1)(x + 2) = x 2 + x - 2 2. x(x – 1)(x + 2) = x(x 2 + x – 2)=x 3 + x 2 – 2 x 3. x 2 (x – 1)(x + 2) = x 2(x 2 + x – 2)=x 4 + x 3 – 2 x 2 Bentuk umum : anxn + an-1 xn-1 + an-2 xn-2 +. . . + a 2 x 2 + a 1 x + a 0 Operasi-operasi polinomial Ex 1. 1. (3 x 2 + 4 x – 1) + (2 x 4 + x 2 – 5 x + 4) 2. (3 x 2 + 4 x + 1) - (4 x 4 + x 2 + x + 3) 3. (7 x 2 + 4 x – 8) + (2 x 4 + x 2 – 5 x ) 4. (x 2 + 4 x) + (x 4 + 3 x 2 – 5 x )

Ex 2. Diketahui : p(x) = ax 2 + bx + 7 q(x) = 3 x 2 + (a + b)x 2 + (a – b)x – 8 r(x) = 3 x 3 + 7 x 2 + 2 x – 1 Jika r(x) = p(x) + q(x), tentukan nilai a dan b. Ex 3. Diketahui : Tentukan nila A dan B

Tugas 1 15 Juli 2014 1. Tentukan nilai a dan b pada sukubanyak berikut jika berlaku p(x) + q(x)= r(x). a. p(x) =4 x 5 + ax 2 + (a – 3)x + 3 q(x) = 2 x 4 – x 3 + 2 bx 2 + (2 b + 1)x + 1 r(x) = 4 x 5 + 2 x 4 – x 3 + 5 x 2 + 3 x + 4 b. p(x) =x 4 + (a + b)x 3 – 2 x 2 + x – 1 q(x) = 2 bx 3 + 2 x 2 + (a – 3 b) r(x) = x 4 + 7 x 3 + x – 6 2. Tentukan nilai a, b, dan c : a. 2 ax 2 + (a + 2 b)x + (c – 2 a) ≡ 3 x 2 – x + 8

b. 3. Tentukan hasil bagi dan sisa pembagian berikut : a. (2 x 3 + 3 x 2 + 4 x + 1) : (x + 1) b x 4 + 2 x 3 – 4 x 2 + 7 x – 4 : (x – 3)

B. Pembagian Sukubanyak 1. Pembagian Bersusun Ex. 4. Tentukan hasil bagi dan sisa dari pembagian : 2. Pembagian dengan cara Horner a. Pembagi bentuk linear ( x – k ) Bentuk : f(x) = ( x – k ) H(x) + S Misal : Maka hasil baginya : Sisa : dibagi ( x – k )

Ex. 5. Tentukan hasil bagi dan sisa dari pembagian : b. Pembagi bentuk linear ( ax + k ) Ex. 6. Tentukan hasil bagi dan sisa dari pembagian :

c. Pembagi bentuk kuadrat ax 2 + bx + c, a ≠ 0 Ex. 7. Tentukan hasil bagi dan sisa dari pembagian 2 x 4 – 4 x 3 + 11 x 2 – 3 x + 9 oleh x 2 – 2 x + 3 Sehingga : f(x) = (x 2 – 2 x + 3)H(x) + (px + q) C. Teorema Sisa Jika sukubanyak P(x) berderajat n dibagi ( x – h ) maka sisa pembagiannya adalah P(h) Bukti : pandang P(x) = ( x – h ). H(x) + S Dengan x – h = 0 atau x = h, diperoleh : P(h) = 0. H(h) + S P(h) = 0 + S S = P(h)

Ex. 7. Tentukan sisa dari pembagian sukubanyak P(x) = x 2 – 6 x – 8 dengan x + 1. Ex. 8. Jika sukubanyak f(x) dibagi ( x – 1 ) bersisa 2 dan f(x) dibagi dengan ( x + 2) bersisa – 1, tentukan sisanya jika f(x) dibagi ( x – 1 )(x + 2 ).

Tugas 2 kelompok 1. Tentukan hasil bagi dan sisa pembagiannya : a. (2 x 4 – 3 x 3 + 5 x – 2) : (x 2 – x – 2 ) b. (3 x 8 – 4 x 4 – 5 ) : (x 2 – 3 x – 4 ) 2. Jika P(x) dibagi oleh (x– 2) dan (x +3) masing-masing bersisa 5 dan - 10. tentukan sisanya jika P(x) dibagi (x 2 + x – 6 ). 3. Tentukan nilai p agar 4 x 2 – 12 x + p habis dibagi 2 x – 1. 4. Tentukan nilai p dan q jika sukubanyak P(x) = 2 x 3 – px 2 + 4 x + q habis dibagi 2 x 2 + x – 1. 5. Sukubanyak P(x) habis dibagi x + 1 dan dibagi x 2 – 4 bersisa 4 x + 16. tentukan sisa pembagian P(x) oleh (x 2 – 4)(x + 1).

D. Teorema Faktor Jika f(x) adalah sukubanyak; (x – k) merupakan faktor dari P(x) jika dan hanya jika P(k) = 0 Artinya: 1. Jika (x – k) merupakan faktor, maka nilai P(k) = 0 sebaliknya, 2. jika P(k) = 0 maka (x – k) merupakan faktor

Ex. 9 Tunjukan (x + 1) faktor dari x 3 + 4 x 2 + 2 x – 1 Jawab: (x + 1) faktornya, berarti P(-1) = 0 P(-1) = (-1)3 + 4(-1)2 + 2(-1) – 1 = -1 + 4 – 2 – 1 = 0 Jadi, (x + 1) adalah faktornya. Ex. 10 Tentukan faktor-faktor dari P(x) = 2 x 3 – x 2 – 7 x + 6 Jawab: Misalkan faktornya (x – k), maka nilai k yang mungkin adalah pembagi bulat dari 6, yaitu

pembagi bulat dari 6 ada 8 yaitu: ± 1, ± 2, ± 3, dan ± 6. Nilai-nilai k itu kita substitusikan ke P(x), misalnya k = 1 diperoleh: P(1) = 2. 13 – 1. 12 – 7. 1 + 6 =2– 1– 7+6 =0 Oleh karena P(1) = 0, maka (x – 1) adalah satu faktor dari P(x) = 2 x 3 – x 2 -7 x + 6 Untuk mencari faktor yang lain, kita tentukan hasil bagi P(x) oleh (x – 1) dengan pembagian horner:

Koefisien sukubanyak P(x) = 2 x 3 – x 2 – 7 x + 6 adalah 2 -1 -7 6 k=1 -6 2 1 -6 + 0 Koefisien hasil bagi Hasil baginya: H(x) = 2 x 2 + x - 6 Karena hasil baginya adalah H(x) = 2 x 2 + x – 6 = (2 x – 3)(x + 2) dengan demikian 2 x 3 – x – 7 x + 6 = (x – 1)(2 x 2 + x – 6) 2 x 3 – x – 7 x + 6 = (x – 1)(2 x – 3)(x + 2) Jadi faktor-faktornya adalah (x – 1), (2 x – 3 ) dan (x + 2)

E. Akar-akar Rasional Persamaan Sukubanyak Salah satu penggunaan teorema faktor adalah mencari akar sebuah persamaan sukubanyak, karena ada hubungan antara faktor dengan akar-akar persamaan sukubanyak Jika P(x) adalah sukubanyak; (x – k) merupakan faktor dari P(x) jika dan hanya jika k akar dari persamaan P(k) = 0 k disebut akar atau nilai nol dari persamaan sukubanyak: P(x) = 0 Teorema Akar-akar Rasional Jika P(x) =anxn + an-1 xn-1 + …+ a 1 x + ao dan (x – k) merupakan faktor dari P(x) maka

Ex. 11 Tunjukan -3 adalah satu akar dari x 3 – 7 x + 6. Kemudian tentukan akar-akar yang lain. Jawab: Untuk menunjukan -3 akar dari P(x), cukup kita tunjukan bahwa P(-3) = 0 P(x) = x 3 – 7 x + 6. P(-3) = (-3)3 – 7(-3) + 6 = -27 + 21 + 6 =0 Oleh karena P(-3) = 0, maka -3 adalah akar dari Persamaan P(x) = x 3 – 7 x + 6 = 0

Untuk menentukan akar-akar yang lain, kita tentukan terlebih dahulu hasil bagi P(x) = x 3 – 7 x + 6 dengan x + 3 dengan pembagian Horner sebagai berikut P(x) = x 3 – 7 x + 6 berarti koefisien P(x) adalah 1 0 -7 6 k = -3 9 -6 -3 1 -3 2 + 0 Koefisien hasil bagi Hasil baginya: H(x) = x 2 – 3 x + 2 =(x – 1)(x – 2)

Hasil baginya: H(x) = x 2 – 3 x + 2 = (x – 1)(x – 2) sehingga persamaan sukubanyak tsb dapat ditulis menjadi (x + 3)(x – 1)(x – 2) = 0. Jadi akar-akar yang lain adalah x = 1 dan x = 2 Ex. 12 Tentukan akar-akar rasional dari persamaan x 4 – 3 x 2 + 2 = 0. Karena persamaan sukubanyak berderajat 4, maka akar rasionalnya paling banyak ada 4 yaitu faktor-faktor bulat dari 2. Faktor-faktor bulat dari 2 adalah 1, -1, 2 dan -2

Misal : an xn +an-1 xn-1 +. . + a 1 x + a 0 = 0, dengan a 0 ≠ 0 i). Jika sebuah bilangan rasional, Dimana b = faktor bulat dari a 0 c = faktor bulat dari an Algoritma penentuan akar rasional polinom P(x) = 0 ii). 1. Selidiki apakah jumlah koefisien P(x) = 0 @ Jika ya, maka x = 1 merupakan akar dari P(x) = 0 ? @ Jika tidak, lakukan langkah berikut. 2. Periksa apakah jumlah koefisien variabel berpangkat genap sama dengan jumlah koefisien berpangkat ganjil. @ Jika ya, maka x = -1 merupakan akar dari P(x) = 0 @ Jika tidak, lakukan langkah berikut. 3. Tentukan faktor-faktor dari nilai nutlak a 0, lakukan dengan cara coba-coba.

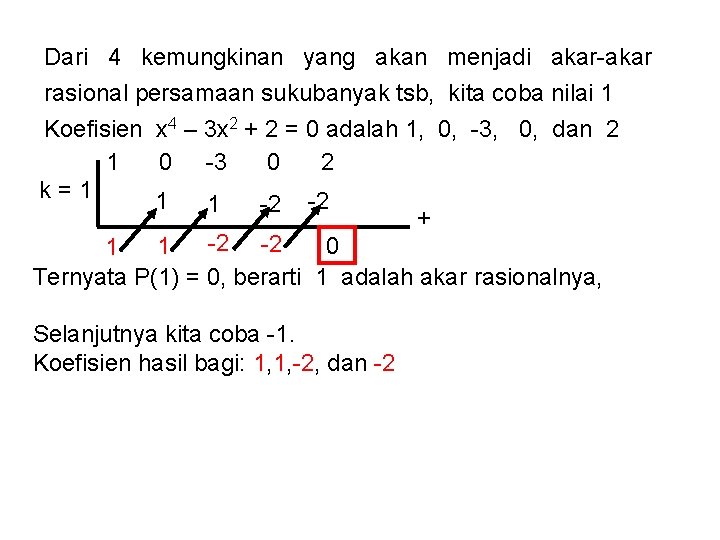
Dari 4 kemungkinan yang akan menjadi akar-akar rasional persamaan sukubanyak tsb, kita coba nilai 1 Koefisien x 4 – 3 x 2 + 2 = 0 adalah 1, 0, -3, 0, dan 2 1 0 -3 0 2 k=1 1 1 -2 -2 + -2 -2 1 0 1 Ternyata P(1) = 0, berarti 1 adalah akar rasionalnya, Selanjutnya kita coba -1. Koefisien hasil bagi: 1, 1, -2, dan -2

1 k = -1 1 1 -2 -2 -1 0 2 0 -2 0 + Ternyata P(-1) = 0, berarti -1 adalah akar rasionalnya, Sehingga: (x – 1)(x + 1)(x 2 – 2) = 0 Untuk : (x 2 – 2) dapat difaktorkan lagi menjadi (x - √ 2)(x + √ 2) = 0 Berarti akar yang lain: √ 2 dan -√ 2, tapi bukan bilangan rasional. Jadi akar-akar rasionalnya hanya ada 2 yaitu 1 dan -1.

(x – 1)(x + 1)(x 2 – 2) = 0 (x 2 – 2) difaktorkan lagi menjadi (x - √ 2)(x + √ 2) = 0 Berarti akar yang lain: √ 2 dan -√ 2, tapi bukan bilangan rasional. Jadi akar-akar rasionalnya hanya ada 2 yaitu 1 dan -1.

Jumlah dan Hasil Kali Akar-akar Persamaan Sukubanyak

Jika akar-akar Persamaan Sukubanyak: ax 3 + bx 2 + cx + d = 0 adalah x 1, x 2, dan x 3 maka x 1 + x 2 + x 3 = x 1. x 2 + x 1. x 3 + x 2. x 3 = x 1. x 2. x 3 =

Contoh 1: Jumlah akar-akar persamaan x 3 – 3 x 2 + 2 = 0 adalah…. Jawab: a = 1, b = -3, c = 0, d = 2 x 1 + x 2 + x 3 = =3 =

Contoh 2: Hasilkali akar-akar persamaan 2 x 3 – x 2 + 5 x – 8 = 0 adalah…. Jawab: a = 2, b = -1, c = 5, d = -8 x 1. x 2. x 3 = = =4

Contoh 3: Salah satu akar persamaan x 3 + px 2 – 3 x – 10 = 0 adalah -2 Jumlah akar-akar persamaan tersebut adalah….

Jawab: -2 adalah akar persamaan x 3 + px 2 – 3 x - 10 = 0 → -2 memenuhi persamaan tsb. sehingga: (-2)3 + p(-2)2 – 3(-2) - 10 = 0 -8 + 4 p + 6 – 10 = 0

-8 + 4 p + 6 – 10 = 0 4 p – 12 = 0 4 p = 12 p = 3 Persamaan tersebut: x 3 + 3 x 2 – 3 x – 10 = 0 Jumlah akar-akarnya: x 1 + x 2 + x 3 = = = -3

Contoh 4: Akar-akar persamaan x 3 – 4 x 2 + x – 4 = 0 adalah x 1, x 2, dan x 3. Nilai x 12 + x 22 + x 32 =….

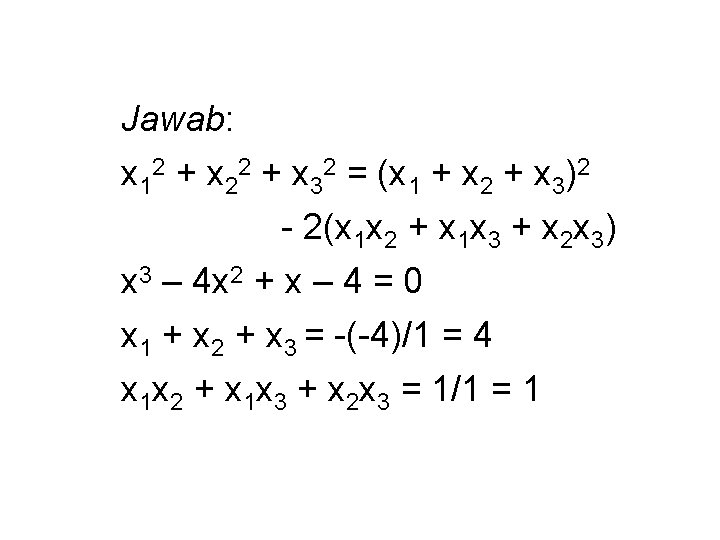
Jawab: x 12 + x 22 + x 32 = (x 1 + x 2 + x 3)2 - 2(x 1 x 2 + x 1 x 3 + x 2 x 3) x 3 – 4 x 2 + x – 4 = 0 x 1 + x 2 + x 3 = -(-4)/1 = 4 x 1 x 2 + x 1 x 3 + x 2 x 3 = 1/1 = 1

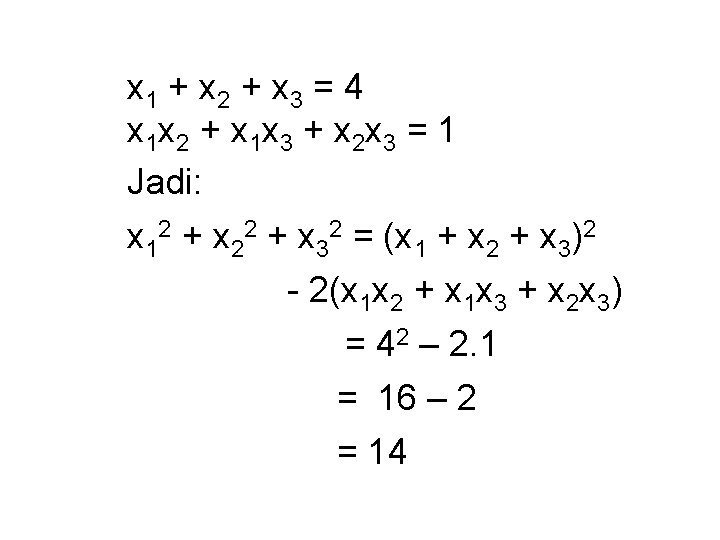
x 1 + x 2 + x 3 = 4 x 1 x 2 + x 1 x 3 + x 2 x 3 = 1 Jadi: x 12 + x 22 + x 32 = (x 1 + x 2 + x 3)2 - 2(x 1 x 2 + x 1 x 3 + x 2 x 3) = 42 – 2. 1 = 16 – 2 = 14