Poligoni inscritti in una circonferenza DEFINIZIONE Un poligono

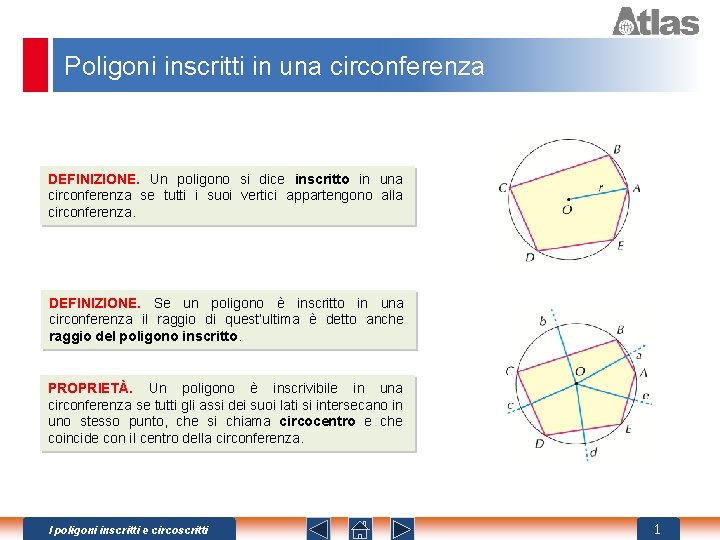
Poligoni inscritti in una circonferenza DEFINIZIONE. Un poligono si dice inscritto in una circonferenza se tutti i suoi vertici appartengono alla circonferenza. DEFINIZIONE. Se un poligono è inscritto in una circonferenza il raggio di quest’ultima è detto anche raggio del poligono inscritto. PROPRIETÀ. Un poligono è inscrivibile in una circonferenza se tutti gli assi dei suoi lati si intersecano in uno stesso punto, che si chiama circocentro e che coincide con il centro della circonferenza. I poligoni inscritti e circoscritti 1

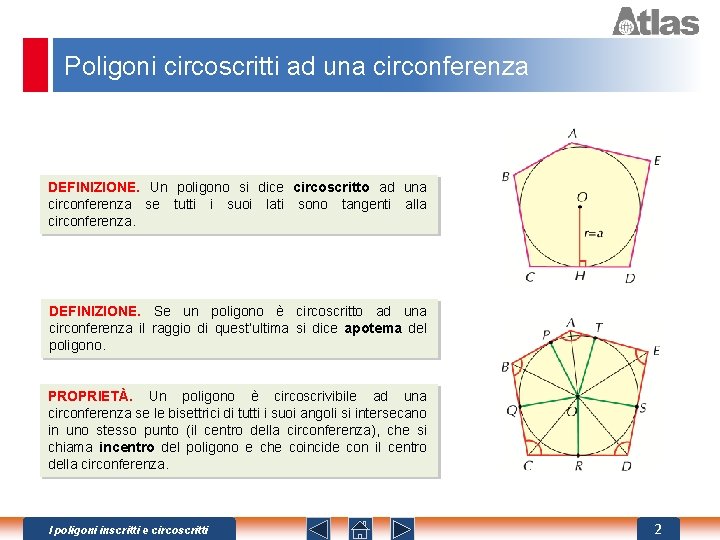
Poligoni circoscritti ad una circonferenza DEFINIZIONE. Un poligono si dice circoscritto ad una circonferenza se tutti i suoi lati sono tangenti alla circonferenza. DEFINIZIONE. Se un poligono è circoscritto ad una circonferenza il raggio di quest’ultima si dice apotema del poligono. PROPRIETÀ. Un poligono è circoscrivibile ad una circonferenza se le bisettrici di tutti i suoi angoli si intersecano in uno stesso punto (il centro della circonferenza), che si chiama incentro del poligono e che coincide con il centro della circonferenza. I poligoni inscritti e circoscritti 2

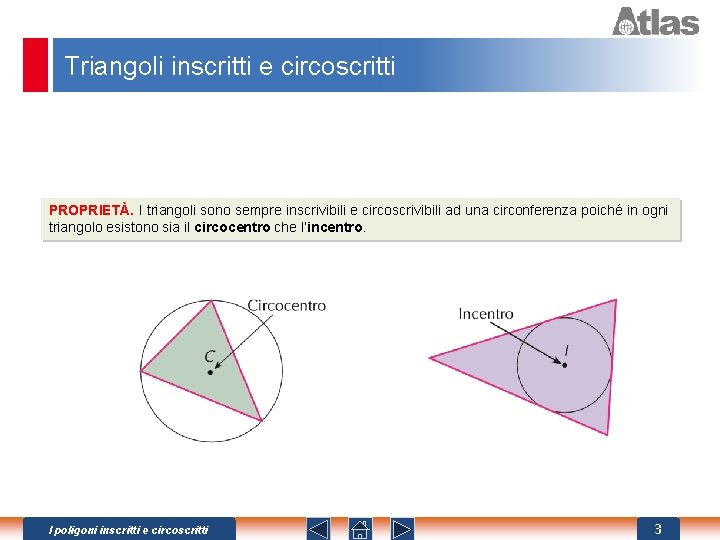
Triangoli inscritti e circoscritti PROPRIETÀ. I triangoli sono sempre inscrivibili e circoscrivibili ad una circonferenza poiché in ogni triangolo esistono sia il circocentro che l’incentro. I poligoni inscritti e circoscritti 3

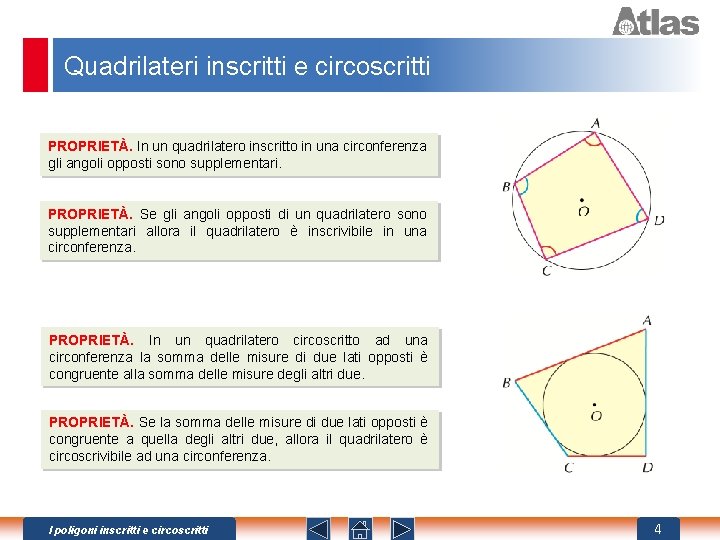
Quadrilateri inscritti e circoscritti PROPRIETÀ. In un quadrilatero inscritto in una circonferenza gli angoli opposti sono supplementari. PROPRIETÀ. Se gli angoli opposti di un quadrilatero sono supplementari allora il quadrilatero è inscrivibile in una circonferenza. PROPRIETÀ. In un quadrilatero circoscritto ad una circonferenza la somma delle misure di due lati opposti è congruente alla somma delle misure degli altri due. PROPRIETÀ. Se la somma delle misure di due lati opposti è congruente a quella degli altri due, allora il quadrilatero è circoscrivibile ad una circonferenza. I poligoni inscritti e circoscritti 4

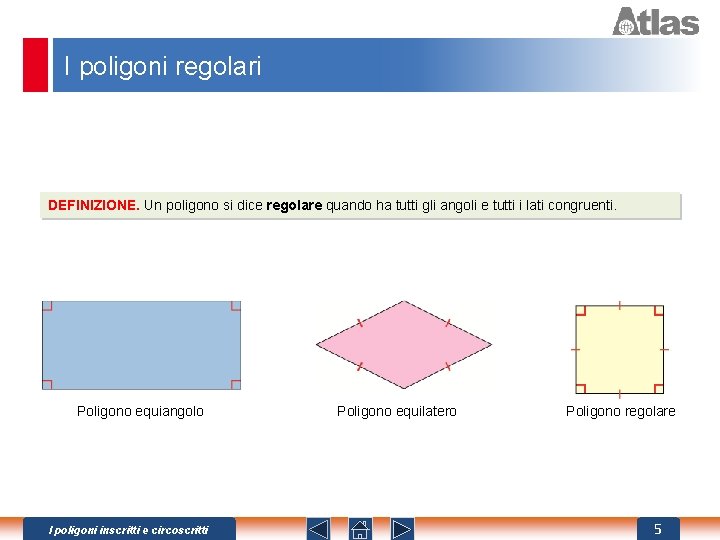
I poligoni regolari DEFINIZIONE. Un poligono si dice regolare quando ha tutti gli angoli e tutti i lati congruenti. Poligono equiangolo I poligoni inscritti e circoscritti Poligono equilatero Poligono regolare 5

I poligoni regolari PROPRIETÀ. Un poligono regolare è sempre inscrivibile e circoscrivibile ad una circonferenza. PROPRIETÀ. Il centro O del poligono regolare è il centro sia della circonferenza circoscritta (circocentro) che della circonferenza inscritta (incentro). PROPRIETÀ. Il raggio della circonferenza circoscritta è il raggio del poligono; il raggio della circonferenza inscritta è l’apotema del poligono. I poligoni inscritti e circoscritti 6

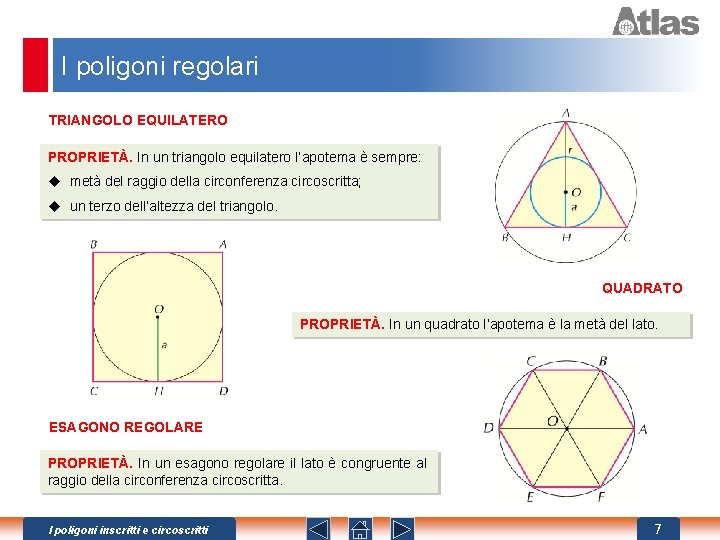
I poligoni regolari TRIANGOLO EQUILATERO PROPRIETÀ. In un triangolo equilatero l’apotema è sempre: u metà del raggio della circonferenza circoscritta; u un terzo dell’altezza del triangolo. QUADRATO PROPRIETÀ. In un quadrato l’apotema è la metà del lato. ESAGONO REGOLARE PROPRIETÀ. In un esagono regolare il lato è congruente al raggio della circonferenza circoscritta. I poligoni inscritti e circoscritti 7

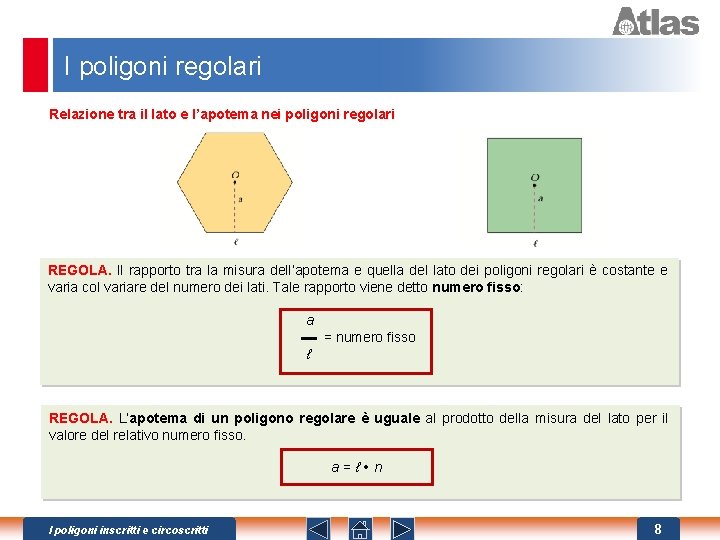
I poligoni regolari Relazione tra il lato e l’apotema nei poligoni regolari REGOLA. Il rapporto tra la misura dell’apotema e quella del lato dei poligoni regolari è costante e varia col variare del numero dei lati. Tale rapporto viene detto numero fisso: a = numero fisso ℓ REGOLA. L’apotema di un poligono regolare è uguale al prodotto della misura del lato per il valore del relativo numero fisso. a=ℓ n I poligoni inscritti e circoscritti 8