Poligoni e triangoli SPEZZATA Si chiama spezzata una

Poligoni e triangoli

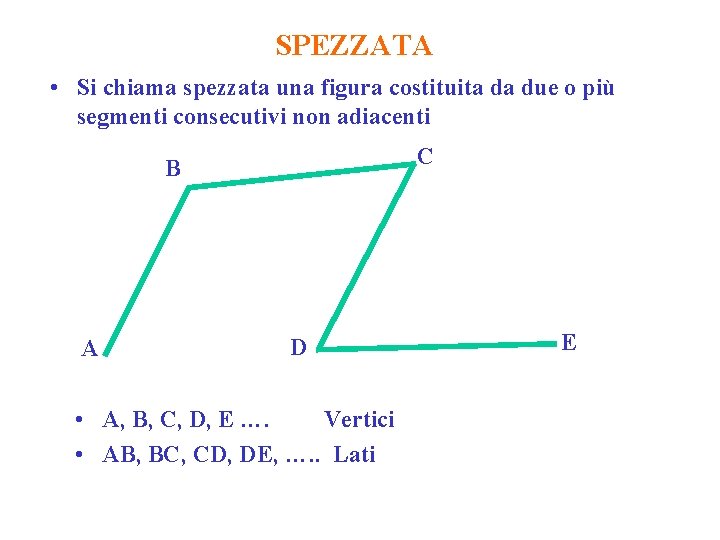
SPEZZATA • Si chiama spezzata una figura costituita da due o più segmenti consecutivi non adiacenti C B A D • A, B, C, D, E …. Vertici • AB, BC, CD, DE, …. . Lati E

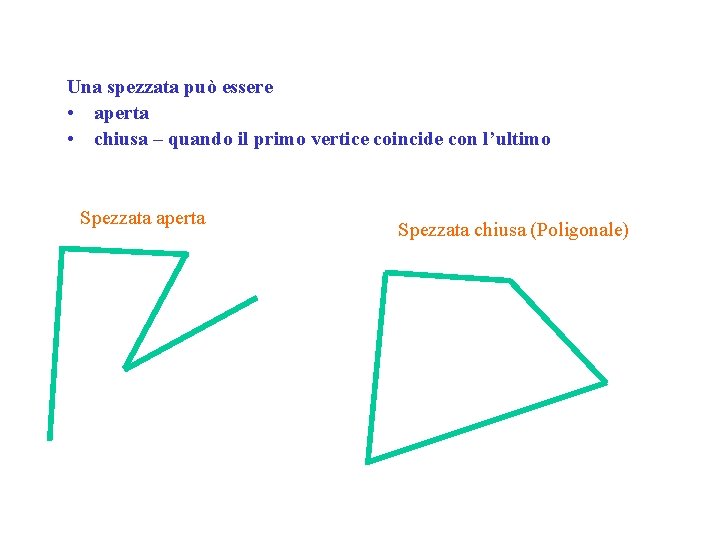
Una spezzata può essere • aperta • chiusa – quando il primo vertice coincide con l’ultimo Spezzata aperta Spezzata chiusa (Poligonale)

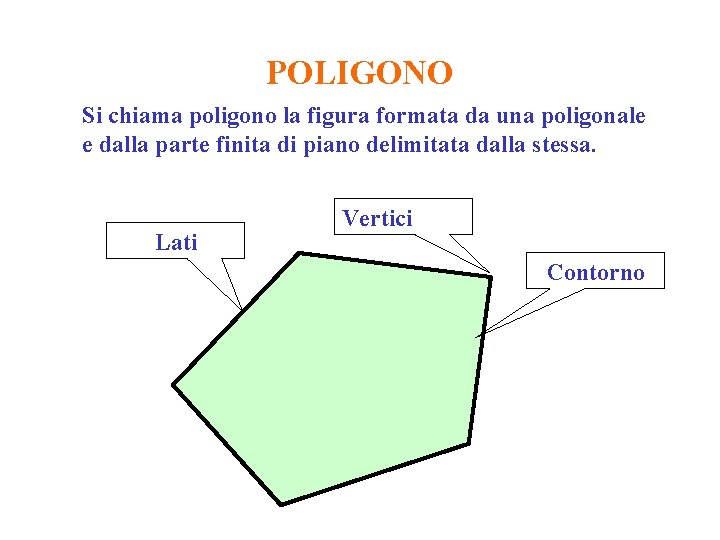
POLIGONO Si chiama poligono la figura formata da una poligonale e dalla parte finita di piano delimitata dalla stessa. Lati Vertici Contorno

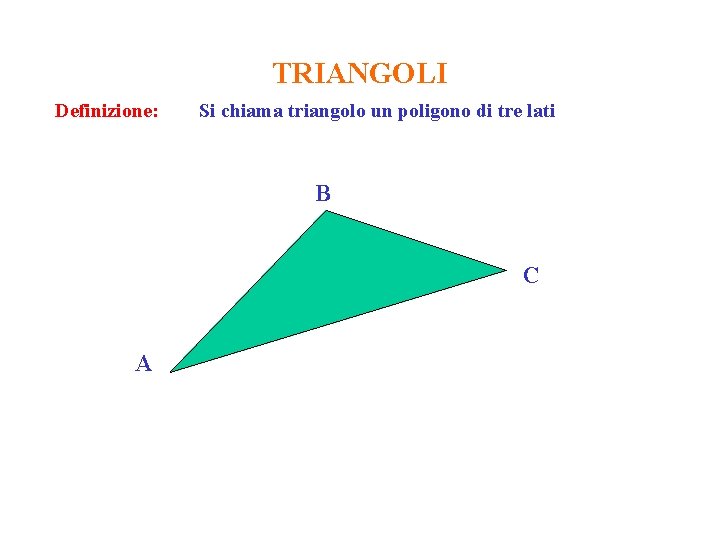
TRIANGOLI Definizione: Si chiama triangolo un poligono di tre lati B C A

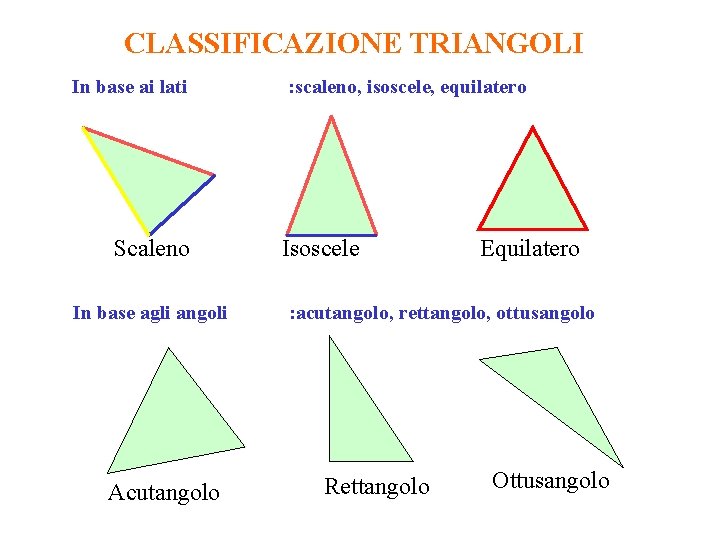
CLASSIFICAZIONE TRIANGOLI In base ai lati Scaleno In base agli angoli Acutangolo : scaleno, isoscele, equilatero Isoscele Equilatero : acutangolo, rettangolo, ottusangolo Rettangolo Ottusangolo

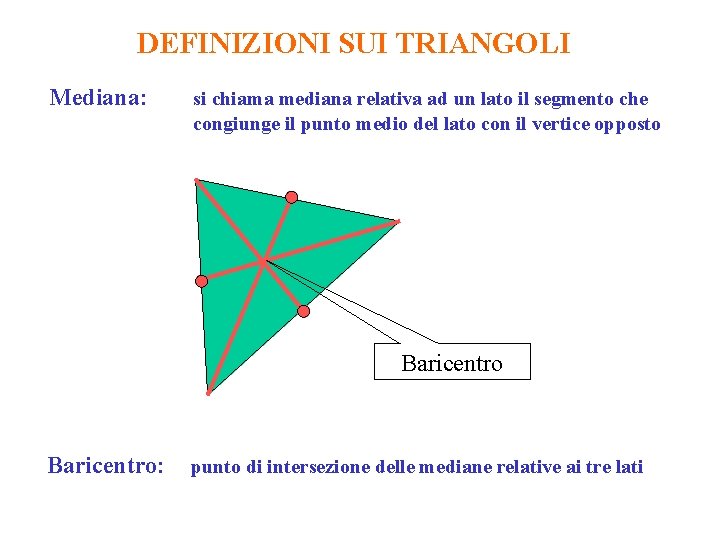
DEFINIZIONI SUI TRIANGOLI Mediana: si chiama mediana relativa ad un lato il segmento che congiunge il punto medio del lato con il vertice opposto Baricentro: punto di intersezione delle mediane relative ai tre lati

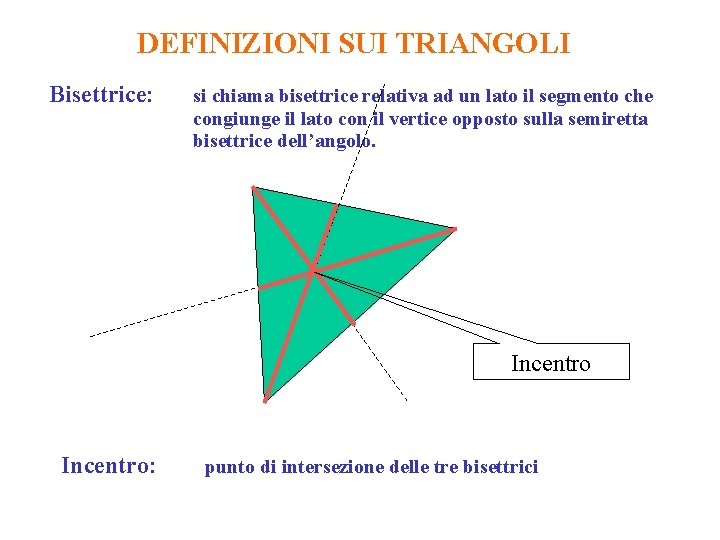
DEFINIZIONI SUI TRIANGOLI Bisettrice: si chiama bisettrice relativa ad un lato il segmento che congiunge il lato con il vertice opposto sulla semiretta bisettrice dell’angolo. Incentro: punto di intersezione delle tre bisettrici

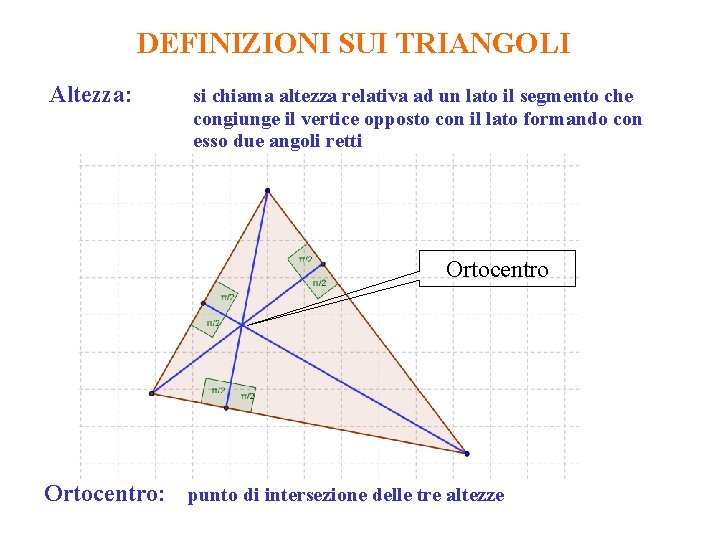
DEFINIZIONI SUI TRIANGOLI Altezza: si chiama altezza relativa ad un lato il segmento che congiunge il vertice opposto con il lato formando con esso due angoli retti Ortocentro: punto di intersezione delle tre altezze

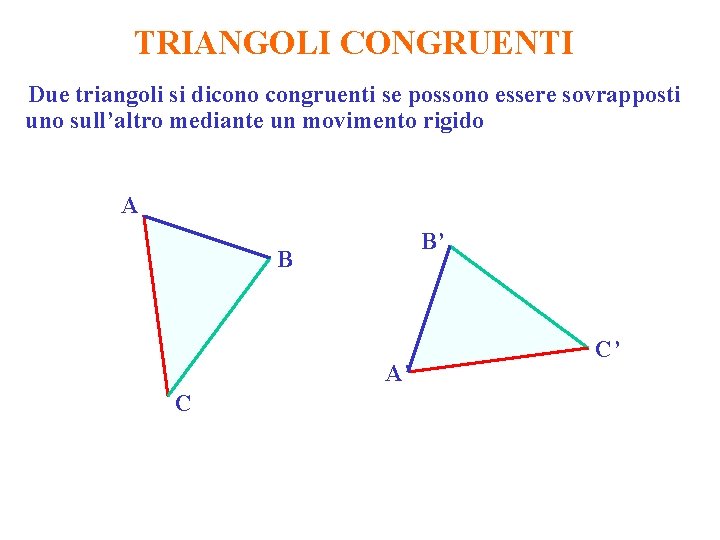
TRIANGOLI CONGRUENTI Due triangoli si dicono congruenti se possono essere sovrapposti uno sull’altro mediante un movimento rigido A B’ B A’ C C’

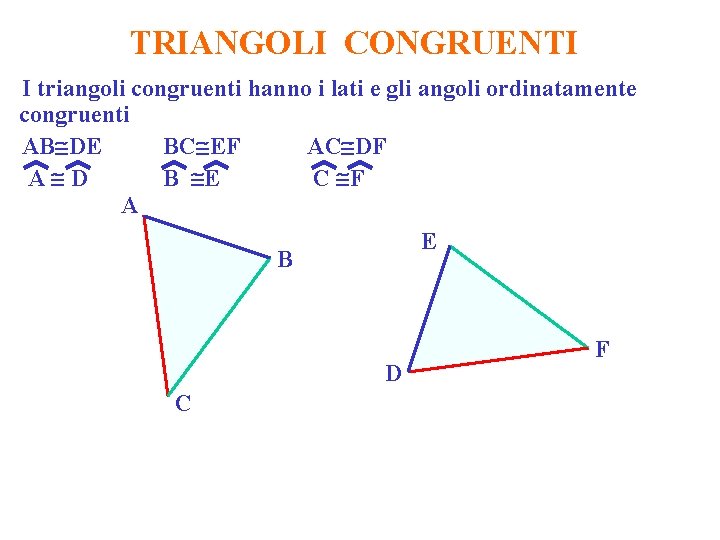
TRIANGOLI CONGRUENTI I triangoli congruenti hanno i lati e gli angoli ordinatamente congruenti AB DE BC EF AC DF A D B E C F A E B D C F

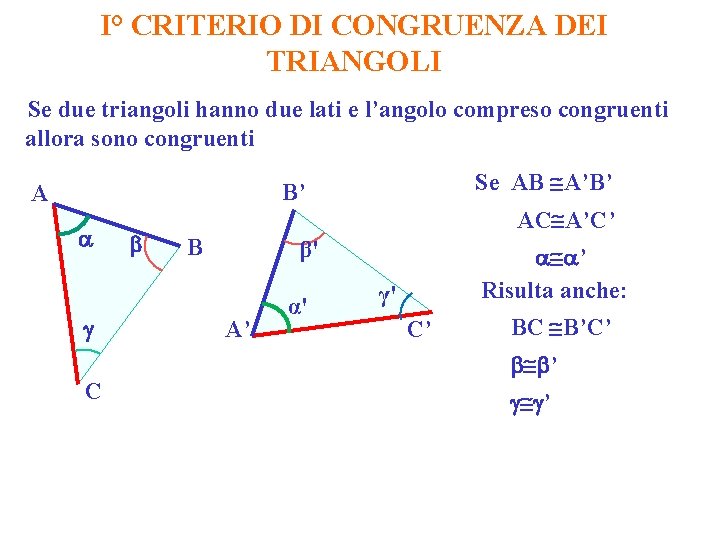
I° CRITERIO DI CONGRUENZA DEI TRIANGOLI Se due triangoli hanno due lati e l’angolo compreso congruenti allora sono congruenti Se AB A’B’ B’ A C AC A’C’ B β' A’ α' ’ Risulta anche: γ' C’ BC B’C’ ’ ’

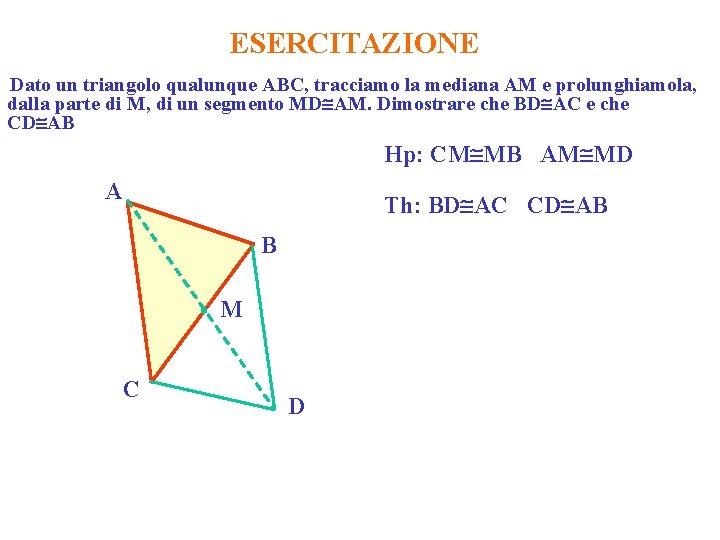
ESERCITAZIONE Dato un triangolo qualunque ABC, tracciamo la mediana AM e prolunghiamola, dalla parte di M, di un segmento MD AM. Dimostrare che BD AC e che CD AB Hp: CM MB AM MD A Th: BD AC CD AB B M C D

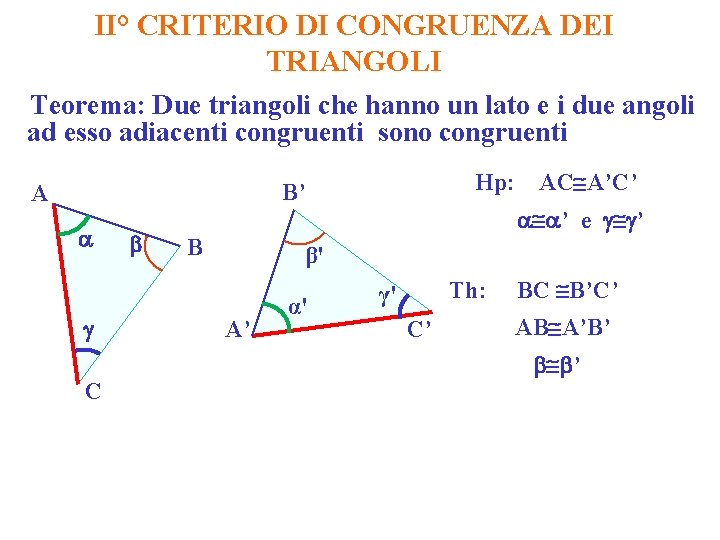
II° CRITERIO DI CONGRUENZA DEI TRIANGOLI Teorema: Due triangoli che hanno un lato e i due angoli ad esso adiacenti congruenti sono congruenti Hp: B’ A C B AC A’C’ ’ e ’ β' A’ α' Th: γ' C’ BC B’C’ AB A’B’ ’

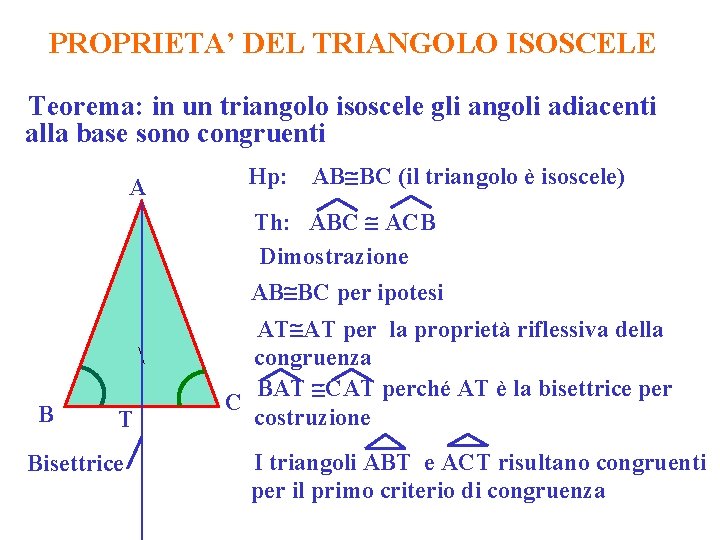
PROPRIETA’ DEL TRIANGOLO ISOSCELE Teorema: in un triangolo isoscele gli angoli adiacenti alla base sono congruenti A Hp: AB BC (il triangolo è isoscele) Th: ABC ACB Dimostrazione AB BC per ipotesi B T Bisettrice AT AT per la proprietà riflessiva della congruenza BAT CAT perché AT è la bisettrice per C costruzione I triangoli ABT e ACT risultano congruenti per il primo criterio di congruenza

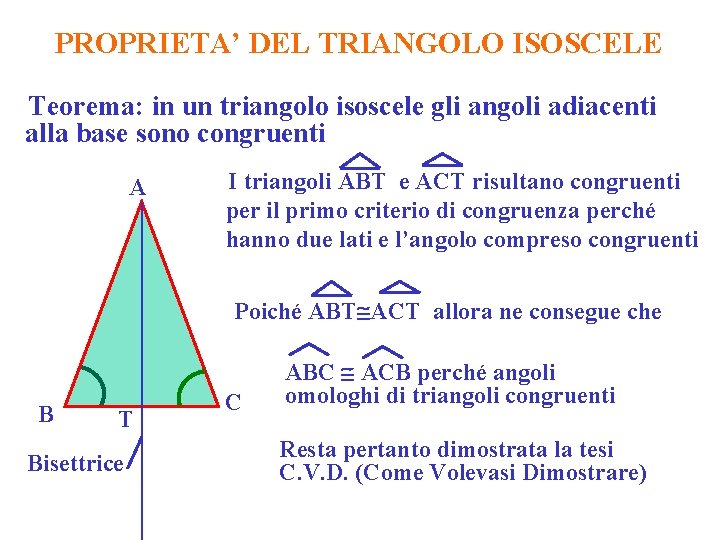
PROPRIETA’ DEL TRIANGOLO ISOSCELE Teorema: in un triangolo isoscele gli angoli adiacenti alla base sono congruenti A I triangoli ABT e ACT risultano congruenti per il primo criterio di congruenza perché hanno due lati e l’angolo compreso congruenti Poiché ABT ACT allora ne consegue che B T Bisettrice C ABC ACB perché angoli omologhi di triangoli congruenti Resta pertanto dimostrata la tesi C. V. D. (Come Volevasi Dimostrare)

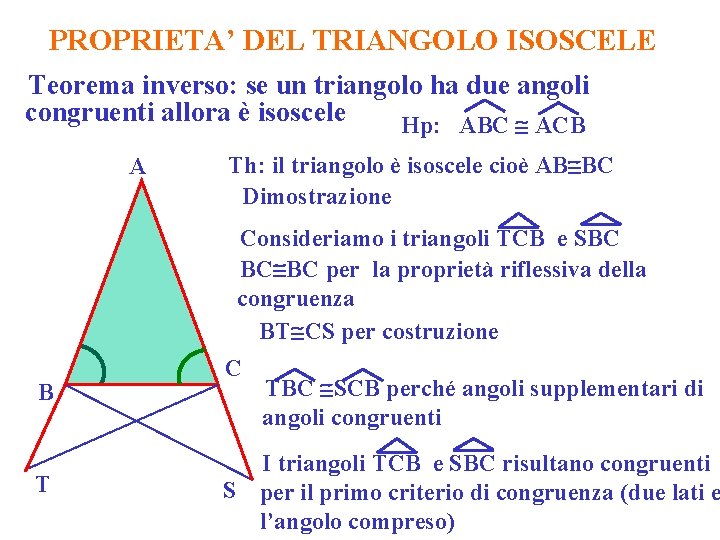
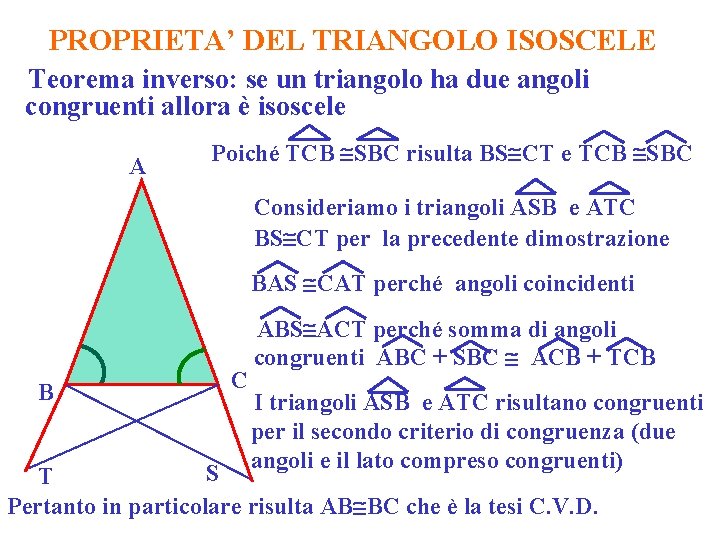
PROPRIETA’ DEL TRIANGOLO ISOSCELE Teorema inverso: se un triangolo ha due angoli congruenti allora è isoscele Hp: ABC ACB A Th: il triangolo è isoscele cioè AB BC Dimostrazione Consideriamo i triangoli TCB e SBC BC BC per la proprietà riflessiva della congruenza BT CS per costruzione B T C TBC SCB perché angoli supplementari di angoli congruenti I triangoli TCB e SBC risultano congruenti S per il primo criterio di congruenza (due lati e l’angolo compreso)

PROPRIETA’ DEL TRIANGOLO ISOSCELE Teorema inverso: se un triangolo ha due angoli congruenti allora è isoscele A Poiché TCB SBC risulta BS CT e TCB SBC Consideriamo i triangoli ASB e ATC BS CT per la precedente dimostrazione BAS CAT perché angoli coincidenti B C ABS ACT perché somma di angoli congruenti ABC + SBC ACB + TCB I triangoli ASB e ATC risultano congruenti per il secondo criterio di congruenza (due angoli e il lato compreso congruenti) S T Pertanto in particolare risulta AB BC che è la tesi C. V. D.

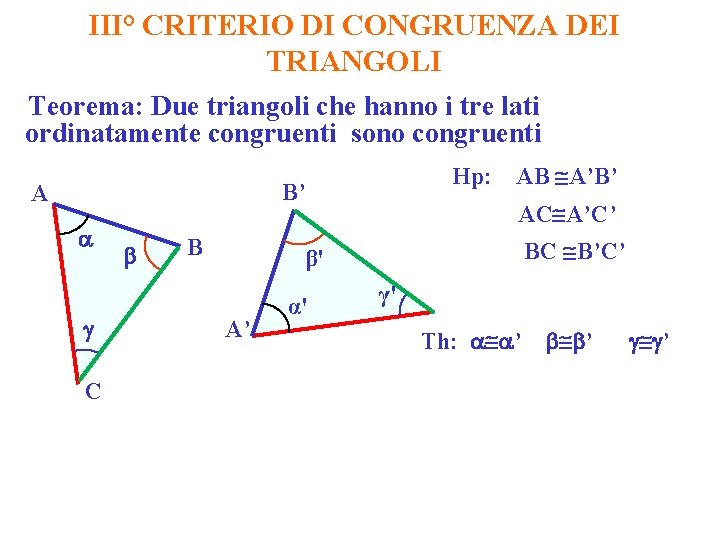
III° CRITERIO DI CONGRUENZA DEI TRIANGOLI Teorema: Due triangoli che hanno i tre lati ordinatamente congruenti sono congruenti Hp: B’ A C B AB A’B’ AC A’C’ BC B’C’ β' A’ α' γ' Th: ’ ’ ’