POLIEDRI RADILI Marta Mirkov Milica Bai Katarina Stefanovi

POLIEDRI RADILI : Marta Mirkov, Milica Bačić, Katarina Stefanović, Jelena Zlatanović, Mihailo Golović i Dimitrije Čabarkapa

POLIEDARSKA POVRŠ • Skup površi mnogouglova, takvih da je svaka stranica svakog mnogougla ujedno i stranica još samo jednog mnogougla, obrazuju zatvorenu površ koja se naziva poliedarska površ. Deo geometrijskog prostora koji ograničava zatvorena poliedarska površ je unutrašnjost poliedarske površi • Poliedarska površ sa svojom unutrašnjošću čini poliedar • Svaka duž koja spaja dva temena poliedra, a ne pripada nijednoj strani poliedra predstavlja dijagonalu poliedra • Svaka ravan koju određuju tri temena poliedra i ne sadrži nijednu stranu poliedra predstavlja dijagonalnu ravan poliedra

DUALNI POLIEDDRI U geometriji poliedri se posmatraju u parovima. Svakom poliedru odgovara dualni poliedar koji nastaje metamorfozom datog poliedra u kojoj : • svakom temenu polaznog poliedra odgovara strana novog poliedra • svakoj strani polaznog poliedra odgovara teme novog poliedra • svakoj ivici polaznog poliedra odgovara ivica novog poliedra

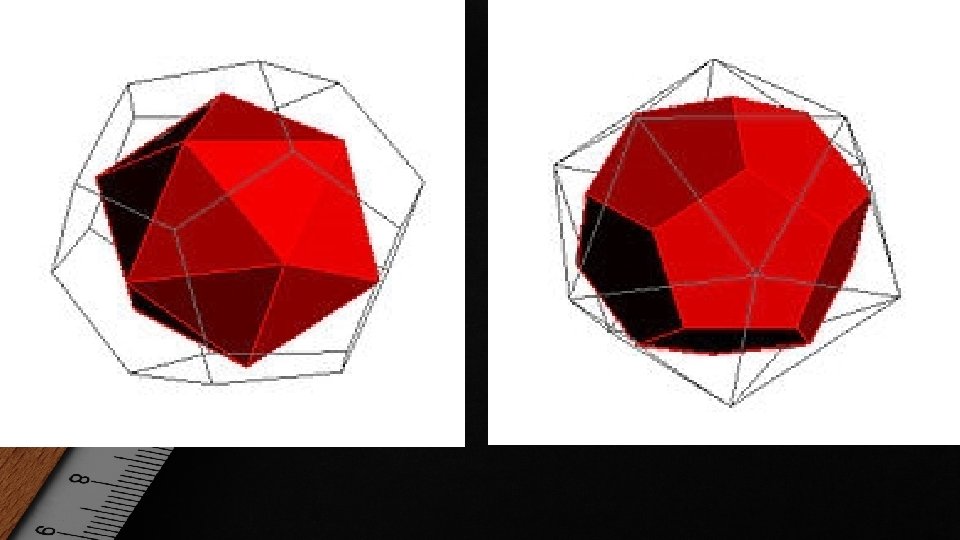
POLIEDRI KONVEKSNI KONKAVNI • Poliedar je konveksan ukoliko svaka duž koja spaja njegove dve proizvoljne tačke pripada tom poliedru, u suprotnom slučaju poliedar je nekonveksan odnosno konkavan • Konveksan poliedar leži samo sa jedne strane ravni svake svoje strane

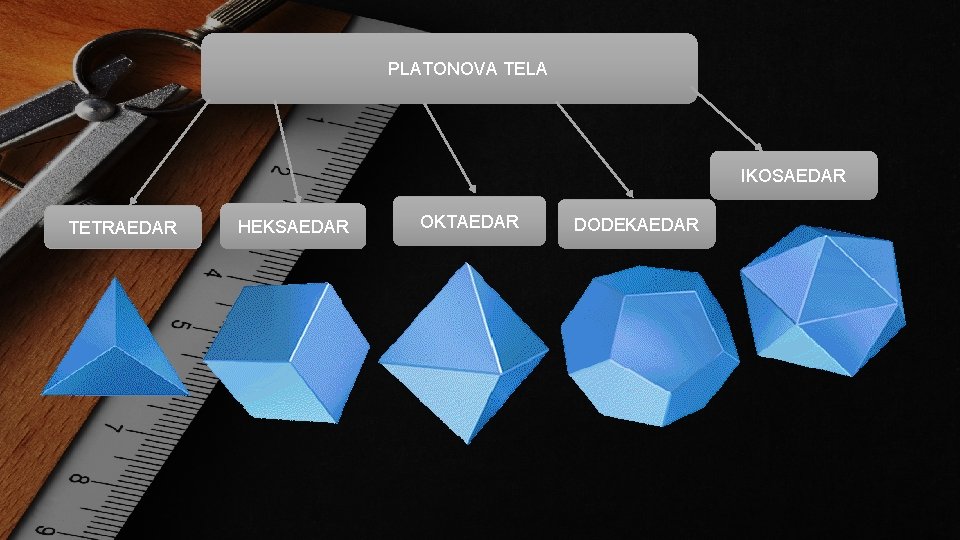
PLATONOVA TELA IKOSAEDAR TETRAEDAR HEKSAEDAR OKTAEDAR DODEKAEDAR

• Platon • Euklid • Johan Kepler • Leonardo Ojler

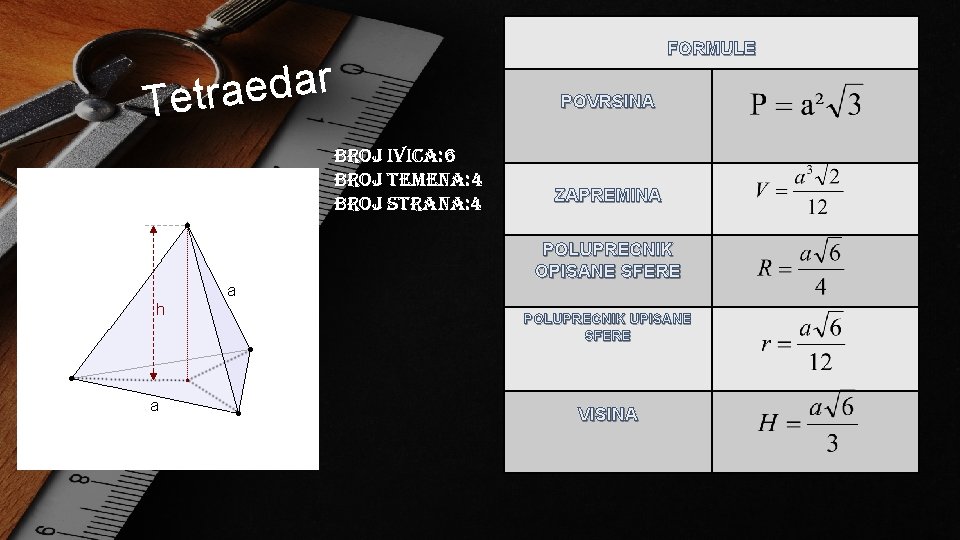
FORMULE r a d e a Tetr POVRSINA Broj ivica: 6 Broj temena: 4 Broj strana: 4 ZAPREMINA POLUPRECNIK OPISANE SFERE POLUPRECNIK UPISANE SFERE VISINA

r a d e Heksa Broj ivica: 12 Broj temena: 8 Broj strana: 6 FORMULE POVRSINA ZAPREMINA POLUPRECNIK OPISANE SFERE POLUPRECNIK UPISANE SFERE Mala dijagonala Velika dijagonala

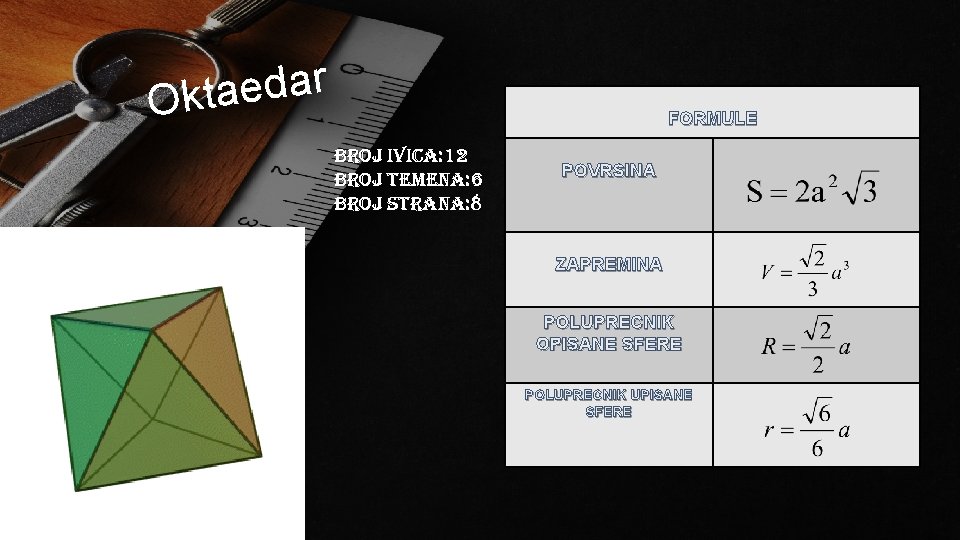
r a d e a Okt FORMULE Broj ivica: 12 Broj temena: 6 Broj strana: 8 POVRSINA ZAPREMINA POLUPRECNIK OPISANE SFERE POLUPRECNIK UPISANE SFERE

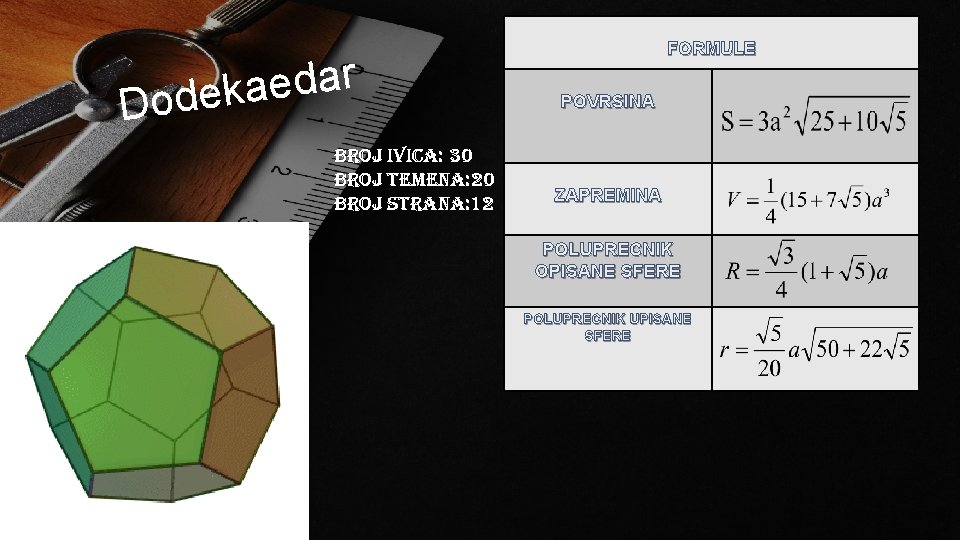
r a d e a k e d o D Broj ivica: 30 Broj temena: 20 Broj strana: 12 FORMULE POVRSINA ZAPREMINA POLUPRECNIK OPISANE SFERE POLUPRECNIK UPISANE SFERE

r a d e o Ikos Broj ivica: 30 Broj temena: 12 Broj strana: 20 FORMULE POVRSINA ZAPREMINA POLUPRECNIK OPISANE SFERE POLUPRECNIK UPISANE SFERE

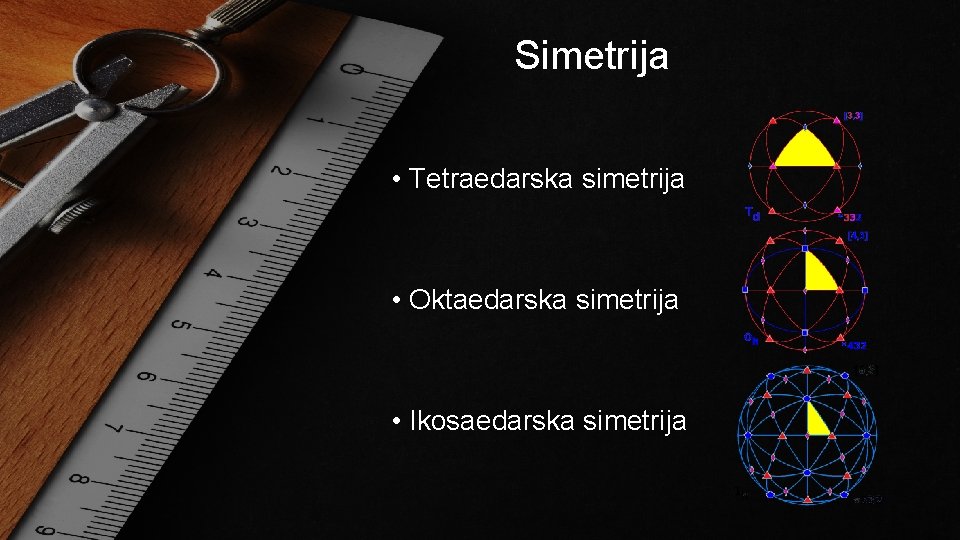
Simetrija • Tetraedarska simetrija • Oktaedarska simetrija • Ikosaedarska simetrija

Izometrija • Translacija • Rotacija • Refleksija • Izvodjenje

Ojlerova teorema • Zbir strana i temena svakog prostog zatvorenog poliedra je za 2 veći od broja ivica istog poliedra. s+t=i+2

HVALA NA PAŽNJI!